
1 图形学概述 overview of computer graphics
- 游戏的画面好不好,看它的
画面亮不亮,越亮越好.
计算机图形学应用于游戏,电影(特效),动画(毛发,粒子),设计 CAD computer aided design (汽车,房子),可视化 visualization (医学成像), 虚拟现实 virtual reality (SwordArt Online), 数字画图 Digital illustration(Photoshop), 模拟 Simulation(沙尘暴, 黑洞), 用户界面 Graphical User Interfaces GUI, 字体 Typography (矢量图)
- CG is awesome!
CG包括:
光栅化Rasterization曲线,网格Curves and Meshes光线追踪Ray Tracing动画/仿真Animation / Simulation
- CG与计算机视觉 computer vision 的区别:
CV需要从图像猜 - 参考书: Fundamentals of Computer Graphics (虎书和其参考章节)
- IDE Integrated Development Envirnment 使用
VS,别做一个Geek,只要genius,不要freak.
2 线性代数 Linear Algabra
简单粗暴的线代入门, A Swift and Brutal Introduction to Linear Algebra.
2.1向量
向量课件
注意一点:
向量默认是列column向量,加T是行row向量
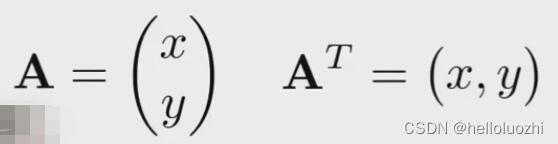
- 单位向量用
hat表示
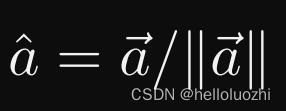
2.1.1 点乘 dot product
向量在另一向量的投影与其乘积. 结果的正负判断两向量是否同方向.
2.1.2 叉乘 cross product
- 叉乘:右手定则判定方向.
- 用处:
判断左右,内外
定义图中右下角坐标系,a叉乘b向外,b叉乘a向内

AB叉乘AP,BC叉乘BP,CA叉乘CP都向外;或者说:‘点P在三条边的左边’
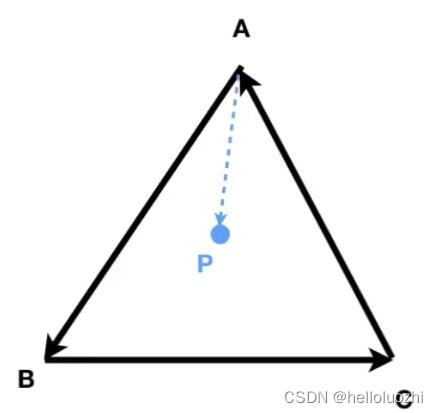
2.2 矩阵 MatriX
m×n表示m行n列!
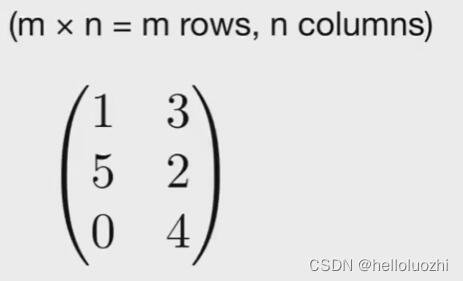
2.2.1 矩阵乘法 Matrix-matrix multiplication
类似GR和微分几何的的张量缩并.
M×N的写法很重要,M表示M行,N表示N列,不能写反了!.比如M×1表示一个长M的列向量!
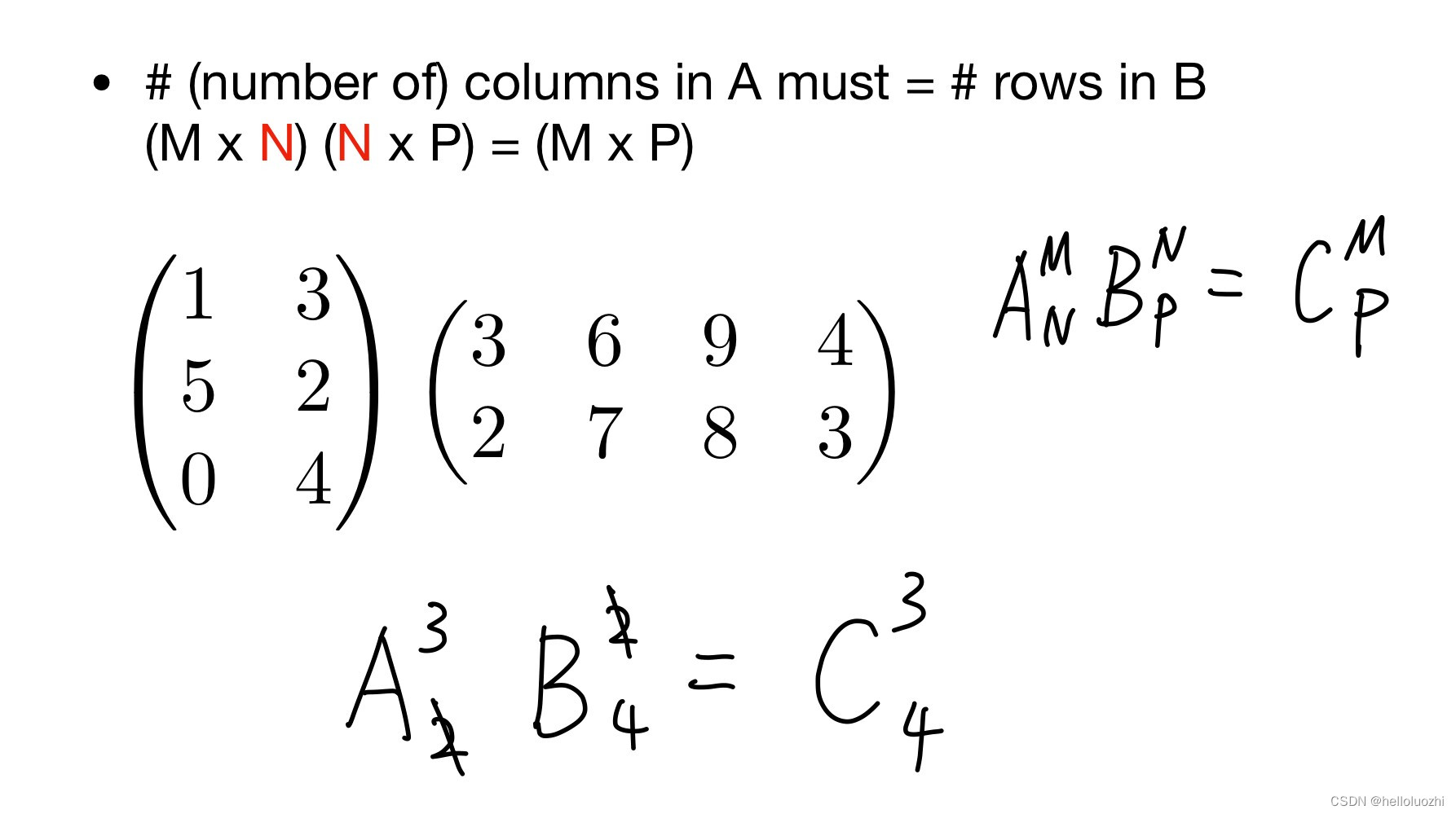
比如右边C的0行0列就是A的0行点乘B的0列,等于9.
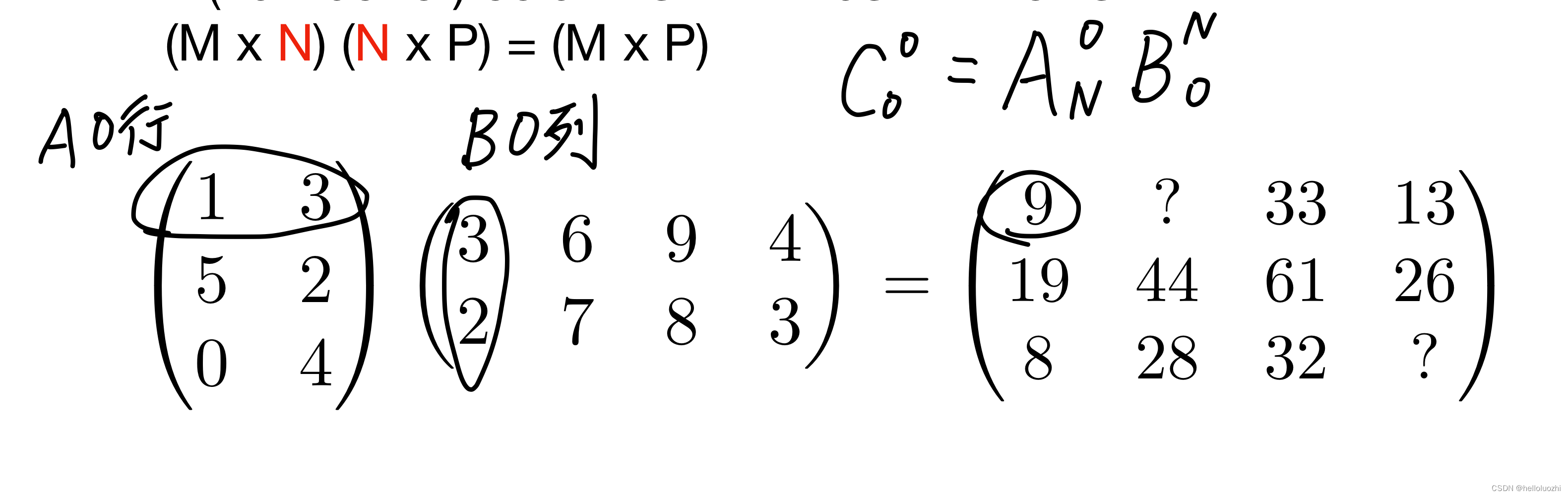
Mathematica的计算,用dot表示乘

- 矩阵乘法不满足交换律(不对易,AB不等于BA)
2.2.2 矩阵乘向量 Matrix-vector multiplication
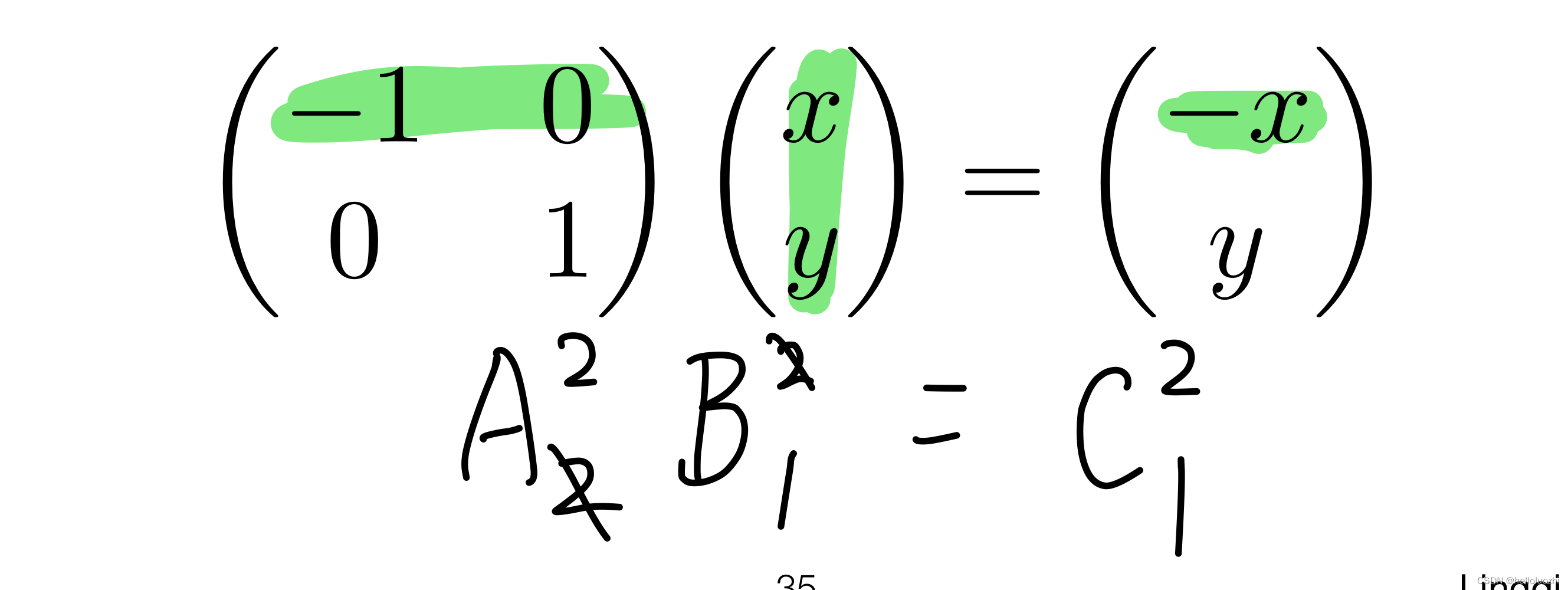
Mathematica复现:

- 其他例子

2.2.3 转置 transpose 和逆 inverse
- 转置

- 逆
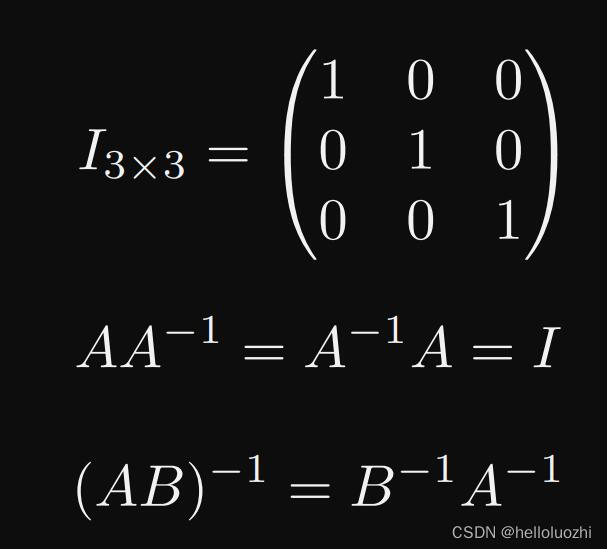
2.2.4 向量乘法的矩阵形式 Vector multiplication in Matrix form
向量a点乘b可以写为a的转置乘b
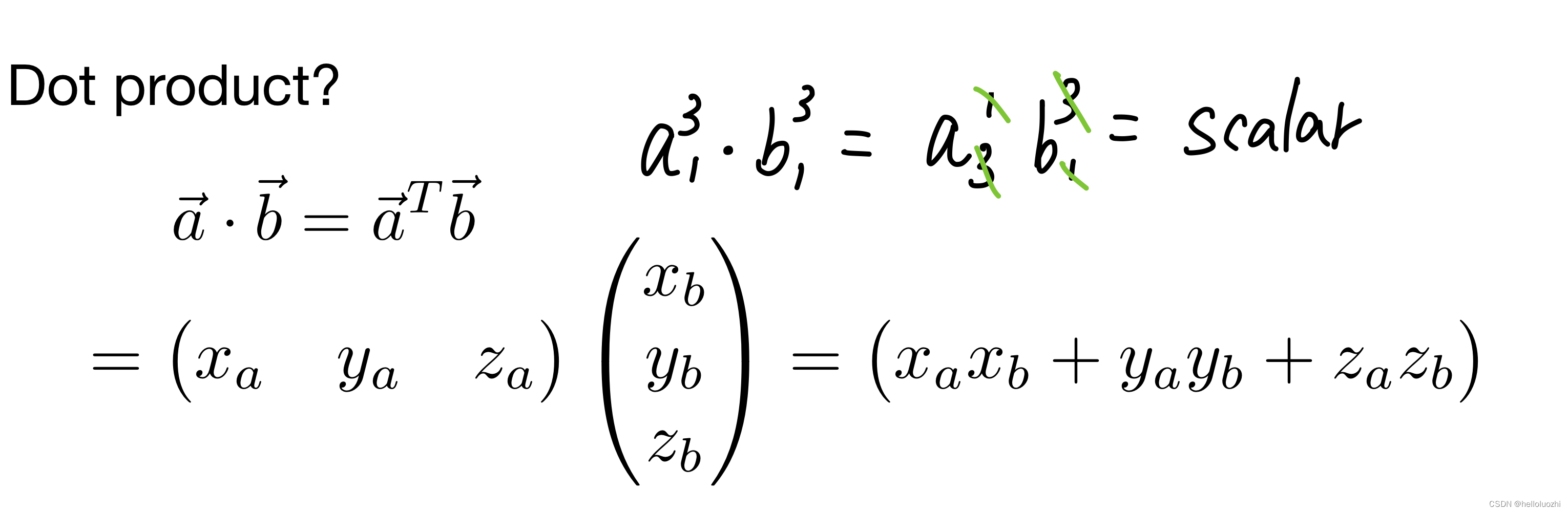
向量a叉乘b可以写为a的对偶矩阵乘b.(
怎么算A*呢?)
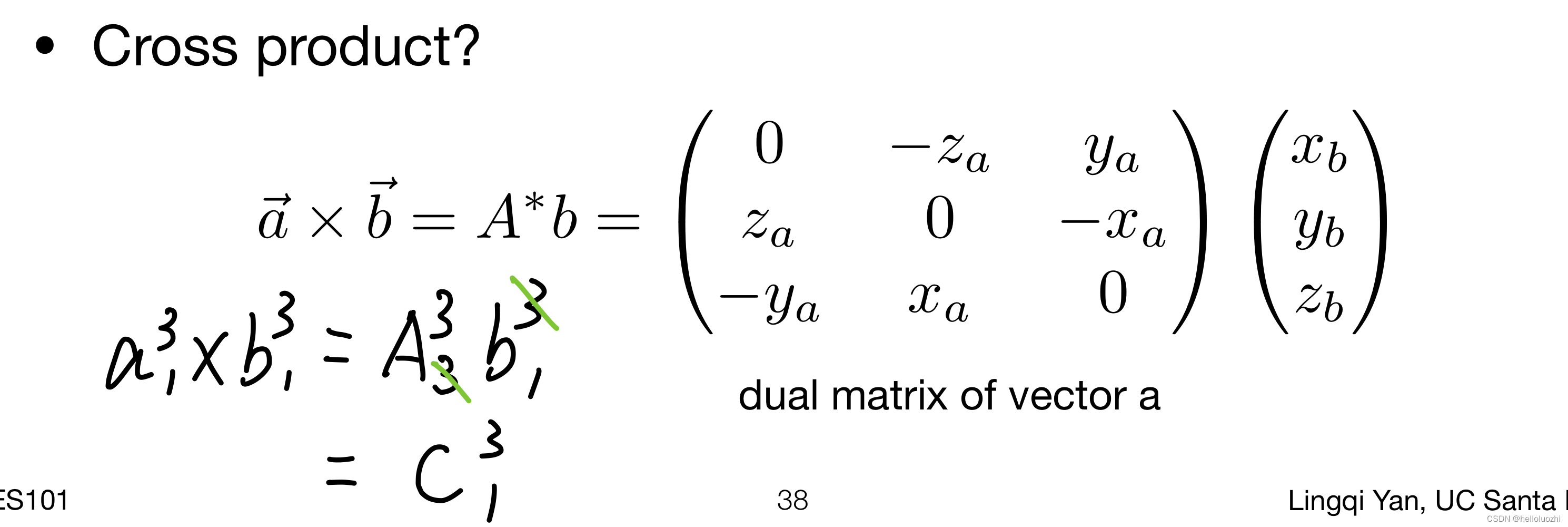
3 变换 transformation
学习目的:这是旋转 rotation,缩放 scaling,投影 projection的基础.
3.1 二维变换
缩放 Scale
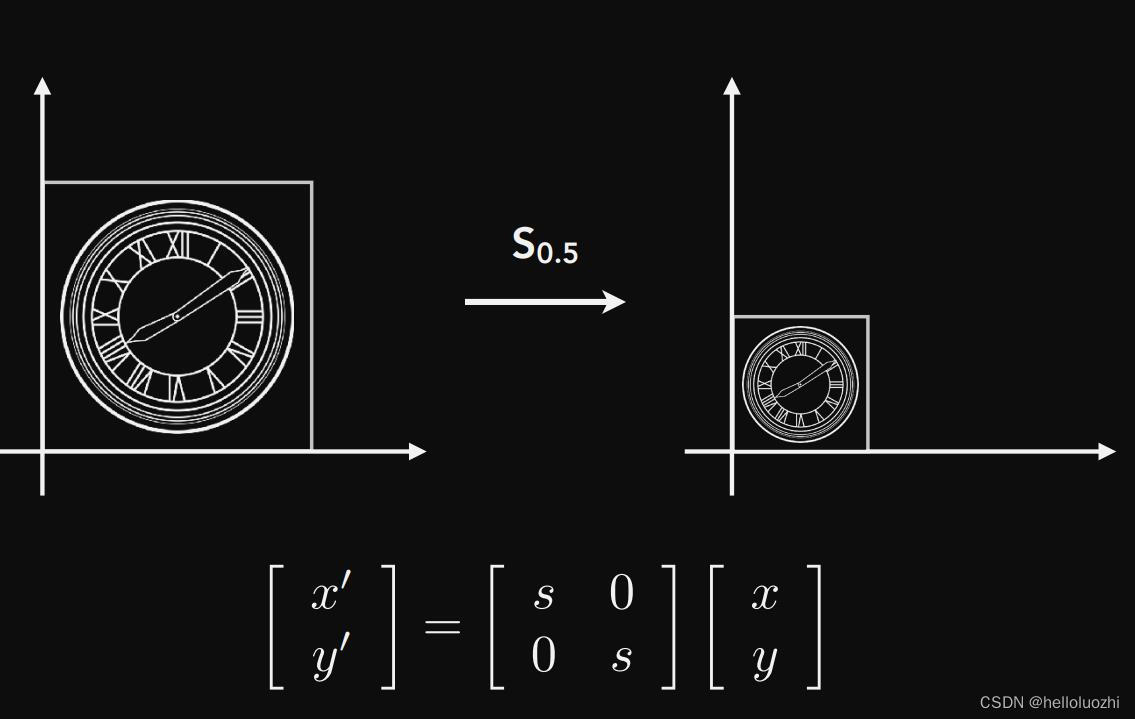
不完全缩放 Non-uniform scale

反射 reflection
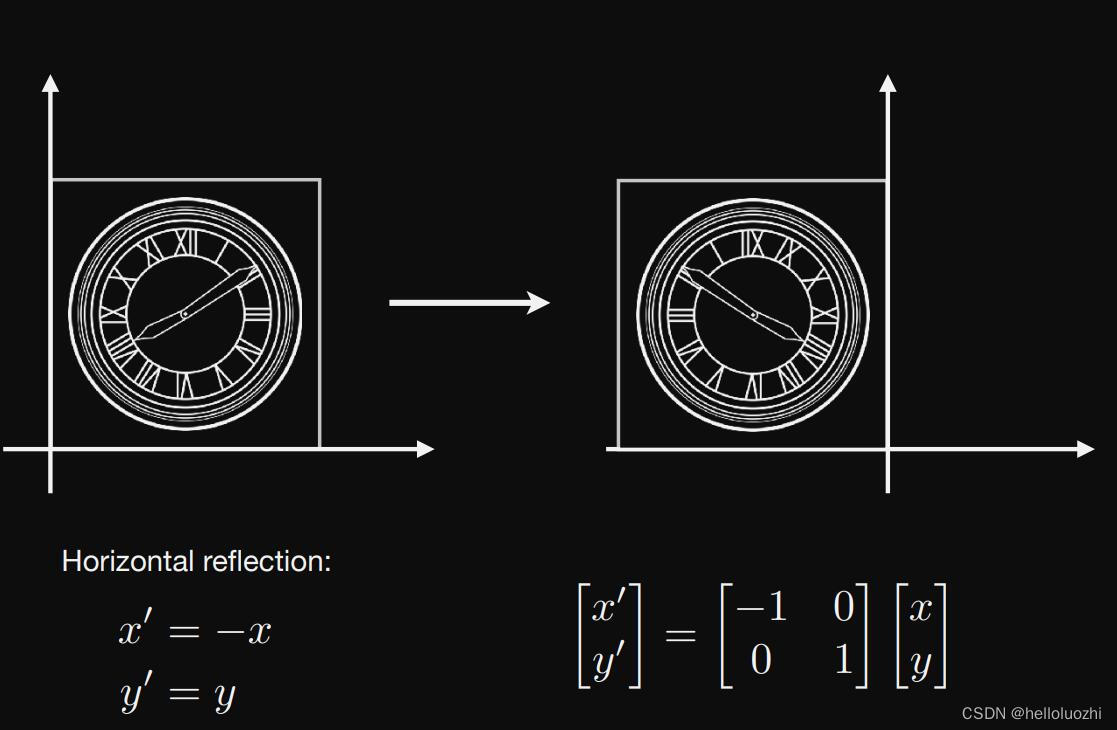
切变 shear(剪切)

y不变,x向右平移ay, x’ = x + ay. y’ = y.旋转 rotation
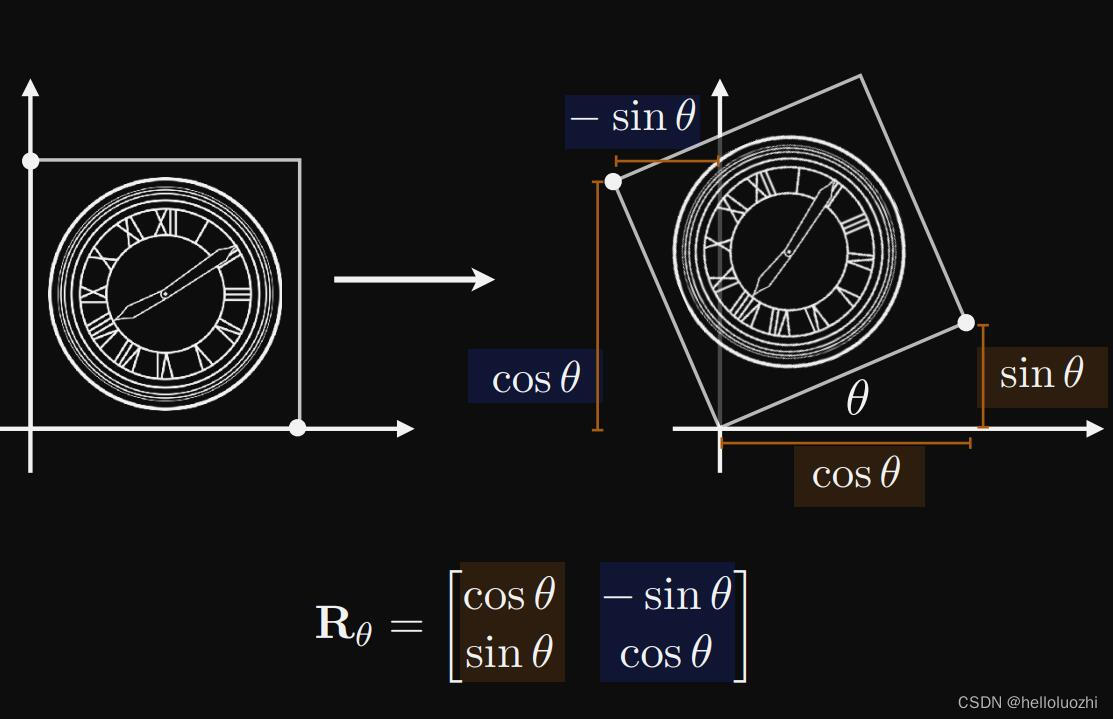
上面的旋转矩阵记忆:第一列就是(1,0)变换后坐标,第二列就是(0,1)变换后坐标.
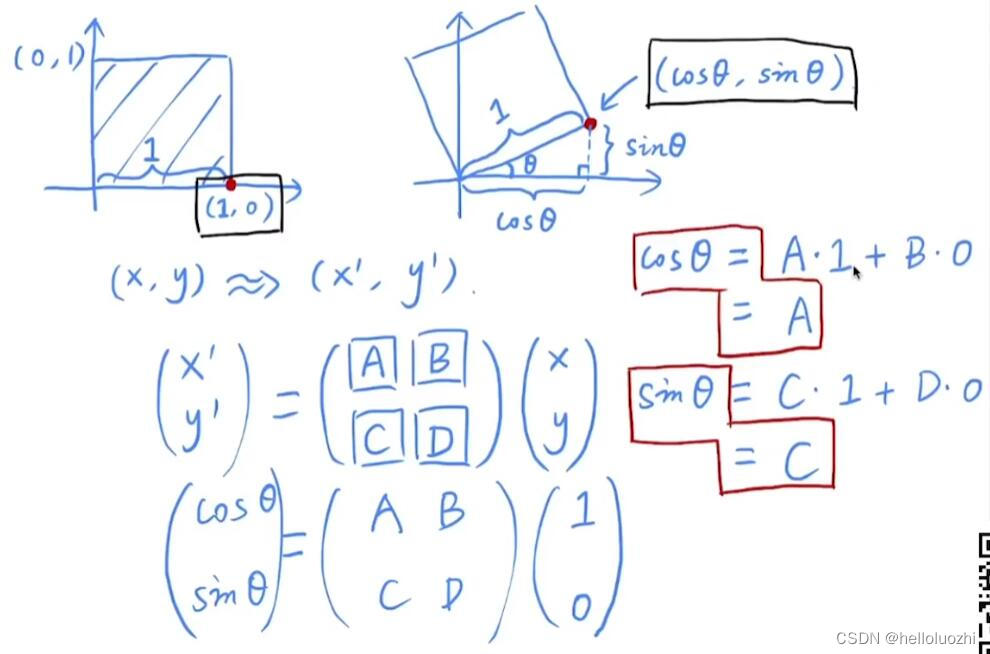
总结,以上的变换都写为
线性变换:
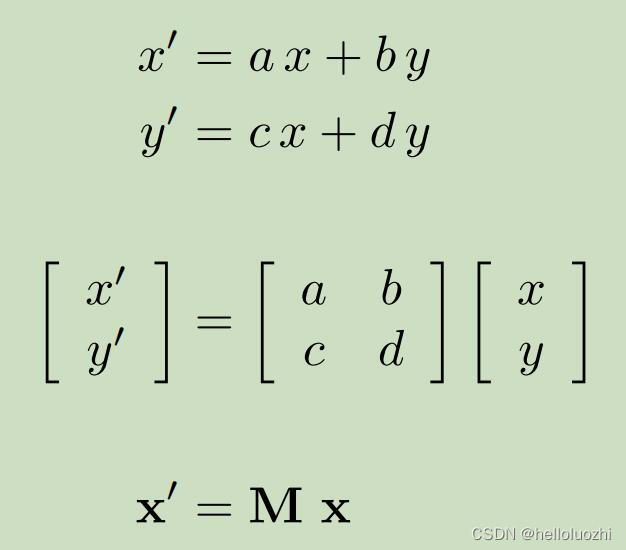
M是线性变换矩阵.
3.2 齐次坐标 Homogeneous coordianates
引入齐次坐标原因,
线性变换无法处理平移,如
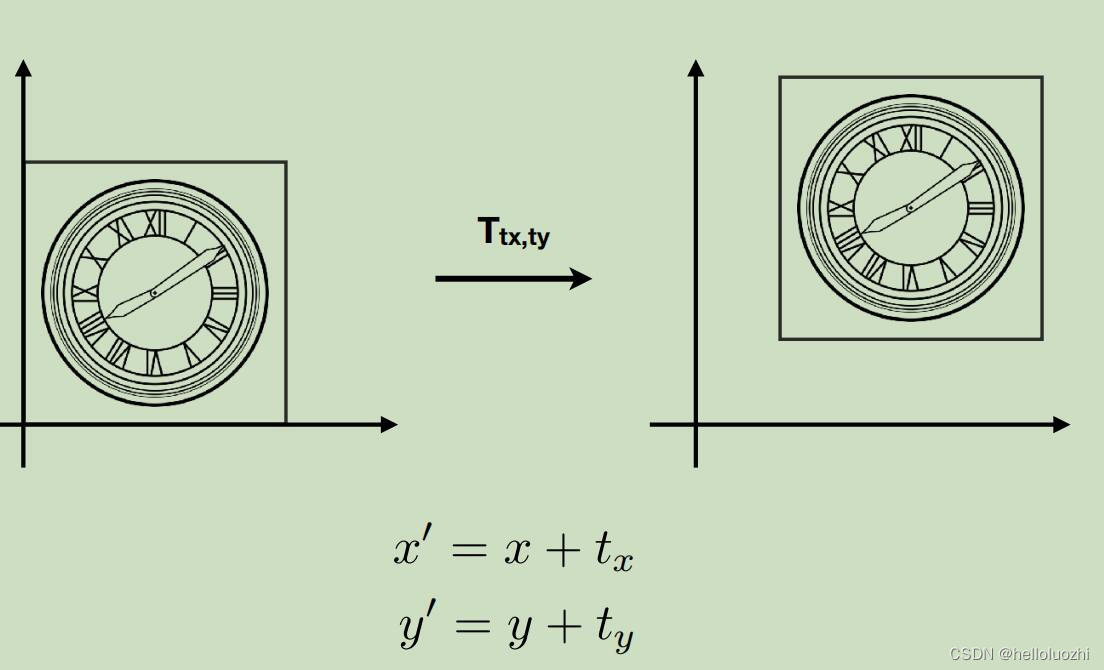
仿射affine变换
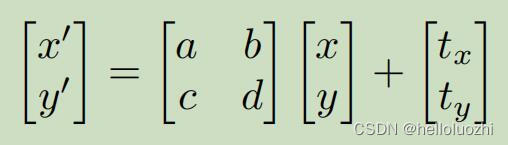
这里加了一项,不再是线性变换.怎么把上面的变换写为线性的呢? 现在引入齐次坐标

点加个1,向量加个0.(trade off),原因是考虑到点和向量的特性:
点加点还是点(1+1=2, 除以2等于1还是点),但点减点等于向量(1-1=0).

现在可以把缩放,旋转和平移重新写为

注意这里的变换矩阵(仿射affine变换)最后一行都是001,但其他情况时不一定是这样的.
3.3 逆变换 Inverse transform
逆变换的操作通过乘逆矩阵实现
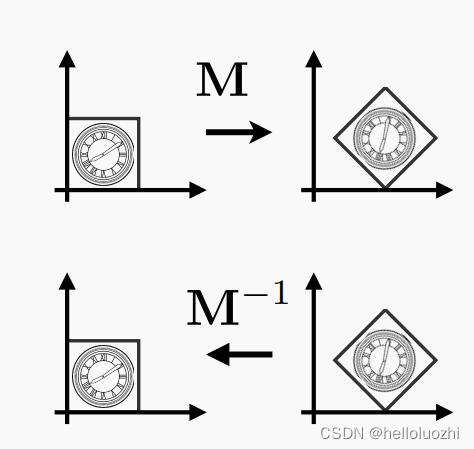
这也是逆矩阵的几何意义.所以也能理解为何矩阵乘逆矩阵等于单位矩阵,也就是对一个图像先操作然后逆操作等于没有操作.
3.4 组合变换 composing transforms
要做矩阵操作达到下面目的:
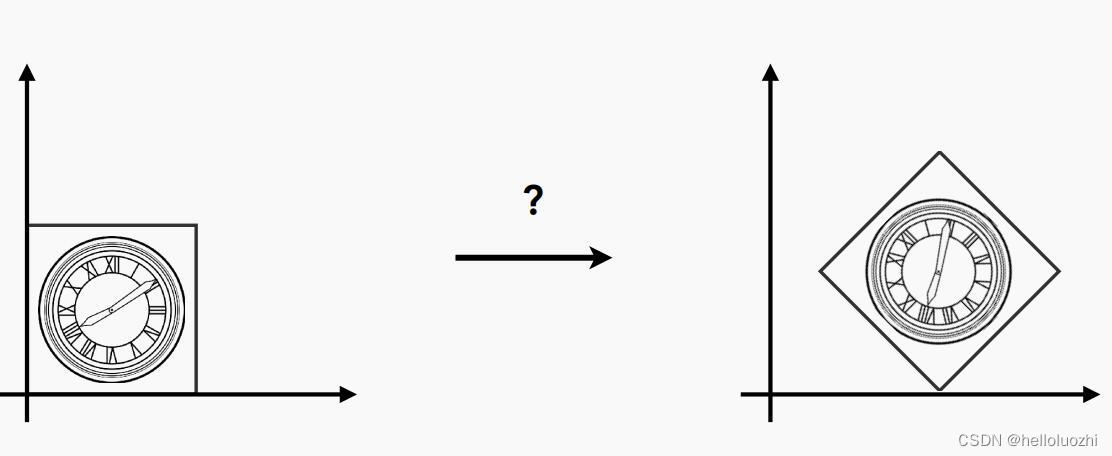
可以先旋转,再平移
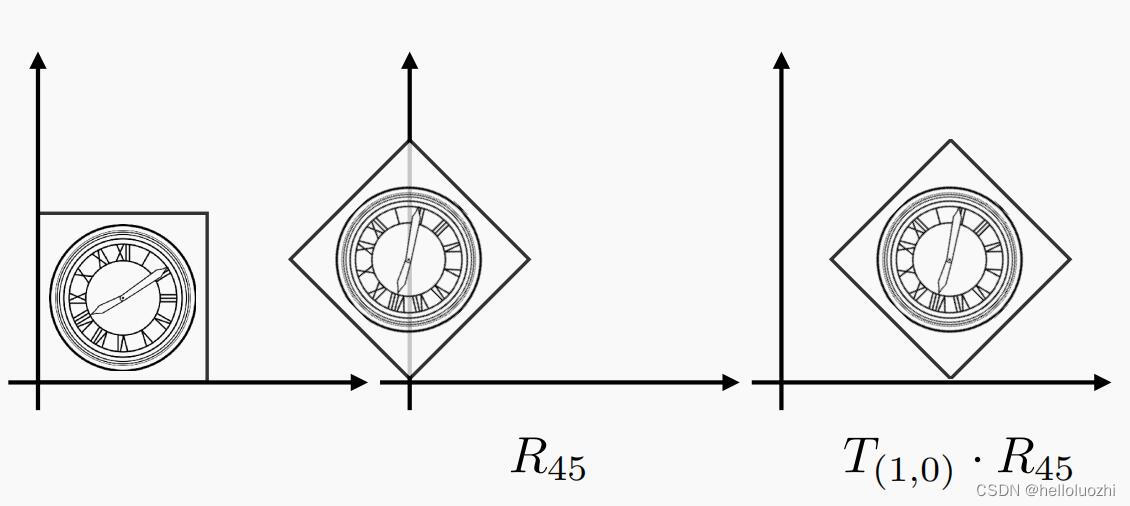
但不能交换矩阵的顺序,不然对应的几何操作变为
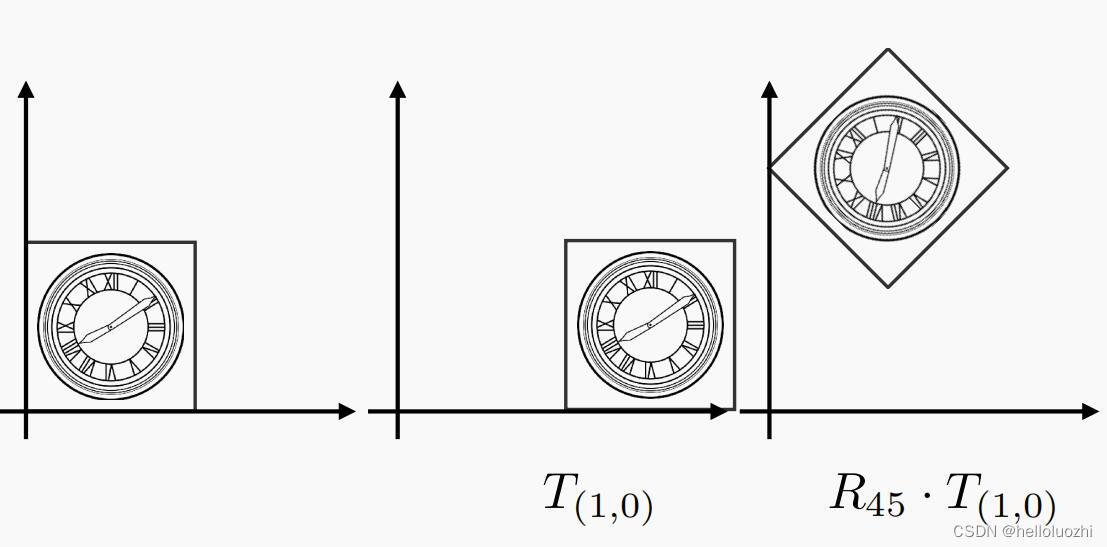
这也是矩阵不满足交换律的原因.所以正确的矩阵是:

注意矩阵的作用顺序是从右到左和向量结合.
- 虽然矩阵不满足交换律,但满足结合律.也就是
向量前的矩阵们可以写为一个大的矩阵,表示所有的变换:
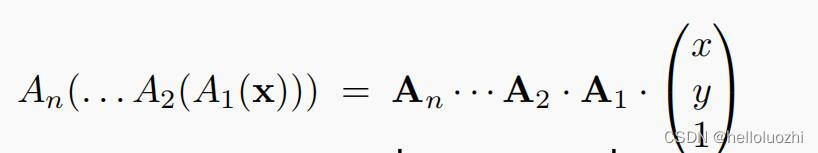
上面矩阵的组合可写为红色圈内

3.4.1 组合变换的分解应用—如何绕C点旋转?
Decomposng complex transforms
要绕C点旋转,先矩阵变换C点到原点,绕原点旋转,再矩阵变换回去.
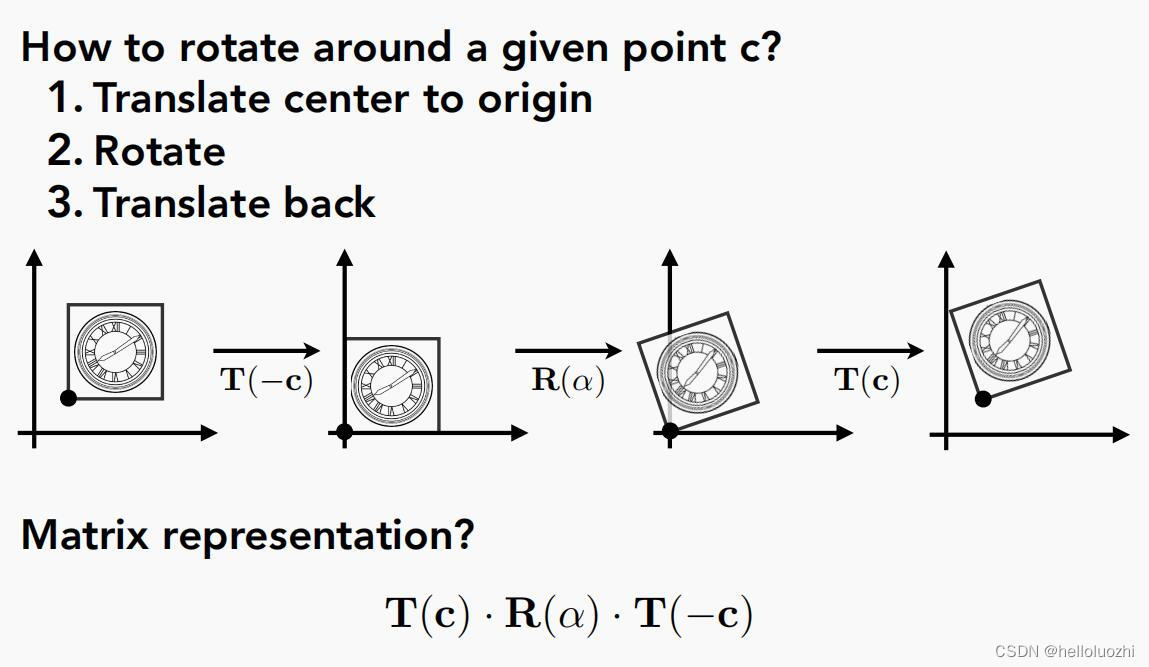
3.5 三维变换


注意上面矩阵对应的效果是先线性变换,再平移.