Motivation
3DGS 的 投影采用的是 CG系的投影矩阵 P P P, 默认相机的 principal point (相机光心) 位于图像的中点处。但是 实际应用的 绝大多数的 相机 并不满足这样一个设定, 因此我们 需要根据 f , c x , c y {f,c_x, c_y} f,cx,cy 这几个参数重新构建3D GS 的 投影矩阵。
3DGS 的相机模型的构建
原理:
目的: 将一个 相机View 坐标系的一个3D 点 变换到 NDC 坐标系
维基百科:https://www.songho.ca/opengl/gl_projectionmatrix.html
一共有如下3个坐标系
Eye 坐标系(View 坐标系) : ( x e , y e , z e ) (x_e,y_e,z_e) (xe,ye,ze)
View 坐标系 通过转化 矩阵 M p r o j M_{proj} Mproj 转化到Clip 坐标系。**先进行 缩放变换,**缩放之后的坐标是 ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp), 缩放之后继续做正交投影 【 就是把 (l,r)映射到 (-1,1)】,最后才可以变换到Clip坐标系下面的坐标 ( x c , y c , z c ) (x_c,y_c,z_c) (xc,yc,zc)。
Clip坐标系 : ( x c , y c , z c ) (x_c,y_c,z_c) (xc,yc,zc)
Clip 坐标系通过除以 齐次坐标系的 最后一个分量转换到 NDC 坐标系
NDC坐标系 : ( x n , y n , z n ) (x_n,y_n,z_n) (xn,yn,zn)
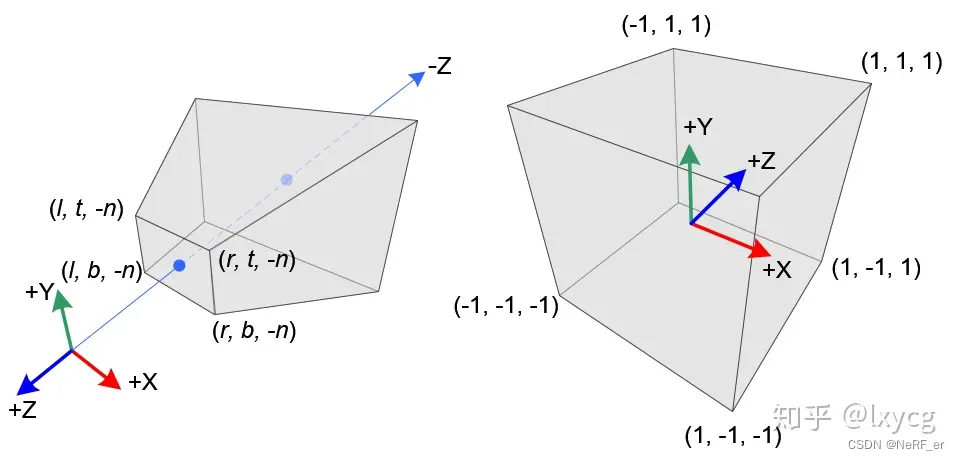
n为视锥体近面z坐标,f为远面z坐标,
t为视锥体top面z坐标,b为 bottom面y坐标,
r为视锥体right x坐标,left为左面x坐标,
1. 从 View 坐标系转化到 Clip 坐标系
主要是通过相似三角形的 原理去列方程:
x p = − n ⋅ x e z e = n ⋅ x e − z e x_p=\frac{-n \cdot x_e}{z_e}=\frac{n \cdot x_e}{-z_e} xp=ze−n⋅xe=−zen⋅xe
y p = − n ⋅ y e z e = n ⋅ y e − z e y_p=\frac{-n \cdot y_e}{z_e}=\frac{n \cdot y_e}{-z_e} yp=ze−n⋅ye=−zen⋅ye
z p z_p zp 坐标的求解,可以观看 闫令琪 的计算机图像学:有两个基本假设:
- Near 的平面的所有点 Z 缩放之后的 Z值不会发生变化;
- Far 平面的所有点 Z 缩放之后的 Z值不会发生变化;
得到了 缩放之后的 ( x p , y p , z p ) (x_p,y_p, z_p) (xp,yp,zp), 然后我们再通过线性变换做正交投影将Cuboid 的长和宽分别缩放到 一个 单位立方体, 即将 [l, r] ⇒ [-1, 1] and [b, t] ⇒ [-1, 1]。
Eq2:
x c = α x x p + β x x_c=\alpha_x x_p+\beta_x xc=αxxp+βx
y c = α y y p + β y y_c=\alpha_y y_p+\beta_y yc=αyyp+βy
将 x p x_p xp和 x e x_e xe 的关系带入上面Eq2式子当中。以 x 坐标为例,由于l对应-1,r对应1,求解出 α \alpha α 和 β \beta β我们有:
x c = 2 x p r − l − r + l r − l ( x p = n x e − z e ) = 2 ⋅ n ⋅ x e − z e r − l − r + l r − l = 2 n ⋅ x e ( r − l ) ( − z e ) − r + l r − l = 2 n r − l ⋅ x e − z e − r + l r − l = 2 n r − l ⋅ x e − z e + r + l r − l ⋅ z e − z e = ( 2 n r − l ⋅ x e + r + l r − l ⋅ z e ⏟ x c ) / − z e \begin{aligned} x_c& =\frac{2 x_p}{r-l}-\frac{r+l}{r-l} \quad\left(x_p=\frac{n x_e}{-z_e}\right) \\ & =\frac{2 \cdot \frac{n \cdot x_e}{-z_e}}{r-l}-\frac{r+l}{r-l} \\ & =\frac{2 n \cdot x_e}{(r-l)\left(-z_e\right)}-\frac{r+l}{r-l} \\ & =\frac{\frac{2 n}{r-l} \cdot x_e}{-z_e}-\frac{r+l}{r-l} \\ & =\frac{\frac{2 n}{r-l} \cdot x_e}{-z_e}+\frac{\frac{r+l}{r-l} \cdot z_e}{-z_e} \\ & =(\underbrace{\frac{2 n}{r-l} \cdot x_e+\frac{r+l}{r-l} \cdot z_e}_{x_c}) /-z_e\end{aligned} xc=r−l2xp−r−lr+l(xp=−zenxe)=r−l2⋅−zen⋅xe−r−lr+l=(r−l)(−ze)2n⋅xe−r−lr+l=−zer−l2n⋅xe−r−lr+l=−zer−l2n⋅xe+−zer−lr+l⋅ze=(xc r−l2n⋅xe+r−lr+l⋅ze)/−ze
y c = 2 y p t − b − t + b t − b ( y p = n y e − z e ) = 2 ⋅ n ⋅ y e − z e t − b − t + b t − b = 2 n ⋅ y e ( t − b ) ( − z e ) − t + b t − b = 2 n t − b ⋅ y e − z e − t + b t − b = 2 n t − b − z e ⋅ y e + t + b t − b − z e = ( 2 n t − b ⋅ y e + t + b t − b ⋅ z e ⏟ y c ) / − z e \begin{aligned} y_c & =\frac{2 y_p}{t-b}-\frac{t+b}{t-b} \quad\left(y_p=\frac{n y_e}{-z_e}\right) \\ & =\frac{2 \cdot \frac{n \cdot y_e}{-z_e}}{t-b}-\frac{t+b}{t-b} \\ & =\frac{2 n \cdot y_e}{(t-b)\left(-z_e\right)}-\frac{t+b}{t-b} \\ & =\frac{\frac{2 n}{t-b} \cdot y_e}{-z_e}-\frac{t+b}{t-b} \\ & =\frac{2 n}{\frac{t-b}{-z_e} \cdot y_e}+\frac{t+b}{\frac{t-b}{-z_e}} \\ & =(\underbrace{\frac{2 n}{t-b} \cdot y_e+\frac{t+b}{t-b} \cdot z_e}_{y_c}) /-z_e\end{aligned} yc=t−b2yp−t−bt+b(yp=−zenye)=t−b2⋅−zen⋅ye−t−bt+b=(t−b)(−ze)2n⋅ye−t−bt+b=−zet−b2n⋅ye−t−bt+b=−zet−b⋅ye2n+−zet−bt+b=(yc t−b2n⋅ye+t−bt+b⋅ze)/−ze
上面的恰好是 Clip 坐标系的 齐次坐标系。 发现 计算的 x c , y c x_c,y_c xc,yc 恰好是 除以了 − z e -z_e −ze, 因此 我们可以预先指定 齐次坐标的 第四项是: w c = − z e w_c = -z_e wc=−ze earlier。 下面是 Clip 坐标系的齐次坐标:
( x c y c z c w c ) = ( 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 ⋅ ⋅ ⋅ ⋅ 0 0 − 1 0 ) ( x e y e z e w e ) \left(\begin{array}{c}x_c \\ y_c \\ z_c \\ w_c\end{array}\right)=\left(\begin{array}{cccc}\frac{2 n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2 n}{t-b} & \frac{t+b}{t-b} & 0 \\ \cdot & \cdot & \cdot & \cdot \\ 0 & 0 & -1 & 0\end{array}\right)\left(\begin{array}{l}x_e \\ y_e \\ z_e \\ w_e\end{array}\right)
xcyczcwc
=
r−l2n0⋅00t−b2n⋅0r−lr+lt−bt+b⋅−100⋅0
xeyezewe
$Z的推导 和 x,y 没有关系。因此 上面的矩阵写成下面的形式:
( x c y c z c w c ) = ( 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 A B 0 0 − 1 0 ) ( x e y e z e w e ) \left(\begin{array}{c}x_c \\ y_c \\ z_c \\ w_c\end{array}\right)=\left(\begin{array}{cccc}\frac{2 n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2 n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & A & B \\ 0 & 0 & -1 & 0\end{array}\right)\left(\begin{array}{c}x_e \\ y_e \\ z_e \\ w_e\end{array}\right)
xcyczcwc
=
r−l2n0000t−b2n00r−lr+lt−bt+bA−100B0
xeyezewe
,
其中的 Z 项 单目提出来应该等于下面的式子:
z n = z c / w c = A z e + B w e − z c z_n=z_c / w_c=\frac{A z_e+B w_e}{-z_c} zn=zc/wc=−zcAze+Bwe
最后根据: Z_near 平面 和 Z_far 平面不会移动的原因,得到最后的 投影矩阵:
M p r o j = ( 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 − ( f + n ) f − n − 2 f n f − n 0 0 − 1 0 ) M_{proj}=\left(\begin{array}{cccc}\frac{2 n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2 n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2 f n}{f-n} \\ 0 & 0 & -1 & 0\end{array}\right) Mproj=
r−l2n0000t−b2n00r−lr+lt−bt+bf−n−(f+n)−100f−n−2fn0
Code:
3DGS 设定:
self.zfar = 100.0
self.znear = 0.01
下面这个 Projection_Matrix 的构建 和上面公式推导会有一点不一样的地方,尤其是对于 Z值的计算上,Github 上也有人提出过疑问。 矩阵的P[2,2] 有误, 但是作者又说 他在 Code 中没有 使用 Z的数值。
https://github.com/graphdeco-inria/gaussian-splatting/issues/388
https://github.com/graphdeco-inria/gaussian-splatting/issues/376
def getProjectionMatrix(znear, zfar, fovX, fovY):
tanHalfFovY = math.tan((fovY / 2)) ## 视场角一半的正切数值
tanHalfFovX = math.tan((fovX / 2))
## 得到 l,b,top,right
top = tanHalfFovY * znear
bottom = -top
right = tanHalfFovX * znear
left = -right
P = torch.zeros(4, 4)
z_sign = 1.0
P[0, 0] = 2.0 * znear / (right - left)
P[1, 1] = 2.0 * znear / (top - bottom)
P[0, 2] = (right + left) / (right - left)
P[1, 2] = (top + bottom) / (top - bottom)
P[3, 2] = z_sign
P[2, 2] = z_sign * zfar / (zfar - znear)
P[2, 3] = -(zfar * znear) / (zfar - znear)
return P
带有Cx, Cy的相机模型:
https://github.com/graphdeco-inria/gaussian-splatting/issues/144
def getProjectionMatrixShift(znear, zfar, focal_x, focal_y, cx, cy, width, height, fovX, fovY):
tanHalfFovY = math.tan((fovY / 2))
tanHalfFovX = math.tan((fovX / 2))
# the origin at center of image plane
top = tanHalfFovY * znear
bottom = -top
right = tanHalfFovX * znear
left = -right
# shift the frame window due to the non-zero principle point offsets
offset_x = cx - (width/2)
offset_x = (offset_x/focal_x)*znear
offset_y = cy - (height/2)
offset_y = (offset_y/focal_y)*znear
top = top + offset_y
left = left + offset_x
right = right + offset_x
bottom = bottom + offset_y
P = torch.zeros(4, 4)
z_sign = 1.0
P[0, 0] = 2.0 * znear / (right - left)
P[1, 1] = 2.0 * znear / (top - bottom)
P[0, 2] = (right + left) / (right - left)
P[1, 2] = (top + bottom) / (top - bottom)
P[3, 2] = z_sign
P[2, 2] = z_sign * zfar / (zfar - znear)
P[2, 3] = -(zfar * znear) / (zfar - znear)
return P
或者其他人 也给了 Projection 基于 相机内参的写法:
https://github.com/graphdeco-inria/gaussian-splatting/issues/399
P[0, 0] = 2 * fx / W
P[1, 1] = 2 * fy / H
P[0, 2] = 2 * (cx / W) - 0.5
P[1, 2] = 2 * (cy / H) - 0.5
P[2, 2] = -(zfar + znear) / (zfar - znear)
P[3, 2] = 1.0
P[2, 3] = -(2 * zfar * znear) / (zfar - znear)