一、概念
由顶点的非空有限集合 V(由 n>0 个顶点组成)与边的集合 EEE(顶点之间的关系)构成的结构。其形式化定义为 G=(V,E)。
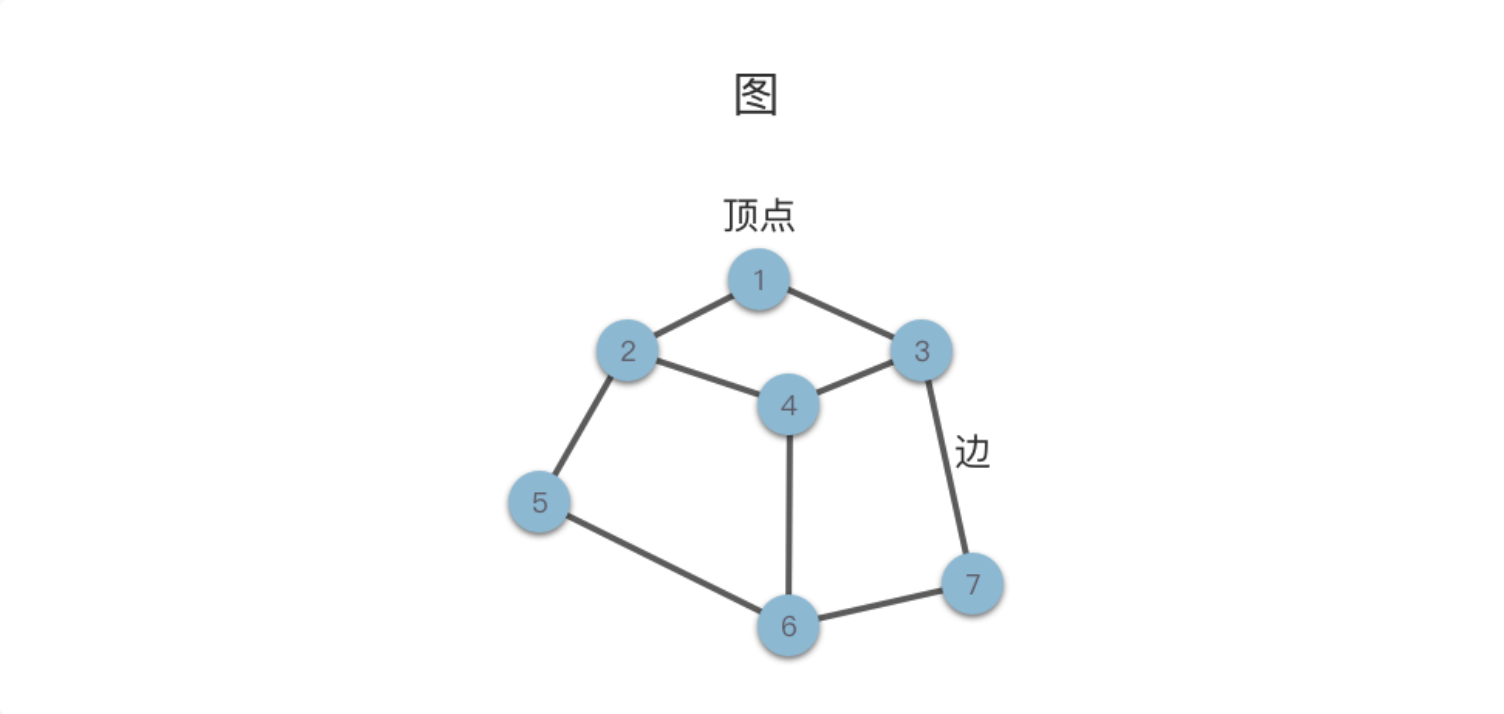
- 顶点(Vertex):图中的数据元素通常称为顶点,在下面的示意图中我们使用圆圈来表示顶点。
- 边(Edge):图中两个数据元素之间的关联关系通常称为边,在下面的示意图中我们使用连接两个顶点之间的线段来表示边。边的形式化定义为:e = <u,v>,表示从 u 到 v 的一条边,其中 u 称为起始点,v 称为终止点
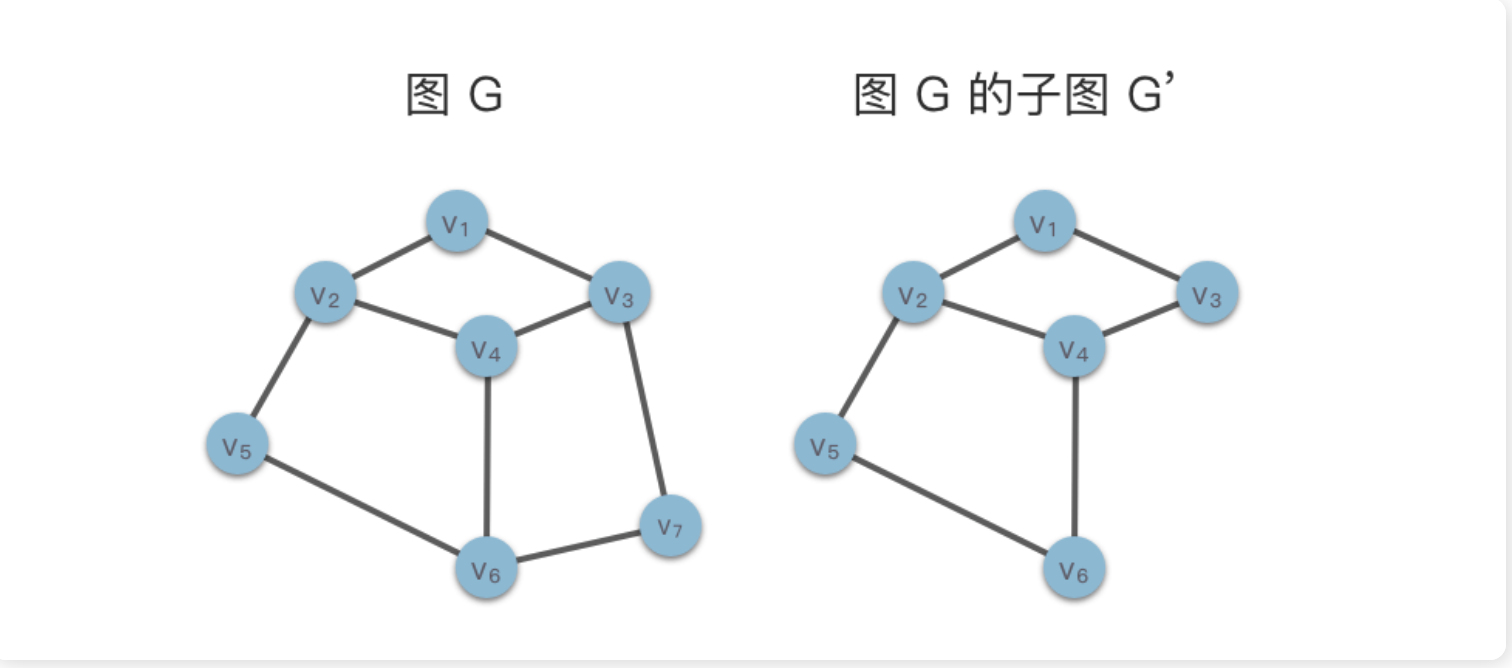
- 子图(Sub Graph):对于图 G=(V,E) 与 G′=(V′,E′ ),如果存在 V′⊆V ,E′⊆E,则称图 G′G^{'}G′ 是图 G`的一个子图。在下面的示意图中我们给出了一个图 G及其一个子图 G′。特别的,根据定义,G也是其自身的子图。
二、图的分类
1. 无向图和有向图
按照边是否有方向,我们可以将图分为两种类型:「无向图」和「有向图」。
- 无向图(Undirected Graph):如果图中的每条边都没有指向性,则称为无向图。例如朋友关系图、路线图都是无向图。
- 有向图(Directed Graph):如果图中的每条边都具有指向性,则称为有向图。例如流程图是有向图。
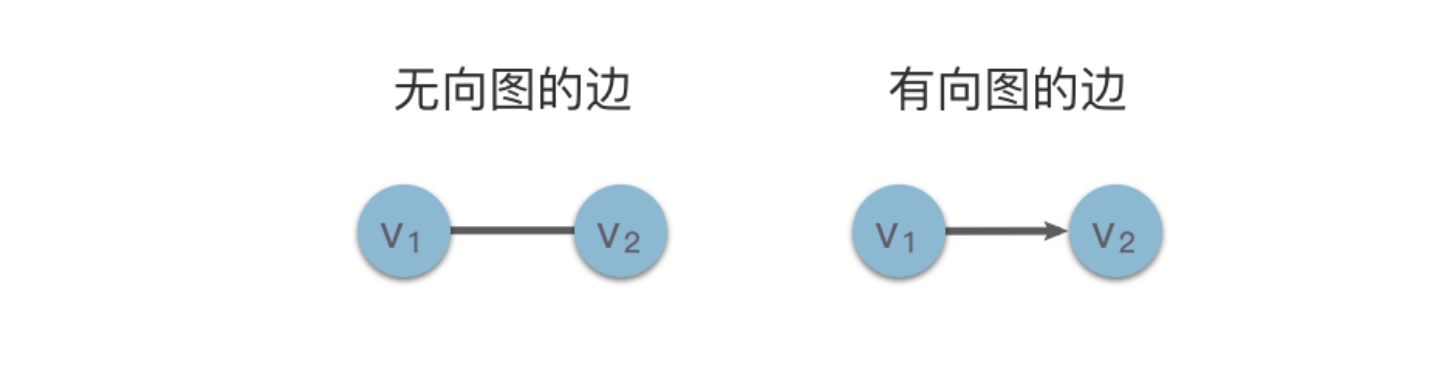
在无向图中,每条边都是由两个顶点组成的无序对。例如下图左侧中的顶点 v1 和顶点 v2之间的边记为 (v1,v2) 或 (v2,v1)。
在有向图中,有向边也被称为弧,每条弧是由两个顶点组成的有序对,例如下图右侧中从顶点 v1 到顶点 v2 的弧,记为 ⟨v1,v2⟩,v1被称为弧尾,v2被称为弧头,如下图所示
如果无向图中有 n 个顶点,则无向图中最多有 n×(n−1)/2n 条边。而具有 n×(n−1)/2n 条边的无向图称为 「完全无向图(Completed Undirected Graph)」。
如果有向图中有 n个顶点,则有向图中最多有 n×(n−1)n 条弧。而具有 n×(n−1)n 条弧的有向图称为 「完全有向图(Completed Directed Graph)」。
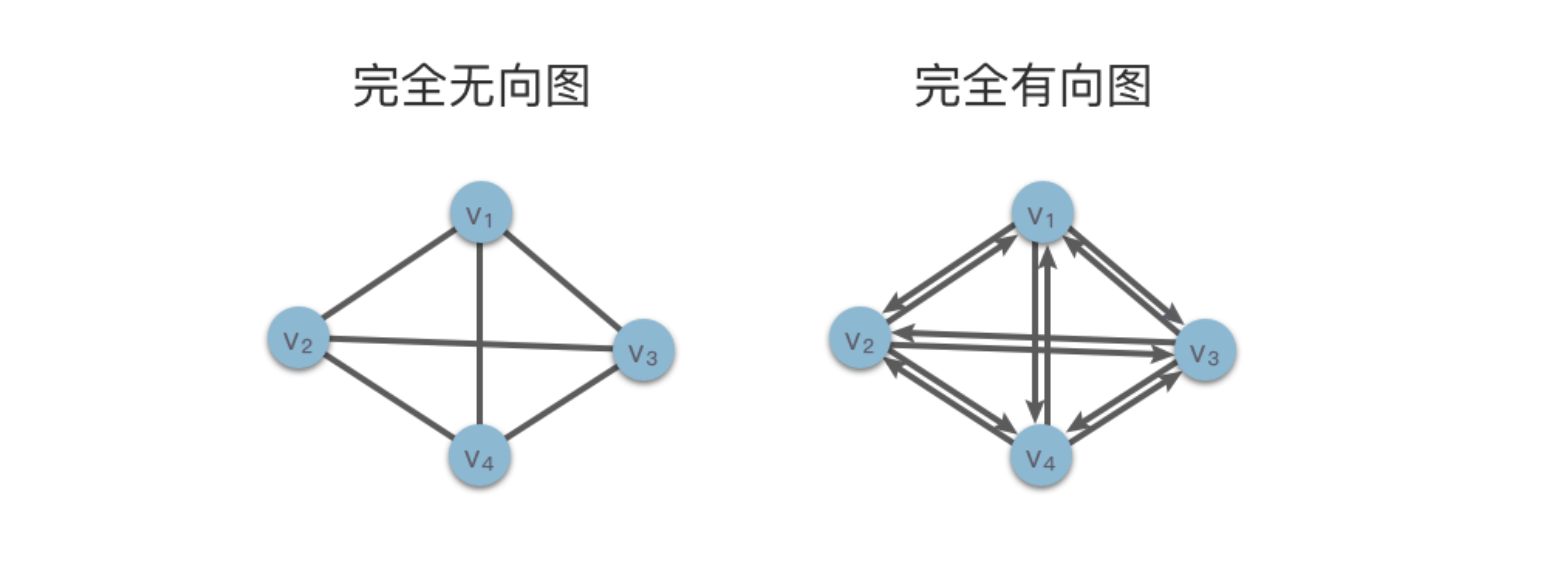
如下图所示,左侧为包含 444 个顶点的完全无向图,右侧为包含 444 个顶点的完全有向图
下面介绍一下无向图和有向图中一个重要概念 「顶点的度」。
- 顶点的度:与该顶点 vi相关联的边的条数,记为 TD(vi)。
例如上图左侧的完全无向图中,顶点 v3 的度为 3。
而对于有向图,我们可以将顶点的度分为 「顶点的出度」 和 「顶点的入度」。
- 顶点的出度:以该顶点 vi为出发点的边的条数,记为 OD(vi)。
- 顶点的入度:以该顶点 vi为终止点的边的条数,记为 ID(vi)。
- 有向图中某顶点的度 = 该顶点的出度 + 该顶点的入度,即 TD(vi)=OD(vi)+ID(vi)
例如上图右侧的完全有向图中,顶点 v3 的出度为 3,入度为 3,顶点 v3 的度为 3+3=6
2. 环形图和无环图

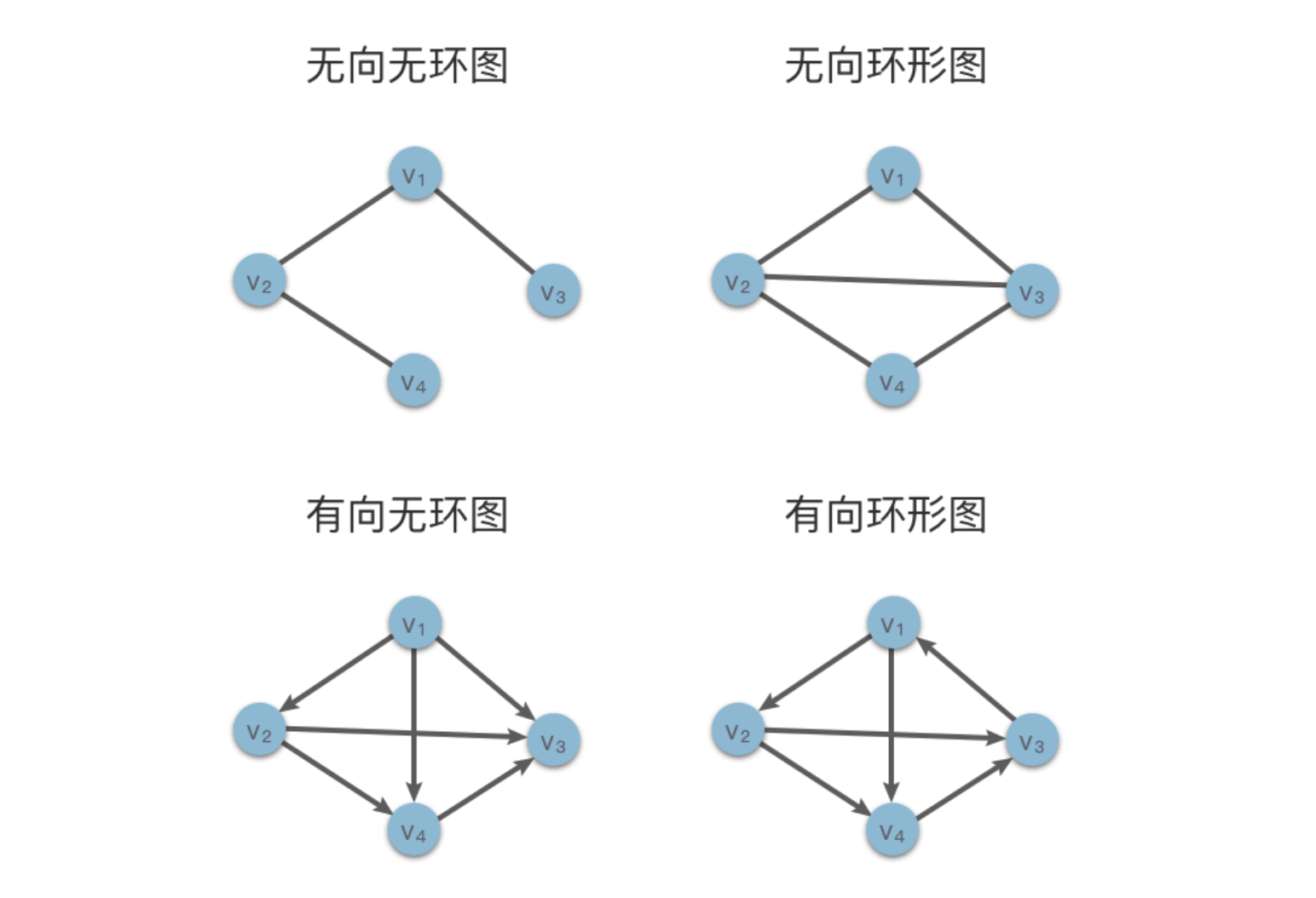
3. 带权图
时,图不仅需要表示顶点之间是否存在某种关系,还需要表示这一关系的具体细节。这时候我们需要在边上带一些数据信息,这些数据信息被称为 权。在具体应用中,权值可以具有某种具体意义,比如权值可以代表距离、时间以及价格等不同属性。
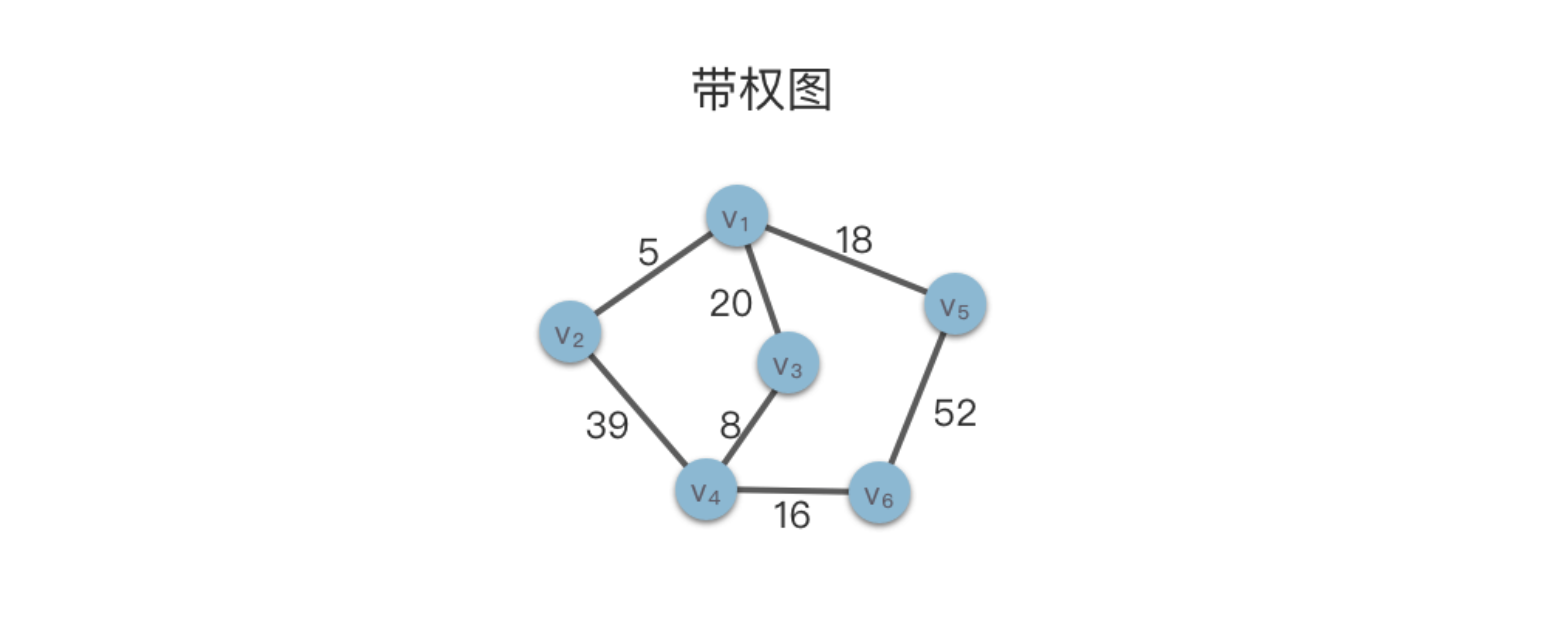
- 带权图:如果图的每条边都被赋以⼀个权值,这种图称为带权图。
- 网络:带权的连通⽆向图称为⽹络。
在下面的示意图中,我们给出了一个带权图的例子。
三、图的存储结构
图的结构比较复杂,我们需要表示顶点和边。一个图可能有任意多个(有限个)顶点,而且任何两个顶点之间都可能存在边。我们在实现图的存储时,重点需要关注边与顶点之间的关联关系,这是图的存储的关键。
图的存储可以通过「顺序存储结构」和「链式存储结构」来实现。其中顺序存储结构包括邻接矩阵和边集数组。链式存储结构包括邻接表、链式前向星、十字链表和邻接多重表。
1. 邻接矩阵
1.1. 概念
使用一个二维数组adjmatrix来存储顶点之间的邻接关系。
对于无权图来说,如果adjmatrix[i][j]为1,则说明顶点 vi到 vj存在边,如果adjmatrix[i][j]为0,则说明顶点 vi到 vj不存在边adjmatrix[i][j]为 w 并且 w≠∞则说明顶点 vi到 vj的权值为 w。如果adjmatrix[i][j] 为 ∞,则说明顶点 vi 到 vj不存在边。
对于带权图来说
- 优点:实现简单,并且可以直接查询顶点 vi 与 vj之间是否有边存在,还可以直接查询边的权值。
- 缺点:初始化效率和遍历效率较低,空间开销大,空间利用率低,并且不能存储重复边,也不便于增删节点。如果当顶点数目过大(比如当 n>10^5)时,使用邻接矩阵建立一个 n*n的二维数组不太现实
1.2. 代码实现
class Graph {
// 构造函数,初始化图的顶点个数
constructor(verCount) {
this.verCount = verCount;
// 使用二维数组表示邻接矩阵
this.adjMatrix = new Array(verCount).fill(null).map(() => new Array(verCount).fill(null));
}
// 添加边
addEdge(vi, vj, val) {
if (!this.isValid(vi) || !this.isValid(vj)) {
// 抛出错误,指示顶点无效
throw new Error(`${vi} 或 ${vj} 不是有效的顶点。`);
}
// 在邻接矩阵中设置边的权值
this.adjMatrix[vi][vj] = val;
}
// 获取边的权值
getEdge(vi, vj) {
if (!this.isValid(vi) || !this.isValid(vj)) {
// 抛出错误,指示顶点无效
throw new Error(`${vi} 或 ${vj} 不是有效的顶点。`);
}
// 返回邻接矩阵中的边权值
return this.adjMatrix[vi][vj];
}
// 打印图的边
printGraph() {
for (let vi = 0; vi < this.verCount; vi++) {
for (let vj = 0; vj < this.verCount; vj++) {
const val = this.getEdge(vi, vj);
if (val !== null && val !== undefined) {
// 打印边的信息
console.log(`${vi} - ${vj} : ${val}`);
}
}
}
}
// 判断顶点是否有效
isValid(v) {
// 判断顶点是否在有效范围内
return 0 <= v && v < this.verCount;
}
}
// 示例用法
const graph = new Graph(5);
const edges = [[1, 2, 5], [2, 1, 5], [1, 3, 30], [3, 1, 30], [2, 3, 14], [3, 2, 14], [2, 4, 26], [4, 2, 26]];
// 添加边到图中
edges.forEach(([vi, vj, val]) => {
graph.addEdge(vi, vj, val);
});
try {
// 尝试获取边的权值和打印图的边
console.log(graph.getEdge(3, 4));
graph.printGraph();
} catch (error) {
// 捕获并打印错误信息
console.error(error.message);
}
2. 边集数组
2.1. 概念
使用一个数组来存储存储顶点之间的邻接关系。数组中每个元素都包含一条边的起点 vi、终点 vj和边的权值 val(如果是带权图)
2.2. 代码实现
class EdgeNode {
// 边信息类
constructor(vi, vj, val) {
this.vi = vi; // 边的起点
this.vj = vj; // 边的终点
this.val = val; // 边的权值
}
}
class Graph {
// 基本图类,采用边集数组表示
constructor() {
this.edges = []; // 边数组
}
// 图的创建操作,edges 为边信息
createGraph(edges = []) {
edges.forEach(([vi, vj, val]) => {
this.add_edge(vi, vj, val);
});
}
// 向图的边数组中添加边:vi - vj,权值为 val
add_edge(vi, vj, val) {
const edge = new EdgeNode(vi, vj, val); // 创建边节点
this.edges.push(edge); // 将边节点添加到边数组中
}
// 获取 vi - vj 边的权值
get_edge(vi, vj) {
for (const edge of this.edges) {
if (vi === edge.vi && vj === edge.vj) {
return edge.val;
}
}
return null;
}
// 根据边数组打印图
printGraph() {
this.edges.forEach(edge => {
console.log(`${edge.vi} - ${edge.vj} : ${edge.val}`);
});
}
}
// 示例用法
const graph = new Graph();
const edges = [[1, 2, 5], [1, 5, 6], [2, 4, 7], [4, 3, 9], [3, 1, 2], [5, 6, 8], [6, 4, 3]];
// 添加边到图中
graph.createGraph(edges);
// 获取边的权值和打印图的边
console.log(graph.get_edge(3, 4));
graph.printGraph();
3. 邻接表
3.1. 概念
使用顺序存储和链式存储相结合的存储结构来存储图的顶点和边。其数据结构包括两个部分,其中一个部分是数组,主要用来存放顶点的数据信息,另一个部分是链表,用来存放边信息。
在邻接表的存储方法中,对于对图中每个顶点 viv_ivi 建立一个线性链表,把所有邻接于 viv_ivi 的顶点链接到单链表上。这样对于具有 n 个顶点的图而言,其邻接表结构由 n 个线性链表组成。
然后我们在每个顶点前边设置一个表头节点,称之为「顶点节点」。每个顶点节点由「顶点域」和「指针域」组成。其中顶点域用于存放某个顶点的数据信息,指针域用于指出该顶点第 1 条边所对应的链节点。
为了方便随机访问任意顶点的链表,通常我们会使用一组顺序存储结构(数组)存储所有「顶点节点」部分,顺序存储结构(数组)的下标表示该顶点在图中的位置。
3.2. 代码实现
// 边信息类
class EdgeNode {
// 构造函数,初始化边的终点、权值和下一条边
constructor(vj, val) {
this.vj = vj; // 边的终点
this.val = val; // 边的权值
this.next = null; // 下一条边
}
}
// 顶点信息类
class VertexNode {
// 构造函数,初始化边的起点和下一个邻接点
constructor(vi) {
this.vi = vi; // 边的起点
this.head = null; // 下一个邻接点
}
}
// 图类,采用邻接表表示
class Graph {
// 构造函数,初始化图的顶点个数和顶点数组
constructor(verCount) {
this.verCount = verCount;
this.vertices = [];
for (let vi = 0; vi < verCount; vi++) {
const vertex = new VertexNode(vi);
this.vertices.push(vertex);
}
}
// 判断顶点 v 是否有效
isValid(v) {
return 0 <= v && v < this.verCount;
}
// 图的创建操作,edges 为边信息
createGraph(edges = []) {
edges.forEach(([vi, vj, val]) => {
this.addEdge(vi, vj, val);
});
}
// 向图的邻接表中添加边:vi - vj,权值为 val
addEdge(vi, vj, val) {
if (!this.isValid(vi) || !this.isValid(vj)) {
throw new Error(`${vi} 或 ${vj} 不是有效的顶点。`);
}
const vertex = this.vertices[vi];
const edge = new EdgeNode(vj, val);
edge.next = vertex.head;
vertex.head = edge;
}
// 获取 vi - vj 边的权值
getEdge(vi, vj) {
if (!this.isValid(vi) || !this.isValid(vj)) {
throw new Error(`${vi} 或 ${vj} 不是有效的顶点。`);
}
const vertex = this.vertices[vi];
let curEdge = vertex.head;
while (curEdge) {
if (curEdge.vj === vj) {
return curEdge.val;
}
curEdge = curEdge.next;
}
return null;
}
// 根据邻接表打印图的边
printGraph() {
for (const vertex of this.vertices) {
let curEdge = vertex.head;
while (curEdge) {
console.log(`${vertex.vi} - ${curEdge.vj} : ${curEdge.val}`);
curEdge = curEdge.next;
}
}
}
}
// 示例用法
const graph = new Graph(7);
const edges = [[1, 2, 5], [1, 5, 6], [2, 4, 7], [4, 3, 9], [3, 1, 2], [5, 6, 8], [6, 4, 3]];
// 添加边到图中
graph.createGraph(edges);
// 获取边的权值和打印图的边
console.log(graph.getEdge(3, 4));
graph.printGraph();
四、图论问题应用
图论和图论算法在计算机科学中扮演这很重要的角色,它提供了对很多问题都有效的一种简单而系统的建模方式。很多实际问题都可以转化为图论问题,然后使用图论的景点算法加以解决。例如:
- 集成电路的设计和布线。
- 互联网和路由移动电话网的路由设计。
- 工程项目的计划安排问题。
常见的图论问题应用大概可以分为以下几类:图的遍历问题、图的连通性问题、图的生成树问题、图的最短路径问题、图的网络流问题、二分图问题 等等