目录
1.二叉树的概念
二叉树是一种特殊的树型结构,是非线性的,树是递归定义的。
二叉树是每个节点最多有两个子节点(左子节点和右子节点)的树结构。
可以为空(无节点),或由根节点(也叫父节点)和左右子树(左右子树也要满足二叉树)组成。
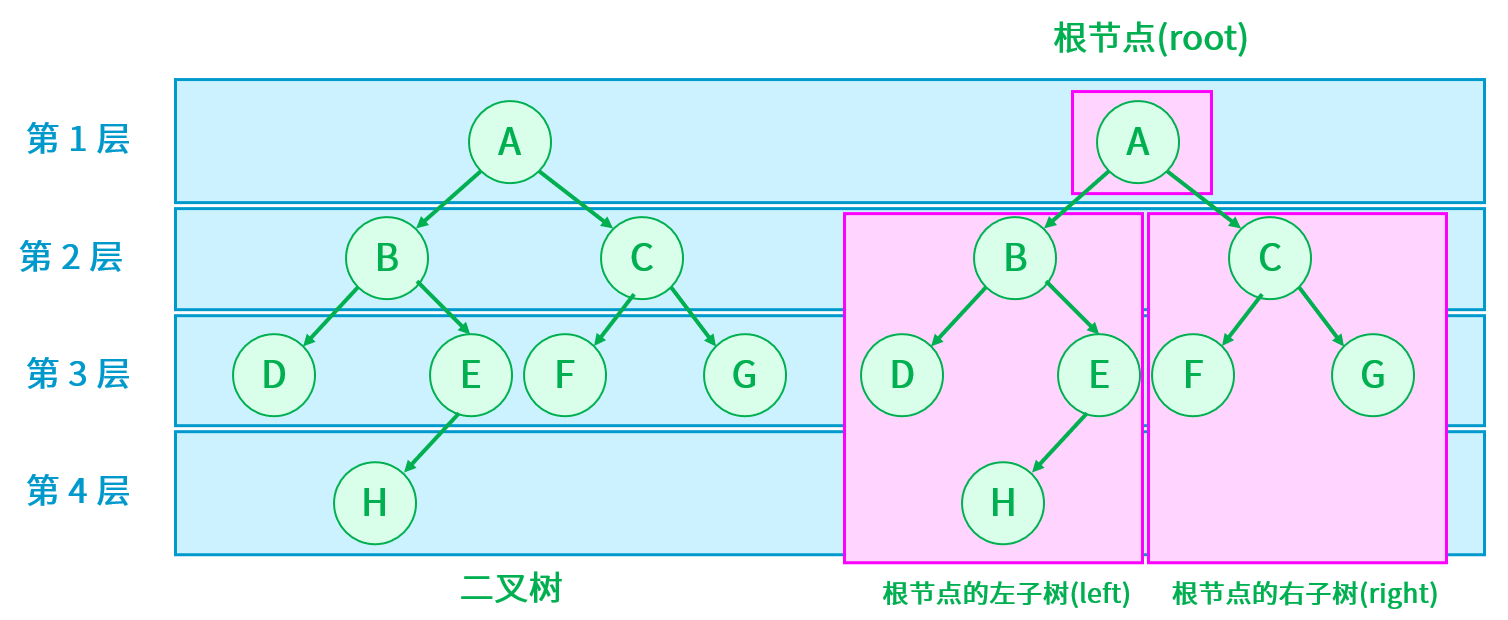
- 二叉树的每个节点最多有两个子节点,即二叉树不存在度大于 2 的节点。
- 二叉树的左右左右节点一般称为左子树和右子树,普通二叉树可以存在左子树为空或者右子树为空或者左右子树都为空。
2. 特殊的二叉树
满二叉树:一棵二叉树,如果每一层的节点数都达到最大值,那么这棵树就是一个满二叉树。也就是说,如果一个层数为 K 的二叉树,根节点定义为第 1 层,那么每一层的节点数都满足 2^(K - 1),那么它就是一棵满二叉树。
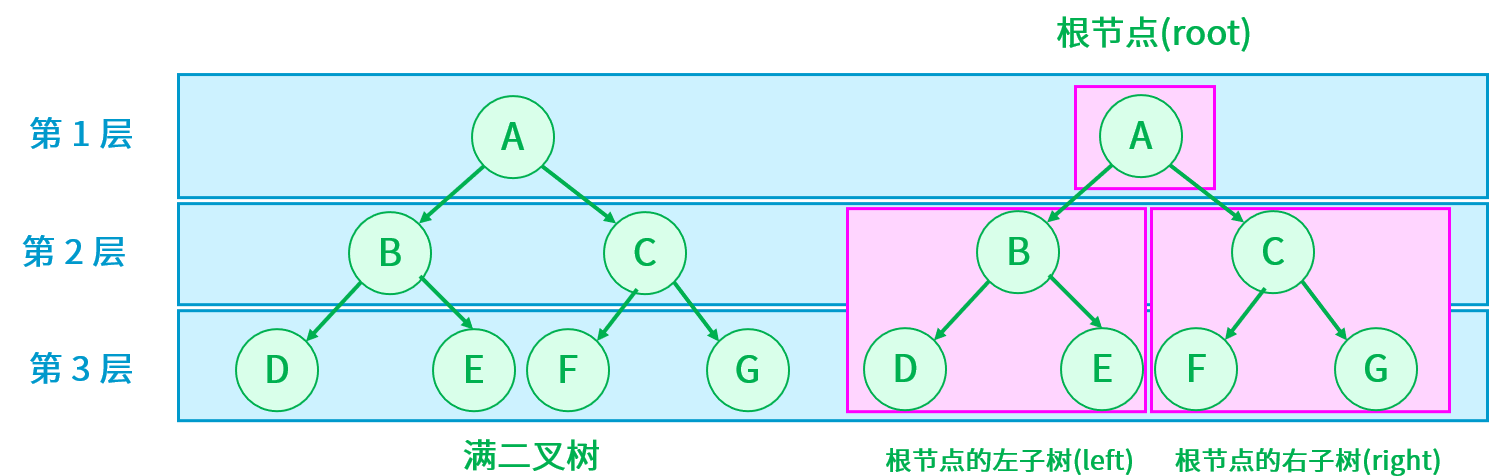
完全二叉树:对于完全二叉树的概念,书面表达为对于层数为 K,有 n 个节点的二叉树,当且仅当每一个节点都与层数为 K 的满二叉树编号从 0 至 n - 1 的节点一 一对应,称为完全二叉树。读完概念可能比较晦涩难懂,但其实很好理解,一棵二叉树,每一层都从左至右依次编号,此时二叉树就满足完全二叉树。
比如在二叉树的概念里的图,就不是一棵完全二叉树,但是如果改变节点 H 的位置,就可以使其变成一棵完全二叉树。
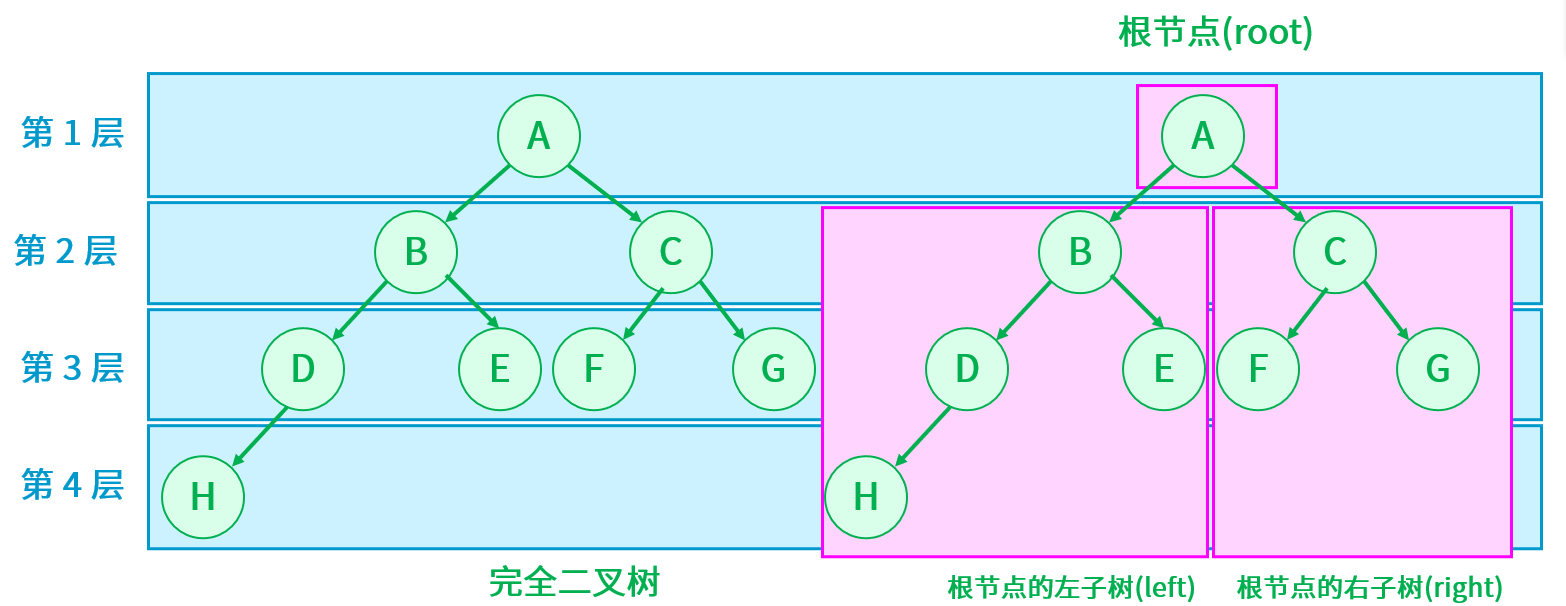
所以,满二叉树是一种特殊的完全二叉树。
3.二叉树的性质
- 若规定根节点的层数为 1 ,则一棵非空二叉树的第 K 层上至多有 2^(K - 1) 个节点
- 若规定根节点的深度为 1,则一棵深度为 K 的二叉树至多有 2^K - 1 个节点
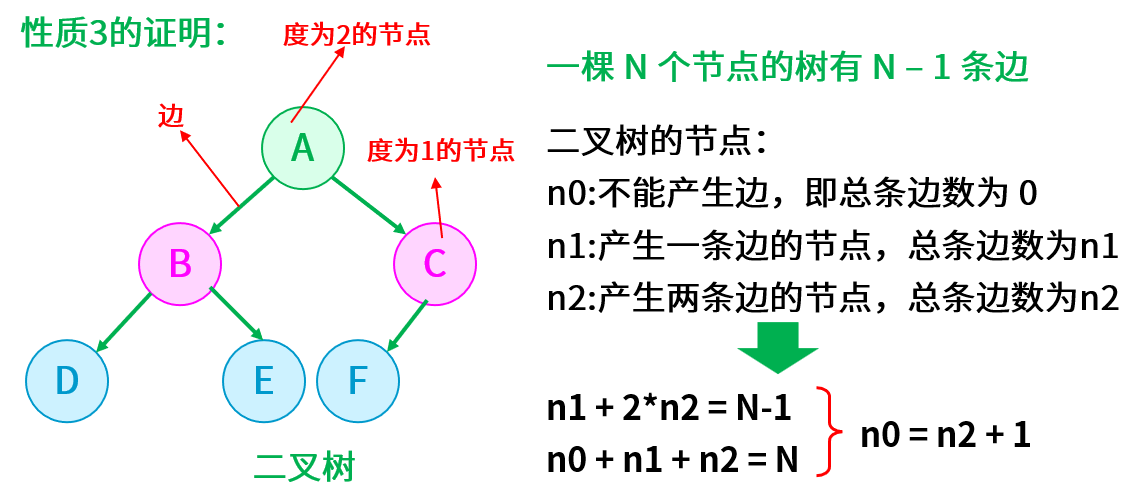
- 对任意一棵二叉树,如果叶子节点个数为 n0,度为 2 的节点为 n2,那么有 n0 = n2 + 1
- 具有 n 个节点的完全二叉树的深度 K = log2(n + 1)(以 2 为底)向上取整
- 对于具有 n 个节点的完全二叉树,如果按照从上到下从左到右依次从0开始编号,那么对于第 i 个节点有:若 i > 0,则根节点为 ( i - 1 ) / 2;若 2i + 1 < n ,则左子树节点为 2i + 1;若 2i + 2 < n 右子树节点为 2i + 2
4.二叉树的存储
二叉树的存储结构分为 顺序存储结构(数组表示) 和 链式存储结构(指针/引用表示)
顺序存储结构通常用在完全二叉树或满二叉树,而链式存储结构适用于任意的二叉树。本文主要介绍链式存储。
5. 二叉树的创建
二叉树的创建有多种形式,比如手动创建,递归前序创建(手动写空节点),层序遍历创建,中序 + 前序(后序)遍历创建等,但是方法虽然很多,在现有基础上是不能完全创建的,因此想要了解后面的创建的方法,需要借助手动创建来理解二叉树的遍历、二叉树的高度、节点个数等。
以这张图为例,手动创建一棵二叉树:
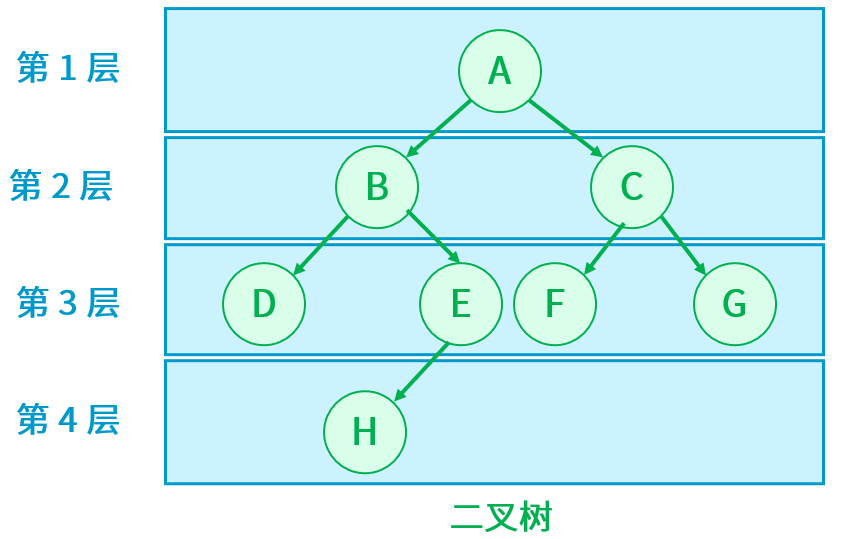
public class BinaryTree {
public static class TreeNode {
public char val;//节点元素
public TreeNode left;//左子树
public TreeNode right;//右子树
public TreeNode(char val) {
this.val = val;
}
}
//手动创建一棵二叉树,并返回根节点A
public TreeNode createTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.left = H;
return A;
}
}
6.二叉树的遍历
学习二叉树结构,最简单的方式就是对二叉树进行遍历。遍历,指的是沿着某一条线进行搜索,依次对树中的每个节点仅做一次的访问。当访问全部节点后,就完成一次遍历。
二叉树虽然每个节点只有两个子树,但是在每个节点往不同方向遍历时,每次得到的遍历结果都会不一样。因此,在数据结构中,约定了四种遍历方式,分别是前序遍历、中序遍历、后序遍历和层数遍历。
- 前序遍历:先访问根节点——>再访问根的左子树——>最后访问根的右子树。学习时可以记为根左右
- 中序遍历:先访问根的左子树——>再访问根节点——>最后访问根的右子树。学习时可以记为左根右
- 后续遍历:先访问根的左子树——>再访问根的右子树——>最后访问根节点。学习时可以记为左右根
- 层序遍历:对二叉树的每一层依次访问,第一层访问结束再进行第二层的访问,以此类推,直至访问全部节点为止。
以下遍历图都以前面手动创建的二叉树为例。
6.1 前序遍历
前序遍历:先访问根节点——>再访问根的左子树——>最后访问根的右子树。
(静态流程图比较乱,建议学习的读者可以用笔手动跟着画一个方便理解哦~)
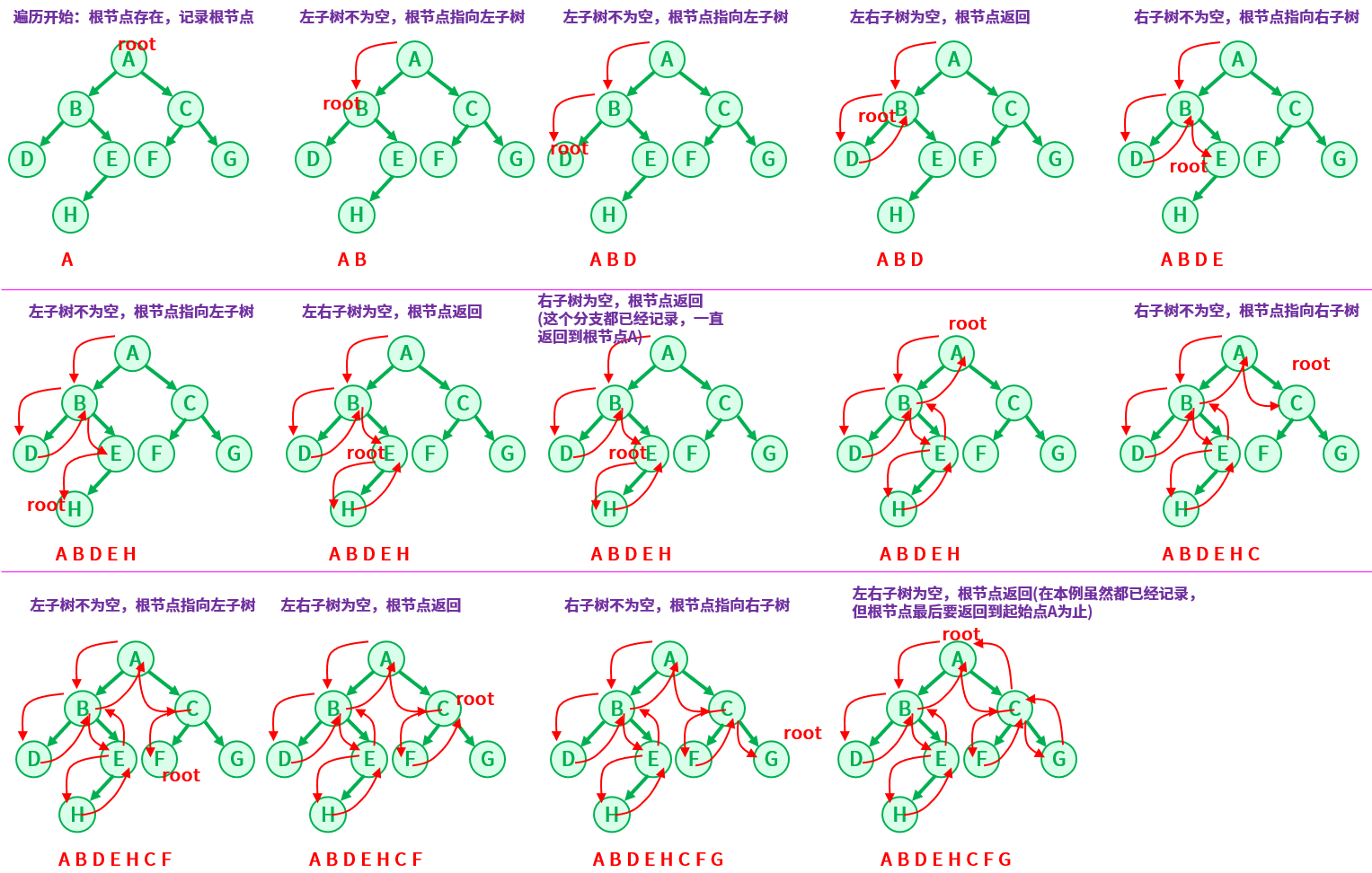
二叉树前序遍历结果是:A B D E H C F G
代码实现:
// 前序遍历--根左右
public void preOrder(TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}6.2 中序遍历
中序遍历:先访问根的左子树——>再访问根节点——>最后访问根的右子树。
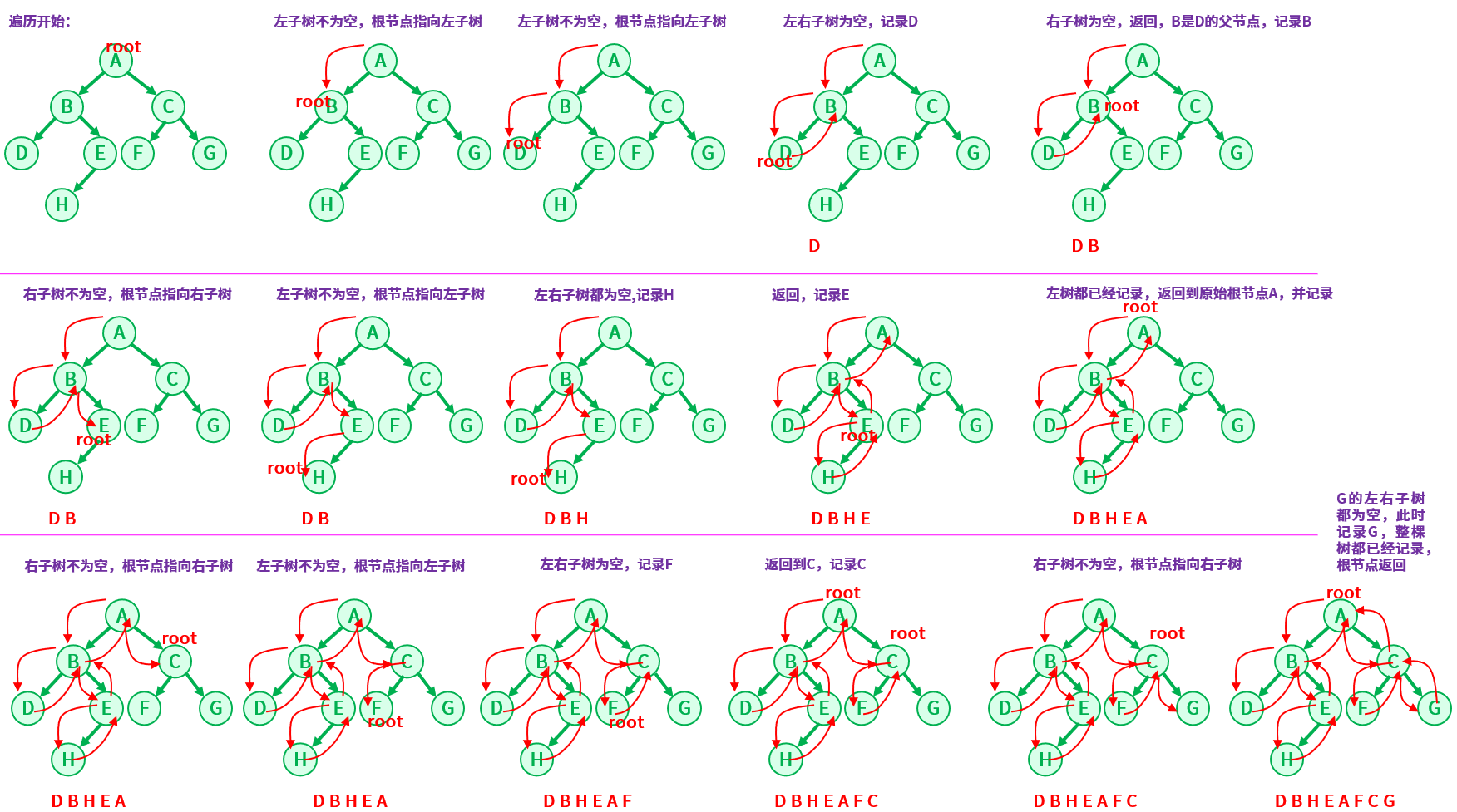
二叉树中序遍历结果:D B H E A F C G
代码实现:
// 中序遍历
public void inOrder(TreeNode root) {
if (root == null) {
return;
}
inOrder(root.left);
System.out.print(root.val+" ");
inOrder(root.right);
}6.3 后序遍历
后续遍历:先访问根的左子树——>再访问根的右子树——>最后访问根节点。
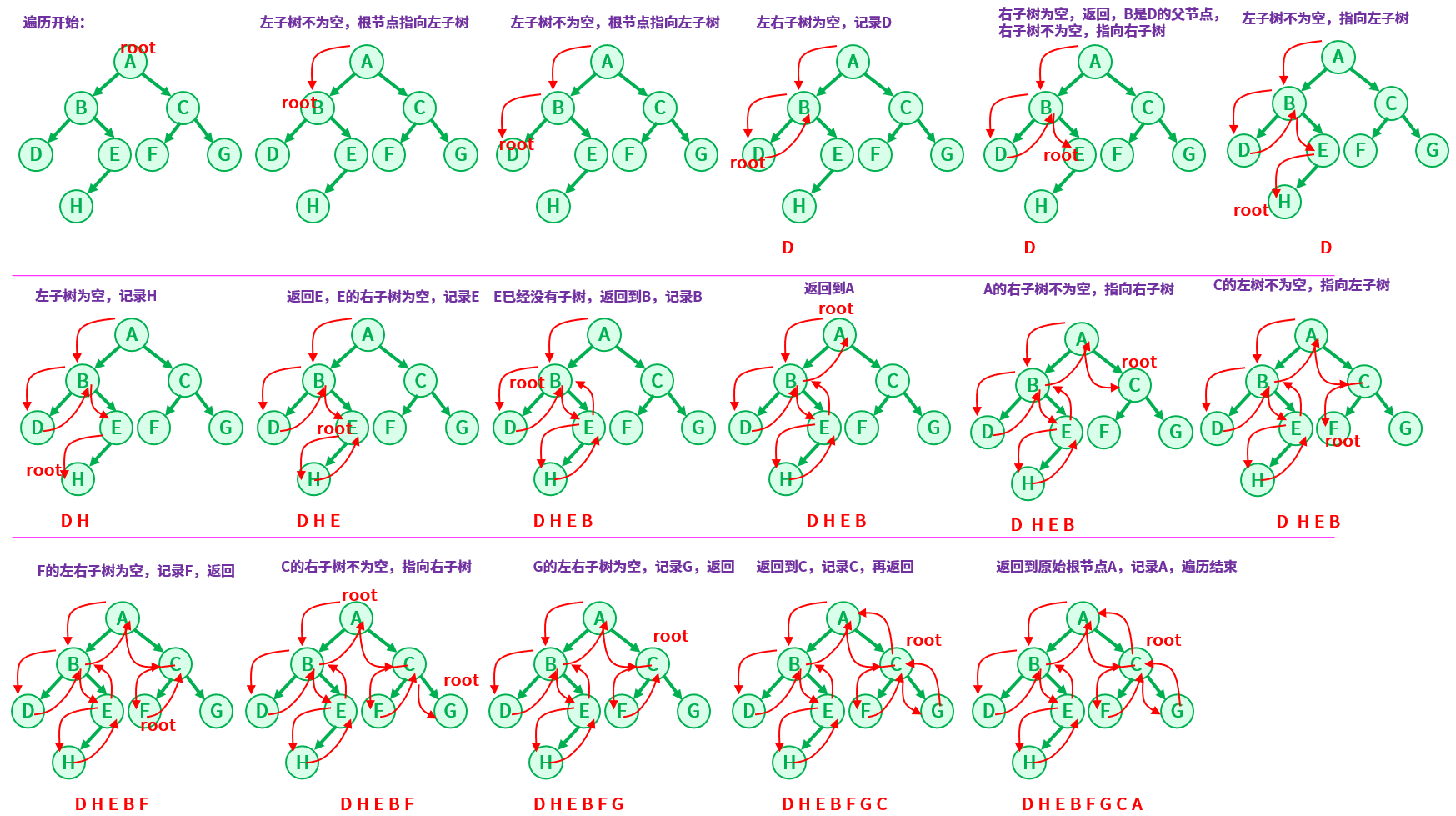
遍历结果:D H E B F G C A
代码实现:
//后序遍历
public void postOrder(TreeNode root) {
if (root == null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val+" ");
}
6.4 层序遍历
层序遍历:对二叉树的每一层依次访问,第一层访问结束再进行第二层的访问,以此类推,直至访问全部节点为止。
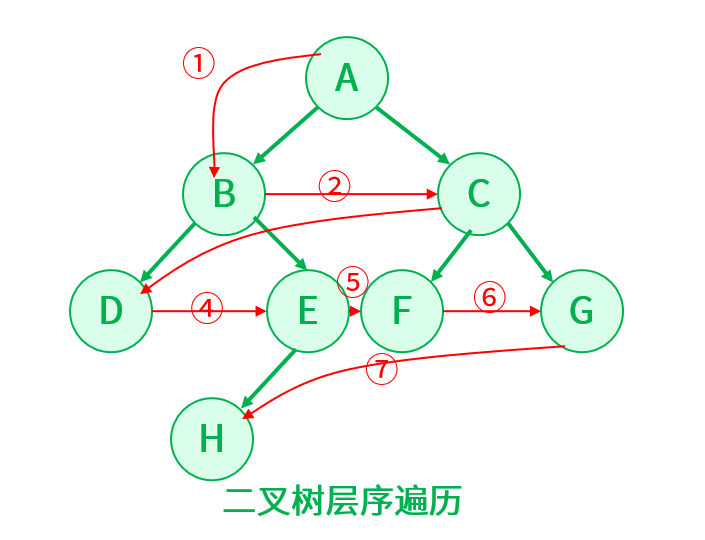
层序遍历和前面三种遍历的方式不同,因为层序遍历是一层一层地对二叉树进行访问,但是二叉树每个节点又是有左右子树的,怎么做到一层一层的访问呢?
这里就要用到队列先进先出的特性,每次处理一层的所有节点,在处理当前节点时,将其子节点加入队列。其步骤是:
将根节点放入队列
当队列不为空时:
记录当前队列大小(即当前层的节点数)
依次取出当前层的所有节点并访问
将每个节点的左右子节点(如果存在)加入队列
重复直到队列为空
以上面的图为例,开始时先让根节点 A 入队,方法 queue.offer(root),此时队列不为空,记录此时队列的大小,方法 queue.size(), 开始出队操作,方法 queue.poll(),用一个变量 cur 记录当前节点的值,出队后,判断当前节点是否拥有左右子节点,如果有,就依次将这些子节点进行入队操作,每出队一个元素,队列的大小就减 1,以此类推,直到最后一层遍历结束后,队列才会为空,遍历结束。
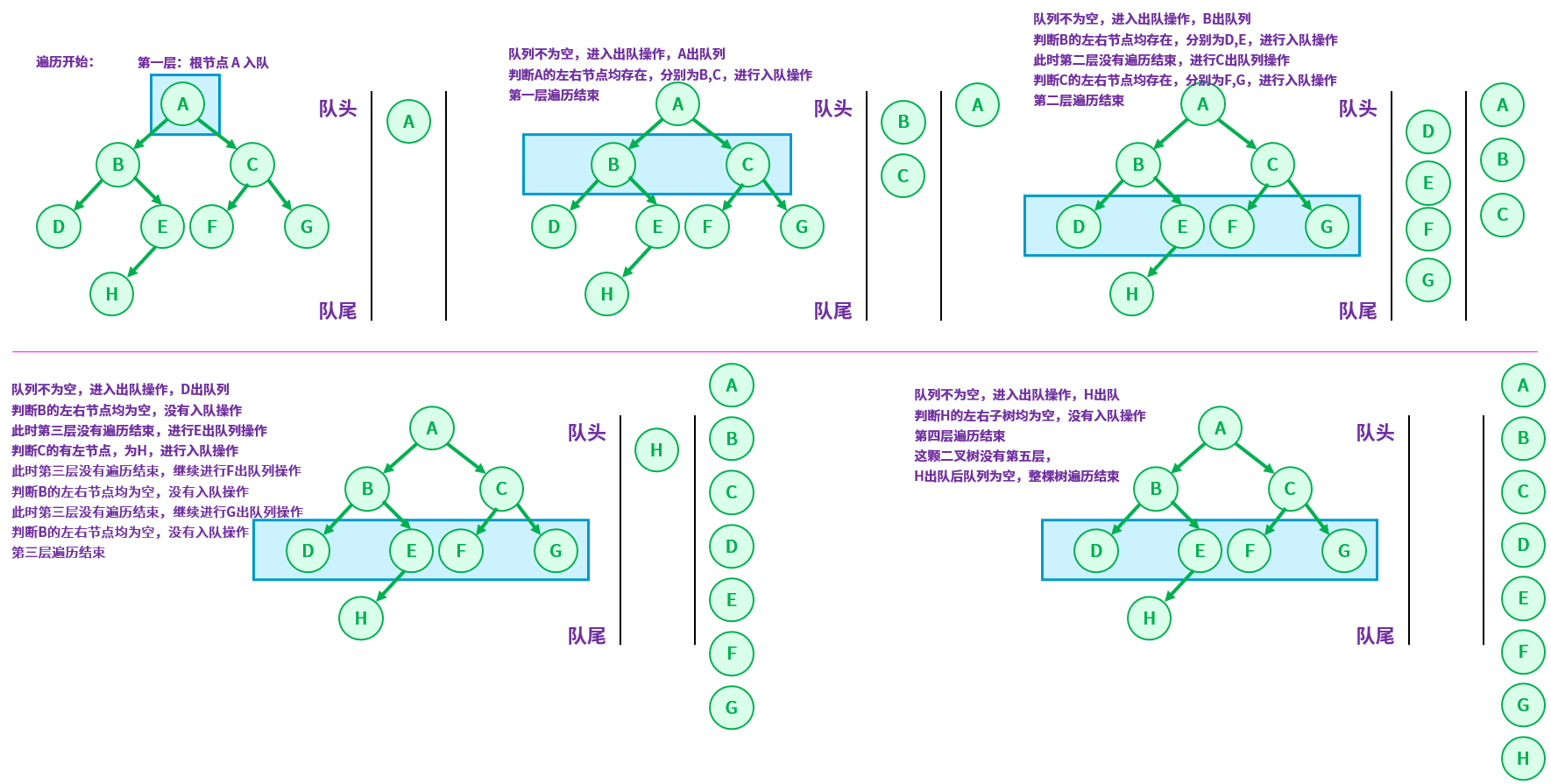
遍历结果:A B C D E F
代码实现:
//层序遍历
public void levelOrder(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (! queue.isEmpty()) {
int size = queue.size();// 记录当前层的节点数量
while(size != 0){
TreeNode cur = queue.poll();//弹出节点
System.out.print(cur.val + " ");
if (cur.left != null) {
//左节点不为空,入队
queue.offer(cur.left);
}
if (cur.right != null) {
//右节点不为空,入队
queue.offer(cur.right);
}
size--;//弹出一个节点,队列元素减 1
}
}
}
6.5 根据遍历序列创建二叉树
若只给出一棵二叉树的前序遍历、中序遍历、后序遍历、层序遍历中的一种,不能唯一确定一棵二叉树。给出两种序列(其中有一个序列必是中序遍历)才能唯一确定一棵二叉树。这是因为前序遍历、后序遍历或者层序遍历可以确定根节点的位置,而中序遍历可以确定根节点的左右子树节点数。
6.5.1 中序 + 前序
根据前序遍历的输入数组和中序遍历的输入数组创建二叉树。可以先看以下题目,作为一个了解,之后再以代码形式书写。
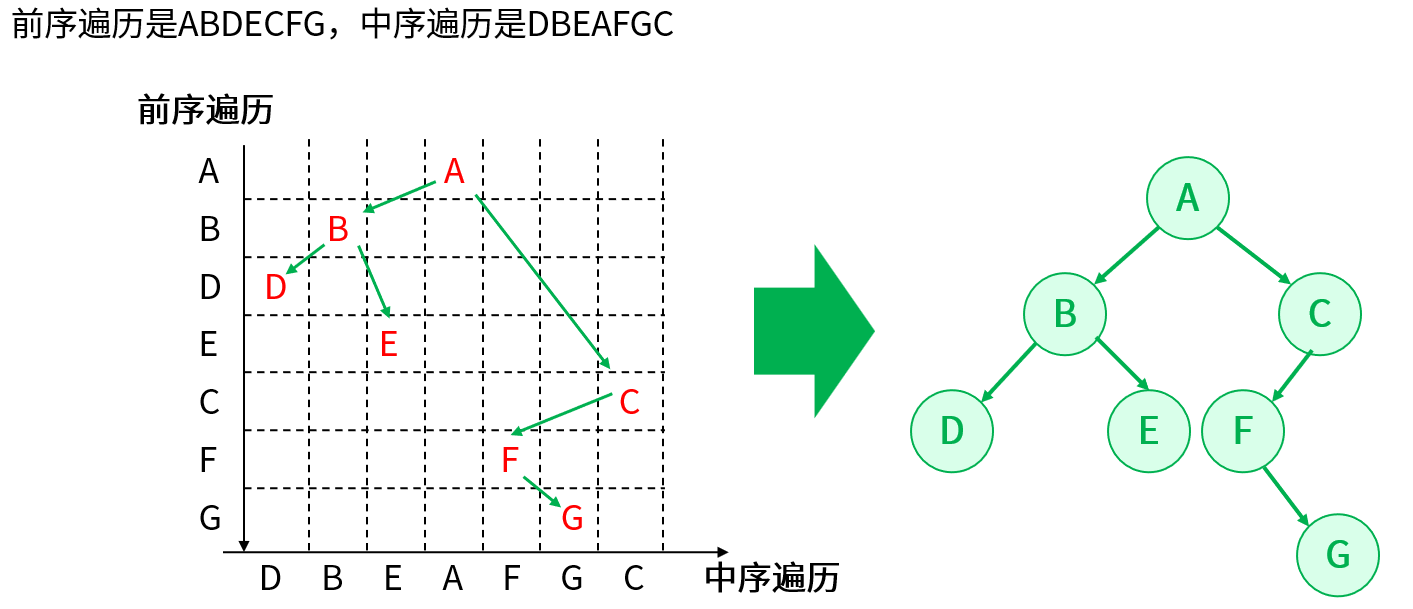
有一棵二叉树,其前序遍历是A B D E C F G,中序遍历是D B E A F G C,求其后序遍历。
解题思路:对于这个问题,想要求其后序遍历,那就要先创建一棵二叉树,然后按照后续遍历的方法求得。根据前序遍历可以知道它是从根节点开始遍历,所以根节点是A,在中序遍历中找到A,A的左边(DBE)就是它的左子树,A的右边(FGC)就是右子树;对于A的左子树,遍历的结果第一个记录是B,那么此时根节点是B,在中序遍历中找到B,B的左边是左子树,B的右边是右子树,此时在中序遍历中A的左边已经完成,即A的左子树已经完成,只剩下FGC;FGC这三个节点在前序遍历中先记录的是C,所以C是右子树的根节点,而在中序遍历中,C的左边是FG,没有右子树,所以剩下的FG,对比前序遍历和中序遍历就可以创建这棵二叉树:
所以后序遍历的结果是:D E B G FC A
图是根据解题思路的描述所画,关键在于理解前序遍历和中序遍历
根据上面的例子可以看出,如果知道了一棵树的前序遍历和中序遍历,要想还原这棵二叉树,关键点在于根据前序遍历确定根节点,根据中序遍历找到根节点确定左右子树。因为是前序遍历,根节点在第一个位置,所以确定根节点后要先创建它的左子树。详细步骤在代码中(代码是以 int 类型书写定义,如果要完成以上例子的代码,改变数据类型即可):
//根据前序遍历和中序遍历构建二叉树
private int preIndex; // 跟踪前序遍历的当前进度(指向下一个待处理的根节点)
/**
* @param preorder 前序遍历数组(根→左→右)
* @param inorder 中序遍历数组(左→根→右)
* @return 重建后的二叉树根节点
*/
public TreeNode buildTree(int[] preorder, int[] inorder) {
preIndex = 0;//前序遍历的第一个节点为根节点,从第一个元素开始
// 根据前序遍历在中序遍历的范围内构建二叉树
return buildSubTree(preorder, inorder, 0, inorder.length - 1);
}
/**
* 递归构建子树
* @param preorder 前序遍历数组
* @param inorder 中序遍历数组
* @param inStart 当前子树在中序数组中的起始位置
* @param inEnd 当前子树在中序数组中的结束位置
*/
private TreeNode buildSubTree(int[] preorder, int[] inorder, int inStart, int inEnd) {
// 终止条件:左下标大于右下标
if (inStart > inEnd) {
return null;
}
// 1:从前序数组获取当前根节点(按照前序顺序依次取节点)
TreeNode root = new TreeNode(preorder[preIndex]);
// 2:在中序数组中找到当前根节点的位置
int rootIndex = findRootInInorder(inorder, inStart, inEnd, preorder[preIndex]);
preIndex++; // 移动到前序数组的下一个元素(也是下一个根节点)
// 3:递归构建左子树(必须先构建左子树)
// - 中序数组中当前根节点左侧是左子树的范围
root.left = buildSubTree(preorder, inorder, inStart, rootIndex - 1);
// 4:递归构建右子树
// - 中序数组中当前根节点右侧是右子树的范围
root.right = buildSubTree(preorder, inorder, rootIndex + 1, inEnd);
return root;//当前子树的根节点
}
/**
* 在中序数组的指定范围内查找根节点的位置
* @param inorder 中序遍历数组
* @param start 查找起始位置
* @param end 查找结束位置
* @param target 要查找的根节点值
* @throws IllegalArgumentException 如果输入不合法(未找到目标值)
*/
private int findRootInInorder(int[] inorder, int inStart, int inEnd, int target) {
for (int i = inStart; i <= inEnd; i++) {
if (inorder[i] == target) {
return i;//返回根节点位置
}
}
throw new IllegalArgumentException("无效的遍历序列输入!!!");
}6.5.2 中序 + 后序
有了根据前序遍历和中序遍历创建的二叉树的基础,那么这个问题其实也不再是问题了。同样是先看一个例题:
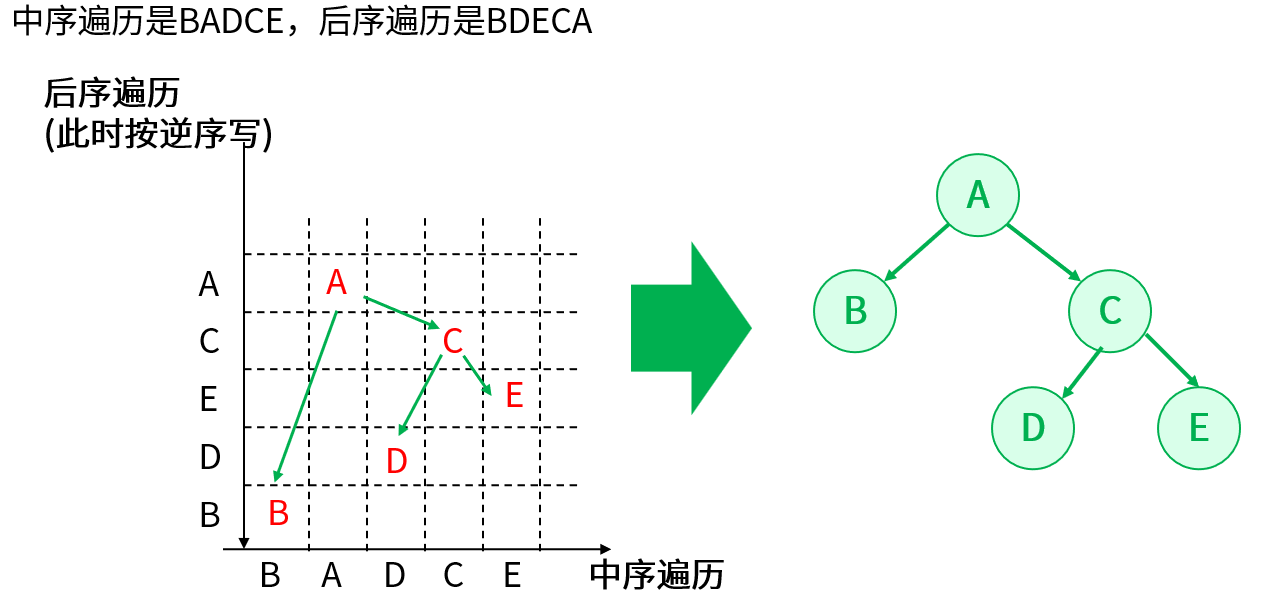
有一棵二叉树,其中序遍历是B A D C E,后序遍历是B D E C A,求其前序遍历。
解题思路:对于这个问题,想要求前序遍历,就要还原该二叉树,然后按照前序遍历的方法求得。根据后序遍历可以知道根节点是最后记录的,所以根节点是A,在中序遍历中找到A的位置,A的左边(B)就是它的左子树,A的右边(DCE)就是它的右子树;对于A的左子树只有一个节点,所以这个时候就可以确定左树;对于A的右子树,再根据后序遍历,此时得到的是C,所以C右数的根节点,回到中序遍历,就可以确定D和E分别是C的左子树和右子树,这棵二叉树全部节点创建完成:
所以前序遍历的结果是:A B C D E
根据上面的例子可以看出,如果知道了一棵树的中序遍历和后序遍历,要想还原这棵二叉树,关键点在于根据后序遍历确定根节点,根据中序遍历找到根节点确定左右子树。因为是后序遍历,根节点在最后一个位置,所以确定根节点后要先创建它的右子树。详细步骤在代码中(代码是以 int 类型书写定义,如果要完成成以上例子的代码,改变数据类型即可):
// 用于跟踪后序遍历数组当前处理的节点位置(从最后一个节点开始)
private int postIndex;
/**
* 主方法:根据中序和后序遍历构建二叉树
* @param inorder 中序遍历数组(左→根→右)
* @param postorder 后序遍历数组(左→右→根)
* @return 构建完成的二叉树根节点
*/
public TreeNode buildTree(int[] inorder, int[] postorder) {
// 最后一个节点为根节点,记录位置
postIndex = postorder.length - 1;
// 根据后序遍历在中序遍历的范围内构建二叉树
return buildSubTree(inorder, postorder, 0, inorder.length - 1);
}
/**
* 递归构建子树的核心方法
* @param inorder 中序遍历数组
* @param postorder 后序遍历数组
* @param inStart 当前子树在中序数组中的起始索引
* @param inEnd 当前子树在中序数组中的结束索引
*/
private TreeNode buildSubTree(int[] inorder, int[] postorder, int inStart, int inEnd) {
// 终止条件:左下标大于右下标
if (inStart > inEnd) {
return null;
}
// 1:从后序数组获取当前根节点(按照前序顺序依次取节点)
TreeNode root = new TreeNode(postorder[postIndex]);
// 2. 在中序数组中找到该根节点的位置
int rootIndex = findRootInInorder(inorder, inStart, inEnd, postorder[postIndex]);
postIndex--; // 移动到后序数组的前一个元素
// 注意:必须按照先右后左的顺序构建
// 3. 递归构建右子树(范围是中序数组中根节点右侧的部分)
root.right = buildSubTree(inorder, postorder, rootIndex + 1, inEnd);
// 4. 递归构建左子树(范围是中序数组中根节点左侧的部分)
root.left = buildSubTree(inorder, postorder, inStart, rootIndex - 1);
return root;
}
/**
* 在中序数组的指定范围内查找目标值的索引
* @param inorder 中序遍历数组
* @param inStart 查找起始位置
* @param inEnd 查找结束位置
* @param target 要查找的值
* @throws IllegalArgumentException 如果找不到目标值(输入不合法)
*/
private int findRootInInorder(int[] inorder, int inStart, int inEnd, int target) {
// 在当前子树范围内线性搜索
for (int i = inStart; i <= inEnd; i++) {
if (inorder[i] == target) {
return i;
}
}
// 如果找不到,说明输入的前序/中序序列不匹配
throw new IllegalArgumentException("无效的遍历序列输入!!!");
}(感谢阅读,文章较长,如有错误,还望指正!撒花❀❀❀)