线性表中的数据元素可以包括多个数据项如字符型变量项姓名、整型变量学号、指向后继的地址变量,但是线性表中的数据元素的值不能再被分,即数据元素本身不能是一个数据结构(上述学号、姓名不是一个类型的变量所以不是数据结构)。
数组和广义表就可以看成线性表在上述含义下的扩展:表中的数据元素本身也是一个数据结构。
一维数组不用多说,看作一个正常的顺序储存结构的线性表就行。二维数组可以看作数据元素是定长线性表的一维数组。由此可推广到n维数组,n维数组中含有个元素,即第1维到第n维个数连乘,如三维数组a[3][4][5]有3×4×5个元素。
多维数组的储存一般用顺序存储结构,由于存储单元是一维的结构,而多维数组是个多维的结构,则用一组连续存储单元存放数组的数据元素就有个次序约定问题。
以二维数组为列,一般是用以行序为主序,即在内存单元中排完一行再排下一行,从这里也可以看出来多维数组依旧是线性关系,是线性表的推广。
假设每个数据元素占L个存储单元,则二维数组A中任一元素的存储位置由下式确定:
LOC(i,j)=LOC(0,0)+(×i+j)L
LOC(i,j)是的存储位置,LOC(0,0)是
的存储位置,即二维数组A的起始存储位置,也称为基地址或基址。
推广到一般情况,可以得到n维数组的数据元素存储位置的计算公式
LOC(j1,j2,……jn)=LOC(0,0,……0)+(b2×……×bn×j1+b3×……×bn×j2+……+bn×+jn)L
可缩写为: LOC(j1,j2,……jn)=LOC(0,0,……0)+
其中 =L,
=
×
,1<i≤n。该式称为n维数组的映像函数。数组元素的存储位置是其下标的特性函数,一旦确定了数组的各维长度,
就是常数。由于计算各个元素存储位置的时间相等,所以存储数组中任一元素的时间也相等。我们称具有这一特点的存储结构为随机存储结构。
在数值分析中经常出现一些阶数很高的矩阵,同时矩阵中有很多值相同的元素或者是零元素。有时为了节省存储空间,对这类矩阵进行压缩存储。
- 所谓压缩存储是指:为多个值相同的元只分配一个存储空间;对零元不分配空间。
- 假若值相同的元素或者零元素在矩阵中的分布有一定的规律,则我们称此类矩阵为特殊矩阵;反之则为稀疏矩阵。
特殊矩阵
- 对称矩阵:若n阶矩阵A中的元满足下述性质
=
1≤i,j≤n,则称为n阶对称矩阵。一般以行序为主序存储其下三角(包括对角线)中的元。可以将
个元素压缩储存 n(n+1)/2,即1+2+...+n个元的空间中。
假设以sa[ n(n+1)/2]作为n阶对称矩阵A的存储结构,则sa[k]和矩阵元之间存在着一一对应的关系:
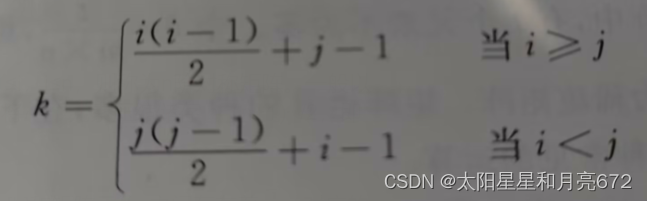
三角矩阵:所谓下(上)三角矩阵是指矩阵的上(下)三角(不包括对角线)中的元均为零的n阶矩阵。如果不是零而是一个常数C,存储方式除了和对称矩阵一样外额外储存常数C即可。
对角矩阵:所有的非零元都在以主对角线上的矩阵,如果集中在以对角线为中心的带状区域中,我们也可按以行为主或者以对角线的顺序将其压缩存储到一维数组上。