文章目录
1. 逐层伸展
1. 1 宽松平衡
曾经介绍过AVL树,这是一种典型适度平衡的二叉搜索树。你应该还记得,为此我们需要为其中的每一个节点都定义并且引入一个名为平衡因子的指标,并且要求其中所有节点的平衡因子的数值必须介于-1到+1之间。尽管相对于理想平衡而言,这种形式的适度平衡,已经在条件上略有放松,但依然显得有些过于苛刻。如果我们注意到,我们还需要在AVL树的动态调整过程中保持这种特性,这种苛刻就更是显而易见了。
如果比喻作人,AVL树就犹如那种,时时小心处处谨慎的类型,那么能否成为那类更为潇洒的人呢?也就是说,我们可否秉承一种更为宽松的准则,同时又从长远,从整体来看,依然不失某种意义的平衡性呢?答案是肯定的,答案就是我们这节的主角——伸展树。
1. 2 局部性
实际上,引入伸展树的最初动机非常的基本和原始。具体来说,也就是试图利用所谓的局部性,那么什么是局部性呢?

所谓局部性是实际的计算机环境中普遍存在的一种规律或现象。具体来说,也就是刚被访问过的数据极有可能很快的被再次访问到。
在实际的生活中,你应该也有类似的经历。比如,你有可能在机场上偶遇某位时隔五年甚至十年的老朋友,但在紧接着下来的第二天,你们或许可能又会在另一个场合,比如某个会议上在次碰面。
这样一种现象或者规律在信息处理的过程中是普遍存在屡见不鲜的。比如,我们这里讨论的BST就是一个典型的例子,对于BST来说,这一规律可以具体描述为:我们每次刚刚访问过的某一个节点都有可能很快的会再次被我们访问到,或者推而广之,我么接下来访问的那个节点即便不是你刚访问过的那个节点,也不会离它太远,所谓的虽不中,亦不远矣。
通过此前的学习,我们应该知道:对于AVL树而言,每一次查找所需的时间都是logn,因此任意的连续m次查找,所需要的累计时间无非就是O(m*logn),这无可厚非。
那么进一步的,如果我们对数据的访问的确具有上述的局部性,那么我们对数据集的访问效率能否做到更高呢?
1. 3 自适应调整
不妨来考察一个简单的实例,也就是典型的线性结构——列表。我们知道在列表结构中所有元素都按照它们之间的逻辑关系,可以排列成一个线性的序列,相邻的元素通过引用确立前驱和后继关系。
我们知道在这样的一个结构中对任何一个元素的访问效率将主要取决于它在这个序列中所具有的秩。
具体来说,秩越小,也就是越靠前的元素,访问的效率越高。秩越大,也就是越靠后的元素,访问的效率越低。
如果对于各元素的访问是完全理想随机的,我们恐怕只得如此,而不能奢望有什么实质的改进。
然而如我们刚才所说的,如果对这个集合的元素的访问具有局部性,甚至有极强的局部性,我们就可以通过简明的策略来实现对整个数据集合的更高效访问。比如一种行之有效的办法是一旦有某个元素刚刚接受访问,我们就立即将它移动到这个序列的最前端。这种技巧背后的策略不难理解。
因为根据局部性,我们接下来将要访问的元素很可能就是我们刚刚访问的那个元素,而这个元素就在此前刚刚被送到这个序列的最前端,而对于这样一个最前端的元素而言,我们的访问是唾手可得最为便捷的。
从整个数据结构的生命周期而言,这样一个列表结构,即便最初是完全随机分布的,那么在经过足够长时间的使用之后,在某一段时间内,被集中访问的那些元素都会不约而同的集中到这个列表的前端去。我们已经知道,这个区域的访问效率是相应更高的。因此我们就可以在一个足够长的时间跨度之内获得比此前更高的访问效率。
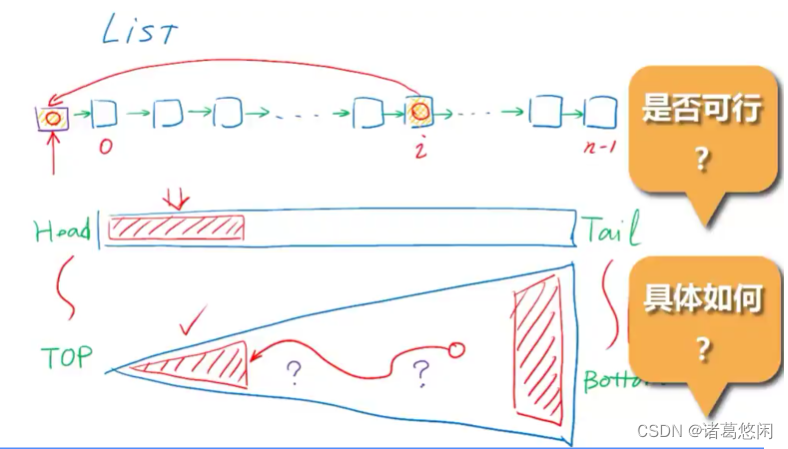
好了,现在我们可以回到我们的二叉查找树,为了便于对比,我们不妨将BST的画法旋转90度,具体来说,也就是将树的顶部和树的底部分别与列表的头部与尾部对应起来。这种对应是有道理的,因为在BST中位于顶部的元素相对于位于其他位置,尤其是底部的元素而言访问效率要高得多。因此如果我们希望借助局部性对BST的访问效率做进一步的优化,就不妨参照列表的这种技巧,将在某一段时间内,经常要访问到的元素,通过某种方式尽可能的移送到更加接近树根的位置,也就是等效的说,要尽可能的降低他们的深度。
那么这样一种构思是否真正的可行呢?如果可行的话,具体的方法又是如何的呢?
1. 4 逐层伸展
根据刚才的分析,下一个将被访问的节点很有可能就是刚被访问的节点,因此为了提高下一次访问操作的效率,一种最直接的办法莫过于将刚被访问的那个节点直接移送到根节点的位置。因此我们就得到了一个简明的策略。
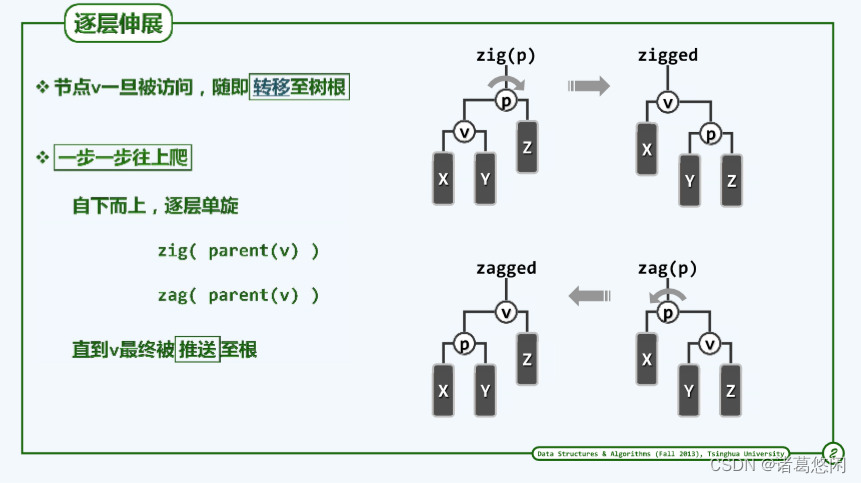
也就是说,任何一个节点,一旦被访问,我们都应随即将它转移至树根的位置。
为了实现这样一个目标,我们所能够借助的手段,依然无非是此前所介绍过的等价变换(zig zag)。
具体来说,就是zig和zag变换,如果节点V在当前这一层是左孩子,我们就通过对它的父亲做一次zig旋转,使得二者在高度上彼此互换。对称的,如果节点V当前是右孩子,就对它的父节点P做一次zag旋转,同样地,经过这样的一个调整之后,节点V和它的父亲将在高度上互换位置。
总而言之,无论是经过一次zig旋转还是zag旋转,对应的节点V都可以在高度上上升一层。
既然如此,我们不妨反复的使用这一技巧,使V的高度逐层上升,知道最终抵达树根。
1. 5 实例
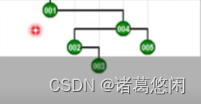
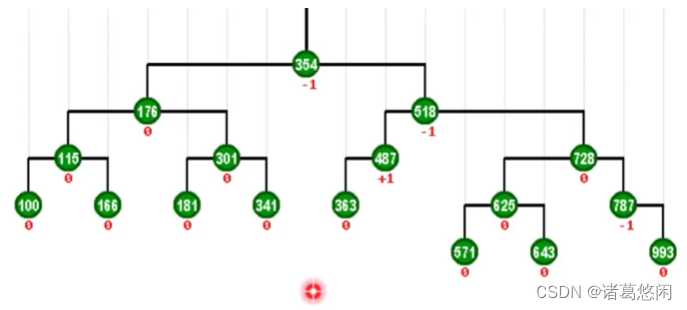
来看具体的实例,这是一棵BST。
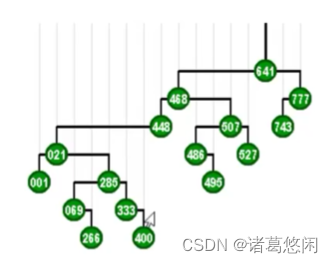
假设我们要访问333,那么按照刚才的策略,我们需要在此后通过一系列的zig和zag旋转,将它转移到树根的位置。
我们看看具体的过程
- 从333开始,首先我们注意到它是右孩子,所以要找它的父节点285并且做一个逆时针的zag旋转,这样333就上升了一层。
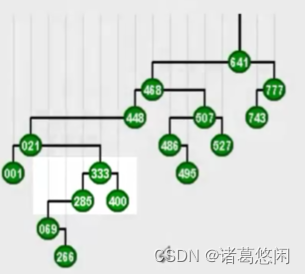
- 接下来它依然是右孩子,所以我们同样需要找到它的父亲,也就是021,并且对021做一次zag旋转,此时333已经成为一棵左孩子。
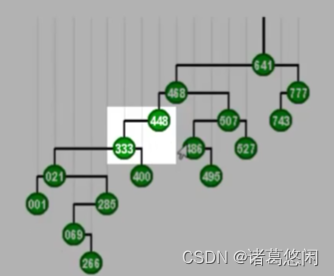
- 需要对它目前的父亲,也就是448,做一次顺时针的zig旋转,同样333的高度,因此上升一层。这个过程将继续进行下去,也就是我们进而对新的父亲468做一次相应的顺时针旋转,以及对最后一个父亲641,做一个顺时针的旋转。
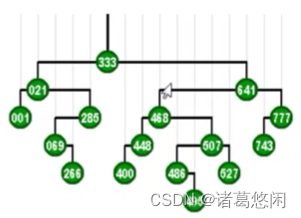
可以看到不出意外,333经过若干次zig和zag旋转的组合,最终抵达了树根。从而使得接下来对它的访问,可以几乎只需要常数的时间。如果将节点的这样一种调整过程,连贯的来看,我们就会发现,这个节点逐层上升的过程,是一个左右摇摆,不断伸展的过程,所以我们也称为这种过程为伸展 splay。
1. 6 一步一步往上爬
概括而言,对某个特定节点的伸展调整过程无非就是,自下而上,逐渐做单选调整。
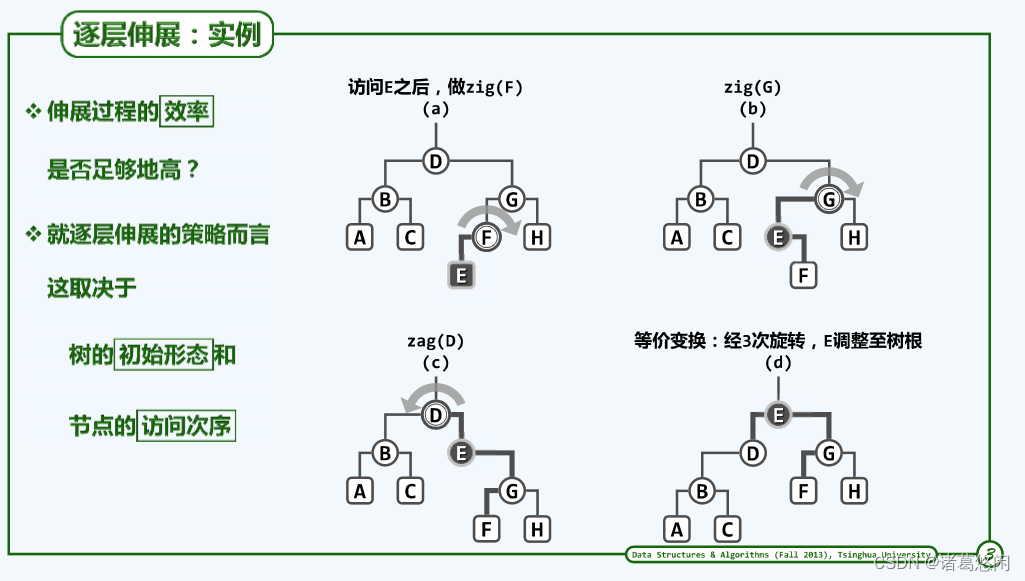
非常有意思的是,如果借用《蜗牛》那首歌中一句歌词来形容这个过程是再贴切不过的了,在这首歌里,我们会唱到,我要一步一步往上爬,描述的难道不正是这样一个过程嘛。
按照刚才所设定的策略,也就是任何节点一经访问,就随即被推送至树根,我们已经可以得到某种意义上的伸展树。
然而不幸的是,尽管蜗牛那首歌的旋律和歌词都非常优美,但是就效率而言,那句一步一步向上爬所暗示的策略,并非是最佳的选择,原因在于它有最坏情况。
1. 7 最坏情况

这棵树有do,re,mi,fa,so,la,si类似于七个音符所构成的一个逐级上升的音阶。请注意,这棵树当前的形状可以形容为是汉字中的一撇。接下来,不妨假设作为一个周期,我们就按照do,re,mi,fa,so,la,si的次序来访问这个树中的各个节点。
- 首先是do,在对它一次查找访问之后,我们将通过伸展,将它推送至树根。
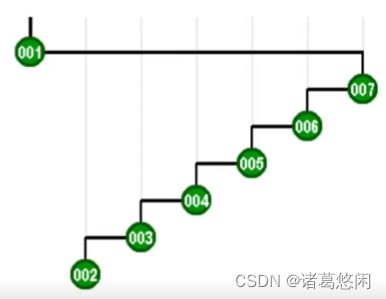
- 接下来,该轮到re,同样,在对它访问之后,我们也需要通过伸展,将它推送至树根。
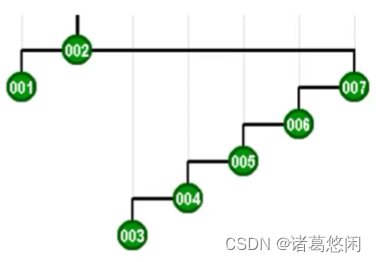
- 再接下来,该轮到是mi,同样,在对它进行访问之后,我们也需要通过伸展使之成为新的树根。
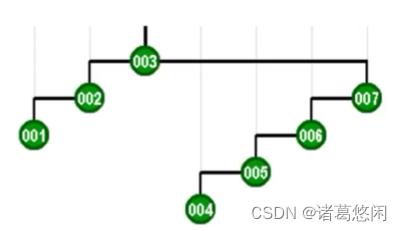
- 好,后续的过程类似,不妨直接来看下一个,以及最后的si。

请注意,经过这样一轮的访问之后,这棵树的形态,又重新的成为了汉字中的一撇。
刚才那样的访问周期,可以类似于此的一系列快照来描述
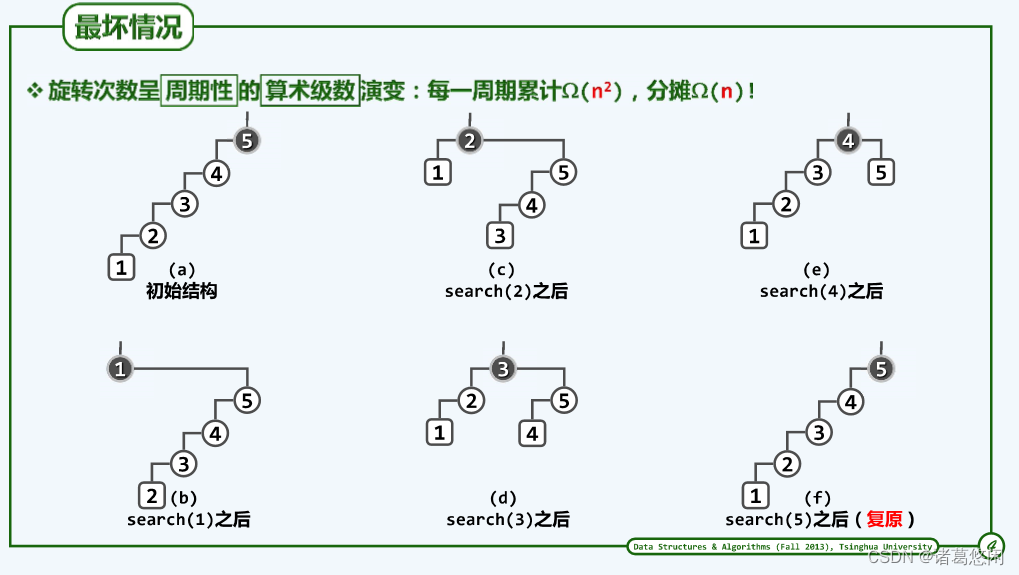
可以看到,如果这棵树的规模是n的话,那么第一个节点所需要的访问成本应该大致为n,第二个节点呢,大致为n-1,而第三个呢,是n-2,以及n-3,以及n-4,以及最终的1。
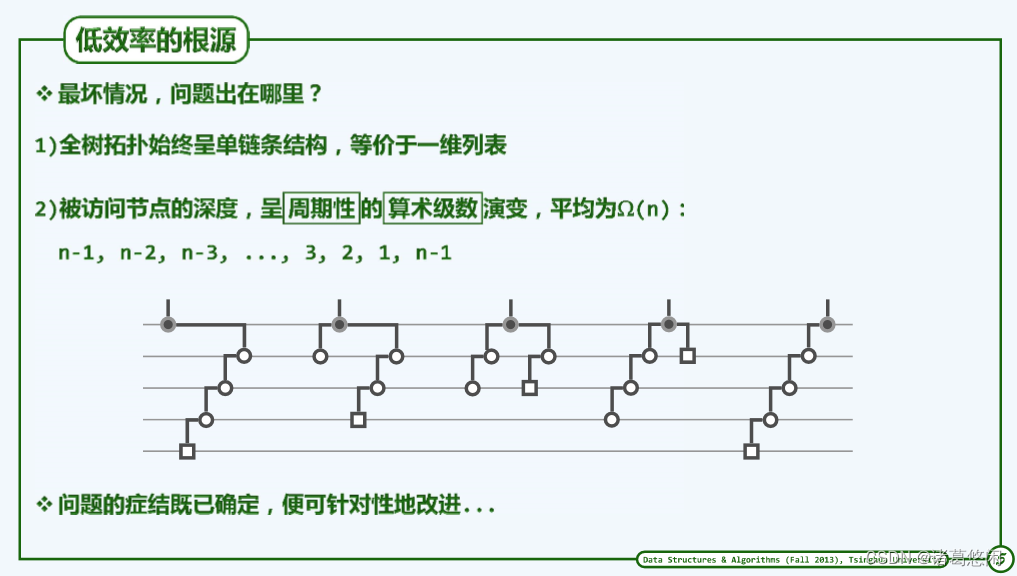
概括而言,整个周期中各自访问所对应的计算成本是按算术级数变化的,整个周期的长度为n,因此根据我们在第一章已掌握的技巧,可以推断出,整个周期内所需要的计算成本累计因该是 n 2 n^2 n2量级。如果将这个计算成本分摊到整个周期内的n次操作,我们就会发现,每次操作的分摊成本居然高达Ω(n)。
这个量不仅与AVL树的logn相去甚远,而且反过来不难发现,它已经退化成了最原始的线性序列。比如说,list或者vector的水平,因此,这样一种效率以及在背后决定这一效率的伸展策略,都是不能令我们满意的,然而好消息是问题的根源并不在于伸展本身,而是在于我们没有把它运用好。
那么我们又应该如何在原有的伸展策略基础上进行改进呢?我们马上就可以看到,从量上讲,这种改进并不大,只需要做一处非常非常微妙的改进。这就犹如画龙点睛那个故事一样,作为一条龙,我们目前的伸展策略实际上已经相当完备,它所缺乏的只是能够体现其灵魂的那样一只眼睛,没错,不是一双眼睛,而仅仅是一只。
2. 双层伸展
2.1 双层伸展
为伸展树这条龙点上那只传神之眼的是著名计算机科学家Tarjan。
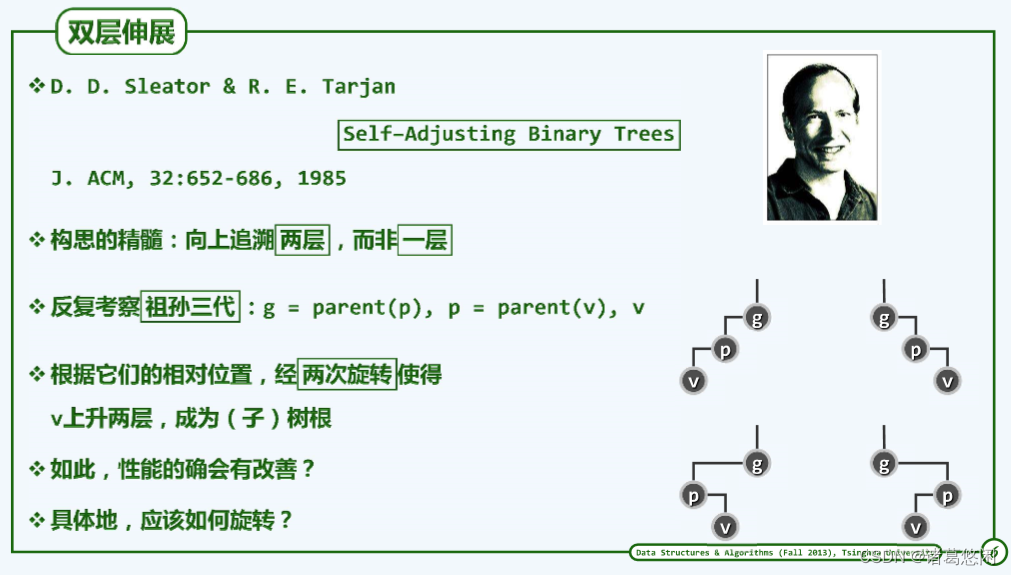
他的这一点睛之笔可以概括为不再是逐层的去进行伸展,而是将它改变为两层两层的进行。
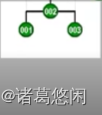
具体来说,我们需要反复考察,当前正在伸展的节点V、它的父亲p以及祖父g,并且根据这祖孙三代的相对位置,经过至多两次旋转,使得V能够一次性的上升两层。当然,他们可能的相对位置无非上图四种,也就是zig-zig,zag-zag,以及zig-zag和zag-zig。
2.2 子孙异侧
我们先来看所谓之字形的情况,也就是zig-zag或者是zag-zig。
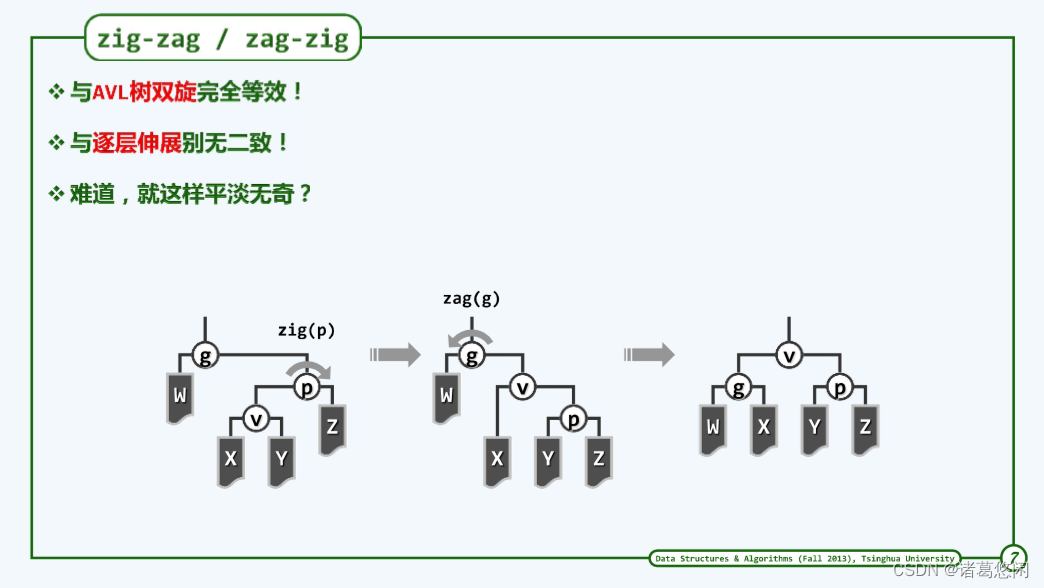
比如上图(左一)就是一种,具体来说,节点V是左孩子,而他的父亲p却是右孩子。此时,我们的改进策略是:
- 首先围绕着节点p做一次顺时针的旋转,从而得到上图(中间)状态,可以看到,v确实上升了一层。
- 接下来,我们再进而围绕着此前的祖父g做一次逆时针的zag旋转,从而将这一局部子树转化为这样一种拓扑结构(右图)。
可以看到,最终的效果是节点v抵达了此前祖父的高度。因此,整个过程的实质调整效果可以理解为是V上升了两层。
然而经过仔细观察,细心的你或许会发现,这样一种调整方法并没有什么稀罕之处,因为它与我们此前所介绍的AVL树的双旋调整是完全等效的。一个zig再加上一个zag,无论是过程还是最终的结果。
而且进一步的对比你会发现,这样一个调整过程,实际上与刚才的逐层调整,也没有任何实质的区别。
首先对父节点做旋转,进而对祖父节点进行旋转,难道这不就是逐层伸展的另一种等效形式嘛,换汤不换药。
如果你能够观察到这些现象,那非常好,因为这的确就是事实。那条龙已经具有一只眼睛,而真正的差别在于另一只眼。
2.3 子孙同侧
实际上,那另一只神奇的眼睛只有在zig-zig或zag-zag的情况下才会发光。
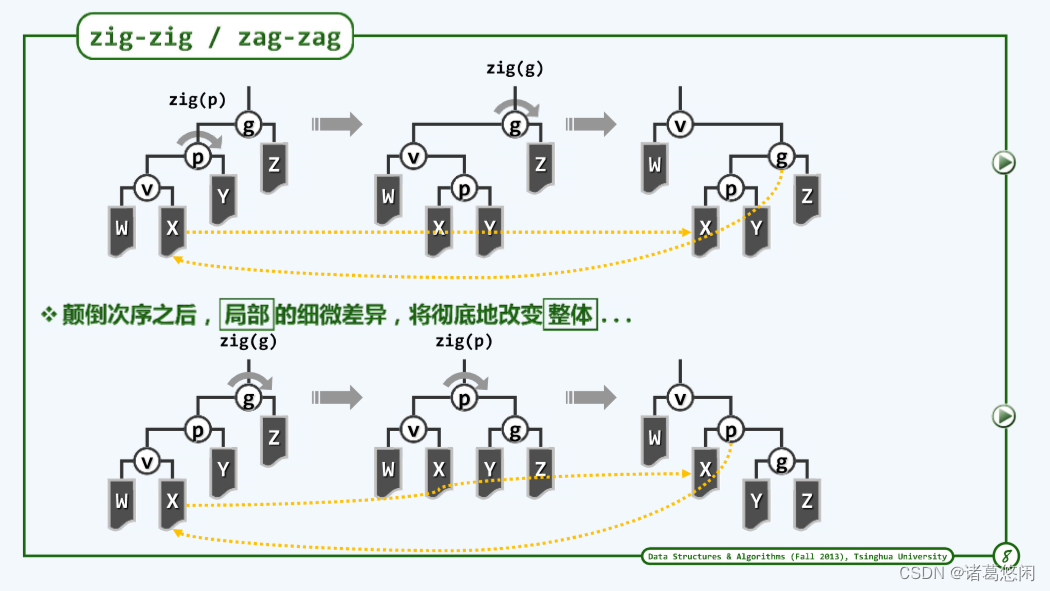
不妨只考虑其中一种,比如zig-zig情况,也就是节点v和他的父亲p都是左孩子的情况。在这里为了便于对比,不妨将这祖孙三代逐层伸展调整结果先画出来,也就是v首先经过父节点p的一次zig旋转上升一层,进而再通过祖父节点g的一次zig旋转再上升一层。我们已经对此非常熟悉,整个过程平淡无奇。我们刚才也讲过,它会导致最坏情况。
我们再来看看,Tarjan所点出的那只眼睛,或者说他所建议的调整方法。这里关键中的关键是我们需要首先越级,从祖父而不是父节点来开始旋转。
- 具体来说,经过祖父节点的一次顺时针zig旋转,节点p以及v都会上升一层。
- 接下来,进而对这棵局部子树新的树根也就是p再做一次zig顺时针旋转,从而使得v能够继续上升一层,成为这棵局部子树的树根。
将新的这种调整方法的结果与此前的逐层调整方法的结果做一对比,坦诚的讲第一次看到Tarjan为这条龙所点上的这只眼睛的时候,我并没有察觉到它有什么与众不同之处,现在你,或许也是这样,没错,各种的奥妙的确不易察觉。因为从效果来看,二者无非都是将v这个节点提升了两层而已,然而他们毕竟在局部拓扑结构上还是有微妙的差异,更重要的是,这种局部的微妙差异,将导致全局的不同,而那种不同将是根本性的,颠覆性的。
2.4 点睛之笔
为了切实的感受和领会这只眼睛的神奇之处,我们不妨来看这样一个实例。
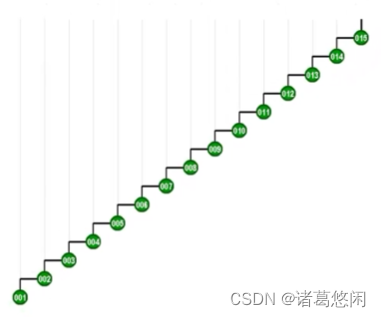
依然是汉字中的一撇,只不过为了更好的体现效果,我们这里取了更长的一撇。接下来我们不妨恶意的来访问其中最深的那个节点,因为这样的话,所消耗的时间将会最多。
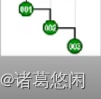
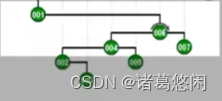
- 那么按照Tarjan建议,此时我们不仅要关心节点1的父亲,也就是2,同时也要关注它的祖父,也就是3,我们的第一次旋转,应该在祖父而不是父亲的位置上进行,因此,针对这种情况,我们首先对节点3做一次顺时针的zig。
- 接下来才轮到对原先的父亲也就是2来做一次zig,从而形成这样一种局面。v还是v,只不过上升了两层。
- 节点v,也就是001,拥有了新的一个父亲和新的一个祖父。
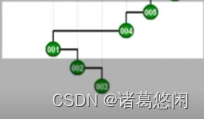
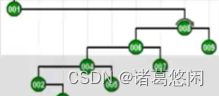
继续采用Tarjan建议的方法,具体来说,要对新的祖父也就是5做一次zig旋转。
然后再对新的这个父亲4做一次zig旋转。
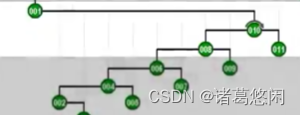
- 那么接下来继续采用Tarjan的建议,将会通过怎样的一系列双层调整,最终使目标节点1,伸展到树根呢?连续的看下这个过程。 一次双层调整
又一次双层调整
以及再一次
再一次
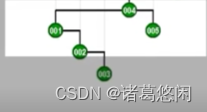
以及最终再一次,来看下最终这棵树的全貌。
看到效果了吗?不出意外,节点1被伸展到了树根,然而这只是最基本的一个任务。
我们注意到,作为这样一个调整过程的副产品,整棵树的树高已经有了本质的变化。
你应该记得,我们此前针对逐层伸展所举的那个最坏的例子。没错,那个例子之所以很坏,是因为每次尽管它能够将目标节点调整到树根,但是整棵树的高度却会不得不按照算数级数,亦步亦趋的小步的变化。于是呢?使得恶意者每次都可以去试图访问它最深的那个节点,从而导致累计的平方量级的时间复杂度,以及分摊意义上的线性时间。
而现在呢?我们至少可以看出那种恶意的方法将会失效,因为我们这棵树的形态得到了有效的优化。
具体来说,树的高度大致缩减为原先的一半,接下来如果我们继续恶意的试图去访问它的新的这个最低点,也就是003,我们就会发现,它会继续的优化调整。来看下,调整的过程以及结果。
可以看到,树的高度在此前的基础上又进而缩减了一半。
2.5 折叠效果
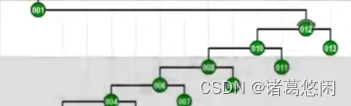
为了更好的看到树高的变化效果,我们不妨来看一棵更大的伸展树。

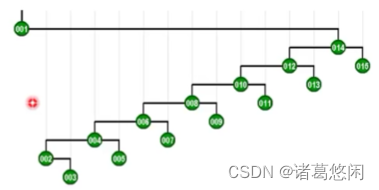
这是一棵由31个节点所构成的高度为30的伸展树。 我们继续试图恶意的来访问其中最深的也是访问成本最高的那个节点1。请留意在访问这个节点之后,对它进行的双层调整过程。尤其是观察,在每一局部,按照Tarjan所建议的方式进行调整之后,对于这棵树的整体所产生的效果。我们来看一下这棵调整之后伸展树的拓扑结构。
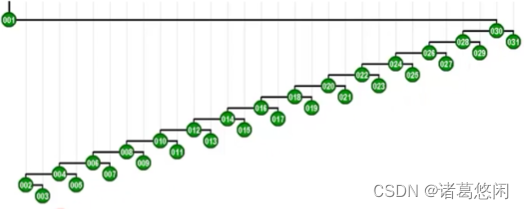
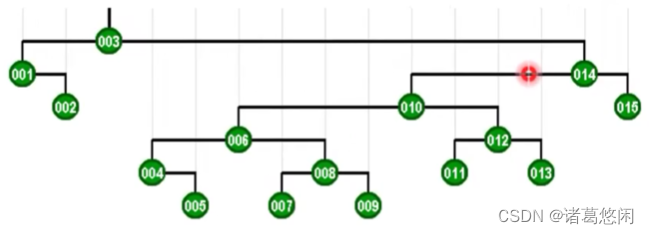
不出我们的意料,全树的高度大致也缩减了一半。接下来如果我们继续试图恶意的访问其中最深的那个节点,那么在访问完这个节点之后,将同样的通过一系列的双层伸展,将这个节点推送至树根,而且最重要的一个特性是,这棵树的高度会因此继续缩减一半。
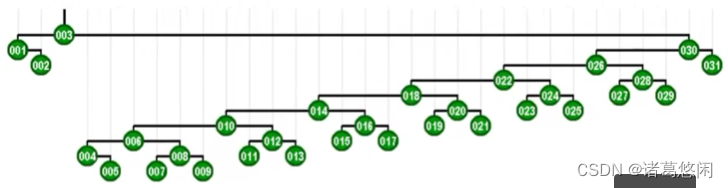
2.6 分摊性能
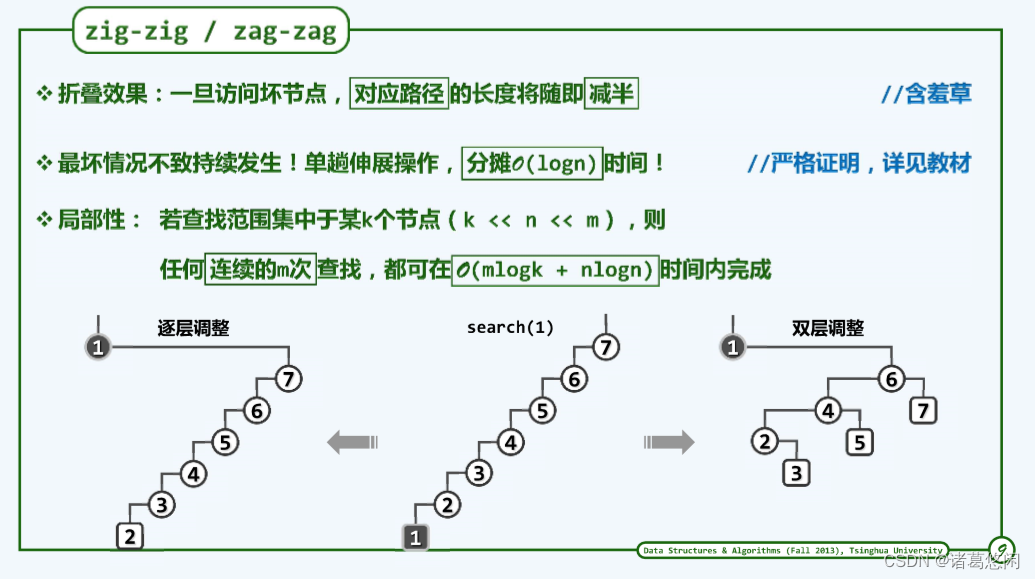
通过刚才的那个实例不难发现,Tarjan所建议的这种新方法,具有某种意义上的路径折叠效果。
具体来说,包括最坏节点在内的任何一个节点,一旦经过访问,再经过此后的双层调整之后,这个节点所对应的那条路径长度就会随即折减一半。
我们甚至可以说,这种效果具有某种意义上的智能。
既然在一棵BST中,我们非常忌讳很深的节点,那么这种折叠效果,自然就会具有对坏节点的修复作用。这就犹如含羞草那样,一旦它感受到威胁,就会通过迅速的收缩,将自己的弱点隐藏起来。
因此在采用Tarjan所建议的这种新的策略之后,刚才所举的那种最坏情况,将不至持续的发生。实际上可以严格的证明,按照新的策略,就分摊意义而言,单趟伸展操作所需要的时间都不会超过logn。
也就是说,我们现在不仅足以应对此前所涉及的那种最坏情况,而且也不会有任何其他的最坏情况,这是一个最好不过的消息了。
2.7 最后一步
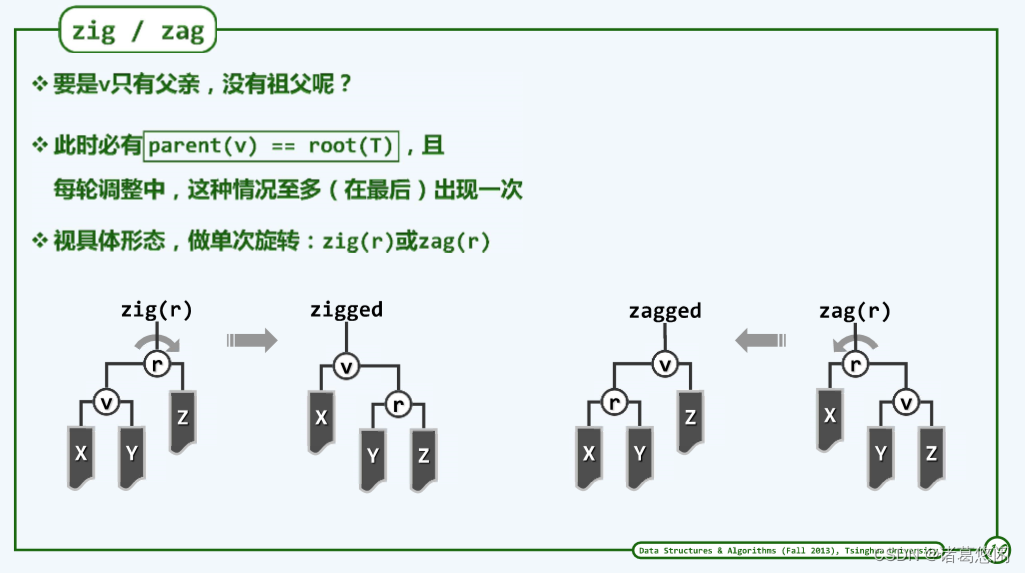
当然从完整性角度来看,还有一个细微之处需要补充。也就是如果v的深度是奇数而不是偶数,那么在最终必然会发生一种情况,也就是v只有父亲而没有祖父。此时节点v的父亲就应该是全树的根。
我们说这个问题并不严重,因为这种情况只可能在整个伸展的过程中出现一次,而且只会出现在最后。如果真出这种情况,我们就可以视具体的形态,也就是v此时究竟是左孩子还是右孩子相应的做一次zig或者是zag旋转。
既然这种情况在整个伸展的过程中只会出现一次,因此从渐进的意义而言并不会实质的影响整个调整过程的复杂度。
至此,我们应该能够理解Tarjan所建议的这种双层调整的策略不仅是完备的而且是行之有效的,那么这样一种双层调整的策略,又当如何具体实现呢?
3 算法实现
3.1 功能接口

这里再次采用模板类的形式给出伸展树的接口定义。可以看到,作为BBST的又一变种,它自然可以在我们此前已经设计并实现的BST类的基础上通过派生直接得到。
具体的与AVL树一样,我们也需要重写其中的insert和remove这样两个动态的操作接口。而与AVL树不同的是,在这里我们还需要重写search接口。
回顾一下,在其他的众多变种中,search接口都可以视作是静态的,也就是说,它并不会导致树中节点之间拓扑连接关系的变化。然而在伸展树中,正如我们此前已经看到的,这是个例外。即便是查找操作,也会引起全树的结构变化,因此,这个接口在这里也需要重写。
然而正如我们马上就要看到的,这个接口对于伸展树而言举足轻重。这个接口内部的实质功能无非是完成伸展,因此在这里我们也设计并提供了一个保护类型的splay接口,用以实现这个功能。
3.2 伸展算法
这个居于核心位置的伸展功能,大致可以实现如下。

其原理如此前我们所介绍的。
- 首先要确定待伸展的节点V,以及它的父节点p和祖父节点g,只要二者同时存在,我们就要执行一次双层调整。
- 具体来说无非是分4种情况分别处理。这4种情况,可以通过嵌套的两重if-else判断来加以识别。比如,如果我们判定V是左孩子,那我们就知道,应该属于zig类型,那么至于是zig-zig或者是zig-zag,只需在进而检查父节点是左右孩子。相应我们还可以区分zag-zag和zag-zig。
- 每经过一次双层伸展,我们都需要将局部的这棵新的子树接入到原树中对应的位置,并且更新相应节点的高度信息。
- 在所有的双层伸展都已完成之后,如我们刚才所言,还有可能要执行一次单层的调整,直至最终,整个伸展得以完成。而V呢,顺利的成为了新的树根。因此,我们也需要对这个树根做以标识。
那么这里所分出的4种情况,又当如何具体的分别应对呢?
3.3 四种情况

我们不妨来看其中的一种,也就是zig-zig的情况。
你应该记得,在这种情况下,v以及p都是左孩子。我们也知道,按照Tarjan的策略,应该就局部这棵子树(上左图)调整为这个样子(上右图)。具体来说,也就是g将成为p的右孩子,而p要成为v的右孩子。
~
请注意,这样的变换依然是一个等价变换,局部的这3个节点,以及他们下属的4棵对应的子树,在中序遍历意义上的次序将保持不变。将他们沿垂直方向都投影到水平线上,就可以验证这一点。
这里采用的方法与此前的3+4重构非常类似,我们不妨忽略具体的旋转过程,而代之以直接拼接的方式。
- 也就是说,我们需要将p的右孩子当作g的左孩子。这个效果可以由这一句
attachAsLChild(g,p->rc)完成。 - 那么下一句
attachAsLChild(p,v->rc)呢?它的作用是将v的右孩子,也就是这个X转作p的左孩子。 - 而这一句
attachAsRChild(p,g)呢?其效果是将g作为p的右孩子。 - 而最后这句
attachAsRChild(v,p)的效果雷同。
类外的3种情况与上述雷同。
3.4 查找算法
再看伸展树的查找接口应当如何实现,这里给出一种可能的实现方法。

首先与常规的BST一样,也需要调用searchIn这个接口,在以root为根的BST中,查找数值为e的节点。
我们知道,查找可能成功,也可能不成功。
- 如果查找成功,我们就需要随即将命中的节点p,通过刚刚介绍的splay算法伸展至树根,并且将命中的节点,也就是树根返回。
- 如果是失败的情况呢?虽然没有命中的节点,但是我们知道会有一个搜索路径的终点_hot,在这里,我们也将这个终点通过splay算法伸展至树根。
所以概括而言,无论是成功或者失败,我们都会在树根处获得一个相等或者近似的节点,不难理解这种处理手法的原理正是为了充分利用我们此前所介绍的局部性。需要强调的是,既然在内部需要调用splay算法调整树的拓扑结构,所以对于伸展树而言,search接口将不再是一个静态的操作。这也是伸展树区别其他同类BBST的最本质特点。
那么伸展树的另外两个动态接口,也就是insert和remove又当如何实现呢?
3.5 插入算法
先来考察插入算法。

按照直观的思维,调用BST标准的插入算法,然后再按照伸展树的规则,将新节点伸展至树根的位置。
然而我们发现,这种实现方法在这里显得过于迂回曲折。
因为无论如何在真正实施插入操作之前,我们必然已经调用过一次search接口,而我们刚刚也已重写过的search接口,实际上已经集成了一个splay操作。也就是说,即便查找可能失败,在此之后,根节点也必然是_hot节点。
你应该记得,我们的新节点本来就应该作为_hot的左或右孩子接入树中的,既然_hot已经在根节点处唾手可得,我们为什么还要费尽周折的去做更复杂的操作呢?沿着这一思路,我们不妨按照上面这种图给出的流程,来完成伸展树的插入算法。
- 具体来说,首先调用重写之后的search接口,而且不失一般性,我们的查找是失败的,并且记失败前最终的节点为t,也就是我们此前所说的_hot。
- 接下来,集成在search接口内部的那个splay操作,自然会将这个_hot推送至树根位置,如这个图所示(左二)。
- 接下来,我们不妨从逻辑上,将整棵树在t这个位置上一分为二,比如将 t 与它的右子树分离开。
- 接下来,我们可以引入节点v,并且将t以及它的后代作为V的左子树,而原先从t处分离出来的右子树呢?将作为v的右子树,重新接入这棵树中。
纵观整个过程以及最终的结果,我们不难发现,其效果与通常的插入完全一样。具体来说,不仅使得一个新节点得以顺利插入树中,而且同样使它处于树根的位置,就像它曾经被推送上去。
3.6 删除算法
再考察节点删除算法

同样的,按照直观的思维,我们或许会首先按照BST的标准删除算法实施删除,再按照伸展树的约定,将与之领进的节点,比如_hot伸展到树根的位置。同样的,这种方法本来也无可厚非,但是在此时,也依然显得有些迂回。
这背后的原因也是类似的,因为不失一般性,如果在删除操作之前的search操作是成功的,那么在查找之后,待删除的目标节点必然已经被推送到了树根的位置。既然如此,我们为何不随即就在树根的位置附近来完成这样一次删除操作呢?具体过程如上图所示。
- 同样的,我们也需要经过一次查找,对待删除的节点进行定位,而且不失一般性,不妨假设成功。
- 于是在紧随其后集成在search接口内的伸展操作之后,这个待删除节点自然也就会被伸展并推送到树根。
- 接下来呢?既然他就是待删除的元素,我不妨将这个节点释放。
于是从逻辑上看这个节点的左右子树就变得彼此分离,剩下的任务是,如何将他们重新合并起来。这里有很多种方法。
- 比如可以在右子树中找到一个最小的节点(如果你一时还想不起如何才能找到这个节点,那么我的建议是不妨回过头看一看此前所介绍的中序遍历算法迭代版)。关于这样一个节点,我们不难发现,尽管它是右子树中最小者,相对于左子树来说,它却应该是最大者。
- 因此接下来,只要将原先的左子树作为这个节点的左子树连接上去,就不仅可以完成拓扑结构上的连接,而且能够保持所有元素的中序遍历次序,也就是说我们顺利的将他们合二为一了。
而这样一个过程的整体效果呢?同样是我们所期望的,具体来说,所需要的删除的节点确实被删除了 ,而且在此之后,作为树根的节点,是一个与此前那个节点非常临近的一个。也就是说,在此后局部性将可以继续得到充分的利用。
3.7 综合评价
最后我们来对伸展树的性能和特点做一个综合的回顾。

首先需要再次强调的是相对此前的AVL树,伸展树显得更为灵活和变通,它不需要再记录节点的高度或者平衡因子之类的附加信息,因此从编程实现的角度来看会更为简便易行。而另一方面,就时间复杂度而言,依然可以确保是在logn的范围内,这也与此前的AVL树相当。
请注意,这样一个复杂度界限并没有任何更多的先决条件,包括我们最初所介绍的局部性条件。
事实上,当局部性存在的时候,伸展树的性能还会更高。
不妨考虑一种极端的情况,也就是局部性非常强的时候,在这个时候,即便数据集的规模能够达到n,在相当长的一段时间之内,我们所访问的数据可能只是其中很少的一部分,比如只有远远小于n的k个,而我们的操作次数呢?却要远远大于n。
~
比如你用电脑的过程往往就是这样,尽管你的硬盘上所存放的数据文件等等是数以万计甚至几百万计,但是在很短时间内,你所经常使用的数据往往只是其中非常低的一个百分比。比如当你在online上苦苦做题的几天之内,你所访问的数据很可能是你的硬盘中屈指可数的那么几个文件,是不是。
~
也就是说,这类情况的特点,可以概括为尽管我们所存放的数据非常的多,但是在相当长的时间内,我们所访问的只是其中非常小的一部分,如果我们把这个数据集组织为一棵BST,并且采用伸展树的策略进行自我调整,那么可想而知的是,经过一段时间的使用之后,我们最常用的那部分数据都会逐步的集中到树根的附近,以至于其他部分的数据几乎可以忽略掉,他们存在与否,已经不甚重要了,也就是说,我们完全可以认为数据集无非就是一个规模为k而不是n的一棵BBST。
~
这样一棵规模为k的BBST其访问的效率自然就应该接近于每次是logk而不是logn。因此对于任何一个足够长的操作序列而言,其中每一次操作的均摊时间复杂度也就大致是logk,当然在达到这种状态之前,我们大致要经过常规的n次操作,每次操作的时间复杂度是logn。
~
你使用电脑的经历也应该能够验证这样一个规律,难道不是吗?你的每一台新安装的电脑,不都是在经过一段时间的应用之后,就会变得非常顺手,使得在接下来的足够长的时间之内都能够飞速的运转。是的,这是因为通常的操作系统都充分利用了数据访问的局部性,从而使得缓存的命中率能够达到经可能的高。
当然,尽管具有以上诸多优点,我们不得不说,伸展树也并非十全十美,比如尽管它的分摊效率很好,但它依然不能够保证杜绝单次最坏情况的出现。
实际上,在此前已经看到伸展树的形状在任何时刻通常都是不平衡,甚至是极其不平衡。
因此我们完全可能在某一个不幸的时刻需要访问一个足够深甚至是最深的节点。尽管伸展树在此后会随即将这条路径缩短近一半,但是在此前的这次查找过程中你不得不仍需付出沉重的代价。因此在对单次操作效率十分敏感的场合,伸展树依然是不能适用和胜任的。
这类例子虽然不多,但也的确存在,比如在手术室里,控制手术器械的程序断乎不能采用伸展树这一类的数据结构。
当然也正如我们所看到的伸展树的复杂度分析是一个非常复杂的课题,在这里我们只是以形象的方式通过举例进行了一定的验证,而严格的证明却要更加复杂。