使用Python绘制二项分布的概率质量函数(PMF)
在这篇博客中,我们将探讨如何使用Python中的scipy库和matplotlib库来绘制二项分布的概率质量函数(PMF)。二项分布是统计学中常见的离散概率分布,描述了在固定次数的独立试验中,成功次数的分布情况。
代码示例
以下是一个完整的代码示例,展示了如何绘制二项分布的PMF:
from scipy.stats import binom
import pylab as plt
# 定义二项分布的参数
n = 6 # 试验次数
p = 0.3 # 成功概率
# 生成可能的成功次数
x = plt.arange(7) # 0到6的整数
y = binom.pmf(x, n, p) # 计算每个成功次数的概率
# 创建第一个子图:竖线图
plt.subplot(121)
plt.plot(x, y, 'ro') # 绘制红色圆点
plt.vlines(x, 0, y, 'k', lw=2, alpha=0.5) # 绘制竖线
plt.xlabel('成功次数')
plt.ylabel('概率')
plt.title('竖线图')
# 创建第二个子图:茎叶图
plt.subplot(122)
plt.stem(x, y, use_line_collection=True) # 绘制茎叶图
plt.xlabel('成功次数')
plt.ylabel('概率')
plt.title('茎叶图')
# 保存图像并显示
plt.savefig("figure9_2.png", dpi=500)
plt.show()
代码解释
导入库:
from scipy.stats import binom import pylab as plt我们导入了
scipy.stats中的binom模块来处理二项分布,并导入pylab作为绘图工具。定义参数:
n = 6 # 试验次数 p = 0.3 # 成功概率这里我们定义了二项分布的参数:试验次数
n和成功概率p。生成数据:
x = plt.arange(7) # 0到6的整数 y = binom.pmf(x, n, p) # 计算每个成功次数的概率我们生成了可能的成功次数
x(从0到6),并计算了每个成功次数的概率y。绘制竖线图:
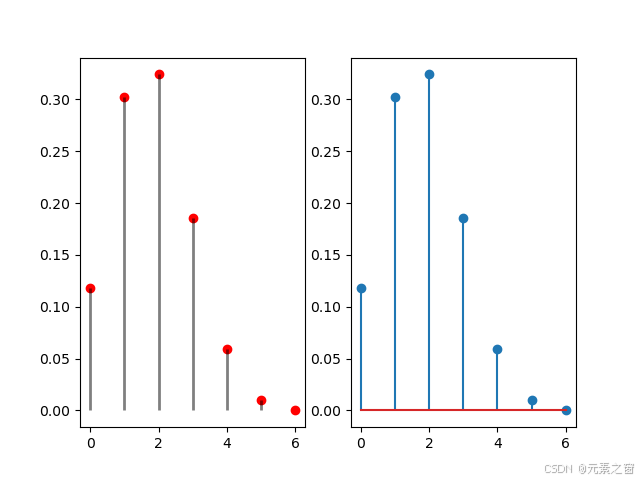
plt.subplot(121) plt.plot(x, y, 'ro') # 绘制红色圆点 plt.vlines(x, 0, y, 'k', lw=2, alpha=0.5) # 绘制竖线 plt.xlabel('成功次数') plt.ylabel('概率') plt.title('竖线图')在第一个子图中,我们绘制了竖线图,使用红色圆点表示每个成功次数的概率,并用黑色竖线从x轴延伸到每个点。
绘制茎叶图:
plt.subplot(122) plt.stem(x, y, use_line_collection=True) # 绘制茎叶图 plt.xlabel('成功次数') plt.ylabel('概率') plt.title('茎叶图')在第二个子图中,我们绘制了茎叶图,使用竖线和圆点来表示每个成功次数的概率。
保存并显示图像:
plt.savefig("figure9_2.png", dpi=500) plt.show()最后,我们将图像保存为高分辨率的PNG文件,并显示图像。
总结
通过这篇博客,我们学习了如何使用Python绘制二项分布的概率质量函数(PMF)。我们使用了scipy库来计算二项分布的概率,并使用matplotlib库绘制了竖线图和茎叶图。这些图表可以帮助我们更好地理解二项分布的特性和行为。
希望这篇博客对你有所帮助!如果你有任何问题或建议,欢迎在评论区留言。谢谢阅读!