堆
堆(Heap)是一种特殊的完全二叉树数据结构,满足以下特性:
1.完全二叉树:堆是一棵完全二叉树,即除最后一层外,其他层的节点都被元素填满,且最后一层的节点尽可能地从左到右排列。
2.堆序性质:在最大堆中,每个节点的值都大于或等于其子节点的值;在最小堆中,每个节点的值都小于或等于其子节点的值。
堆通常通过数组来实现,因为完全二叉树可以高效地映射到数组中。
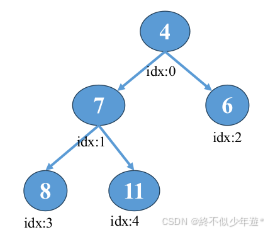
在数组表示中,假设根节点存储在数组的第一个位置(索引为0),对于任意一个节点,其父节点和子节点的位置可以通过以下公式计算:
父节点索引:parent(i) = (i - 1) // 2
左子节点索引:left(i) = 2 * i + 1
右子节点索引:right(i) = 2 * i + 2
堆的常见操作包括:
1.插入元素:将新元素添加到堆中,并通过上浮操作(sift up)维护堆的性质。
2.删除堆顶元素:移除堆顶元素(最大堆的最大值或最小堆的最小值),并通过下沉操作(sift down)重新平衡堆。
3.构建堆:将无序数组转换为堆结构,常用的方法是从最后一个非叶子节点开始,依次对每个节点进行下沉操作。
eg:
使用list表示一个堆
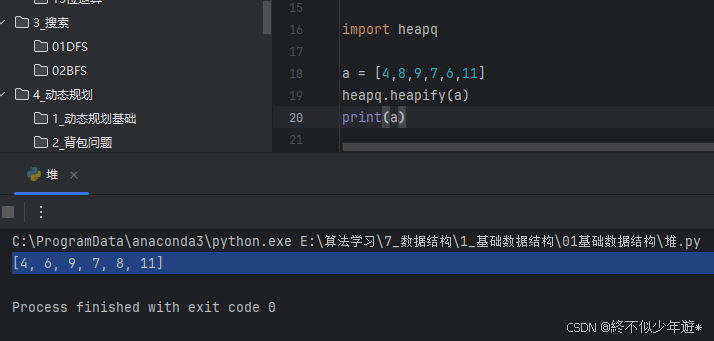
1.将无序List转换成最小堆:
heapq.heapify(a)
2.最小堆a中添加元素x:
heapq.heappush(a, x)
3.弹出并返回最小元素:
heapq.heappop(a)
4.弹出并返回最小元素,同时添加元素x:
heapq.heapreplace(a, x)
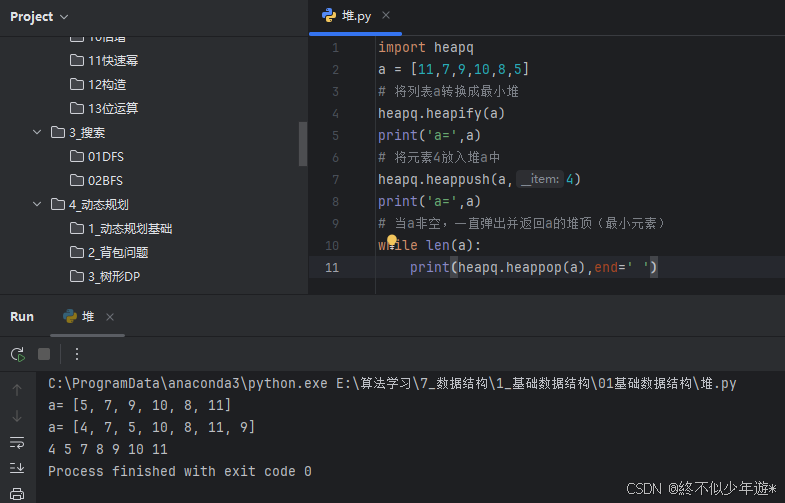
import heapq
a = [11,7,9,10,8,5]
# 将列表a转换成最小堆
heapq.heapify(a)
print('a=',a)
# 将元素4放入堆a中
heapq.heappush(a,4)
print('a=',a)
# 当a非空,一直弹出并返回a的堆顶(最小元素)
while len(a):
print(heapq.heappop(a),end=' ')
代码例子中,往a中添加元素4的过程:

删除最小元素的过程:
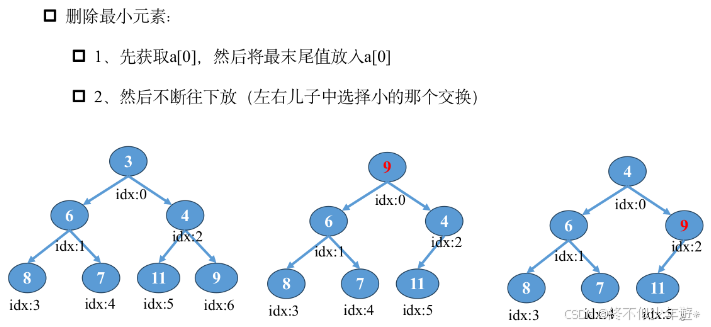
注意:图中元素9和元素6还要进行换位,然后9再和8换位,输出的堆以序列的形式呈现[4,8,9,7,6,11]
堆在计算机科学中有广泛的应用,例如:
优先队列:使用堆实现的优先队列可以高效地获取和删除优先级最高的元素。
堆排序:利用堆的性质对数组进行排序,时间复杂度为O(n log n)。
图算法:在Dijkstra算法等图算法中,堆用于快速获取当前最短路径的节点。
优先队列
优先队列(Priority Queue)是一种特殊的队列数据结构,其中每个元素都关联有一个优先级。与传统的先进先出(FIFO)队列不同,优先队列总是优先处理优先级最高的元素。
主要特点:
元素出队顺序:每次出队操作都会移除并返回当前优先级最高的元素。
实现方式:优先队列通常使用堆(Heap)数据结构实现,最常见的是二叉堆。在二叉堆中,最小堆用于实现最小优先队列,最大堆用于实现最大优先队列。
一般我们使用优先队列采用queue库中的PriorityQueue
定义优先队列:
from queue import PriorityQueue
pq =PriorityQueue()
元素x入队:
pq.put(3)
pq.put(2)
pq.put(1)
获取最小元素:
print(pq.queue[0])
取出最小元素:
print(pq.get())
print(pq.get())
print(pq.get())
底层实现仍然是先前的heapq
from queue import PriorityQueue
pq = PriorityQueue()
# 元素x入队
pq.put(6)
pq.put(4)
pq.put(2)
# 获取最小元素 2
print(pq.queue[0])
print(pq.queue[2]) # [2,6,4]
# 取出最小元素 2
print(pq.get())
# pq 本身无法直接通过 print(pq) 来显示其内部的队列内容,因为 PriorityQueue 是一个线程安全的类
print(pq.queue)
print(pq.get())
例题:
每一个打印任务都有其重要性,小蓝用一个 11 到 99 的数字来表示,数字越大表示这个任务越重要。复印机的运行规则如下:从待打印任务队列中取出一个任务,如果队列中还有比这个任务更重要的任务,那么就把这个任务放回队列的尾部,等待下一次打印;否则就开始打印这个任务。需要注意的是,一旦开始打印任务,就不会再把它放回打印队列。我们假设每个打印任务都需要 11 分钟才能完成。

# 涉及队列中元素的优先级 -- 优先队列
# 用一个 1到9的数字来表示,数字越大表示这个任务越重要 -- 最大堆 取负号后再放入优先队列中
from queue import Queue,PriorityQueue
# 普通队列模拟任务(先进先出),优先队列模拟‘神奇复印机’的工作方式
N,X = map(int,input().split())
# x是要确定的优先级
a = list(map(int,input().split()))
q = Queue()
pq = PriorityQueue()
# 添加任务到普通队列
for i,x in enumerate(a):
q.put((i,x))
# 取负号,维护最大堆
pq.put(-x)
wait = 0
while True:
# 模拟一开始的任务顺序
i,x = q.get()
# 最大堆堆顶,即优先级最高的‘任务’(元素)
if -x == pq.queue[0]:
pq.get()
wait += 1
# 是小桥的任务 不能写:x == a[X],因为值不一定唯一但位置是唯一的
if i == X:
print(wait)
break
# 如果这次任务不是优先级最高的任务就要放回普通任务中,否则会出现任务丢失的情况
else:
# q一直保持原长度,避免丢掉任务
q.put((i,x))