工具变量(Instrumental Variables)通俗图解:破解内生性困境的利器
在数据建模与因果推断过程中,我们经常遇到一个棘手问题:内生性(Endogeneity)。它会导致模型估计产生偏差,进而误导决策。在这篇文章中,我们将结合一幅图解,用通俗语言讲清楚什么是工具变量(Instrumental Variables, IV),它能解决什么问题,以及我们应该如何理解它的使用逻辑。
一、问题背景:内生性是什么?
先来看图中这两个变量:
抗议规模(Protest Size)
政策变化(Policy Change)
现实中我们可能想研究:“抗议规模是否会推动政策变化?” 这是一个典型的因果推断问题。但问题在于——是否存在其他因素同时影响了两者?
例如:
政府已经有改革意向 → 民众更愿意抗议 → 出现政策变化
社会舆论高涨 → 导致抗议与政策共同变化
这就造成了所谓的内生性问题。即:变量之间不是简单的单向因果,而是存在共同原因或反向因果。
二、图解工具变量法的核心思路
我们来看这张图(如下):
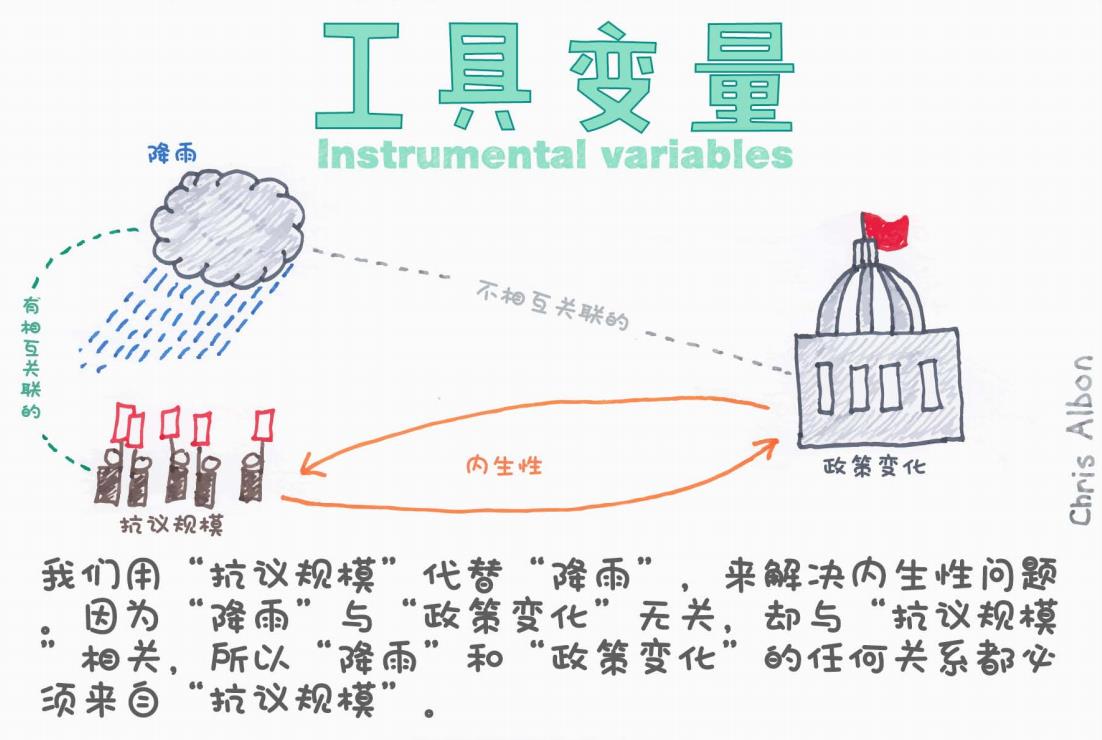
图中包含了几个重要角色:
☁️ 降雨(Rain):我们无法控制,但它却影响了抗议规模。
🧍♂️ 抗议规模:我们感兴趣的“中介变量”。
🏛️ 政策变化:我们研究的“结果变量”。
🔁 内生性:抗议规模与政策变化之间存在双向因果/潜在混杂因素。
图中用彩色箭头说明如下关系:
✅ 雨影响抗议:下雨越多,人越不愿意上街。
❌ 雨与政策变化无直接关系:政府不会因为天气不好就修改政策。
✅ 因此,雨——通过“影响抗议规模”——间接影响政策变化,但并不直接相关。
这正是工具变量的核心思想。
三、什么是工具变量(Instrumental Variable, IV)
定义:
工具变量是一个与自变量高度相关,但与因变量无关的外部变量,用于解决内生性问题,获得更可靠的因果估计。
在我们的例子中:
| 概念 | 实际变量 |
|---|---|
| 工具变量(IV) | 降雨量 |
| 自变量(X) | 抗议规模 |
| 因变量(Y) | 政策变化 |
| 内生性路径 | 抗议规模 ←→ 政策变化 |
四、使用工具变量的条件
要成为合格的工具变量,一个变量必须同时满足两个条件:
相关性条件(Relevance):工具变量与内生解释变量高度相关。
比如:雨量明显影响抗议规模。排除性假设(Exclusion Restriction):工具变量不能直接影响因变量,且不能通过其他路径间接影响因变量。
雨量不会直接或通过其他路径影响政策变化。
图中通过“雨”和“政策变化”之间用虚线标注“不相互关联的”来说明这一点。
五、直觉理解:为什么“雨”可以作为工具变量?
下雨并不会让政府改变政策,但却会让人们减少抗议。这种“只影响中介变量但不影响结果变量”的特性,就是工具变量的精髓。
我们可以理解为:
我们用“雨”去替代“抗议规模”来消除它和政策变化之间潜在的双向因果或共同原因。
如果我们能确定雨只是影响抗议,而不会影响政策,那么我们就可以更“干净地”估计抗议→政策的因果关系。
六、如何在实践中使用 IV?
在回归模型中,工具变量主要通过两阶段最小二乘法(2SLS)进行建模:
第一阶段回归:

→ 得到“预测的抗议规模”
第二阶段回归:

→ 由“只受工具变量影响的抗议规模”去估计政策变化,消除内生性。
七、应用场景举例
工具变量广泛应用于以下场景:
| 场景 | 工具变量示例 |
|---|---|
| 教育回报率 | 离学校的距离(影响受教育年限,但不直接影响收入) |
| 医疗影响 | 医生惯例(决定开药与否,但不直接影响病人健康) |
| 媒体影响 | 广播信号强度(影响收听率但不直接影响投票) |
八、总结
| 工具变量特点 | 举例解释 |
|---|---|
| 与解释变量强相关 | 雨影响抗议 |
| 与因变量无直接关系 | 雨与政策无关 |
| 解决因果混淆 | 清除双向因果与混杂变量 |
图中用简洁清晰的方式展示了一个合格工具变量的判断逻辑,让我们不再将其视作晦涩的计量术语,而是一个能够破解内生性困境的模型工具。
拓展阅读
Angrist & Krueger (1991). Does compulsory schooling affect earnings?
《Mostly Harmless Econometrics》:计量经济学名著
Python 实践推荐库:
linearmodels.iv模块
后记
你是否曾遇到“变量之间相互影响、不知道该怎么建模”的问题?你是否怀疑自己的回归结果“并不能真正解释因果”?试试工具变量方法,也许它能为你提供一个“曲线救国”的思路。
如果你觉得这篇图解文章对你有帮助,欢迎点赞、收藏、关注我,我们下篇再见!