MATLAB 是数学建模的强大工具,其丰富的函数库和可视化能力可以高效解决各类数学建模问题。以下是 MATLAB 数学建模的完整指南,涵盖建模流程、常用方法、代码示例及实际应用。
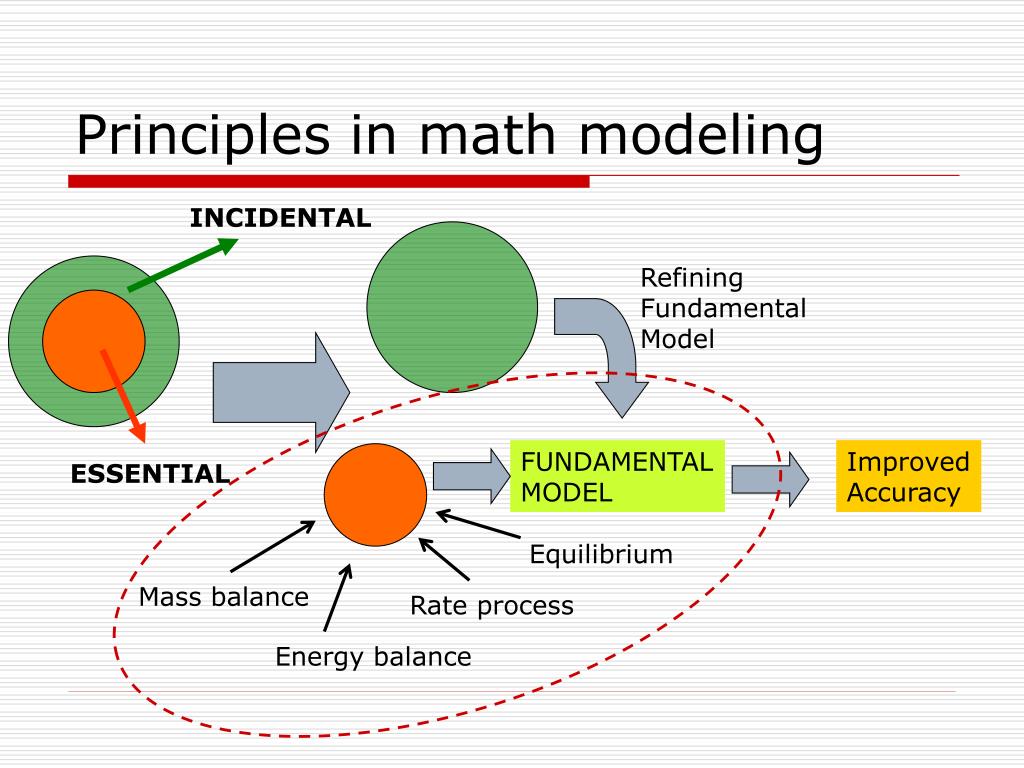
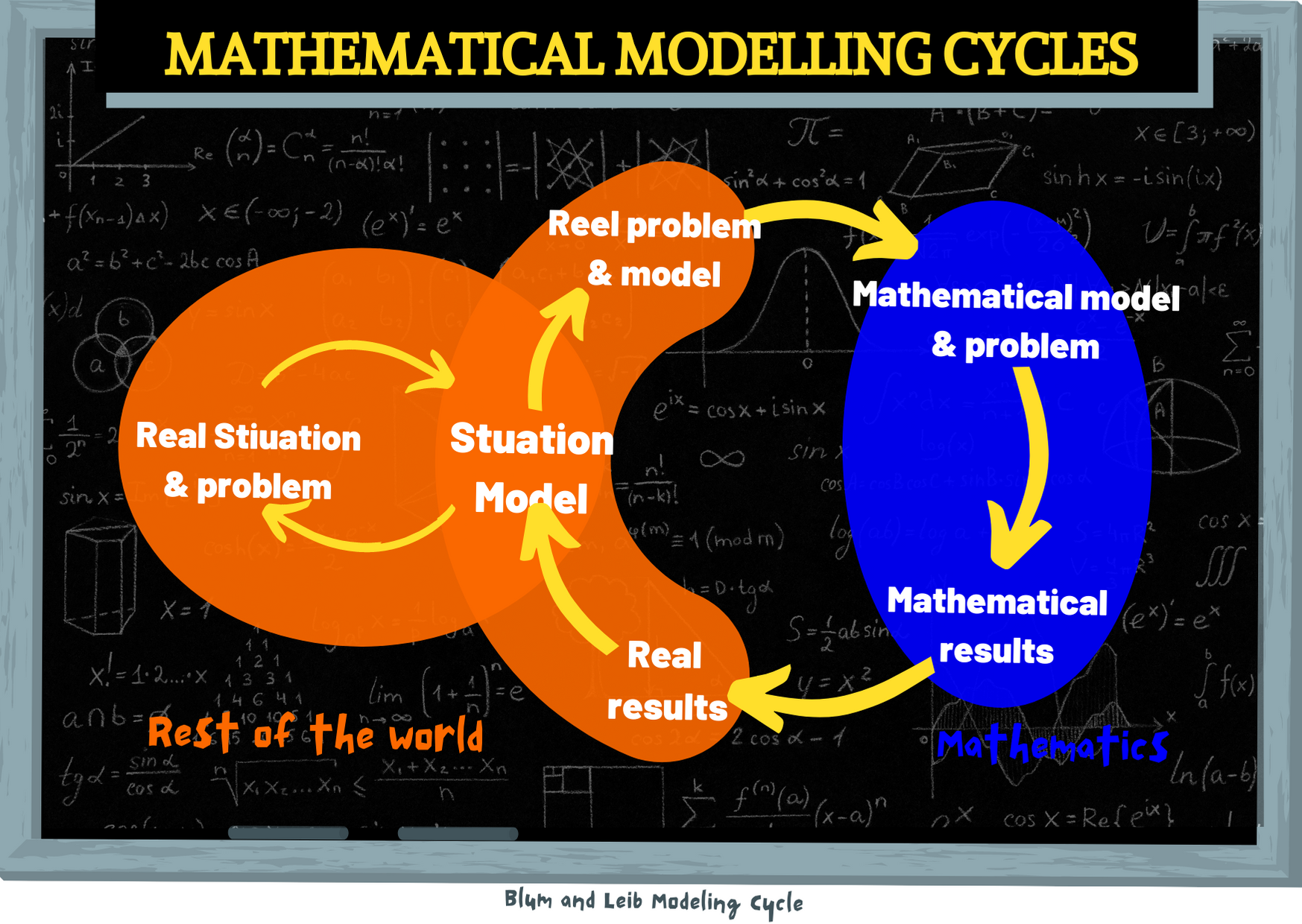
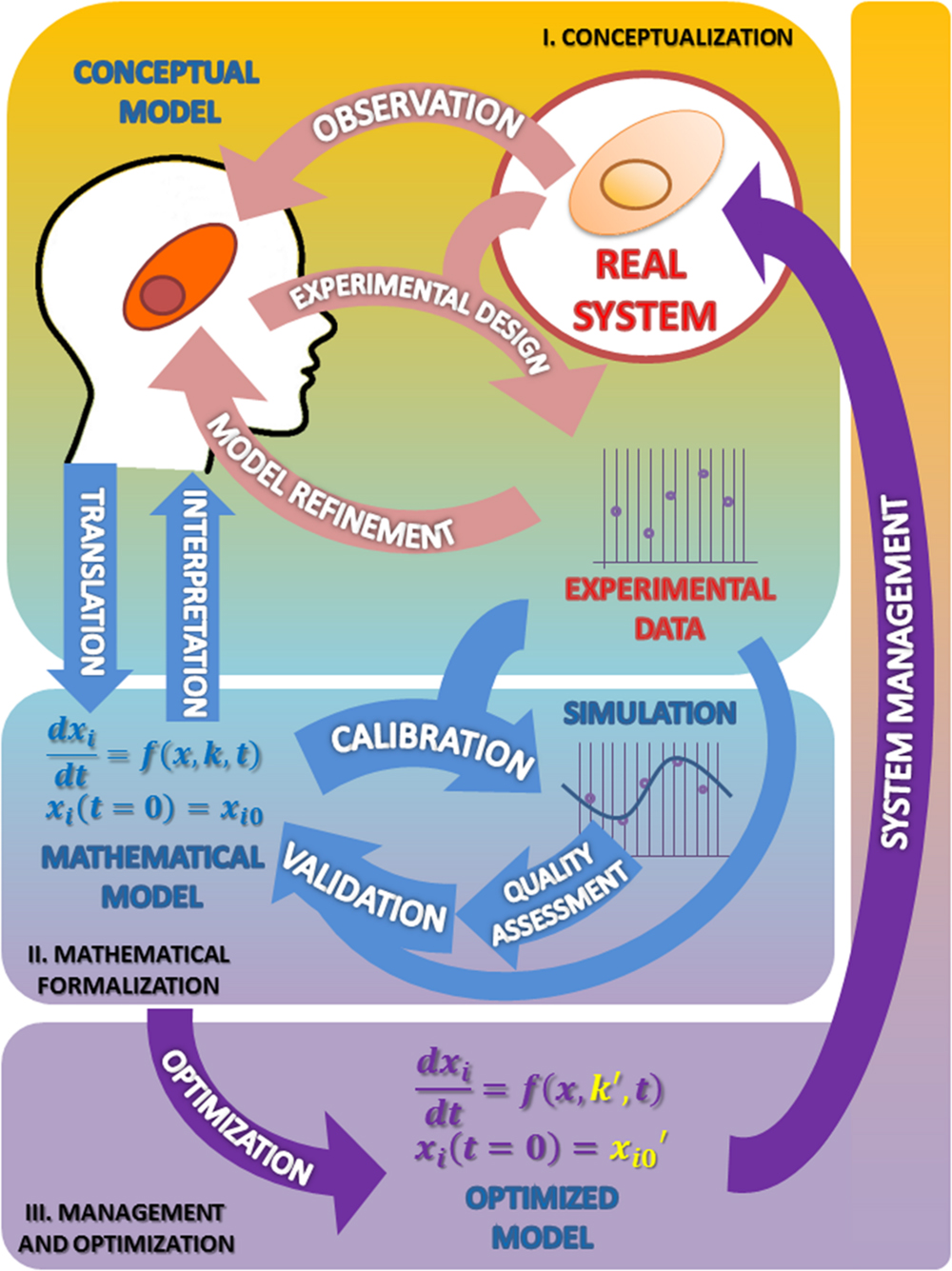
一、数学建模的基本流程
问题分析
• 明确目标(预测、优化、分类等)• 确定变量与约束条件
• 选择数学模型类型(连续/离散、确定性/随机性)。
模型构建
• 建立数学方程(微分方程、代数方程、统计模型等)。• 确定参数与初始条件。
模型求解
• 解析解(符号计算)• 数值解(数值方法、优化算法)。
模型验证
• 与实际数据对比(误差分析)。• 敏感性分析(参数影响)。
结果分析与应用
• 可视化输出。• 提出决策建议。
二、MATLAB 数学建模核心工具箱
| 工具箱 | 功能 | 典型应用场景 |
|---|---|---|
| Optimization Toolbox | 线性/非线性优化、全局优化 | 资源分配、参数调优 |
| Statistics and Machine Learning | 统计分析、机器学习 | 回归模型、分类问题 |
| PDE Toolbox | 偏微分方程求解 | 流体力学、热传导问题 |
| Symbolic Math Toolbox | 符号计算、公式推导 | 解析解、方程化简 |
| Global Optimization | 全局优化算法(遗传算法、模拟退火) | 复杂非线性优化问题 |

三、常见数学模型与 MATLAB 实现
1. 线性规划模型
问题:最小化成本 min c T x \min c^T x mincTx,满足 A x ≤ b Ax \leq b Ax≤b
% 定义目标函数和约束
c = [3; 5]; % 成本系数
A = [1 2; 4 1]; % 不等式约束矩阵
b = [8; 10]; % 约束右侧值
lb = [0; 0]; % 变量下界
% 求解线性规划
[x, fval] = linprog(c, A, b, [], [], lb, []);
disp(['最优解: x = ', num2str(x'), ', 最小成本: ', num2str(fval)]);
2. 微分方程模型(人口增长)
模型:Logistic 方程 d P d t = r P ( 1 − P K ) \frac{dP}{dt} = rP(1 - \frac{P}{K}) dtdP=rP(1−KP)
% 定义微分方程
function dPdt = logistic_model(t, P)
r = 0.1; K = 1000;
dPdt = r * P * (1 - P/K);
end
% 求解微分方程
[t, P] = ode45(@logistic_model, [0 50], 100);
% 绘图
plot(t, P); xlabel('时间'); ylabel('人口');
3. 优化模型(非线性最小二乘)
问题:拟合曲线 y = a e b x y = a e^{bx} y=aebx 到实验数据
% 生成模拟数据
x = 0:0.1:5;
y_true = 2*exp(-1.5*x);
y_noise = y_true + 0.5*randn(size(x));
% 定义目标函数
fun = @(params) params(1)*exp(params(2)*x) - y_noise;
% 初始猜测
params0 = [1, -1];
% 非线性最小二乘优化
params_opt = lsqnonlin(fun, params0);
% 拟合结果
a_opt = params_opt(1); b_opt = params_opt(2);
disp(['拟合参数: a = ', num2str(a_opt), ', b = ', num2str(b_opt)]);
4. 概率模型(蒙特卡洛模拟)
问题:估计积分 ∫ 0 1 x 2 d x \int_0^1 x^2 dx ∫01x2dx
N = 1e6; % 模拟次数
x = rand(N, 1); % 生成 [0,1] 均匀分布随机数
integral_estimate = mean(x.^2); % 蒙特卡洛积分
disp(['积分估计值: ', num2str(integral_estimate)]);
四、数据处理与可视化
1. 数据导入与清洗
% 读取 CSV 文件
data = readtable('experiment_data.csv');
% 处理缺失值
data(cleanmissing(data(:, :)), :);
% 数据标准化
data_normalized = zscore(data(:, 2:end));
2. 高级可视化
% 动态绘图(微分方程解)
h = animatedline;
for t = 1:length(t_values)
addpoints(h, t_values(t), P(t));
drawnow limitrate;
end
% 3D 曲面图(参数优化结果)
[X, Y] = meshgrid(0:0.1:5, 0:0.1:5);
Z = X.^2 + Y.^2;
surf(X, Y, Z); hold on;
plot3(a_opt, b_opt, params_opt(1)^2 + params_opt(2)^2, 'ro');
3. 交互式 App 设计
使用 App Designer 创建实时参数调整界面:
app = uifigure;
slider = uislider(app, 'Position', [20 20 200 5]);
plot_area = uiaxes(app);
xlabel(plot_area, '时间'); ylabel(plot_area, '人口');

五、实际建模技巧与注意事项
模型简化
• 忽略次要因素(如空气阻力在短距离运动中可忽略)。• 使用无量纲化减少变量数量。
参数敏感性分析
% 定义参数范围 params_range = [0.1, 0.2, 0.3; 1, 2, 3]; % 生成拉丁超立方采样 inputs = lhsdesign(100, 2); % 计算输出并分析敏感度 outputs = arrayfun(@(i) model(inputs(i,:)), 1:100);验证与误差分析
• 使用交叉验证(cvpartition函数)。• 计算均方误差(MSE)或平均绝对误差(MAE)。
高性能计算
• 使用parfor进行并行计算。• 利用 GPU 加速(
gpuArray)。
六、经典案例参考
SIR 传染病模型
% 定义 SIR 方程 function dydt = sir_model(t, y) beta = 0.3; gamma = 0.1; S = y(1); I = y(2); R = y(3); dydt = [-beta*S*I, beta*S*I - gamma*I, gamma*I]; end % 求解并绘图 [t, y] = ode45(@sir_model, [0 100], [0.99, 0.01, 0]); plot(t, y(:,1), 'b', t, y(:,2), 'r');交通流模型(Lighthill-Whitham-Richards PDE)
% 使用 PDE Toolbox 求解一维交通流方程 model = createpde(1); geometryFromEdges(model, @(p) [p(1,1); p(1,2)]); specifyCoefficients(model, 'm', 0, 'd', 1, 'c', -u^2, 'a', 0, 'f', 0);
七、学习资源推荐
MATLAB 官方文档
• 数学建模工具箱书籍
• 《MATLAB 数学建模与仿真》—— 薛定宇• 《Introduction to Applied Linear Algebra》—— Boyd & Vandenberghe
在线课程
• Coursera: Modeling and Simulation in MATLAB
通过掌握以上方法,你可以用 MATLAB 快速构建、求解和验证数学模型,解决工程、经济、生物等领域的实际问题。核心在于:明确问题 → 选择模型 → 工具实现 → 结果分析。