一图理解线性插值(Linear Interpolation):填补缺失数据的优雅方案
一、前言
在数据科学与机器学习的世界中,缺失数据是常态而非例外。面对这些空缺值,我们有很多种处理策略:删除、填充、预测等。而在所有填充方法中,线性插值(Linear Interpolation)是一种简单、直观且有效的技术。
今天,我们就通过下面这张手绘图,一起直观地理解线性插值的原理和实现方式。
二、什么是线性插值?
图中清晰地写道:
“在线性插值中,我们在已知的数值之间画一条线,来填补缺失数值的一种策略。”
换句话说:
给定一些已知的数据点,我们在这些点之间画直线。
然后我们根据直线的斜率,来推测中间未知点的数值。
这就好像你知道早上 9 点和中午 12 点的温度,想要估算 10 点和 11 点的温度——线性插值就可以帮你做到!
三、图示分析:一步一步看懂线性插值
我们来看图中内容:
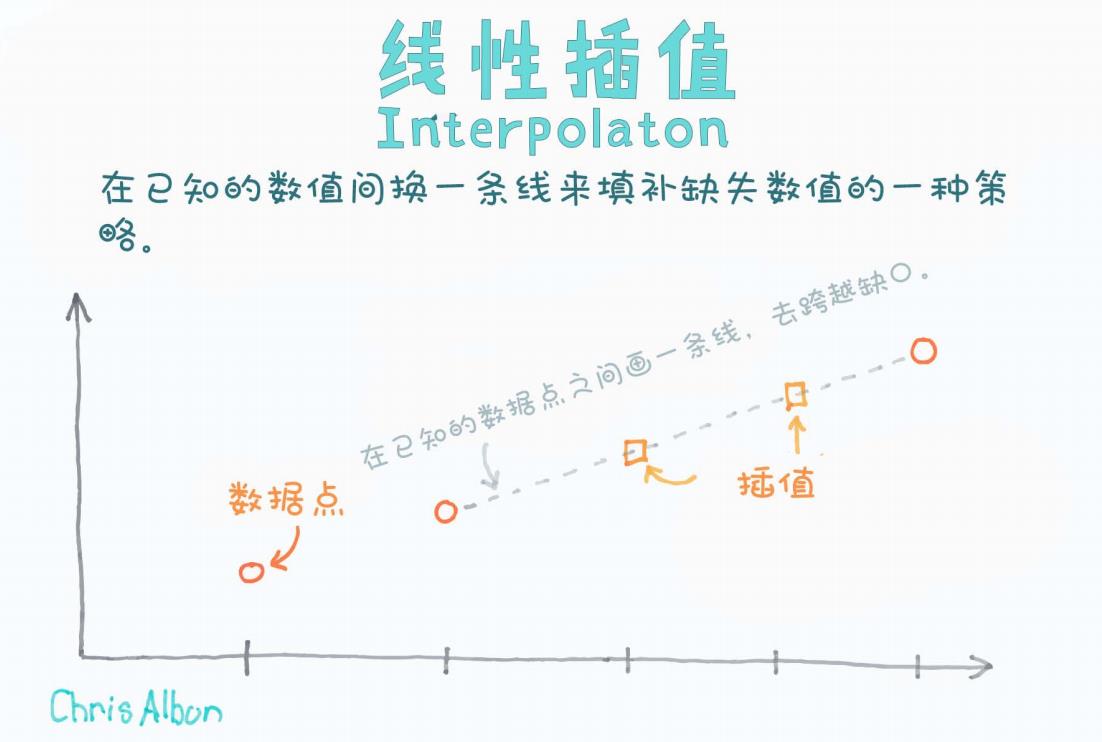
图中要素解释:
圆圈(○) 代表原始数据点(数据点)。这些是你已知的数值。
虚线代表在已知数据点之间作出的连接线。
方块(□)表示插值结果,也就是我们预测/估算出来的缺失数据。
箭头和注释形象说明了从数据点到插值点的过程。
图中还用简洁的语言说明了插值过程:“在已知的数据点之间画一条线,去跨越缺口。”
四、数学原理:用公式来表达线性插值
设你已知两个点:
点 A:
点 B:
你要估算一个处于 和
之间、横坐标为 x 的点的纵坐标 y。
插值公式如下:
这个公式的核心思想就是:按比例线性过渡。
简单来说,这和我们小时候画斜率公式“直线过两点”的过程一样。
五、代码实现(Python 示例)
在实际项目中,线性插值通常通过 Pandas 或 NumPy 实现,以下是一个简单示例:
import pandas as pd
import numpy as np
# 模拟一个缺失值的数据序列
data = pd.Series([1.0, np.nan, np.nan, 4.0])
# 进行线性插值
interpolated = data.interpolate(method='linear')
print(interpolated)
输出结果:
0 1.0
1 2.0
2 3.0
3 4.0
dtype: float64
是不是非常直观?这就是图中方块插值点的实际计算过程。
六、应用场景
线性插值虽然简单,但用途非常广泛:
数据清洗:用于填补时间序列中的缺失值;
图像处理:在缩放图像时进行像素值估算;
动画插帧:计算关键帧之间的过渡;
金融建模:填补历史价格数据;
传感器数据补全:如 IoT 设备中断数据修复。
七、线性插值的优缺点
| 优点 | 缺点 |
|---|---|
| 简单快速,容易实现 | 不能处理非线性变化趋势 |
| 没有引入外部假设 | 插值点可能不够平滑 |
| 很适合实时或在线数据填补 | 对突变数据敏感 |
八、结语
线性插值虽然只是数据插值的“入门款”,但它的直观性和高效性,让它在无数真实项目中都大放异彩。
通过这张生动的手绘图,我们不仅了解了线性插值的定义,还掌握了其数学原理与代码实现方式。希望你在日常的数据处理过程中,能灵活地应用这一小而美的技巧。
如果你喜欢这类“图解算法”内容,欢迎点赞、收藏和关注,后续我将持续更新更多直观易懂的图解知识!
参考资料:
Chris Albon 手绘图:数据科学视觉笔记
Pandas 官方文档:pandas - Python Data Analysis Library
《Python 数据科学手册》