历年数一真题及答案下载直通车
已知函数 f ( x ) = ∫ 0 x e cos t d t f(x) = \int_0^x e^{\cos t} dt f(x)=∫0xecostdt, g ( x ) = ∫ 0 sin x e t 2 d t g(x) = \int_0^{\sin x} e^{t^2} dt g(x)=∫0sinxet2dt,则( )。
A. f ( x ) f(x) f(x) 为奇函数, g ( x ) g(x) g(x) 为偶函数
B. f ( x ) f(x) f(x) 为偶函数, g ( x ) g(x) g(x) 为奇函数
C. f ( x ) f(x) f(x) 与 g ( x ) g(x) g(x) 均为奇函数
D. f ( x ) f(x) f(x) 与 g ( x ) g(x) g(x) 均为周期函数设 P = P ( x , y , z ) P = P(x, y, z) P=P(x,y,z), Q = Q ( x , y , z ) Q = Q(x, y, z) Q=Q(x,y,z) 均为连续函数, ∑ \sum ∑ 为曲面 z = 1 − x 2 − y 2 z = \sqrt{1 - x^2 - y^2} z=1−x2−y2 ( x ≥ 0 x \geq 0 x≥0, y ≥ 0 y \geq 0 y≥0) 的上侧,则 ∬ Σ P d y d z + Q d z d x = ()。 \iint_{\Sigma} P dy dz + Q dz dx =( )。 ∬ΣPdydz+Qdzdx=()。
A. ∬ Σ ( x z P + y z Q ) d x d y \iint_{\Sigma} \left( \frac{x}{z} P + \frac{y}{z} Q \right) dxdy ∬Σ(zxP+zyQ)dxdy
B. ∬ Σ ( − x z P + y z Q ) d x d y \iint_{\Sigma} \left( -\frac{x}{z} P + \frac{y}{z} Q \right) dxdy ∬Σ(−zxP+zyQ)dxdy
C. ∬ Σ ( x z P − y z Q ) d x d y \iint_{\Sigma} \left( \frac{x}{z} P - \frac{y}{z} Q \right) dxdy ∬Σ(zxP−zyQ)dxdy
D. ∬ Σ ( − x z P − y z Q ) d x d y \iint_{\Sigma} \left( -\frac{x}{z} P - \frac{y}{z} Q \right) dxdy ∬Σ(−zxP−zyQ)dxdy已知幂函数 ∑ n = 0 ∞ a n x n \sum_{n=0}^{\infty} a_n x^n ∑n=0∞anxn 的和函数为 ln ( 2 + x ) \ln(2+x) ln(2+x),则 ∑ n = 0 ∞ n a 2 n = \sum_{n=0}^{\infty} n a_{2n} = ∑n=0∞na2n=( )。
A. − 1 6 -\frac{1}{6} −61
B. − 1 3 -\frac{1}{3} −31
C. 1 6 \frac{1}{6} 61
D. 1 3 \frac{1}{3} 31设函数 f ( x ) f(x) f(x) 在区间 ( − 1 , 1 ) (-1,1) (−1,1) 内有定义, lim x → 0 f ( x ) = 0 \lim_{x \to 0} f(x) = 0 limx→0f(x)=0,则( )。
A. 当 lim x → 0 f ( x ) x = m \lim_{x \to 0} \frac{f(x)}{x} = m limx→0xf(x)=m 时, f ′ ( 0 ) = m f'(0) = m f′(0)=m
B. 当 f ′ ( 0 ) = m f'(0) = m f′(0)=m 时, lim x → 0 f ( x ) x = m \lim_{x \to 0} \frac{f(x)}{x} = m limx→0xf(x)=m
C. 当 lim x → 0 f ′ ( x ) = m \lim_{x \to 0} f'(x) = m limx→0f′(x)=m 时, f ′ ( 0 ) = m f'(0) = m f′(0)=m
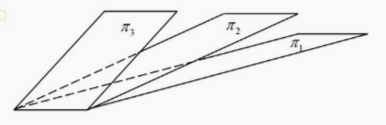
D. 当 f ′ ( 0 ) = m f'(0) = m f′(0)=m 时, lim x → 0 f ′ ( x ) = m \lim_{x \to 0} f'(x) = m limx→0f′(x)=m在空间直角坐标系 O − x y z O - xyz O−xyz 中,三张平面 π i : a i x + b i y + c i z = d i \pi_i: a_ix + b_iy + c_iz = d_i πi:aix+biy+ciz=di ( i = 1 , 2 , 3 i = 1,2,3 i=1,2,3) 位置关系如图所示,记 α i = ( a i , b i , c i ) \alpha_i = (a_i, b_i, c_i) αi=(ai,bi,ci), β i = ( a i , b i , c i , d i ) \beta_i = (a_i, b_i, c_i, d_i) βi=(ai,bi,ci,di),若 r ( α 1 α 2 α 3 ) = m r\begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{pmatrix} = m r α1α2α3 =m, r ( β 1 β 2 β 3 ) = n r\begin{pmatrix} \beta_1 \\ \beta_2 \\ \beta_3 \end{pmatrix} = n r β1β2β3 =n,则( )。
A. n = 1 n=1 n=1, n = 2 n=2 n=2
B. m = n = 2 m=n=2 m=n=2
C. m = 2 m=2 m=2, n = 3 n=3 n=3
D. m = n = 3 m=n=3 m=n=3
设向量 α 1 = ( a 1 − 1 1 ) \alpha_1 = \begin{pmatrix} a \\ 1 \\ -1 \\ 1 \end{pmatrix} α1= a1−11 , α 2 = ( 1 1 b a ) \alpha_2 = \begin{pmatrix} 1 \\ 1 \\ b \\ a \end{pmatrix} α2= 11ba , α 3 = ( 1 a − 1 1 ) \alpha_3 = \begin{pmatrix} 1 \\ a \\ -1 \\ 1 \end{pmatrix} α3= 1a−11 ,若 α 1 , α 2 , α 3 \alpha_1, \alpha_2, \alpha_3 α1,α2,α3 线性相关,且其中任意两个向量均线性无关,则( )。
A. a = 1 a=1 a=1, b ≠ − 1 b \neq -1 b=−1
B. a = 1 a=1 a=1, b = − 1 b=-1 b=−1
C. a ≠ − 2 a \neq -2 a=−2, b = 2 b=2 b=2
D. a = − 2 a=-2 a=−2, b = 2 b=2 b=23阶矩阵 A A A 的秩为2,非零向量 α \alpha α 满足 A α = 0 A\alpha = 0 Aα=0,任意向量 β \beta β,使得 β T α = 0 \beta^T\alpha = 0 βTα=0,且 A β = β A\beta = \beta Aβ=β,则下列结论正确的是( )。
A. A 3 A^3 A3 的迹为2
B. A 3 A^3 A3 的迹为5
C. A 5 A^5 A5 的迹为7
D. A 5 A^5 A5 的迹为9设随机变量 X X X 与 Y Y Y 独立, X X X 服从 N ( 0 , 2 ) N(0, 2) N(0,2) 的正态分布, Y Y Y 服从 N ( − 2 , 2 ) N(-2, 2) N(−2,2) 的正态分布,若 P { 2 X + Y < a = P { X > Y } P\{2X+Y < a = P\{X > Y\} P{2X+Y<a=P{X>Y},则 a = a= a=( )。
A. − 2 − 10 -2 - \sqrt{10} −2−10
B. − 2 + 10 -2+\sqrt{10} −2+10
C. − 2 − 6 -2 - \sqrt{6} −2−6
D. − 2 + 6 -2+\sqrt{6} −2+6设随机变量 X X X 的概率密度为 f ( x ) = { 2 ( 1 − x ) , 0 < x < 1 0 , 其它 f(x) = \begin{cases} 2(1-x), & 0 < x < 1 \\ 0, & \text{其它} \end{cases} f(x)={2(1−x),0,0<x<1其它,在 X = x X = x X=x ( 0 < x < 1 0 < x < 1 0<x<1)的条件下, Y Y Y 在区间 ( x , 1 ) (x, 1) (x,1) 上服从均匀分布,则 Cov ( X , Y ) = \text{Cov}(X, Y) = Cov(X,Y)=( )。
A. − 1 36 -\frac{1}{36} −361
B. − 1 72 -\frac{1}{72} −721
C. 1 72 \frac{1}{72} 721
D. 1 36 \frac{1}{36} 361设随机变量 X X X、 Y Y Y 相互独立,且均服从参数为 λ \lambda λ 的指数分布,令 Z = ∣ X − Y ∣ Z=|X-Y| Z=∣X−Y∣,则下列随机变量与 Z Z Z 同分布的是( )。
A. X + Y X+Y X+Y
B. X + Y 2 \frac{X+Y}{2} 2X+Y
C. 2 X 2X 2X
D. X X X若 lim x → 0 ( 1 + a x 2 ) sin x − 1 x 3 = 6 \lim_{x \to 0} \frac{(1 + a x^2)^{\sin x} - 1}{x^3} = 6 limx→0x3(1+ax2)sinx−1=6,则 a = ‾ a = \underline{\quad\quad} a=
z = f ( u , v ) z = f(u, v) z=f(u,v) 有二阶连续导数, d f ∣ ( 1 , 1 ) = 3 d u + 4 d v df|_{(1,1)} = 3du + 4dv df∣(1,1)=3du+4dv, y = f ( cos x , 1 + x 2 ) y = f(\cos x, 1 + x^2) y=f(cosx,1+x2),则 d 2 y d x 2 ∣ x = 0 = ‾ \frac{d^2y}{dx^2} \bigg|_{x=0} = \underline{\quad\quad} dx2d2y x=0=
若函数 f ( x ) = x + 1 f(x) = x + 1 f(x)=x+1, f ( x ) = a 0 2 + ∑ n = 0 ∞ a n cos n x f(x) = \frac{a_0}{2} + \sum_{n=0}^{\infty} a_n \cos nx f(x)=2a0+∑n=0∞ancosnx, x ∈ [ 0 , π ] x \in [0, \pi] x∈[0,π],则极限 lim n → ∞ n x sin a 2 n − 1 = ‾ \lim_{n \to \infty} n^x \sin a_{2n-1} = \underline{\quad\quad} limn→∞nxsina2n−1=
微分方程 y ′ = 1 ( x + y ) 2 y' = \frac{1}{(x+y)^2} y′=(x+y)21,满足条件 y ( 1 ) = 0 y(1) = 0 y(1)=0 的解为 ‾ \underline{\quad\quad}
设实矩阵 A = ( a + 1 a a a ) A = \begin{pmatrix} a+1 & a \\ a & a \end{pmatrix} A=(a+1aaa),若对任意实向量 α = ( x 1 x 2 ) \alpha = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} α=(x1x2), β = ( y 1 y 2 ) \beta = \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} β=(y1y2), ( α T A β ) 2 ≤ α T A α ⋅ β T A β (\alpha^T A \beta)^2 \leq \alpha^T A \alpha · \beta^T A \beta (αTAβ)2≤αTAα⋅βTAβ 都成立,则 a a a 的取值范围是 ‾ \underline{\quad\quad}
随机试验每次成功的概率为 P P P,现进行三次独立重复实验,已知至少成功一次的条件下全部成功概率为 4 13 \frac{4}{13} 134,则 P = ‾ P = \underline{\quad\quad} P=
已知平面区域 D = { ( x , y ) ∣ 1 − y 2 ≤ x ≤ 1 , − 1 ≤ y ≤ 1 } D = \{(x, y) | \sqrt{1 - y^2} \leq x \leq 1, -1 \leq y \leq 1\} D={(x,y)∣1−y2≤x≤1,−1≤y≤1},计算 ∬ D x x 2 + y 2 d σ \iint_D \frac{x}{\sqrt{x^2 + y^2}} \, d\sigma ∬Dx2+y2xdσ
设 f ( x , y ) = x 3 + y 3 − ( x + y ) 2 + 3 f(x, y) = x^3 + y^3 - (x+y)^2 + 3 f(x,y)=x3+y3−(x+y)2+3,曲面 z = f ( x , y ) z = f(x, y) z=f(x,y) 在 ( 1 , 1 , 1 ) (1, 1, 1) (1,1,1) 处的切平面为 T T T, T T T 与三个坐标面所围有界区域在 x o y xoy xoy 面的投影为 D D D
(1) 求 T T T 的方程
(2) 求 f ( x , y ) f(x, y) f(x,y) 在 D D D 上的最大值和最小值设 f ( x ) f(x) f(x) 二阶可导, f ′ ( 0 ) = f ′ ( 1 ) f'(0) = f'(1) f′(0)=f′(1), ∣ f ′ ′ ( x ) ∣ ≤ 1 |f''(x)| \leq 1 ∣f′′(x)∣≤1,证明:
1) 当 x ∈ ( 0 , 1 ) x \in (0, 1) x∈(0,1) 时 ∣ f ( x ) − f ( 0 ) ( 1 − x ) − f ( 1 ) x ∣ ≤ x ( 1 − x ) 2 |f(x) - f(0)(1-x) - f(1)x| \leq \frac{x(1-x)}{2} ∣f(x)−f(0)(1−x)−f(1)x∣≤2x(1−x)
2) ∣ ∫ 0 1 f ( x ) d x − f ( 0 ) + f ( 1 ) 2 ∣ ≤ 1 12 \left| \int_0^1 f(x) dx - \frac{f(0) + f(1)}{2} \right| \leq \frac{1}{12} ∫01f(x)dx−2f(0)+f(1) ≤121已知有向曲线 L L L 为球面 x 2 + y 2 + z 2 = 2 x x^2 + y^2 + z^2 = 2x x2+y2+z2=2x 与平面 2 x − z − 1 = 0 2x - z - 1 = 0 2x−z−1=0 的交线从 z z z 轴正向往 z z z 轴负向看去为逆时针方向,计算曲线积分 ∫ L ( 6 x y z − y z 2 ) d x + 2 x 2 z d y + x y z d z \int_L (6xyz - yz^2) dx + 2x^2z dy + xyz dz ∫L(6xyz−yz2)dx+2x2zdy+xyzdz
已知数列 { x n } \{x_n\} {xn}, { y n } \{y_n\} {yn}, { z n } \{z_n\} {zn} 满足 x 0 = − 1 x_0 = -1 x0=−1, y 0 = 0 y_0 = 0 y0=0, z 0 = 2 z_0 = 2 z0=2,且
{ x n = − 2 x n − 1 + 2 z n − 1 y n = − 2 y n − 1 − 2 z n − 1 z n = − 6 x n − 1 − 3 y n − 1 + 3 z n − 1 \begin{cases} x_n = -2x_{n-1} + 2z_{n-1} \\ y_n = -2y_{n-1} - 2z_{n-1} \\ z_n = -6x_{n-1} - 3y_{n-1} + 3z_{n-1} \end{cases} ⎩ ⎨ ⎧xn=−2xn−1+2zn−1yn=−2yn−1−2zn−1zn=−6xn−1−3yn−1+3zn−1
记 α n = ( x n y n z n ) \alpha_n = \begin{pmatrix} x_n \\ y_n \\ z_n \end{pmatrix} αn= xnynzn ,写出满足 α n = A α n − 1 \alpha_n = A \alpha_{n-1} αn=Aαn−1 的矩阵 A A A,并求 A n A^n An 及 x n x_n xn, y n y_n yn, z n z_n zn ( n = 1 , 2 , ⋯ n = 1, 2, \cdots n=1,2,⋯)
- 设总体 X ∼ U [ 0 , θ ] X \sim U[0, \theta] X∼U[0,θ] 上的均匀分布,其中 $ \theta \in (0, + \infty) 为未知参数, 为未知参数, 为未知参数,X_1, X_2, \cdots, X_n$ 为来自总体 X X X 简单随机样本, X ( n ) = max { X 1 , X 2 , ⋯ , X n } X(n) = \max\{X_1, X_2, \cdots, X_n\} X(n)=max{X1,X2,⋯,Xn}, T c = c X ( n ) T_c = cX(n) Tc=cX(n)
(1) 求 c c c 时,使得 T c T_c Tc 为 θ \theta θ 的无偏估计
(2) 记 h ( c ) = E ( T c − θ ) 2 h(c) = E(T_c - \theta)^2 h(c)=E(Tc−θ)2,求 c c c 使得 h ( c ) h(c) h(c) 最小