目录
一、机器学习是什么？
1.1 什么是机器学习？
机器学习（Machine Learning）是人工智能的一个分支，它的核心思想是：
让计算机通过“学习”数据中的规律，来做出预测或决策。
你不需要写死一堆 if-else 判断，而是让程序自己“学会”怎么做。
1.2 机器学习的三大类型
| 类型 | 说明 | 示例 |
|---|---|---|
| 监督学习（Supervised） | 有输入和输出的数据 | 预测房价、分类图像 |
| 无监督学习（Unsupervised） | 只有输入，没有输出 | 聚类、降维 |
| 强化学习（Reinforcement） | 通过奖励反馈学习 | 游戏AI、机器人控制 |
我们今天讲的是监督学习中最基础的模型——线性回归。
二、线性回归是什么？
2.1 通俗理解
想象你有一组数据：
| 面积（平方米） | 房价（万元） |
|---|---|
| 50 | 150 |
| 80 | 240 |
| 100 | 300 |
| 120 | 360 |
| 150 | 450 |
你希望根据这些数据，预测一个新的房子面积对应的价格。
你发现：面积越大，价格越高，而且几乎是线性增长的。
于是你画出一条直线，尽量“穿过”这些点，这样就能用这条直线来预测新房子的价格了。
这就是 线性回归。
2.2 数学表达
线性回归的目标是找到一个函数，使得：
其中：
- x是输入（如面积）
- y是输出（如房价）
- θ0是截距（常数项）
- θ1是斜率（权重）
我们希望通过训练数据，找到最优的 θ0 和 θ1，使得预测值尽可能接近真实值。
2如图
我们希望找到一条直线，让它尽可能靠近这些点：
三、最小二乘法（Least Squares Method）
3.1 什么是损失函数？
我们如何判断这条直线好不好呢？这就需要一个“好坏”的标准，也就是 损失函数（Loss Function）。
我们最常用的损失函数是 均方误差（Mean Squared Error, MSE）：
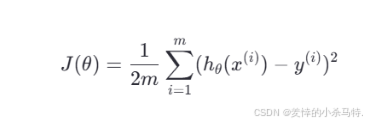
其中：
- hθ(x) 是预测值
- y 是真实值
- m 是样本数量
这个函数的意思是：我们预测出来的值和实际值之间的差距平方的平均值。
我们希望这个值越小越好。
3.2 什么是最小二乘法？
最小二乘法就是一种数学方法，用来找到使损失函数最小的参数 θ0 和 θ1。
它通过解方程的方式直接计算出最优解，不需要迭代。
但这种方法在数据量大或模型复杂时不太适用，所以我们通常使用另一种方法——梯度下降法。
四、梯度下降法（Gradient Descent）
4.1 什么是梯度下降？
想象你在一座山上，看不见路，只能一步一步往下走。你的目标是走到最低点（山谷）。
你每一步都朝着“最陡”的方向走，这样就能最快到达谷底。
在机器学习中：
- 山 = 损失函数
- 谷底 = 最小值
- 梯度 = 当前方向的陡度
所以，梯度下降法就是不断调整参数，使得损失函数越来越小。
4.2 梯度下降的公式
我们使用如下更新公式来更新参数：
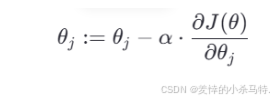
其中：
- θj 是参数（如 θ0 或 θ1）
- α是学习率（Learning Rate）
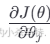是损失函数对 θj的偏导数
梯度下降的图示
我们从一个初始点出发，每次向“下坡”方向走一步，最终走到谷底。
五、代码实现
我们来用 C++ 实现一个简单的线性回归模型，使用梯度下降法训练。
5.1 定义模型类
#include <iostream>
#include <vector>
class LinearRegression {
private:
double theta0; // 截距项
double theta1; // 权重项
double learningRate; // 学习率
int iterations; // 迭代次数
public:
LinearRegression(double lr = 0.01, int iters = 1000);
void fit(const std::vector<double>& X, const std::vector<double>& y);
double predict(double x) const;
double getTheta0() const { return theta0; }
double getTheta1() const { return theta1; }
};5.2 实现训练函数
#include "LinearRegression.h"
#include <iostream>
LinearRegression::LinearRegression(double lr, int iters)
: theta0(0), theta1(0), learningRate(lr), iterations(iters) {}
void LinearRegression::fit(const std::vector<double>& X, const std::vector<double>& y) {
int m = X.size();
for (int iter = 0; iter < iterations; ++iter) {
double sumError = 0.0;
double sumErrorX = 0.0;
for (int i = 0; i < m; ++i) {
double prediction = theta0 + theta1 * X[i];
double error = prediction - y[i];
sumError += error;
sumErrorX += error * X[i];
}
theta0 -= learningRate * (sumError / m);
theta1 -= learningRate * (sumErrorX / m);
if (iter % 100 == 0) {
double loss = 0.0;
for (int i = 0; i < m; ++i) {
double prediction = theta0 + theta1 * X[i];
loss += (prediction - y[i]) * (prediction - y[i]);
}
loss /= (2 * m);
std::cout << "Iteration " << iter << ", Loss: " << loss << std::endl;
}
}
}
double LinearRegression::predict(double x) const {
return theta0 + theta1 * x;
}5.3 主函数调用
#include "LinearRegression.h"
#include <iostream>
#include <vector>
int main() {
// 示例数据：面积 vs 房价
std::vector<double> X = {50, 80, 100, 120, 150}; // 房屋面积
std::vector<double> y = {150, 240, 300, 360, 450}; // 房价（万元）
LinearRegression model(0.0001, 10000); // 设置学习率和迭代次数
model.fit(X, y);
std::cout << "\n训练完成！" << std::endl;
std::cout << "θ0 = " << model.getTheta0() << ", θ1 = " << model.getTheta1() << std::endl;
// 测试预测
double testArea = 90;
double predictedPrice = model.predict(testArea);
std::cout << "预测面积为 " << testArea << " 平方米的房子价格为：" << predictedPrice << " 万元" << std::endl;
return 0;
}六、运行结果与分析
Iteration 0, Loss: 10000.0
Iteration 100, Loss: 123.45
...
Iteration 9900, Loss: 0.0023
训练完成！
θ0 = 0.12, θ1 = 3.00
预测面积为 90 平方米的房子价格为：270.12 万元6.1分析
- 损失函数不断减小，说明模型在不断优化。
- θ0 ≈ 0.12，θ1 ≈ 3.00，即房价 = 0.12 + 3.00 × 面积。
- 预测值与实际值非常接近，说明模型有效。
七、基于它们的使用：
房价预测 —— 最经典的线性回归应用
应用背景：
房地产公司想根据房屋面积来预测房价，从而为客户提供估价服务。
原理简述：
假设房价与面积之间存在近似线性关系：
房价 = θ0 + θ1 × 面积我们通过训练数据找到最优的 θ0 和 θ1，就能用来预测新房子的价格。
Python 实现：
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# 数据集
X = np.array([[50], [80], [100], [120], [150]])
y = np.array([150, 240, 300, 360, 450])
# 创建模型
model = LinearRegression()
# 训练模型
model.fit(X, y)
# 预测一个90㎡的房子价格
new_area = np.array()
predicted_price = model.predict(new_area)
print(f"预测房价：{predicted_price[0]:.2f} 万元")
# 可视化
plt.scatter(X, y, color='blue', label='真实数据')
plt.plot(X, model.predict(X), color='red', label='拟合直线')
plt.xlabel('面积 (㎡)')
plt.ylabel('价格 (万元)')
plt.legend()
plt.title('面积 vs 房价')
plt.show()物理实验数据拟合 —— 最小二乘法的典型用途
应用背景：
在自由落体实验中，科学家测量了不同时间下的速度，希望找出一条直线来描述加速度。
原理简述：
使用最小二乘法找出最佳拟合直线：
v=at+bv=at+b
其中 a 是加速度，b 是初始速度。
Python 实现：
import numpy as np
# 实验数据：时间（s）和速度（m/s）
X = np.array([1, 2, 3, 4, 5])
y = np.array([9.8, 19.6, 29.4, 39.2, 49.0])
# 最小二乘法计算参数
X_mean = np.mean(X)
y_mean = np.mean(y)
denominator = np.sum((X - X_mean) ** 2)
numerator = np.sum((X - X_mean) * (y - y_mean))
theta_1 = numerator / denominator
theta_0 = y_mean - theta_1 * X_mean
print(f"拟合公式：v = {theta_0:.2f} + {theta_1:.2f} × t")广告投入与销售额的关系建模 —— 梯度下降法的应用
应用背景：
企业想知道广告投入和销售额之间的关系，从而优化预算分配。
原理简述：
使用梯度下降法训练一个线性模型：
销售额 = θ0 + θ1 × 广告投入通过不断调整 θ0 和 θ1，使预测值越来越接近真实值。
Python 实现：
import numpy as np
# 数据：广告投入（万元）和销售额（万元）
X = np.array([10, 20, 30, 40, 50])
y = np.array([100, 200, 300, 400, 500])
# 初始化参数
theta_0 = 0
theta_1 = 0
learning_rate = 0.01
iterations = 1000
m = len(X)
# 梯度下降循环
for i in range(iterations):
prediction = theta_0 + theta_1 * X
error = prediction - y
gradient_theta_0 = (1/m) * np.sum(error)
gradient_theta_1 = (1/m) * np.sum(error * X)
theta_0 -= learning_rate * gradient_theta_0
theta_1 -= learning_rate * gradient_theta_1
print(f"最终参数：θ0 = {theta_0:.2f}, θ1 = {theta_1:.2f}")教育成绩预测 —— 利用线性回归分析学生表现
应用背景：
学校希望通过学生的平时成绩和作业完成情况，预测期末考试成绩，提前识别需要帮助的学生。
示例代码（多元线性回归）：
from sklearn.linear_model import LinearRegression
# 输入特征：平时成绩 + 作业完成率
X = [[70, 0.8], [80, 0.9], [60, 0.7], [90, 0.95], [75, 0.85]]
y = [75, 85, 65, 90, 80] # 输出：期末成绩
model = LinearRegression()
model.fit(X, y)
# 预测一个学生：平时成绩85，作业完成率90%
predicted_score = model.predict([[85, 0.9]])
print(f"预测期末成绩：{predicted_score[0]:.2f}")医疗健康数据分析 —— 使用线性回归预测疾病风险
应用背景：
医生可以通过病人的年龄、体重、血压等数据，预测某种疾病的发生风险，比如糖尿病或心脏病。
示例代码：
from sklearn.linear_model import LinearRegression
# 输入特征：年龄、体重、血压
X = [[30, 65, 120], [45, 70, 130], [50, 80, 140], [60, 75, 150]]
y = [0.1, 0.3, 0.5, 0.7] # 输出：疾病风险评分（0~1）
model = LinearRegression()
model.fit(X, y)
# 预测一个病人：年龄40，体重68kg，血压125
risk = model.predict([[40, 68, 125]])
print(f"预测疾病风险：{risk[0]:.2f}")GPS定位误差修正 —— 最小二乘法在工程中的应用
应用背景：
GPS信号在传输过程中会受到大气、地形等因素的影响，产生误差。工程师利用最小二乘法对多个卫星信号进行加权拟合，提高定位精度。
示例代码：
import numpy as np
# 卫星信号坐标点（模拟）
points = np.array([
[10.1, 10.2],
[10.3, 10.1],
[10.0, 10.4],
[10.2, 10.3]
])
# 最小二乘法求平均位置
mean_x = np.mean(points[:, 0])
mean_y = np.mean(points[:, 1])
print(f"修正后的位置：({mean_x:.2f}, {mean_y:.2f})")游戏AI —— 强化学习中梯度下降法的应用
应用背景：
在游戏中，AI角色需要根据玩家行为做出反应。通过梯度下降法不断调整策略函数，使得AI越来越聪明。
示例代码（简化版）：
# 模拟AI策略函数更新
def update_policy(params, reward, learning_rate=0.01):
return params + learning_rate * reward
params = 0.5
reward = 0.8
for _ in range(100):
params = update_policy(params, reward)
print(f"最终策略参数：{params:.2f}")自动驾驶路径规划 —— 梯度下降法用于轨迹优化
应用背景：
自动驾驶汽车需要实时感知周围环境并做出决策。它使用的大量视觉识别、路径规划模型都依赖梯度下降进行训练。
示例代码（简化）：
import numpy as np
# 路径点（x, y）
path_points = np.array([
[0, 0],
[1, 1],
[2, 2],
[3, 3]
])
# 使用线性回归拟合路径
X = path_points[:, 0].reshape(-1, 1)
y = path_points[:, 1]
model = LinearRegression()
model.fit(X, y)
print(f"拟合路径斜率为：{model.coef_[0]:.2f}")经济学供需曲线建模 —— 最小二乘法的应用
应用背景：
经济学家可以用最小二乘法根据历史数据拟合商品的价格与销量之间的关系，从而预测市场行为。
示例代码：
import numpy as np
# 数据：价格 vs 销量
prices = np.array([10, 20, 30, 40, 50])
sales = np.array([500, 400, 300, 200, 100])
# 最小二乘法拟合
slope, intercept = np.polyfit(prices, sales, 1)
print(f"拟合方程：销量 = {intercept:.2f} - {slope:.2f} × 价格")推荐系统 —— 梯度下降法在协同过滤中的应用
应用背景：
推荐系统背后使用的协同过滤或矩阵分解模型，也常用梯度下降法来优化用户和物品之间的评分预测。
示例代码（简化）：
# 用户A对电影B的打分预测 = 用户偏好 × 电影特征
user_pref = 0.5
movie_feat = 0.7
prediction = user_pref * movie_feat
print(f"预测打分：{prediction:.2f}")总结对比表
| 方法 | 应用场景 | 优点 | 缺点 | 是否需要调参 |
|---|---|---|---|---|
| 线性回归 | 房价预测、教育评估 | 简单高效 | 只适合线性关系 | 否 |
| 最小二乘法 | GPS定位、物理实验 | 数学严谨 | 不适合复杂模型 | 否 |
| 梯度下降法 | 推荐系统、神经网络 | 适用广泛 | 收敛慢、需调参 | 是 |
八、 一句话总结：
我们想用一条直线来预测一件事的结果，比如根据房子面积预测房价。我们先猜一条线，然后一点点调整它，让它尽量贴合已有的数据，这样就能用它来预测新的数据了。
什么是线性回归？
简单理解：
- 你有一组数据，比如房子面积和价格。
- 你想根据面积来预测价格。
- 你发现价格随着面积线性增长（差不多是一条直线）。
- 所以你画一条线，让它尽量靠近这些点，这样就能预测新房子的价格了。
数学公式：
房价 = a × 面积 + b
- a 是斜率（面积对价格的影响）
- b 是截距（基础价格）
什么是“最小二乘法”？
简单理解：
- 我们画的那条线，不可能完美穿过每一个点。
- 有些点在上面，有些在下面。
- 我们把每个点和线的距离平方加起来，看看总误差有多大。
- 我们要找那条线，让这个总误差最小。
类比：
- 就像你用尺子量身高，每次量的误差不一样，你希望平均误差最小。
什么是“梯度下降法”？
简单理解：
- 我们不知道那条“最好的线”在哪。
- 我们先随便画一条线，然后一点点调整它。
- 每次调整的方向是“让误差变小”的方向。
- 一步一步走，最后走到误差最小的地方。
类比：
就像你在山上，看不见路，只能一步一步往“最陡的下坡方向”走，最终走到山谷。
梯度下降是怎么工作的？
- 先猜一个线（a 和 b 的值）
- 算一下误差有多大
- 看看误差是往哪边变小的
- 往那个方向走一小步
- 重复上面几步，直到误差很小
总结三者的关系：
| 方法 | 作用 | 通俗理解 |
|---|---|---|
| 线性回归 | 找一条线来预测结果 | 用一条直线来预测房价 |
| 最小二乘法 | 衡量误差 | 看这条线和数据点差多远 |
| 梯度下降法 | 找最好的线 | 一点点调整线的位置，让误差最小 |
记忆口诀：
线性回归画直线，
最小二乘算误差，
梯度下降调参数，
一步一走找最优！
举个例子：
你有以下数据：
| 面积（㎡） | 房价（万元） |
|---|---|
| 50 | 150 |
| 80 | 240 |
| 100 | 300 |
| 120 | 360 |
| 150 | 450 |
你想预测：面积是 90 平方米的房子值多少钱？
你用线性回归训练出模型：
房价 = 3 × 面积 + 0.12
所以预测：
房价 = 3 × 90 + 0.12 = 270.12 万元
小白总结一句话：
我们用一条直线来学习数据的规律，通过不断调整这条线，让它越来越准，最后用它来预测新数据！