
- 博主简介:努力学习的22级计算机科学与技术本科生一枚🌸
- 博主主页: @Yaoyao2024
- 往期回顾:【AlphaFold3】符号说明+Data_pipline学习笔记
- 每日一言🌼: “去留无意,闲看庭前花开花落;宠辱不惊,漫随天外云卷云舒。”——《幽窗小记》🍃

前言-AF3与AF2比较
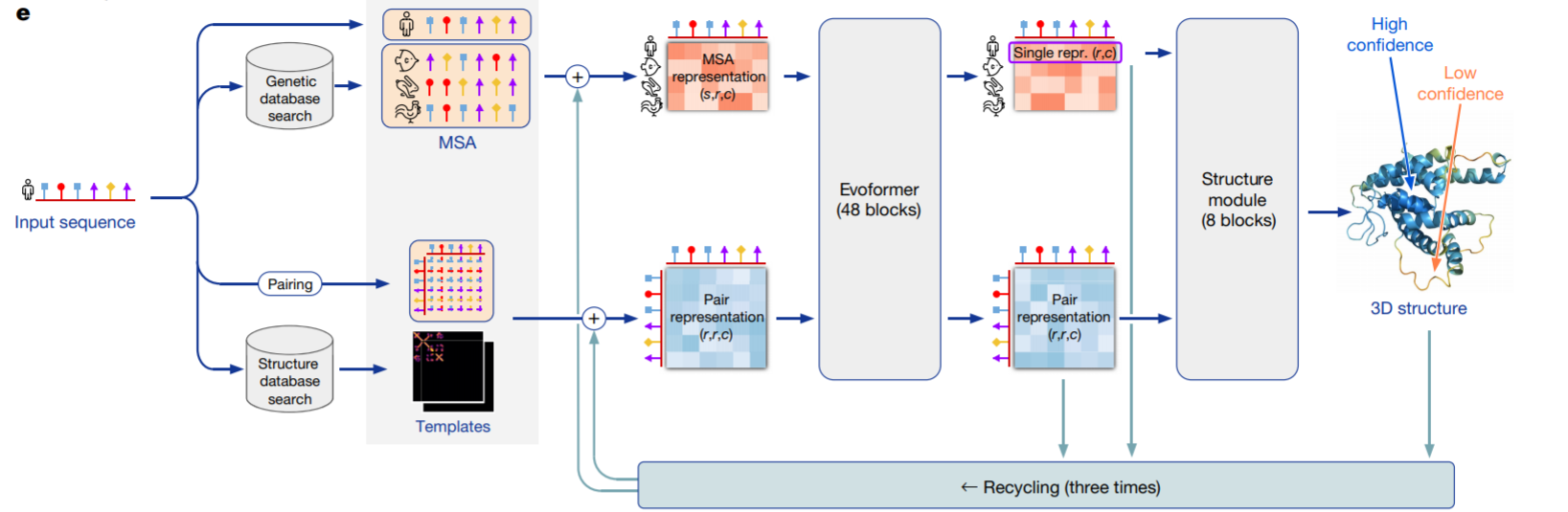
- AlphaFold2架构图
- AlphaFold3架构图
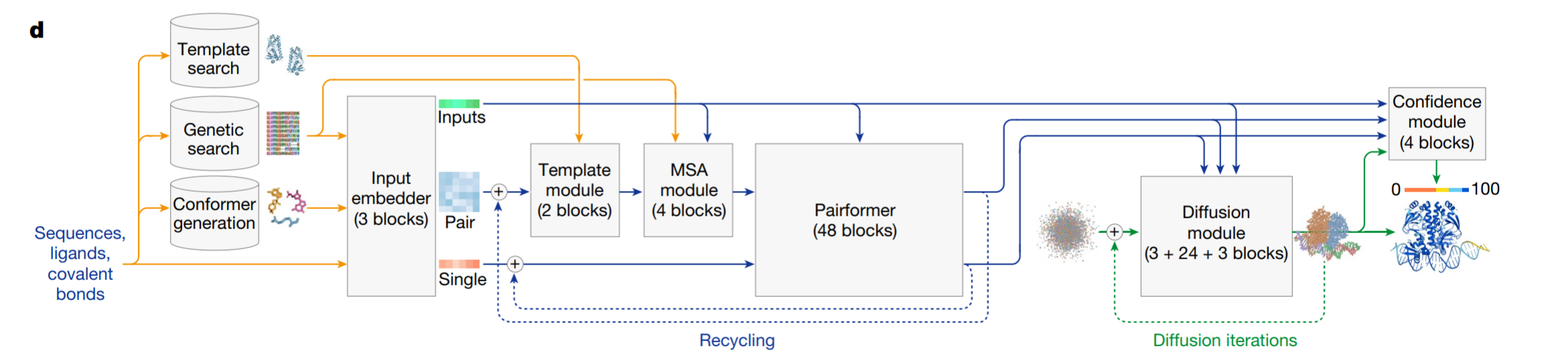
AlphaFold3 在架构和训练流程上的重大革新(相较于 AlphaFold2)主要体现在以下几个方面:
- 通用化学结构的扩展与数据效率提升
- 目标:不仅处理蛋白质,还能适应更广泛的化学分子(如配体、核酸等)。
- 方法:通过架构改进减少对大量训练数据的依赖,提升学习的数据效率(即用更少的数据达到更好的效果)。
- 简化MSA处理:用Pairformer替代Evoformer
- AlphaFold2的局限:依赖复杂的"Evoformer"模块处理多序列比对(MSA)信息,计算成本高。
- AlphaFold3的改进:
- 用更简单的Pairformer模块(图2a)替代Evoformer,减少MSA处理的计算开销。
- Pairformer可能专注于直接处理残基对(pair)的特征,而非MSA的全局演化关系,从而提升效率。
- 扩散模型预测原子坐标
- AlphaFold2的局限:
- 使用"结构模块"预测氨基酸局部坐标系(frames)和侧链二面角(torsion angles),再通过几何约束生成原子坐标。
- 需依赖立体化学损失函数(stereochemical losses)和手工设计的键合模式规则。
- AlphaFold3的革新:
- 直接用扩散模型(diffusion module) 预测原始原子坐标(图2b),无需中间参数化。
- 扩散模型通过逐步去噪生成结构,其多尺度特性(不同噪声水平)自然兼顾全局与局部结构优化:
- 低噪声时,网络专注于局部结构的精细化;
- 高噪声时,调整整体拓扑。
- 优势:
- 无需显式约束立体化学或键合模式(由扩散模型隐式学习);
- 天然支持任意化学组分(如非标准残基、小分子)。
- 训练流程的简化
- 移除手工设计的立体化学损失函数(如键长、键角约束),依赖扩散模型自身生成合理的3D结构。
- 减少对分子类型特异性处理的需求,使模型更通用。
🪧关键创新总结
| 模块 | AlphaFold2 | AlphaFold3 |
|---|---|---|
| MSA处理 | Evoformer(复杂) | Pairformer(简化) |
| 结构生成 | 结构模块(基于几何参数化) | 扩散模型(直接预测坐标) |
| 化学约束 | 显式立体化学损失 | 隐式学习(通过扩散多尺度性) |
| 通用性 | 主要针对蛋白质 | 支持任意化学组分 |
这种改进使得AlphaFold3在保持高精度的同时,扩展了应用范围并降低了计算成本,尤其在处理非蛋白质分子时更具灵活性。扩散模型的引入是结构生物学领域的一次范式转变,将传统基于物理的建模转化为纯数据驱动的生成式方法。
一、Model architecture 模型架构
🪧翻译
该模型架构大体基于AlphaFold 2;但为了让模型能够预测除蛋白质外更广泛的分子,同时进一步提高蛋白质结构预测的准确性,我们做了多项改进。
该模型是一个条件扩散模型(conditional diffusion model),与大多数其他扩散模型不同的是,其大部分计算都发生在条件部分(conditioning)。模型的条件部分在整体架构上与AlphaFold 2的主干(模板模块、MSA模块和Pairformer)相似,但存在多个关键差异。与该架构对应的算法如算法1和主文章图1d所示。我们引入了更通用的tokenization 方案:与AlphaFold 2中一样,每个氨基酸残基对应一个token,每个核苷酸也对应一个token;而对于其他分子,我们将每个重原子编码为一个独立的。为了得到初始的主干输入特征,我们采用了更复杂的token输入特征嵌入器(Inpute feature embedder),它通过对所有原子进行注意力计算来编码所有分子的化学结构信息,最终生成一个表示所有token的单一表征。
给定输入特征后,我们以与AlphaFold 2类似的方式构建成对表征。随后,该成对表征和单表征被输入到条件网络的主体部分,该部分会被循环使用多次。
条件网络的主体部分包含一个与AlphaFold 2风格相似的模板嵌入器(TemplateEmbedder),其作用是将提供的模板信息编码到成对表征中。之后是MSA模块,该模块从多序列比对(MSA)中提取信息并将其编码到成对表征中——这里我们的MSA同时用于蛋白质序列和RNA序列。生成的成对表征随后被用作主Pairformer堆叠(PairformerStack)的输入,该堆叠同时接收单表征作为输入,并对表征进行进一步处理,构成模型的主循环。
生成的单嵌入和成对嵌入随后用于条件化扩散过程。这里的扩散由一个扩散模块(Diffusion Module)参数化,该模块是一个计算成本低得多的子网络,用于编码单一去噪步骤。值得注意的是,其计算量随token数量呈二次方增长,而非三次方。扩散模块的输出结构随后被传入置信头(confidence head),该头结合成对表征、单表征和结构信息,提供置信度度量。模型的各组件将在后续章节中详细描述。

讲解
该流程展示了模型从输入到输出的完整推理步骤,核心逻辑包括:
- 特征嵌入(步骤1-5):生成初始的单表征和成对表征,融入相对位置、键信息等关键特征;
- 多轮循环处理(步骤7-14):通过TemplateEmbedder、MSA模块和PairformerStack反复迭代,逐步提炼结构信息(类似人类反复思考优化方案);
- 结构生成与置信度预测(步骤15-18):扩散模块生成原子坐标,置信头输出pplddt(预测置信度)、距离图等,评估预测可靠性。
一、输入符号与核心符号含义
算法的输入、超参数及核心符号均服务于“将原始特征转化为结构预测结果”的目标,具体含义如下:
1. 输入符号
- f ∗ \mathbf{f}^{*} f∗:表示所有输入特征的集合,对应表5中列出的全部输入特征,包括但不限于:
- token特征(如
restype、asym_id、is_protein/ligand等,描述token的分子类型、链身份等); - 参考特征(如
ref_pos、ref_element等,描述分子的化学结构参考信息); - MSA特征(如
msa、profile等,提供进化信息); - 模板特征(如
template_restype、template_distogram等,提供已知结构参考); - 键特征(如
token_bonds,描述令牌间的成键关系)。
- token特征(如
这些特征是模型推理的“原始素材”,涵盖分子的序列、化学、进化及结构参考信息。
N c y c l e = 4 , N_{\mathbf{cycle}}=4, Ncycle=4,:超参数,指主循环的迭代次数(4次)。循环的目的是通过多次信息提炼,逐步优化单表征和成对表征(类似人类反复思考完善方案)。
c s = 384 c_{\mathrm{s}}=384 cs=384:超参数,单表征(single representation)的维度(384维),用于描述单个令牌的特征向量。
c 2 = 128 c_{2}=128 c2=128:超参数,成对表征(pair representation)的维度(128维),用于描述两个token间的关系特征。
2. 算法中核心符号
{ s i i n p u t s } \{\mathbf{s}_i^{\mathrm{inputs}}\} {siinputs}:输入特征嵌入器(InputFeatureEmbedder)的输出,即“初始单输入表征”。其中
i表示第i个令牌(token), { s i i n p u t s } \{\mathbf{s}_i^{\mathrm{inputs}}\} {siinputs}是一个集合,包含所有令牌的初始单输入特征(融合了化学结构、序列等信息)。s i i n i t \mathbf{s}_i^\mathrm{init} siinit:初始单表征(initial single representation)。通过
LinearNoBias(无偏置线性变换)处理 s i i n p u t s \mathbf{s}_{i}^{\mathrm{inputs}} siinputs得到,维度为 ∈ R c s \in\mathbb{R}^{c_s} ∈Rcs(384维),是描述单个token的基础特征向量。z i j i n i t \mathrm{z}_{ij}^{\mathrm{init}} zijinit:初始成对表征(initial pair representation)。通过对第
i个和第j个令牌的 s i n p u t s s^{inputs} sinputs分别做线性变换后相加得到,维度为 ∈ R c z \in\mathbb{R}^{c_z} ∈Rcz(128维)。其中i和j表示token对(i与j可相同),用于描述两个token间的关系(如空间距离、相互作用)。RelativePositionEncoding ( { f ∗ } ) \text{RelativePositionEncoding}(\{\mathbf{f}^*\}) RelativePositionEncoding({f∗}):相对位置编码,基于输入特征中的位置信息(如
residue_index、token_index)生成,用于向 z i j i n i t \mathbf{z}_{ij}^{\mathrm{init}} zijinit注入token间的相对位置关系(如序列上的远近、链内/链间位置)。f i j token − b o n d s \mathrm{f}_{ij}^{\textbf{token}_{-}\mathbf{bonds}} fijtoken−bonds:键特征(来自表5的
token_bonds),表示tokeni和j是否存在化学键(如聚合物-配体键、配体间键)。通过LinearNoBias变换后加入 z i j i n i t \mathbf{z}_{ij}^{\mathrm{init}} zijinit,使成对表征包含化学成键信息。{ z ^ i j } , { s ^ i } \{\hat{\mathbf{z}}_{ij}\},\{\hat{\mathbf{s}}_i\} {z^ij},{s^i}:中间变量,分别存储上一轮循环输出的成对表征和单表征,初始化为0。 { z ^ i j } \{\hat{\mathbf{z}}_{ij}\} {z^ij}对应上一轮的成对关系特征, { s ^ i } \{\hat{\mathbf{s}}_i\} {s^i}对应上一轮的单个token特征。 z i j ∈ R c z \mathbf{z}_{ij}\in\mathbb{R}^{c_{\mathrm{z}}} zij∈Rcz
z i j \mathbf{z}_{ij} zij:第
c轮循环中的成对表征。由 z i j i n i t \mathbf{z}_{ij}^{\mathrm{init}} zijinit(初始成对表征)与上一轮中间成对表征 z i j i n i t \mathbf{z}_{ij}^{\mathrm{init}} zijinit的层归一化(LayerNorm)+线性变换结果相加得到,是本轮循环中用于传递令牌间关系的核心特征。s i \mathbf{s}_{i} si:第
c轮循环中的单表征。由 s i i n i t \mathbf{s}_i^{\mathrm{init}} siinit(初始单表征)与上一轮中间单表征 s ^ i \hat{\mathbf{s}}_{i} s^i的层归一化+线性变换结果相加得到,是本轮循环中用于传递单个token特征的核心向量。 s i ∈ R c s \mathbf{s}_i\in\mathbb{R}^{c_s} si∈Rcs{ x ⃗ l p r e d } \{\vec{\mathbf{x}}_l^\mathrm{pred}\} {xlpred}:预测的原子坐标集合。
l表示扩散采样的步骤或批次,向量 x ⃗ l p r e d \vec{\mathbf{x}}_{l}^{\mathrm{pred}} xlpred包含每个原子的三维空间坐标(单位Å),由扩散模块(Diffusion Module)生成。{ p l p l d d t } , { p i j p a e } , { p i j p d e } , { p l r e s o l v e d } \{\mathbf{p}_l^{\mathrm{plddt}}\},\{\mathbf{p}_{ij}^{\mathrm{pae}}\},\{\mathbf{p}_{ij}^{\mathrm{pde}}\},\{\mathbf{p}_l^{\mathrm{resolved}}\} {plplddt},{pijpae},{pijpde},{plresolved}:置信头(Confidence Head)的输出:
- p l p l d d t \mathbf{p}_l^{\mathbf{plddt}} plplddt:预测的LDDT(局部距离差异测试)值,衡量结构预测的可靠性;
- p i j p a e \mathbf{p}_{ij}^{\mathbf{pae}} pijpae/ p i j p d e \mathbf{p}_{ij}^{\mathrm{pde}} pijpde:成对原子误差(如蛋白质原子对、核酸原子对),描述令牌
i和j的原子距离预测误差; - p l r e s o l v e d \mathbf{p}_l^{\mathrm{resolved}} plresolved:预测的“已解析”状态,指示原子坐标的可信度(类似实验解析中的“已解析残基”)。
p i j distogram \mathrm{p}_{ij}^{\text{distogram}} pijdistogram:距离图头(Distogram Head)的输出,是令牌
i和j的原子间距离分布(离散为39个区间),用于辅助评估结构的空间合理性。
二、算法对应的模块及实现
算法的每一步对应模型架构中的特定模块,整体实现了“从原始特征到结构预测及置信度评估”的完整流程,具体对应关系如下:
1. 步骤1:输入特征嵌入 { s i i n p u t s } = InputFeatureEmbedder ( { f ∗ } ) \{\mathbf{s}_i^{\mathrm{inputs}}\}=\text{InputFeatureEmbedder}(\{\mathbf{f}^*\}) {siinputs}=InputFeatureEmbedder({f∗})
- 对应模块:输入特征嵌入器(InputFeatureEmbedder)。
- 功能:将输入特征集合 { f ∗ } \{\mathbf{f}^*\} {f∗}(序列、化学、进化等信息)通过注意力机制编码为初始单输入表征 { s i i n p u t s } \{\mathrm{s}_i^{\mathrm{inputs}}\} {siinputs}。
- 实现:对所有原子的特征(如
ref_element、ref_charge、msa)进行全局注意力计算,融合化学结构(如原子类型、电荷)和序列信息,生成每个token的统一初始特征向量 { s i i n p u t s } \{\mathbf{s}_i^{\mathrm{inputs}}\} {siinputs}。
2. 步骤2-5:初始表征构建( s i i n i t , z i j i n i t \mathrm{s_i^{init}}, \mathrm{z_{ij}^{init}} siinit,zijinit的生成)
- 对应模块:特征初始化模块(含线性变换、相对位置编码注入)。
- 功能:基于 { s i i n p u t s } \{\mathbf{s}_i^{\mathrm{inputs}}\} {siinputs}构建初始单表征和成对表征,注入位置和键信息。
- 实现:
- 步骤2:通过无偏置线性变换将 s i i n p u t s \mathbf{s}_i^{\mathrm{inputs}} siinputs映射为384维的 s i i n i t \mathrm{s}_i^{\mathrm{init}} siinit(单表征基础);
- 步骤3:通过两个无偏置线性变换分别处理 s i i n p u t s \mathbf{s}_{i}^{\mathrm{inputs}} siinputs和 s j i n p u t s \mathbf{s}_{j}^{\mathrm{inputs}} sjinputs,相加得到128维的 z i j i n i t \mathbf{z}_{ij}^{\mathrm{init}} zijinit(成对表征基础);
- 步骤4-5:向 z i j i n i t \mathbf{z}_{ij}^{\mathrm{init}} zijinit中加入相对位置编码和键特征,使其包含token间的空间位置和化学成键关系。
3. 步骤7-14:主循环(Ncycle=4次迭代)
核心逻辑:通过多轮迭代,利用条件网络的核心模块(模板嵌入器、MSA模块、Pairformer堆叠)反复提炼信息,优化单表征和成对表征。
步骤8-9: z i j \mathbf{z}_{ij} zij更新 + 模板嵌入( { z i j } + = TemplateEmbedder ( { f ∗ } , { z i j } ) \{\mathbf{z}_{ij}\}+=\text{TemplateEmbedder}(\{\mathbf{f}^*\},\{\mathbf{z}_{ij}\}) {zij}+=TemplateEmbedder({f∗},{zij}))
- 对应模块:模板嵌入器(TemplateEmbedder)。
- 功能:将模板特征(如
template_restype、template_distogram)编码到成对表征 z i j z_{ij} zij中,注入已知结构的参考信息。 - 实现:通过注意力机制将模板的结构关系(如模板中令牌
i和j的距离)融合到 z i j z_{ij} zij,增强成对表征的结构参考价值。
步骤10:MSA模块处理 { z i j } + = MsaModule ( { f S i m s a } , { z i j } , { s i i n p u t s } ) \{\mathbf{z}_{ij}\}+=\text{MsaModule}(\{\mathbf{f}_{Si}^{\mathrm{msa}}\},\{\mathbf{z}_{ij}\},\{\mathbf{s}_i^{\mathrm{inputs}}\}) {zij}+=MsaModule({fSimsa},{zij},{siinputs})
- 对应模块:MSA模块(MSA Module)。
- 功能:从MSA特征(如
msa、profile)中提取进化信息(如同源序列的保守性、变异模式),编码到 z i j z_{ij} zij中。 - 实现:对蛋白质和RNA的MSA进行注意力计算,将同源序列中令牌
i和j的共变异关系转化为成对表征的更新,增强模型对进化约束的学习。
步骤11-12:单表征更新 + Pairformer堆叠处理( { s i } , { z i j } = PairformerStack ( { s i } , { z i j } ) \{\mathbf{s}_i\},\{\mathbf{z}_{ij}\}=\text{PairformerStack}(\{\mathbf{s}_i\},\{\mathbf{z}_{ij}\}) {si},{zij}=PairformerStack({si},{zij}))
- 对应模块:Pairformer堆叠(PairformerStack)。
- 功能:模型的核心处理模块,通过多轮注意力机制(类似AlphaFold 2的Evoformer,但更简洁)同时优化单表征和成对表征,捕捉令牌的局部结构和全局相互作用。
- 实现:堆叠包含多个Pairformer块,每个块通过“自注意力”更新单表征( s i s_i si)、通过“成对注意力”更新成对表征( z i j z_{ij} zij),反复传递空间和化学信息(如配体与蛋白质的结合口袋特征、核酸的碱基配对)。
步骤13:中间结果保存( { s ^ i } , { z ^ i j } ← { s i } , { z i j } \{\hat{\mathbf{s}}_i\},\{\hat{\mathbf{z}}_{ij}\}\leftarrow\{\mathbf{s}_i\},\{\mathbf{z}_{ij}\} {s^i},{z^ij}←{si},{zij})
- 功能:将本轮优化后的单表征和成对表征保存为下一轮的输入,实现“迭代精炼”。
4. 步骤15:扩散采样: { x ⃗ l p r e d } = SampleDiffusion ( { f ∗ } , { s i i n p u t s } , { s i } , { z i j } ) \{\vec{\mathbf{x}}_l^{\mathbf{pred}}\}=\text{SampleDiffusion}(\{\mathbf{f}^*\},\{\mathbf{s}_i^{\mathrm{inputs}}\},\{\mathbf{s}_i\},\{\mathbf{z}_{ij}\}) {xlpred}=SampleDiffusion({f∗},{siinputs},{si},{zij})
- 对应模块:扩散模块(Diffusion Module)。
- 功能:以条件网络输出的 { f ∗ } , { s i i n p u t s } , { s i } , { z i j } \{\mathbf{f}^{*}\},\{\mathbf{s}_{i}^{\mathrm{inputs}}\},\{\mathbf{s}_{i}\},\{\mathbf{z}_{ij}\} {f∗},{siinputs},{si},{zij}作为为条件,通过扩散过程(逐步去噪)生成最终的原子坐标。
- 实现:从随机高斯噪声分布出发,利用扩散模块(参数化单步去噪函数) s i s_i si(单令牌特征)和 z i j z_{ij} zij(令牌间关系)的引导下,逐步优化原子位置,最终输出 { x ⃗ l p r e d } \{\vec{\mathbf{x}}_{l}^{\mathrm{pred}}\} {xlpred}。其计算量随令牌数呈二次增长(而非三次),高效适配多原子分子(如配体)。
5. 步骤16:置信度评估( C o n f i d e n c e H e a d ( { s i i n p u t s } , { s i } , { z i j } , { x ⃗ l p r e d } ) \mathrm{ConfidenceHead}(\{\mathbf{s}_{i}^{\mathrm{inputs}}\},\{\mathbf{s}_{i}\},\{\mathbf{z}_{ij}\},\{\vec{\mathbf{x}}_{l}^{\mathrm{pred}}\}) ConfidenceHead({siinputs},{si},{zij},{xlpred}))
- 对应模块:置信头(Confidence Head)。
- 功能:结合单表征、成对表征和预测结构,输出模型对预测结果的可靠性评估。
- 实现:通过注意力机制融合 s i n p u t s i {sinputs_i} sinputsi(初始特征)、 s i {s_i} si(优化后单表征)、 z i j {z_{ij}} zij(优化后成对表征)和 { x ⃗ l p r e d } \{\vec{\mathbf{x}}_{l}^{\mathrm{pred}}\} {xlpred}(原子坐标),预测
pplddt等置信度指标。
6. 步骤17:距离图生成( p i j d i s t o g r a m = D i s t o g r a m H e a d ( z i j ) \mathbf{p}_{ij}^{\mathrm{distogram}}=\mathrm{DistogramHead}(\mathbf{z}_{ij}) pijdistogram=DistogramHead(zij))
- 对应模块:距离图头(Distogram Head)。
- 功能:基于成对表征 z i j z_{ij} zij预测令牌间的原子距离分布,辅助验证结构的空间合理性。
- 实现:通过线性变换和softmax激活,将 z i j z_{ij} zij(128维)映射为39个距离区间的概率分布(对应表5中
template_distogram的离散方式)。
三、总结
Algorithm 1通过“特征嵌入→初始表征构建→多轮迭代精炼→扩散生成→置信度评估”的流程,实现了从原始分子信息到结构预测的完整推理。核心逻辑是:以输入特征为基础,通过4次循环迭代(Ncycle=4),利用模板嵌入器、MSA模块和Pairformer堆叠逐步优化单表征和成对表征(捕捉分子的化学、进化和结构信息),最终通过扩散模块生成原子坐标,并输出置信度指标。
符号设计上,i/j聚焦“单个令牌”和“令牌对”的细节,Ncycle控制信息提炼的深度,cs/cz平衡表征的信息容量与计算效率;模块实现上,各步骤紧密衔接,形成“输入→处理→输出”的闭环,既保留了AlphaFold 2的进化信息处理优势,又通过通用令牌化和扩散模块适配了多分子类型预测。