
文章目录
1.研究背景与动机
在计算机视觉领域,特征提取对各类任务性能至关重要。传统卷积神经网络(CNNs) 擅长捕捉 局部模式且复杂度线性增长,但全局上下文建模能力较弱;视觉 Transformer(ViTs)具备全局感受野,却因与输入大小相关的二次复杂度限制了在效率敏感的下游任务(如检测、分割)中的应用。基于状态空间模型(SSMs)的方法(如 Mamba、VMamba)结合了全局感受野与线性复杂度的优势,但为适配图像非因果性采用的多扫描策略存在计算冗余,且在参数受限时易出现 “长距离遗忘问题”(远距离特征贡献衰减)。
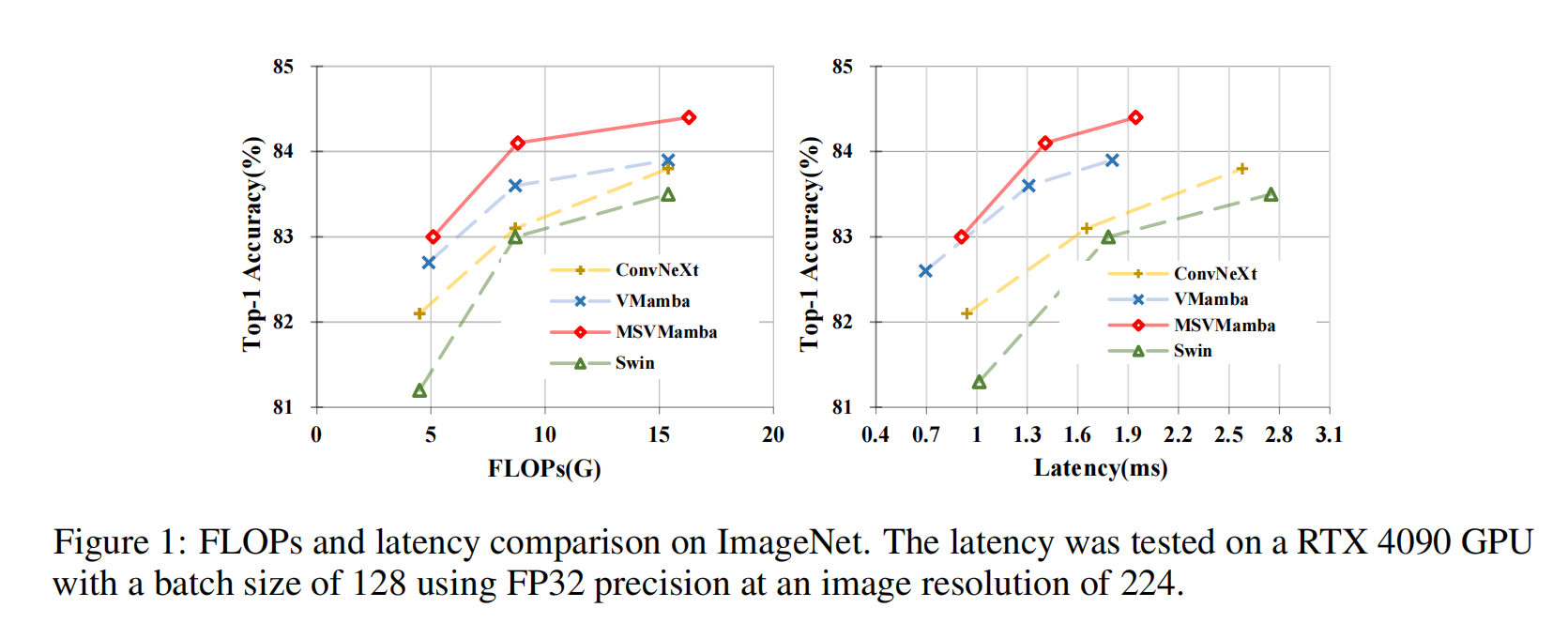
研究核心目标是:在有限参数下,缓解 SSMs 的长距离遗忘问题,减少计算冗余,实现效率与性能的更好权衡。
2. 核心方法
2.1 预备知识:mamba-ssm
状态空间模型:经典的状态空间模型(SSMs)表示一个连续系统,它将输入序列 x ( t ) ∈ R L x(t) \in \mathbb{R}^{L} x(t)∈RL映射到 latent 空间表示 h ( t ) ∈ R N h(t) \in \mathbb{R}^{N} h(t)∈RN,然后基于该表示预测输出序列 y ( t ) ∈ R L y(t) \in \mathbb{R}^{L} y(t)∈RL。从数学上讲,SSM可描述为:
h ′ ( t ) = A h ( t ) + B x ( t ) , y ( t ) = C h ( t ) \begin{equation} h'(t) = A h(t) + B x(t), \quad y(t) = C h(t) \end{equation} h′(t)=Ah(t)+Bx(t),y(t)=Ch(t)
其中 A ∈ R N × N A \in \mathbb{R}^{N ×N} A∈RN×N、 B ∈ R N × 1 B \in \mathbb{R}^{N ×1} B∈RN×1和 C ∈ R 1 × N C \in \mathbb{R}^{1 ×N} C∈R1×N是可学习参数。
离散化:为了使连续状态空间模型(SSMs)适用于深度学习框架,实现离散化操作至关重要。通过引入时间尺度参数 Δ ∈ R \Delta \in \mathbb{R} Δ∈R并采用广泛使用的零阶保持(ZOH)作为离散化规则,可以推导出A和B的离散化版本(分别表示为 A ‾ \overline{A} A和 B ‾ \overline{B} B),据此,式1可重写为离散形式:
h ( t ) = A ‾ h ( t − 1 ) + B ‾ x ( t ) , y ( t ) = C h ( t ) , where A ‾ = e Δ A , B ‾ = ( Δ A ) − 1 ( e Δ A − I ) Δ B ≈ Δ B \begin{equation} \begin{aligned} h(t) &= \overline{A} h(t-1) + \overline{B} x(t), \quad y(t) = C h(t), \\ \text{where } \overline{A} &= e^{\Delta A}, \quad \overline{B} = (\Delta A)^{-1} \left(e^{\Delta A} - I\right) \Delta B \approx \Delta B \end{aligned} \end{equation} h(t)where A=Ah(t−1)+Bx(t),y(t)=Ch(t),=eΔA,B=(ΔA)−1(eΔA−I)ΔB≈ΔB
离散化的详细推导可见这篇文章
其中 I I I表示单位矩阵。之后,式2的过程可以通过全局卷积的方式实现:
y = x ⊙ K ‾ , K ‾ = ( C B ‾ , C A ‾ B ‾ , … , C A ‾ L − 1 B ‾ ) \begin{equation} y = x \odot \overline{K}, \quad \overline{K} = \left(C \overline{B},\; C \overline{A} \overline{B},\; \dots,\; C \overline{A}^{L-1} \overline{B}\right) \end{equation} y=x⊙K,K=(CB,CAB,…,CAL−1B)
该式直接迭代带入即可得到
其中 x ∈ R 1 × L x \in \mathbb{R}^{1 × L} x∈R1×L是输入序列, K ‾ ∈ R L × 1 \overline{K} \in \mathbb{R}^{L × 1} K∈RL×1是卷积核。
选择性状态空间模型:Mamba引入的选择性状态空间 S 6 S6 S6机制使参数 B ‾ \overline{B} B、 C ‾ \overline{C} C和 Δ Δ Δ依赖于输入,从而提升了基于SSM的模型的性能。在使 B ‾ \overline{B} B、 C ‾ \overline{C} C和 Δ Δ Δ依赖于输入后,式3中的全局卷积核可重写为:
K ‾ = ( C L B ‾ L , C L A ‾ L − 1 B ‾ L − 1 , … , C L ∏ i = 1 L − 1 A ‾ i B ‾ 1 ) \begin{equation} \overline{K} = \left( C_{L} \overline{B}_{L},\; C_{L} \overline{A}_{L-1} \overline{B}_{L-1},\; \dots,\; C_{L} \prod_{i=1}^{L-1} \overline{A}_{i} \overline{B}_{1} \right) \end{equation} K=(CLBL,CLAL−1BL−1,…,CLi=1∏L−1AiB1)
2.2 多扫描策略分析
使用 S 6 S6 S6块处理图像数据时,2D特征图 Z ∈ R H × W × D Z \in \mathbb{R}^{H ×W ×D} Z∈RH×W×D被展平为图像令牌的1D序列,表示为 X ∈ R L × D X \in \mathbb{R}^{L ×D} X∈RL×D。根据式4和式2, S 6 S6 S6中第 m m m个令牌对第 n n n个令牌 ( m < n ) (m<n) (m<n)构建的贡献可表示为:
C n ∏ i = m n A ‾ i B ‾ m = C n A ‾ ( m → n ) B ‾ m , w h e r e A ‾ ( m → n ) = e ∑ i = m n Δ i A \begin{equation} C_{n} \prod_{i=m}^{n} \overline{A}_{i} \overline{B}_{m}=C_{n} \overline{A}_{(m \to n)} \overline{B}_{m} , where \overline{A}_{(m \to n)}=e^{\sum_{i=m}^{n} \Delta_{i} A} \end{equation} Cni=m∏nAiBm=CnA(m→n)Bm,whereA(m→n)=e∑i=mnΔiA
通常,学习到的 Δ i A \Delta_{i} A ΔiA为负值,这使模型倾向于优先考虑近期令牌的信息。因此,随着序列长度的增加,式5中的指数项 e ∑ i = m n Δ i A e^{\sum_{i=m}^{n} \Delta_{i} A} e∑i=mnΔiA会显著衰减,导致远距离令牌的贡献微乎其微。此外, S 6 S6 S6块的因果特性确保信息只能在令牌之间单向传播,阻止早期令牌获取后续令牌的信息。
图像固有的非因果特性使得 S 6 S6 S6块直接应用于视觉相关任务时效果欠佳。为了缓解这一局限性,ViM和VMamba引入了通过多个方向扫描图像特征然后融合这些特征的方法。一般来说,沿着某一扫描路径更新的令牌,表示为 S c a n ( Z ( p , q ) ) Scan(Z_{(p, q)}) Scan(Z(p,q))(其中 ( p , q ) (p, q) (p,q)表示坐标),可通过下式获得:
S c a n ( Z ( p , q ) ) = C α ∑ i = 1 α A ‾ ( i → α ) B ‾ i σ ( Z ) i . \begin{equation} \begin{array} {r}{Scan\left(Z_{(p,q)}\right) =C_{\alpha }\sum _{i=1}^{\alpha }\overline {A}_{(i\to \alpha )}\overline {B}_{i}\sigma (Z)_{i}.}\end{array} \end{equation} Scan(Z(p,q))=Cα∑i=1αA(i→α)Biσ(Z)i.
式6可由式5累加得到
在式6中, σ \sigma σ表示将2D特征图转换为1D序列的变换,α表示 Z ( p , q ) Z(p, q) Z(p,q)在变换后的1D序列中的对应索引。之后,多扫描路径的结果相加,生成增强特征 Z ′ ( p , q ) Z'(p, q) Z′(p,q),可表示为:
Z ( p , q ) ′ = ∑ k S c a n k ( Z ( p , q ) ) = ∑ k C α k ∑ i = 1 α k A ‾ ( i → α k ) B ‾ i σ k ( Z ) i \begin{equation} Z_{(p, q)}'=\sum_{k} Scan_{k}\left(Z_{(p, q)}\right)=\sum_{k} C_{\alpha_{k}} \sum_{i=1}^{\alpha_{k}} \overline{A}_{\left(i \to \alpha_{k}\right)} \overline{B}_{i} \sigma_{k}(Z)_{i} \end{equation} Z(p,q)′=k∑Scank(Z(p,q))=k∑Cαki=1∑αkA(i→αk)Biσk(Z)i
这种多扫描策略允许令牌相互获取信息。在ViM中,两个不同的扫描路径对应式6中的两种不同变换,具体来说,是展平变换和带翻转的展平变换。类似地,VMamba通过结合水平和垂直扫描方向扩展了基本的双向扫描,产生了四个不同的扫描路径。此外,多扫描策略还通过最小化令牌之间的有效距离来缓解长距离遗忘问题。对于坐标为 ( p 1 , q 1 ) (p_{1}, q_{1}) (p1,q1)和 ( p 2 , q 2 ) (p_{2}, q_{2}) (p2,q2)的令牌,该策略采用多个扫描路径,每个路径都可能改变它们的相对位置。这些路径中的最小距离由 m i n i k d k ( ( p 1 , q 1 ) → ( p 2 , q 2 ) ) min i_{k} d_{k}((p_{1}, q_{1}) \to (p_{2}, q_{2})) minikdk((p1,q1)→(p2,q2))给出,其中 d k d_{k} dk表示第 k k k次扫描生成的序列中令牌之间的距离。通过减小这一距离,多扫描策略减少了远距离令牌之间影响的衰减,从而增强了模型维持和利用长距离信息的能力。
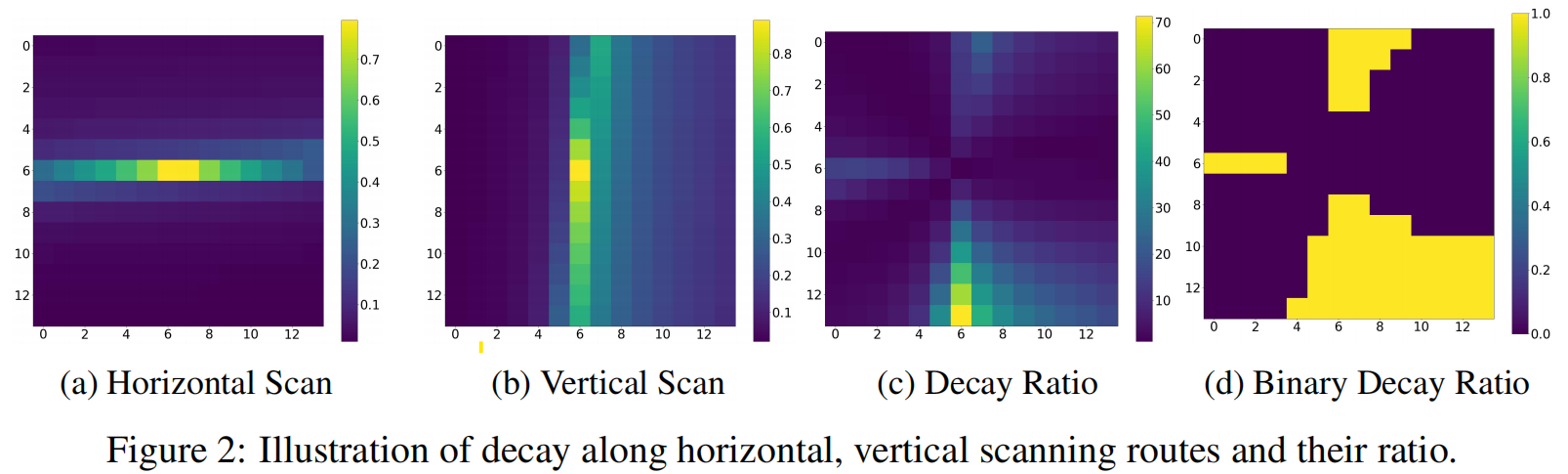
为了更直观地展示多扫描策略与长距离衰减之间的关系,在图2a和图2b中可视化了VMamba-Tiny中沿着水平和垂直扫描方向、相对于中心令牌的指数项 e ∑ i = 1 ∞ Δ i A e^{\sum_{i=1}^{\infty} \Delta_{i} A} e∑i=1∞ΔiA。(这个可视化图在垂直和水平出现差异的原因是数据集中图片的纹理整体成垂直状态)
根据这些观察结果,VMamba中多扫描策略的成功可归因于它缓解了图像数据的非因果特性并减轻了长距离遗忘问题。然而,随着扫描路径数量的增加,计算成本也线性上升,带来了计算冗余。在图2c中,我们展示了图2a与图2b的最大比值,反之亦然。而在图2d中,我们呈现了图2c的二值化版本,应用了10的阈值,其覆盖了整个图的40%以上。这种现象表明,不同扫描路径的衰减率存在差异,导致某些路径在衰减动态中占主导地位,这也可归因于长距离遗忘问题。主导扫描路径的存在意味着某些扫描对信息保留的贡献明显大于其他扫描,这导致多扫描策略中出现计算冗余。
2.3 多尺度2D扫描
缓解长距离遗忘问题最直接有效的方法是缩短序列长度,这可以通过对特征图进行下采样来实现。然而,将所有扫描路径都置于下采样特征图上可能会导致细粒度特征的丢失和下游任务性能的下降。通过对不同扫描的可视化,发现不同扫描路径的衰减率可能不同,这促使我们开发多扫描的层级设计。
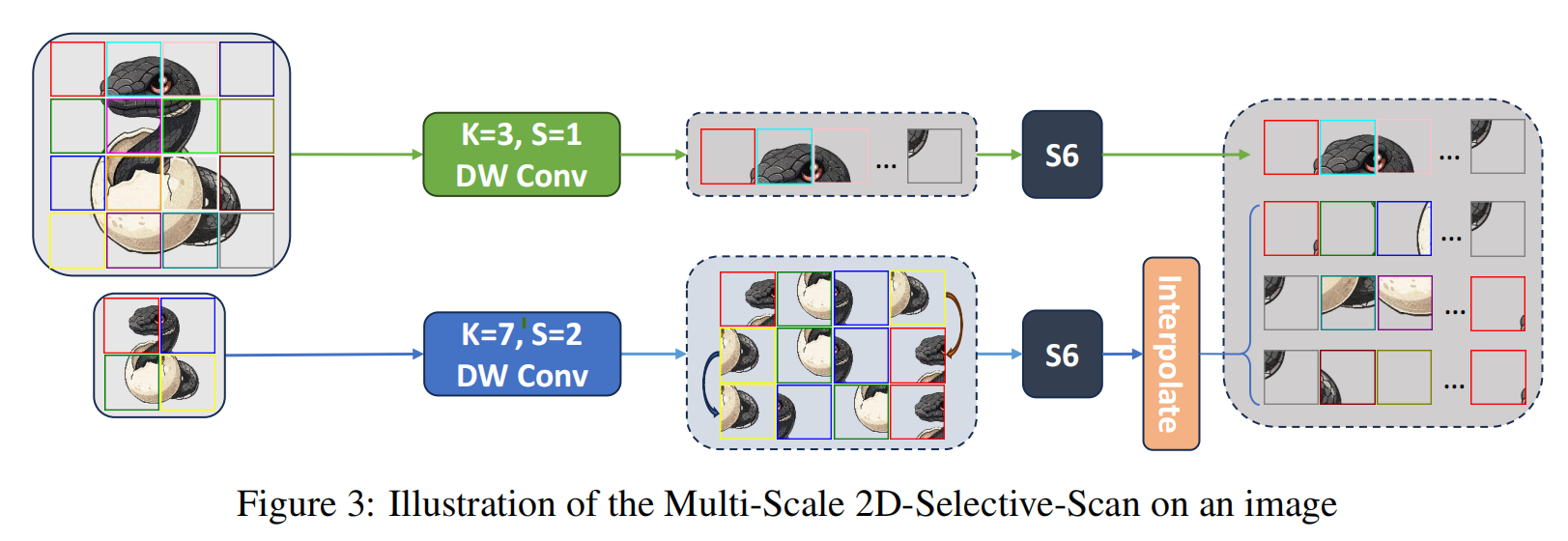
提出了一种简单而有效的多尺度2D(MS2D)扫描策略,如图3所示。我们的方法首先通过应用具有不同步长值的深度卷积(DWConv)生成不同尺度的层级特征图。然后,这些多尺度特征图通过VMamba中的四个不同扫描路径进行处理。具体来说,我们使用步长为 1 1 1和 s s s的DWConv来获得特征图 Z 1 ∈ R H × W × D Z_{1} \in \mathbb{R}^{H ×W ×D} Z1∈RH×W×D和 Z 2 ∈ R H s × W s × D Z_{2} \in \mathbb{R}^{\frac{H}{s} ×\frac{W}{s} ×D} Z2∈RsH×sW×D。之后, Z 1 Z_{1} Z1和 Z 2 Z_{2} Z2通过两个 S 6 S6 S6块进行处理:
Y 1 = S 6 ( σ 1 ( Z 1 ) ) , \begin{equation} Y_{1}=S 6\left(\sigma_{1}\left(Z_{1}\right)\right), \end{equation} Y1=S6(σ1(Z1)),
[ Y 2 , Y 3 , Y 4 ] = S 6 ( [ σ 2 ( Z 2 ) , σ 3 ( Z 2 ) , σ 4 ( Z 2 ) ] ) \begin{equation} \left[Y_{2}, Y_{3}, Y_{4}\right]=S 6\left(\left[\sigma_{2}\left(Z_{2}\right), \sigma_{3}\left(Z_{2}\right), \sigma_{4}\left(Z_{2}\right)\right]\right) \end{equation} [Y2,Y3,Y4]=S6([σ2(Z2),σ3(Z2),σ4(Z2)])
其中 σ \sigma σ是SS2D中使用的将2D特征图转换为1D序列的变换, Y Y Y是处理后的序列。这些处理后的序列被转换回2D特征图,下采样的特征图通过插值进行融合:
Z i ′ = γ i ( Y i ) , i ∈ { 1 , 2 , 3 , 4 } \begin{equation} Z_{i}'=\gamma_{i}\left(Y_{i}\right), i \in\{1,2,3,4\} \end{equation} Zi′=γi(Yi),i∈{1,2,3,4}
Z ′ = Z 1 ′ + I n t e r p o l a t e ( ∑ ( Z j ′ ) ) , j ∈ { 2 , 3 , 4 } \begin{equation} Z'=Z_{1}'+Interpolate\left(\sum\left(Z_{j}'\right)\right), j \in\{2,3,4\} \end{equation} Z′=Z1′+Interpolate(∑(Zj′)),j∈{2,3,4}
其中 γ γ γ是 σ \sigma σ的逆变换, Z ′ Z' Z′是经过MS2D增强的特征图。下采样操作将序列长度减少 s 2 s^{2} s2倍,这也将式5中令牌之间的距离缩短 s 2 s^{2} s2倍,从而缓解长距离遗忘问题。由于单个 S 6 S6 S6块的计算复杂度为 O ( 9 L D N ) O(9 L D N) O(9LDN)(其中N表示SSM维度),用MS2D替代SS2D将四次扫描的总序列长度从 4 L 4 L 4L减少到 ( 1 + 3 / s 2 ) L (1+3 / s^{2}) L (1+3/s2)L,从而提高了效率。在实际应用中,下采样率设为2。值得注意的是,来自 Z 2 Z_{2} Z2的序列通过同一个 S 6 S6 S6块处理。这种方法与为不同扫描路径使用多个 S 6 S6 S6块相比,在保持相同精度的同时有效减少了参数数量。
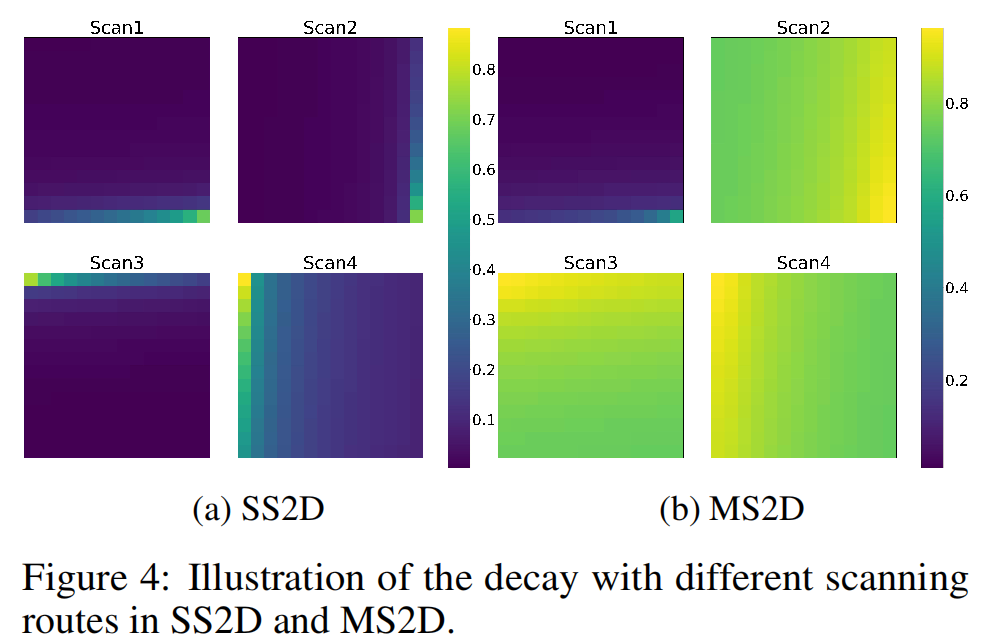
为了更好地说明长距离遗忘问题得到缓解,我们还提供了实证证据,如图4所示。我们比较了VMamba的SS2D和我们的MS2D中沿着扫描路径的衰减,重点关注与图2配置相同的最后一个令牌。下采样特征中的衰减图被插值回去。可以观察到,下采样图中沿着扫描路径的衰减率显著降低,增强了捕捉全局信息的能力。
2.4 整体模型架构
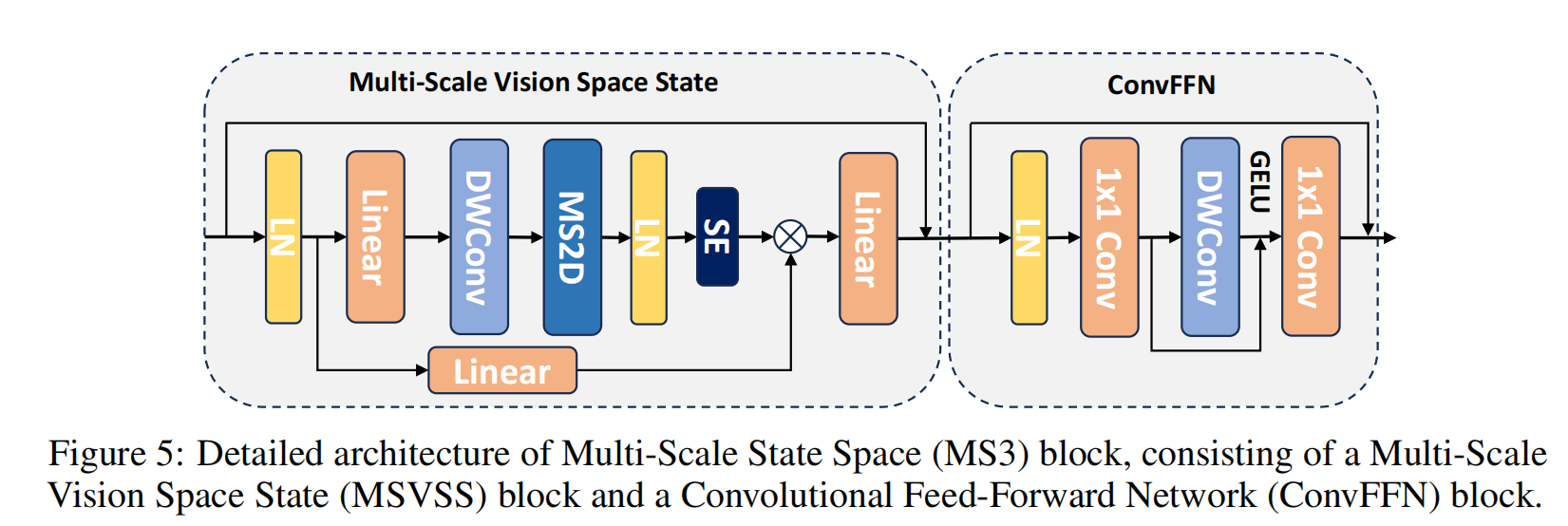
在本研究中,我们通过用多尺度状态空间(MS3)块替代VMamba框架的VSS块来扩展其能力。MS3块的架构框架如图5所示,包括多尺度视觉空间状态(MSVSS)组件和卷积前馈网络(ConvFFN)。MSVSS组件通过调整VMamba中的视觉状态空间框架、用MS2D替代SS2D来设计,从而在单个层中引入层级设计。此外,在多尺度2D扫描之后集成了一个挤压-激励(SE)块。与先前视觉Mamba架构中专注于令牌混合不同,我们的设计引入了通道混合器来增强不同通道之间的信息流动,与典型视觉Transformer的结构范式一致。我们采用由深度卷积和两个全连接层组成的ConvFFN作为通道混合器。
3. 实验结果
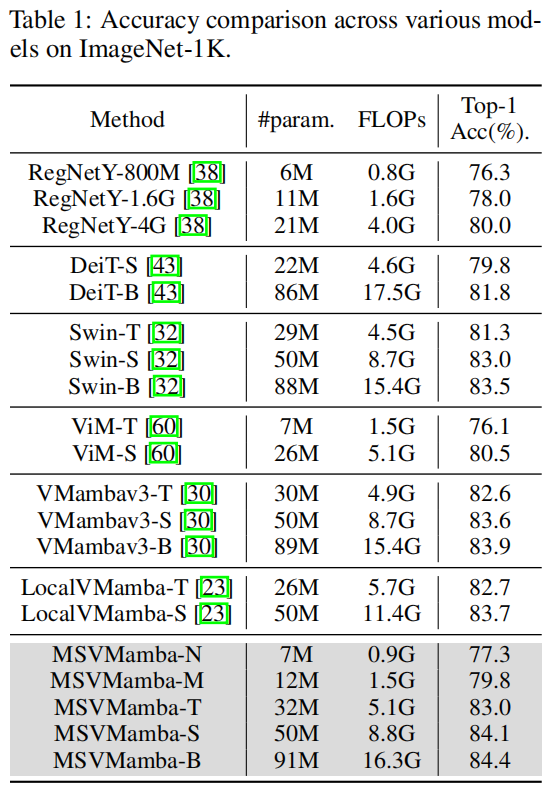
3.1 图像分类任务
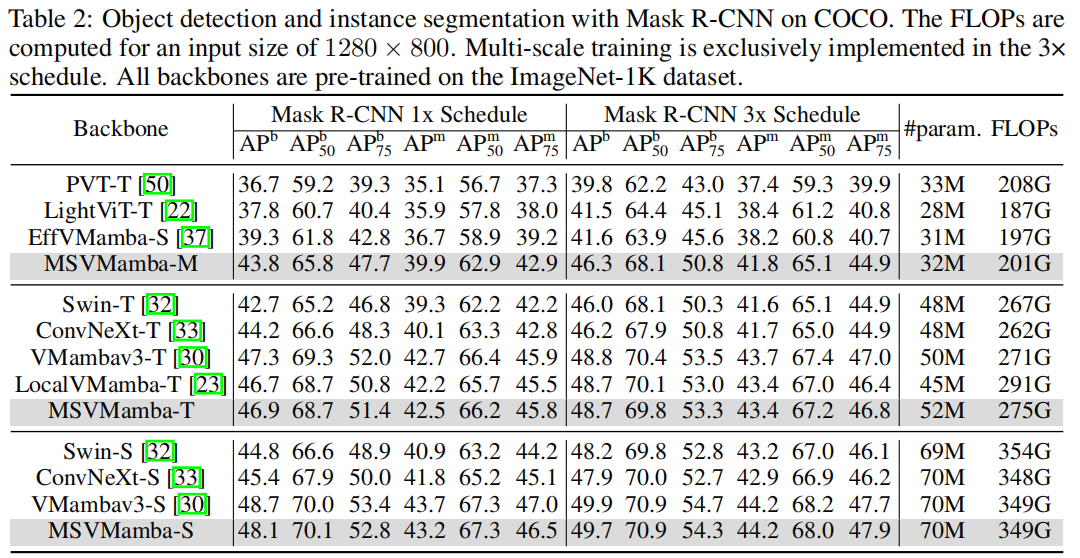
3.2 目标检测任务
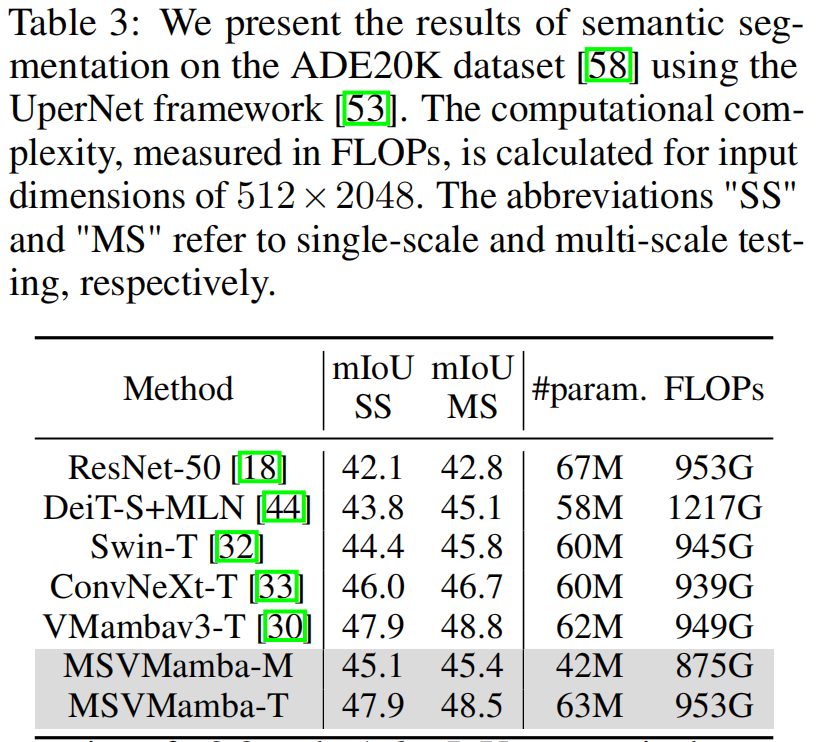
3.3 语义分割任务
3.4 消融实验
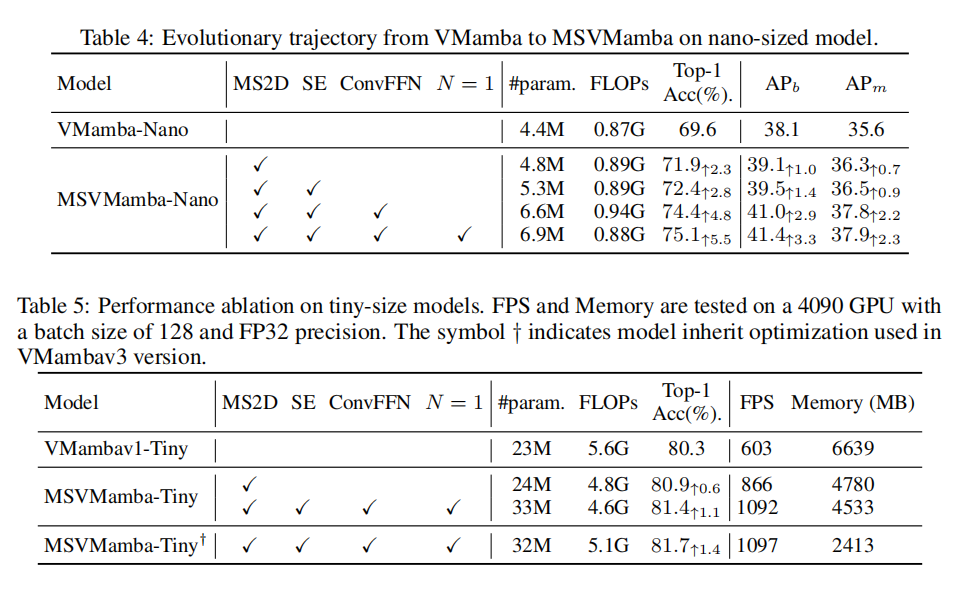
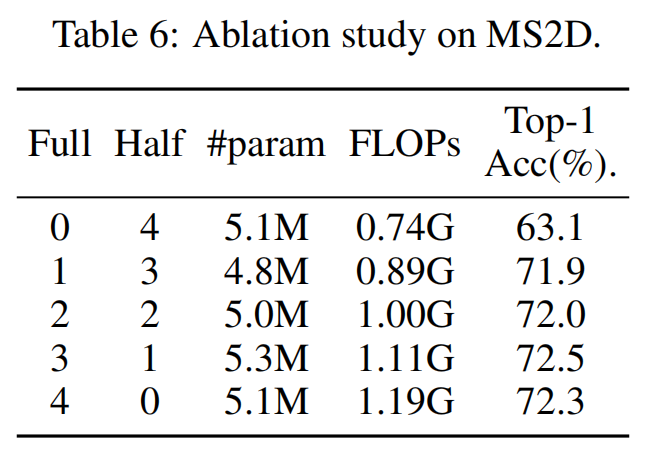
1/3 的配置以较低的计算成本(FLOPs 0.89G)实现了 71.9% 的准确率,与 3/1 的 72.5% 相比,精度差距微小但效率优势明显,因此成为最优选择。
4.局限性与结论
4.1 局限性
本文提出的多尺度VMamba(MSVMamba)旨在解决参数受限的Mamba模型在视觉任务中的“长距离遗忘问题”,尽管模型已被验证有效,但其可扩展性仍需进一步探索。这是因为长距离遗忘问题也可通过增大模型规模缓解,而当前研究未充分验证模型在更大参数规模下的性能与效率表现。
4.2 结论
本文提出了基于状态空间模型(SSMs)的视觉骨干网络Multi-Scale Vision Mamba(MSVMamba),其核心贡献与实验结果如下:
- 核心方法:通过多尺度2D(MS2D)扫描策略,在原始分辨率特征图保留细粒度特征,在下采样特征图缩短序列长度以缓解长距离遗忘问题,同时减少计算冗余;引入卷积前馈网络(ConvFFN)增强通道间信息交互,弥补SSMs通道混合能力的不足。
- 实验验证:MSVMamba在图像分类(ImageNet-1K的Tiny模型达83.0% Top-1准确率)、目标检测与实例分割(COCO数据集的1×策略下,Tiny模型box mAP达46.9%)、语义分割(ADE20K单尺度测试mIoU达47.9%)等任务中,持续优于ConvNeXt、Swin Transformer、VMamba等主流模型。
- 核心价值:MSVMamba在保持SSMs线性复杂度和全局感受野优势的同时,实现了效率与性能的更好权衡,为高效视觉骨干网络设计提供了新方案。