使用Blender可视化多传感器坐标系转换

一、背景与问题场景：为什么需要坐标转换？

在自动驾驶汽车或机器人系统中，通常会配备多种传感器，如激光雷达 (LiDAR) 和 摄像头 (Camera)。激光雷达擅长精确测量物体的距离和三维形状，而摄像头则能提供丰富的颜色和纹理信息。为了更全面地理解周围环境，我们需要将这两种不同类型的数据“融合”在一起。

核心问题：

• 物理位置不同： 激光雷达和摄像头安装在车辆的不同位置（车顶、保险杠、后视镜等），如下图所示。
• 数据坐标系不同： 每个传感器都有自己的“世界”，即坐标系。激光雷达数据点记录在“激光雷达坐标系”中，而摄像头拍摄的像素位置则基于“相机坐标系”。
• 融合的前提： 要想知道激光雷达扫描到的某个点对应摄像头图像中的哪个像素（或者反过来），我们必须知道如何将数据从一个传感器的坐标系转换到另一个传感器的坐标系。

解决方案的核心：变换矩阵

将一个点从坐标系A转换到坐标系B，需要知道坐标系B相对于坐标系A的变换矩阵。

• 变换矩阵 = 旋转矩阵 + 平移向量
  • 旋转矩阵： 描述了坐标系B相对于坐标系A是如何旋转的（比如旋转了多少度，绕哪个轴旋转）。
  • 平移向量： 描述了坐标系B的原点相对于坐标系A的原点在X, Y, Z三个方向偏移了多少距离。
• 为什么用四元数？
  • 旋转可以用多种方式表示（如欧拉角）。但欧拉角存在“万向节死锁”问题（在特定旋转角度时会丢失一个旋转自由度），导致计算不稳定。
  • 四元数 (Quaternion)： 是一种用四个数值 (w, x, y, z) 表示3D旋转的数学工具。它巧妙地避免了万向节死锁问题，计算效率高，且能平滑地表示旋转，因此在机器人学和计算机图形学中被广泛使用。你可以把它想象成一种更“聪明”的表示旋转的方式。

我们的目标： 计算出每个相机坐标系到激光雷达坐标系的变换矩阵（包含旋转四元数和平移向量）。

二、解决方案：使用Blender进行可视化转换

既然知道了需要变换矩阵，如何精确地获取它们呢？特别是如何直观地理解和验证这些数值？这里我们引入一个强大的开源工具：Blender。

为什么选择Blender？

• 专业的3D建模与可视化： Blender是一个功能强大的开源3D创作套件，可以精确地导入、编辑和可视化3D模型。
• 直观操作： 我们可以直接在3D空间中放置和调整代表传感器坐标系的物体，所见即所得。
• 精确读取数据： Blender能直接显示物体的位置（平移向量）和旋转（四元数形式），这正是我们需要的变换参数。

步骤详解：Blender可视化操作指南

步骤1：准备基础环境 - 导入车辆3D模型并设置坐标系

1. 获取精确的3D模型： 找到或创建包含车辆主体以及激光雷达和摄像头精确安装位置的3D模型文件（如.obj, .fbx, .blend格式）。
2. 导入模型到Blender： 打开Blender，通过 File -> Import 菜单导入你的车辆模型。
3. 关键设置：统一世界坐标系
   • 为了与自动驾驶/机器人领域常用的坐标系（以及后续Python代码）保持一致，我们需要将Blender的世界坐标系设置为：
     • Z轴朝上 (Up)
     • X轴朝前 (Forward - 通常是车辆前进方向/激光雷达主朝向)
     • Y轴朝左 (Left - 面向车辆前方时，你的左侧)
   • （注：Blender默认是Z轴朝上，Y轴朝前，X轴朝右。我们的设置是将Y轴前向旋转到X轴前向）
   • 如何设置： 通常需要在建模时就约定好，或在导入后整体旋转模型使其符合此约定。

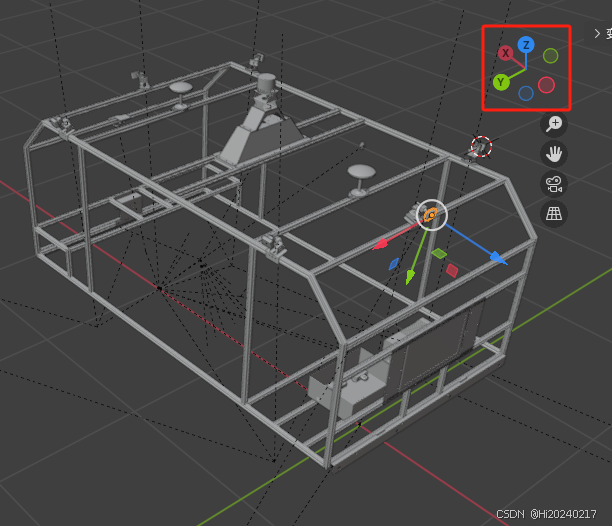
步骤2：创建代表相机坐标系的标记物

我们需要在3D空间中可视化每个相机的坐标系原点及其朝向。

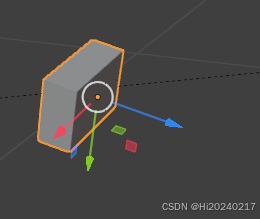
1. 创建长方体：
   • 在Blender中，按 Shift + A -> Mesh -> Cube 添加一个长方体。
   • 这个长方体将代表一个相机的坐标系原点及其三个轴的方向。
2. 调整长方体的局部坐标系：
   • 选中长方体，按 Tab 键进入编辑模式 (Edit Mode)。
   • 在视图左上角的变换方向下拉菜单中（默认可能是“全局”），选择局部坐标系 (Local Orientation)。这确保我们对长方体的旋转操作是基于它自身的轴，而不是世界轴。
   • 按 R 键进行旋转，调整长方体，使其：
     • +Z轴（蓝色轴） 指向相机的光轴方向（即相机镜头的朝向，成像的方向）。
     • （通常，+Y轴（绿色轴）指向相机图像的“向上”方向，+X轴（红色轴）指向相机图像的“向右”方向。但在本步骤中，确保Z轴指向成像方向最关键）。
3. 命名规范：
   • 在右侧的属性面板（按 N 键）的 Item 选项卡下，找到 Name 输入框。
   • 给长方体起一个清晰且符合约定的名字，例如 CAM_FRONT（前视相机）、CAM_FRONT_RIGHT（前右相机）、CAM_BACK（后视相机）等。这有助于后续识别和管理多个相机标记。

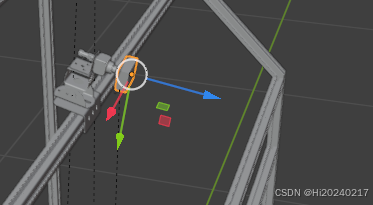
步骤3：精确对齐相机标记物到模型位置

现在需要把这个代表坐标系的长方体精确地移动到3D模型中该相机的实际安装位置。

1. 定位3D游标到相机中心：
   • 在3D视图中，将3D游标放在相机镜头中心（或已知的安装点）上。
   • 这会将Blender的3D游标（那个红白相间的圆圈图标）瞬间移动到鼠标所指模型点的精确位置。3D游标充当了一个临时参考点。
2. 将长方体吸附到游标（即相机位置）：
   • 选中代表该相机的长方体。
   • 再次按 Shift + S 打开吸附菜单。
   • 选择 Selection to Cursor。长方体中心会立即移动到3D游标所在位置，也就是相机镜头中心点。至此，长方体的位置（平移向量） 已经与相机物理位置对齐。
3. 角度微调：
   • 根据相机在车辆上的实际安装角度（可能略微俯仰或倾斜），在物体模式 (Object Mode) 下（按 Tab 键切换），按 R 键对长方体进行细微的旋转调整，确保其Z轴（蓝色）完全符合相机的实际朝向（光轴方向）。
   • 旋转时可以参考模型的细节或已知的设计图纸。

步骤4：获取激光雷达坐标系原点

激光雷达通常是整个系统的参考坐标系（“世界坐标系”），我们需要知道它的原点位置。

1. 创建长方体对齐到激光雷达：
   • 重复步骤2和步骤3。
   • 创建一个新长方体（或复制一个相机标记物修改）。
   • 将其命名为 LIDAR_TOP 或类似名称。
   • 将其精确移动并旋转到车辆3D模型上激光雷达传感器的中心位置。通常，其原点位于激光雷达旋转中心。
   • 关键： 确保这个长方体的局部坐标系方向与我们在步骤1中设定的世界坐标系方向完全一致（即+X向前，+Y向左，+Z向上）。它代表了基准坐标系。
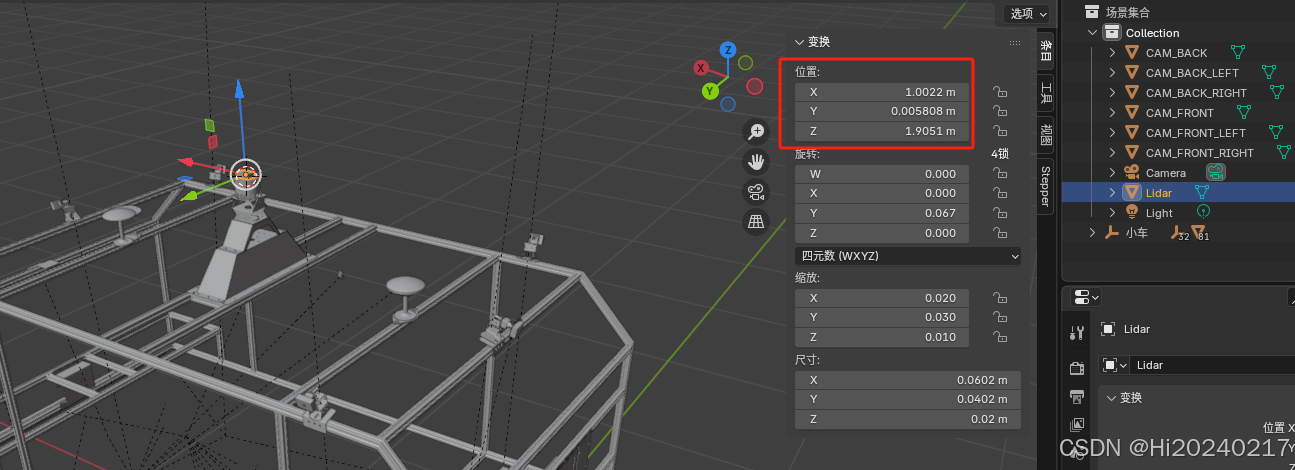
2. 记录激光雷达原点坐标：
   • 选中 LIDAR_TOP 长方体。
   • 在右侧属性面板的 Item 选项卡 -> Transform 部分，记录下 Location 的 X, Y, Z 值。这就是激光雷达坐标系原点在世界坐标系中的位置 (x_lidar, y_lidar, z_lidar)。

步骤5：获取相机到激光雷达的变换参数（四元数+平移）

现在我们可以读取每个相机相对于激光雷达坐标系的变换了。

1. 选中目标相机长方体： 在3D视图中或大纲视图 (Outliner) 中选择代表目标相机的长方体（例如 CAM_FRONT)。
2. 设置旋转显示模式为四元数：
   • 在右侧属性面板的 Item 选项卡 -> Transform 部分，找到 Rotation 旁边的模式下拉菜单（默认可能是欧拉角 Euler)。
   • 将其更改为 Quaternion (WXYZ)。现在旋转值将以四元数形式 (W, X, Y, Z) 显示。
3. 记录变换参数：
   • 平移向量 (Translation Vector)： 直接记录 Location 的 X, Y, Z 值。注意： 这个位置是相机在世界坐标系中的坐标 (x_cam_world, y_cam_world, z_cam_world)。
   • 旋转四元数 (Rotation Quaternion)： 记录 Rotation 在 Quaternion (WXYZ) 模式下显示的 W, X, Y, Z 四个数值。注意： 这个四元数表示的是相机坐标系相对于世界坐标系的旋转。
   • 相对于激光雷达： 因为我们已将激光雷达坐标系原点 (x_lidar, y_lidar, z_lidar) 和世界坐标系对齐，并且记录的是相机在世界系中的位置和旋转，那么：
     • 相机到激光雷达的平移向量 = (x_cam_world - x_lidar, y_cam_world - y_lidar, z_cam_world - z_lidar)
     • 相机到激光雷达的旋转四元数 = 相机在世界系中的旋转四元数（因为激光雷达坐标系与世界系方向一致）。如果激光雷达坐标系方向定义不同，则需要进行额外的旋转转换。

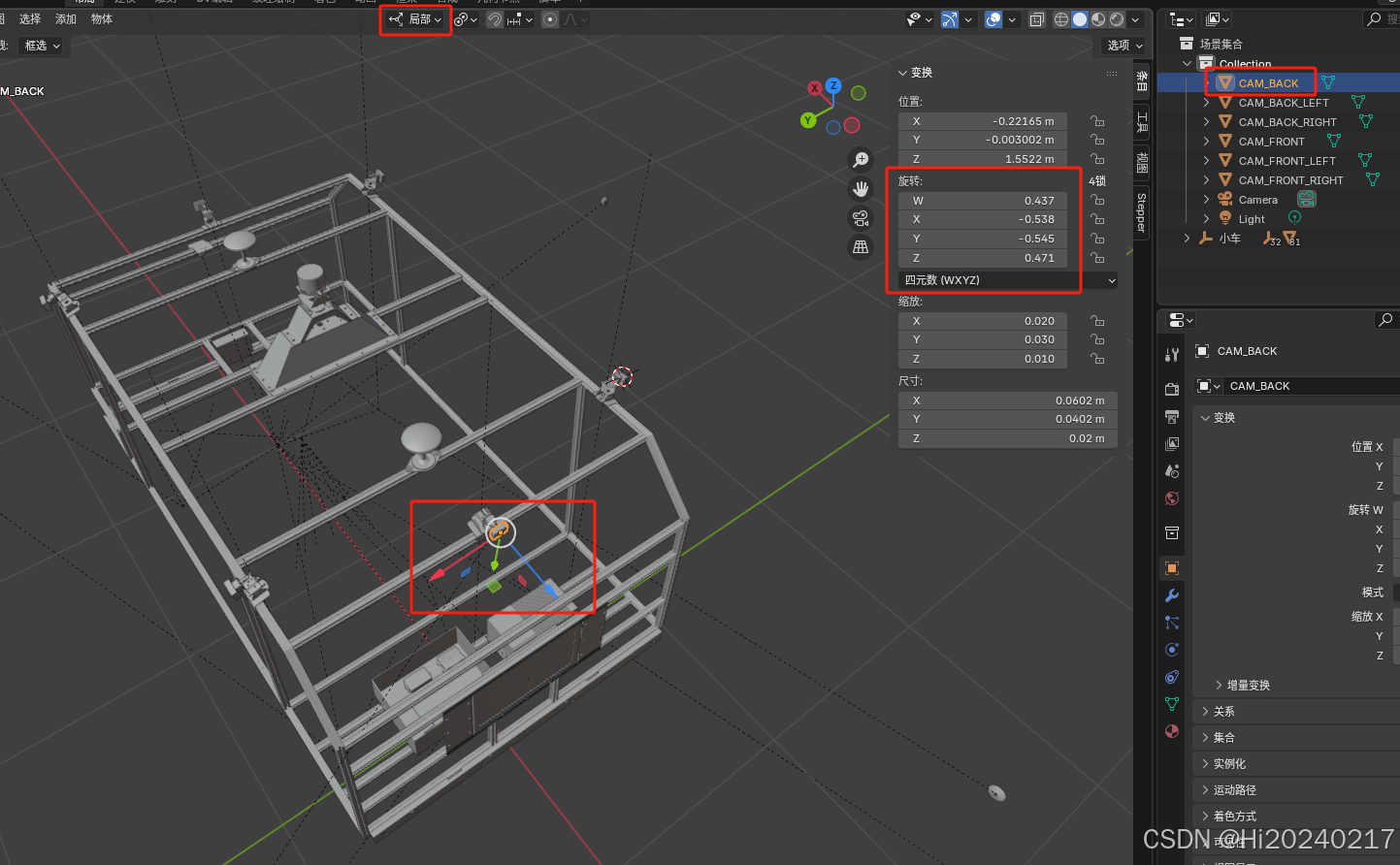
步骤6：验证变换准确性（Python可视化）

获取到参数后，我们需要验证这些变换参数是否正确。编写一个Python脚本，使用获取到的四元数和平移向量，在3D空间中重新绘制出激光雷达和各个相机的位置与朝向，并与Blender中的模型布局进行对比。

import numpy as np
import matplotlib.pyplot as plt
from pyquaternion import Quaternion
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.lines import Line2D

# 定义平移函数：将相机数据平移到以激光雷达为原点
def translate_camera_data(data, new_origin):
    """
    将相机数据平移到新的原点
    
    参数:
        data: 原始相机数据列表
        new_origin: 新的原点坐标 (x, y, z)
        
    返回:
        平移后的相机数据列表
    """
    translated_data = []
    for name, quat, pos in data:
        # 创建新的位置数组（原始位置减去新原点）
        new_pos = [pos[0] - new_origin[0], 
                   pos[1] - new_origin[1], 
                   pos[2] - new_origin[2]]
        translated_data.append([name, quat, new_pos])
    return translated_data

# 相机坐标系到世界坐标系的变换 (相机名称, 四元数(w,x,y,z), 位置(x,y,z)) 
camera_data = [
    ["CAM_FRONT       ",[0.406,-0.563,0.590,-0.413],[2.2173,-0.001318,1.5503]],
    ["CAM_FRONT_RIGHT ",[-0.002,0.021,0.795,-0.606],[1.8996,-0.83513,1.5611]],
    ["CAM_BACK_RIGHT  ",[-0.010,0.029,-0.806,0.591],[0.10054,-0.83433,1.5581]],
    ["CAM_BACK        ",[0.437,-0.538,-0.545,0.471],[-0.22165,-0.003002,1.5522]],
    ["CAM_BACK_LEFT   ",[0.591,-0.807,-0.003,-0.010],[0.10145,0.83445,1.5585]],
    ["CAM_FRONT_LEFT  ",[0.606,-0.793,0.056,-0.029],[1.9008,0.85085,1.5587]]
]

# 激光雷达坐标
new_origin = [1.0022, 0.005808, 1.9051]

# 创建平移后的相机数据
translated_camera_data = translate_camera_data(camera_data, new_origin)
print(translated_camera_data)
arrow_length = 0.2
arrow_length_ratio=0.3
    
# 创建3D图形
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')

# 原点
ax.scatter(0, 0, 0, c='r', s=100, label='Lidar Origin')
ax.quiver(0,0,0,0.5,0,0,color='red',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.quiver(0,0,0,0,0.5,0,color='lime',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.quiver(0,0,0,0,0,0.5,color='blue',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
        
# 设置坐标轴范围
ax.set_xlim([-4, 4])
ax.set_ylim([-4, 4])
ax.set_zlim([-4, 4])

# 设置坐标轴标签
ax.set_xlabel('X (Forward)')
ax.set_ylabel('Y (Left)')
ax.set_zlabel('Z (Up)')
ax.set_title("Inferring the camera's position and orientation via nuscenes v1.0-mini extrinsics")

# 处理每个相机数据（使用平移后的数据）
for name, quat_vals, pos_vals in translated_camera_data:

    # 创建四元数 (w, x, y, z)
    w,x,y,z=quat_vals
    q = Quaternion((w,x,y,z))
    R = q.rotation_matrix  # 世界坐标系到相机坐标系的旋转
    
    matrix = np.eye(4)
    matrix[:3, :3] = R           
    matrix[:3, 3] =  np.array(pos_vals) 
    

    R = matrix[:3, :3]   # 旋转矩阵
    position = matrix[:3, 3]  # 平移向量
        
    # 绘制相机位置
    ax.scatter(position[0], position[1], position[2], s=32, label=name)
    
    arrow_length = 0.3
    # 绘制相机坐标的Z轴(从原点向Z轴方向长1个单位的线)
    # 1.将Z轴一个单位向量转换到世界坐标系
    z_axis_unit_vector = np.array([0, 0, 1])
    z_axis_unit_vector_w = R@z_axis_unit_vector
    z_axis_unit_vector_w =z_axis_unit_vector_w* arrow_length
    # 2.绘制朝向箭头    
    ax.quiver(
        position[0], position[1], position[2],
        z_axis_unit_vector_w[0],
        z_axis_unit_vector_w[1],
        z_axis_unit_vector_w[2],
        color='blue',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
    ax.text(*(position+z_axis_unit_vector_w), "Z", fontsize=5)
    
    # 绘制相机坐标的Y轴(从原点向Y轴方向长1个单位的线)
    # 1.将Y轴一个单位向量转换到世界坐标系
    y_axis_unit_vector = np.array([0, 1, 0])
    y_axis_unit_vector_w = R@y_axis_unit_vector   
    y_axis_unit_vector_w = y_axis_unit_vector_w*arrow_length
    # 2.绘制朝向箭
    
    ax.quiver(
        position[0], position[1], position[2],
        y_axis_unit_vector_w[0],
        y_axis_unit_vector_w[1],
        y_axis_unit_vector_w[2],
        color='lime',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
    ax.text(*(position+y_axis_unit_vector_w), "Y", fontsize=5)
    
    # 绘制相机坐标的X轴(从原点向Y轴方向长1个单位的线)
    # 1.将X轴一个单位向量转换到世界坐标系
    x_axis_unit_vector = np.array([1, 0, 0])
    x_axis_unit_vector_w = R@x_axis_unit_vector   
    x_axis_unit_vector_w = x_axis_unit_vector_w*arrow_length
    # 2.绘制朝向箭头
    ax.quiver(
        position[0], position[1], position[2],
        x_axis_unit_vector_w[0],
        x_axis_unit_vector_w[1],
        x_axis_unit_vector_w[2],
        color='red',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
    ax.text(*(position+x_axis_unit_vector_w), "X", fontsize=5)
    
    # 添加相机名称标签
    ax.text(position[0], position[1], position[2] + 0.1, name, fontsize=5)
    
# 添加坐标轴颜色图例
axis_legend_elements = [
    Line2D([0], [0], color='red', lw=2, label='X Axis'),
    Line2D([0], [0], color='lime', lw=2, label='Y Axis'),
    Line2D([0], [0], color='blue', lw=2, label='Z Axis')
]

# 合并两个图例：相机位置图例 + 坐标轴颜色图例
handles, labels = ax.get_legend_handles_labels()
all_handles = handles + axis_legend_elements

# 添加合并后的图例
ax.legend(handles=all_handles, loc='upper left')

# 设置视角
ax.view_init(elev=25, azim=-60)

# 显示图形
plt.tight_layout()
plt.show()

代码输出 (相机在激光雷达坐标系中的位置和朝向):

相机在激光雷达坐标系中的位置和朝向:
['CAM_FRONT      ', [0.406, -0.563, 0.59, -0.413], [1.2150999999999998, -0.0071259999999999995, -0.3548]]
['CAM_FRONT_RIGHT ', [-0.002, 0.021, 0.795, -0.606], [0.8974, -0.8409380000000001, -0.3440000000000001]]
['CAM_BACK_RIGHT  ', [-0.01, 0.029, -0.806, 0.591], [-0.90166, -0.840138, -0.347]]
['CAM_BACK        ', [0.437, -0.538, -0.545, 0.471], [-1.22385, -0.00881, -0.3529]]
['CAM_BACK_LEFT   ', [0.591, -0.807, -0.003, -0.01], [-0.9007499999999999, 0.828642, -0.3466]]
['CAM_FRONT_LEFT  ', [0.606, -0.793, 0.056, -0.029], [0.8986000000000001, 0.845042, -0.34640000000000004]]

三、可视化效果：验证与解读

运行上述Python脚本后，我们将得到一幅3D图：

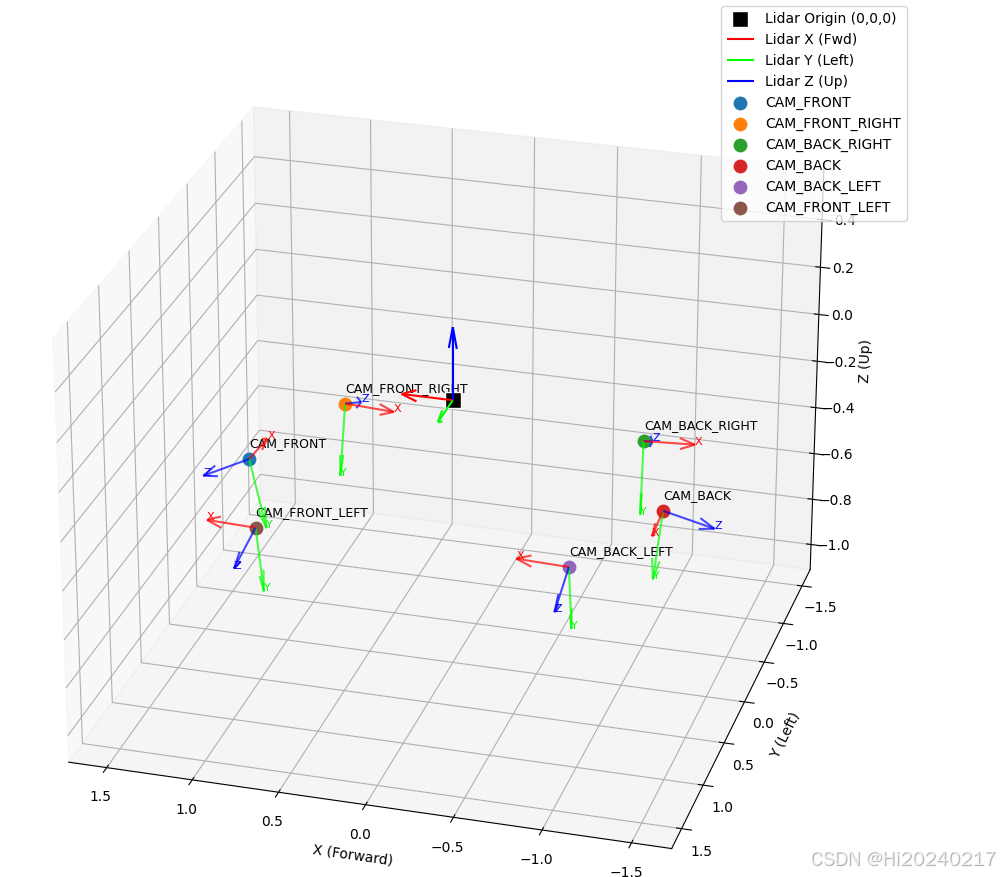
图：Python可视化结果。黑色方块代表激光雷达原点(0,0,0)，其红(X前)、绿(Y左)、蓝(Z上)轴清晰可见。彩色点代表不同相机的位置，从每个点发出的红(X)、绿(Y)、蓝(Z)箭头代表该相机自身坐标轴在激光雷达坐标系中的朝向。

如何验证结果正确？

1. 位置合理性： 观察相机点是否分布在车辆模型周围符合其安装位置的方向上（如前视相机在+X方向，后视相机在-X方向，左右相机在±Y方向）。高度(Z值)也应符合物理安装高度（通常低于激光雷达，故Z值为负）。
2. 朝向合理性：
   • 蓝色箭头 (Z轴 - 光轴)： 这是最重要的！前视相机的蓝箭头应指向车辆正前方(+X)，后视相机的蓝箭头应指向后方(-X)，侧视相机的蓝箭头应指向侧方(±Y)。
   • 绿色箭头 (Y轴 - 图像上方向)： 通常应大致指向天空(+Z方向)。
   • 红色箭头 (X轴 - 图像右方向)：
3. 对比Blender模型： 将Python可视化图与Blender中你摆放好相机和激光雷达标记物的3D视图进行对比。相机点的相对位置关系和箭头的指向趋势应该高度一致。

可视化成功意味着什么？

• 你成功地从精确的3D模型中提取出了相机到激光雷达的变换参数（旋转四元数和平移向量）。
• 这些参数是进行多传感器数据融合（如将激光雷达点投影到相机图像上，或融合激光雷达与相机检测结果）所必需的精确数学基础。
• Blender的可视化操作提供了直观、可交互的方式来理解和验证这些关键参数。

总结: 通过利用Blender强大的3D可视化能力，我们可以直观、精确地确定自动驾驶系统中不同传感器（如摄像头和激光雷达）之间的空间关系，并提取出用于数据融合的数学变换参数（四元数和平移向量）。Python可视化脚本则提供了独立的验证手段，确保提取参数的准确性。这套方法为多传感器融合系统的开发奠定了重要的基础。