神经网络的计算过程都是按照前向或者反向传播i过程来实现的,首先计算出神经网络的输出,紧接着进行一个反向传输操作,后者我们用来计算对应的梯度或者导数。
通俗来讲,神经网络的训练过程,就是经过很多次前向传播与反向传播的轮回,最终不 断调整其内部参数(权重 ω 与偏置 b),以拟合任意复杂函数的过程。前向传播指的是:从输入到输入的一个非线性函数的推理过程,获得拟合的参数,得到一个拟合参数后的激活函数。反向传播指的是:根据前向传播拟合的参数计算预测值,并计算损失函数,通过梯度下降算法不断的优化这个参数。
一、计算图
以一个简单的J函数(成本函数)为例,它的计算过程如下:
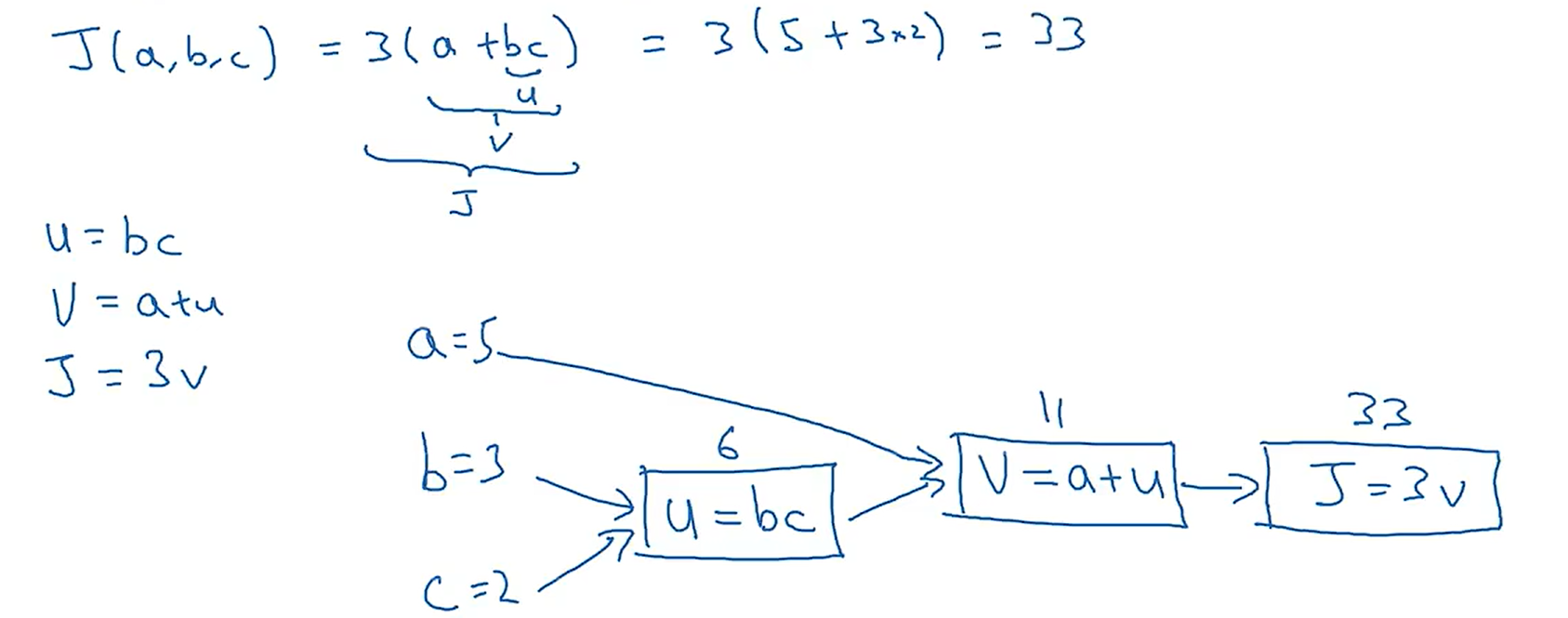
从上图可以看出,从左向右的过程,可以计算出J的值;那么从右向左的过程如下图所示:
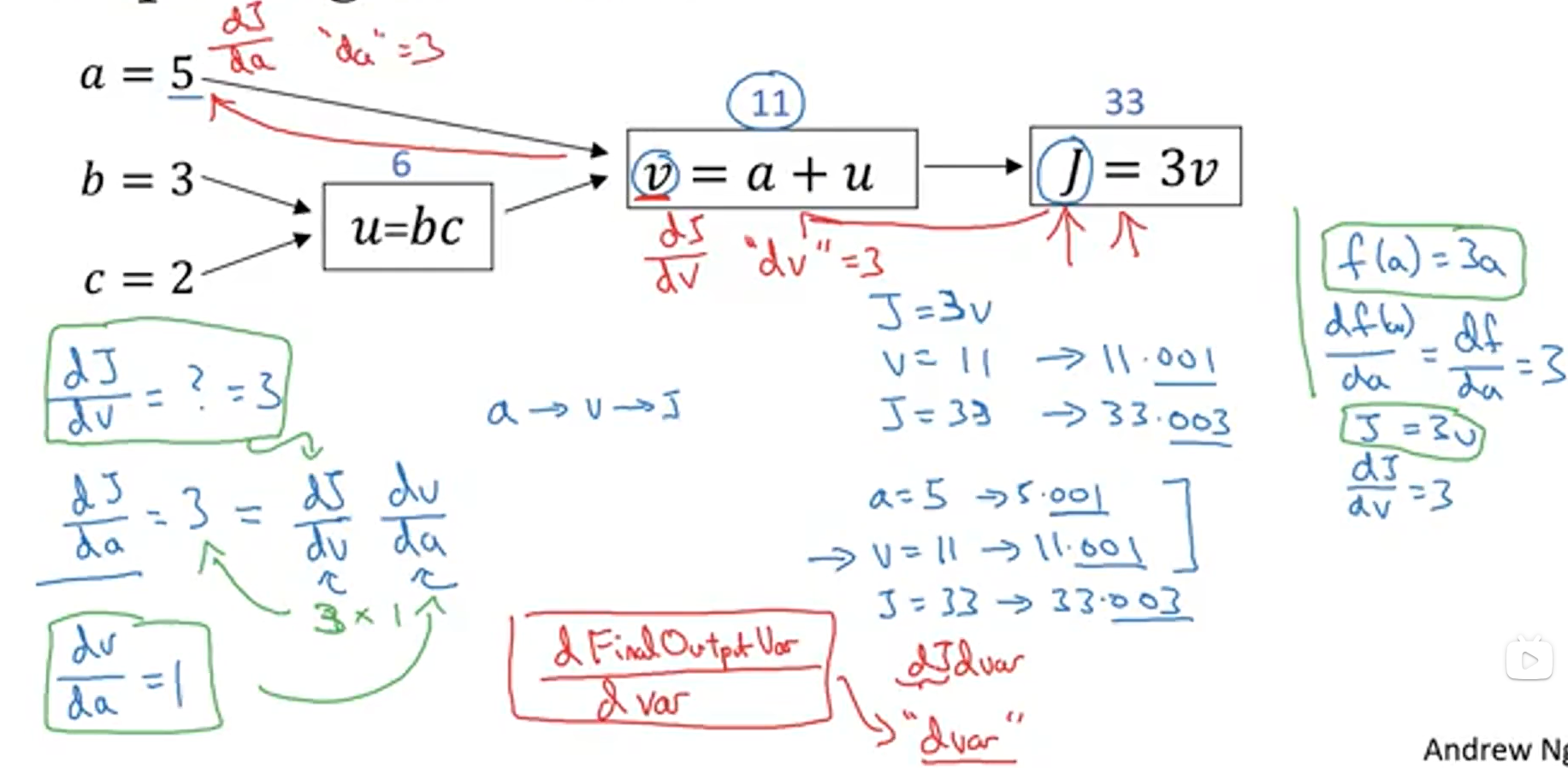
从右向左的计算过程,正对应着我们不断优化参数值,寻找最小J函数值的过程,我们知道计算一个函数的最小值,就是当这个函数的导数为0 的时候,因为我们的成本函数近似于一个凸函数,当导数为0时就对应着J函数的最小值。所以,从右向左的过程也就对应着计算导数的过程。

在从右向左的计算中,我们可以逐步计算出J函数对每一个变量的偏导数,从而便于我们对每一个变量进行梯度下降算法,找到最小的J函数值。下面是以逻辑回归的单个样本的梯度下降为实例讲解反向传播过程:
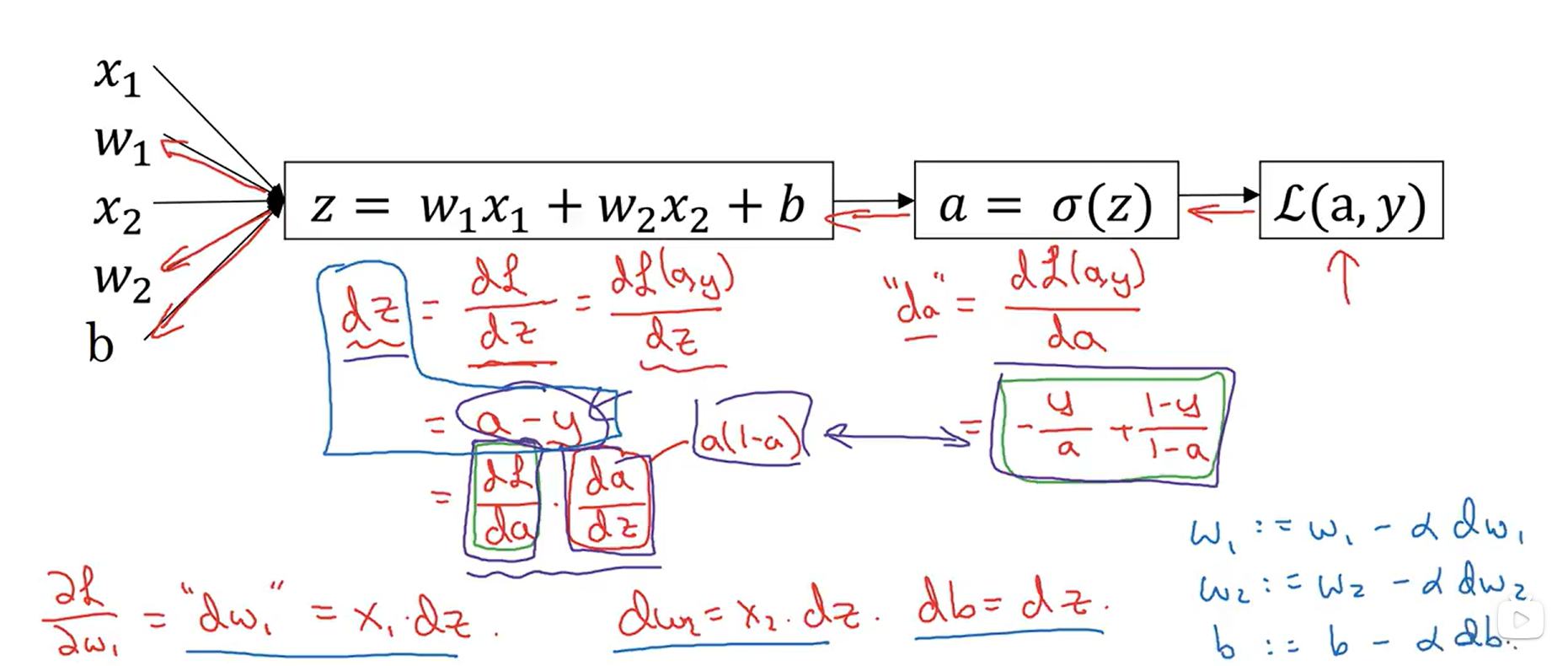
m的个样本的梯度下降,就是将所有样本关于参数的导数加起来求平均。

上述所有的示例,是为了让我们更好地理解正向传播和反向传播。
二、构建一个逻辑回归分类器来识别猫(使用神经网络思维)

(一)数据集
数据集(“data.h5”),其中包含: - 标记为 cat (y=1) 或非 cat (y=0) 的 m_train 张图像的训练集 - 标记为 cat 或非 cat 的 m_test 张图像的测试集 - 每个图像的形状(num_px、num_px、3),其中 3 表示 3 个通道 (RGB)。因此,每个图像都是正方形(高度 = num_px)和(宽度 = num_px)。训练集、测试集、每一个样本图像的像素长度或者宽度。
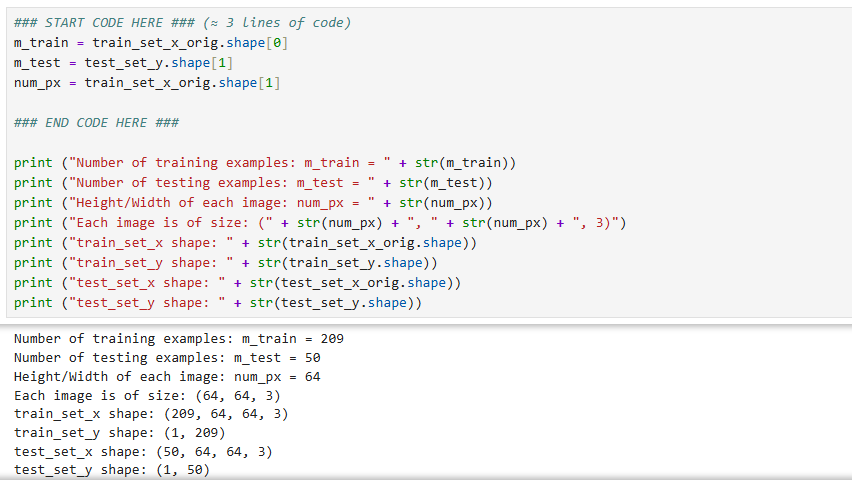
对训练集和测试集特征进行矩阵形状的重塑:在此之后,我们的训练(和测试)数据集是一个 numpy 数组,其中每列代表一个扁平化的图像。应该有 m_train 列(分别 m_test 列)。
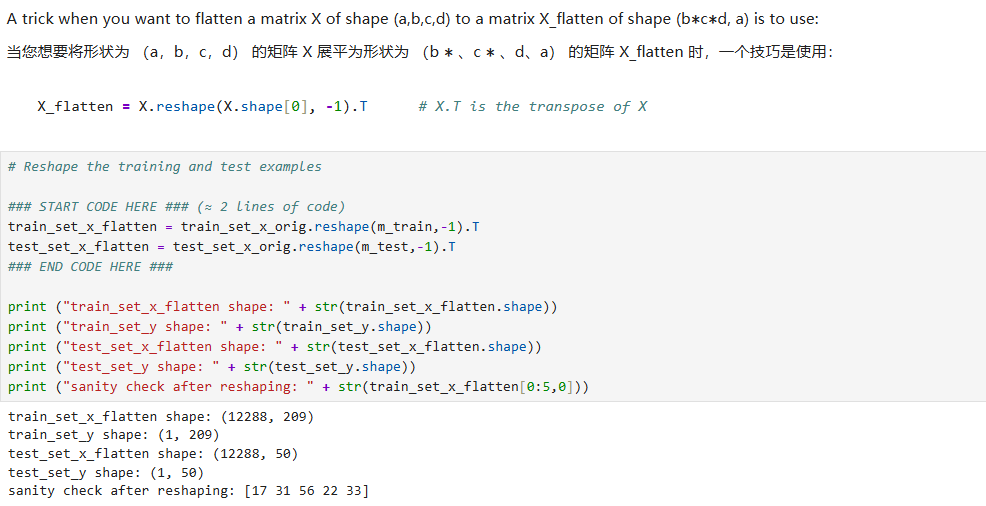
标准化数据:机器学习中一个常见的预处理步骤是将数据集居中并标准化,这意味着您从每个示例中减去整个 numpy 数组的平均值,然后将每个示例除以整个 numpy 数组的标准差。但对于图片数据集,它更简单、更方便,并且只需将数据集的每一行除以 255(像素通道的最大值)几乎一样有效。
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
(二)使用神经网络思维方式构建逻辑回归
使用逻辑回归构建识别猫的模型的基本流程如下:
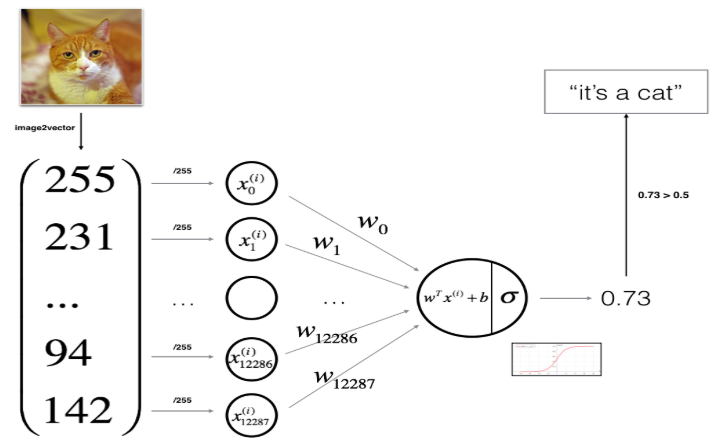
辅助函数sigmoid:
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
z -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1/(1+np.exp(-z))
### END CODE HERE ###
return s
初始化参数:
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
### START CODE HERE ### (≈ 1 line of code)
w = np.zeros((dim,1))
b = 0
### END CODE HERE ###
assert(w.shape == (dim, 1))
assert(isinstance(b, float) or isinstance(b, int))
return w, b
向前传播+向后传播:计算成本函数和梯度
# GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
Tips:
- Write your code step by step for the propagation. np.log(), np.dot()
"""
m = X.shape[1]
# FORWARD PROPAGATION (FROM X TO COST)
### START CODE HERE ### (≈ 2 lines of code)
y_pre = sigmoid(np.dot(w.T,X)+b)
cost = np.sum(Y*np.log(y_pre)+(1-Y)*np.log(1-y_pre))/(-m)
### END CODE HERE ###
# BACKWARD PROPAGATION (TO FIND GRAD)
### START CODE HERE ### (≈ 2 lines of code)
dw = np.dot(X,(y_pre-Y).T)/m
db = np.mean(y_pre-Y)
### END CODE HERE ###
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
使用梯度下降来更新参数:
# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation (≈ 1-4 lines of code)
### START CODE HERE ###
grads, cost = propagate(w, b, X, Y)
### END CODE HERE ###
# Retrieve derivatives from grads
dw = grads["dw"]
db = grads["db"]
# update rule (≈ 2 lines of code)
### START CODE HERE ###
w = w - dw*learning_rate
b = b - db*learning_rate
### END CODE HERE ###
# Record the costs
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training examples
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costs
使用优化之后的参数进行预测:
# GRADED FUNCTION: predict
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0], 1)
# Compute vector "A" predicting the probabilities of a cat being present in the picture
### START CODE HERE ### (≈ 1 line of code)
A = np.dot(w.T,X)+b
### END CODE HERE ###
for i in range(A.shape[1]):
# Convert probabilities A[0,i] to actual predictions p[0,i]
### START CODE HERE ### (≈ 4 lines of code)
if(A[0][i]<=0.5):
Y_prediction[0][i] = 0
else:
Y_prediction[0][i] = 1
### END CODE HERE ###
assert(Y_prediction.shape == (1, m))
return Y_prediction
将所有的函数合并到一个模型中:
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
### START CODE HERE ###
# initialize parameters with zeros (≈ 1 line of code)
w,b = initialize_with_zeros(X_train.shape[0])
# Gradient descent (≈ 1 line of code)
grads,cost = propagate(w, b, X_train, Y_train)
# Retrieve parameters w and b from dictionary "parameters"
params, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
w = params["w"]
b = params["b"]
# Predict test/train set examples (≈ 2 lines of code)
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
### END CODE HERE ###
# Print train/test Errors
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
总结;1.预处理数据集很重要。2. 分别实现了每个函数:initialize()、propagate()、optimize()。然后构建了一个 model()。3. 调整学习率(这是“超参数”的一个例子)可以对算法产生很大的影响。
最后,防止过拟合可以加入正则化项,学习率的选择可以使用动态优化学习率函数。机器学习课程中都有讲过。