目录
1)前序遍历(Preorder Traversal 亦称先序遍历):
链式结构二叉树
用链表来表示⼀棵⼆叉树,即用链来表示元素的逻辑关系。 通常的⽅法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址
创建一个链式二叉树
BTNode* buynode(char x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
node->data = x;
node->left = node->right = NULL;
return node;
}
BTNode* createBinarytree()
{
BTNode* nodeA = buynode('A');
BTNode* nodeB = buynode('B');
BTNode* nodeC = buynode('C');
BTNode* nodeD = buynode('D');
BTNode* nodeE = buynode('E');
BTNode* nodeF = buynode('F');
nodeA->left = nodeB;
nodeA->right = nodeC;
nodeB->left = nodeD;
nodeC->left = nodeE;
nodeC->right = nodeF;
return nodeA;
}
二叉树操作:
#pragma once
#include<stdio.h>
#include<stdlib.h>
//定义链式结构二叉树
typedef char BTDataType;
typedef struct BinarytreeNode
{
BTDataType data;
struct BinarytreeNode* left;
struct BinarytreeNode* right;
}BTNode;
//前序遍历——根左右
void preOrder(BTNode* root);
//中序遍历
void inOrder(BTNode* root);
//后序遍历
void postOrder(BTNode* root);
// ⼆叉树结点个数
int BinaryTreeSize(BTNode* root);
//int BinaryTreeSize(BTNode* root,int* psize);
// ⼆叉树叶⼦结点个数
int BinaryTreeLeafSize(BTNode* root);
// ⼆叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
//⼆叉树的深度/⾼度
int BinaryTreeDepth(BTNode* root);
// ⼆叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// ⼆叉树销毁
void BinaryTreeDestory(BTNode** root);
//层序遍历
void leverOrder(BTNode* root);二叉树的遍历
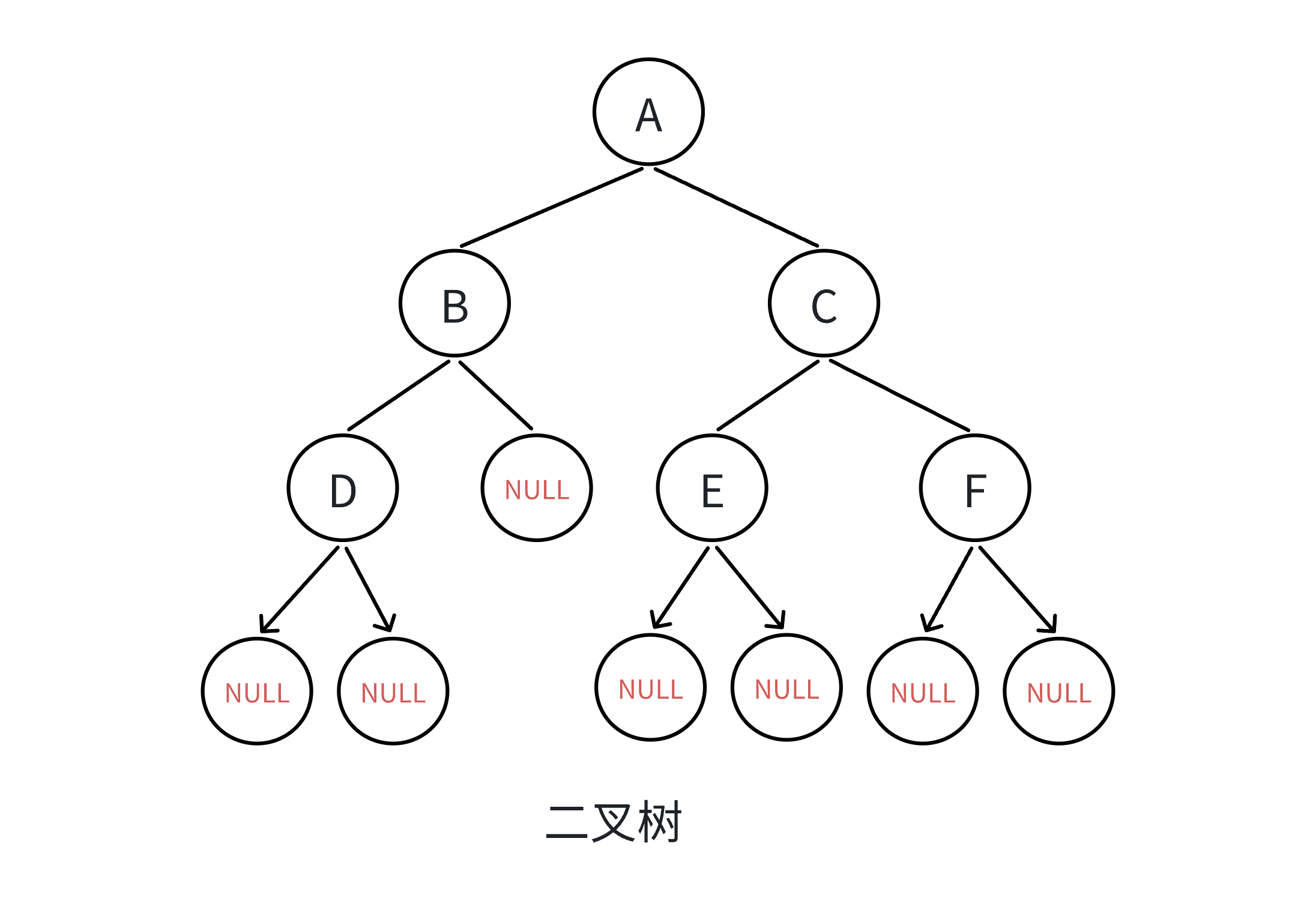
规则:
1)前序遍历(Preorder Traversal 亦称先序遍历):
访问根结点的操作发⽣在遍历其左右⼦树之前
访问顺序为:根结点、左⼦树、右⼦树
代码实现:
//前序遍历--根左右
void preOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->data);
preOrder(root->left);
preOrder(root->right);
}
基本思路
如果当前节点为空,输出 "NULL" 并返回
否则先访问当前节点(输出节点数据)
然后递归遍历左子树
最后递归遍历右子树
2)中序遍历(Inorder Traversal):
访问根结点的操作发⽣在遍历其左右⼦树之中(间)
访问顺序为:左⼦树、根结点、右⼦树
代码实现:
//中序遍历--左根右
void inOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
inOrder(root->left);
printf("%c ", root->data);
inOrder(root->right);
}
基本思路:
- 如果当前节点为空,输出 "NULL" 并返回
- 首先递归遍历左子树
- 然后访问当前节点(输出节点数据)
- 最后递归遍历右子树
可用于二叉树的排序操作和某些特定问题的求解(如寻找前驱 / 后继节点)
3)后序遍历(Postorder Traversal):
访问根结点的操作发⽣在遍历其左右⼦树之后
访问顺序为:左⼦树、右⼦树、根结点
代码实现:
//后序遍历
void postOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
postOrder(root->left);
postOrder(root->right);
printf("%c ", root->data);
}
基本思路:
- 若当前节点为空,输出 "NULL" 并返回
- 首先递归遍历左子树
- 然后递归遍历右子树
- 最后访问当前节点(输出节点数据)
应用场景:
- 释放二叉树的内存(需先释放子节点,再释放根节点)
- 计算二叉树的高度
- 某些表达式树的求值等场景
求结点个数
方法1:
代码实现:
//⼆叉树结点个数
int size = 0;
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
//结点非空,+1
size++;
BinaryTreeSize(root->left);
BinaryTreeSize(root->right);
return size;
}
缺点:
全局变量的副作用:
使用全局变量size记录节点数量,会导致多次调用函数时结果不正确。例如第一次调用后size已累加了所有节点,第二次调用会在原有基础上继续增加,而不是重新计算。递归逻辑的冗余:
函数虽然进行了递归调用,但并没有利用递归的返回值,而是单纯依赖全局变量计数。
方法2:
代码实现:
// ⼆叉树结点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
- 不需要全局变量,每次调用都是独立计算
- 逻辑更清晰,直接体现了 "节点总数 = 1(当前节点)+ 左子树节点数 + 右子树节点数" 的递归关系
- 无副作用,可多次调用且结果正确
求叶子结点个数
代码实现:
// ⼆叉树叶⼦结点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left)
+ BinaryTreeLeafSize(root->right);
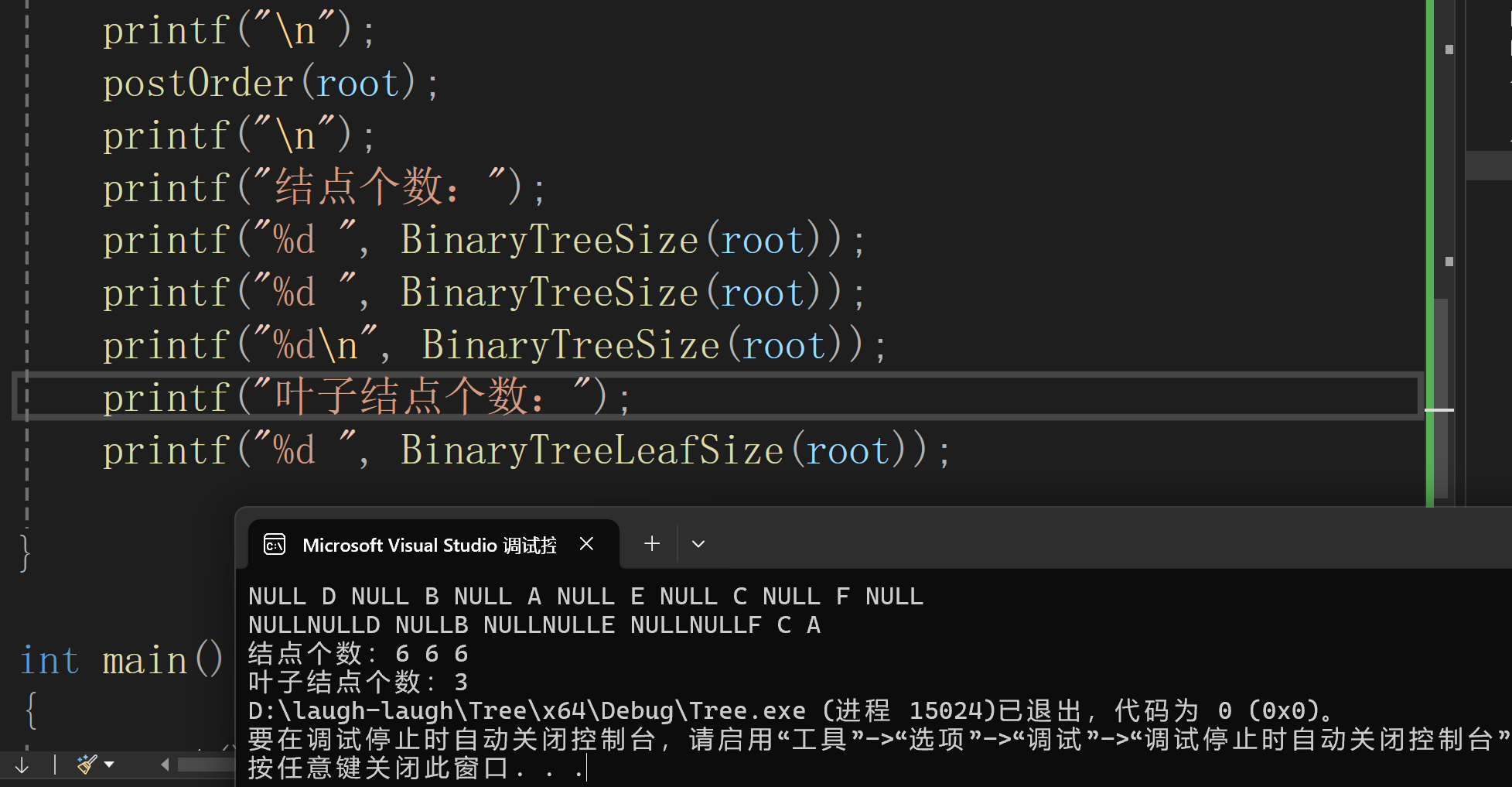
}基本思路:
函数采用递归思路,核心逻辑是:
- 如果当前节点为空,返回 0(空节点不是叶子节点)
- 如果当前节点的左右子树都为空,说明这是叶子节点,返回 1
- 否则,当前节点不是叶子节点,递归计算左子树和右子树的叶子节点数并求和
优势:
- 没有使用全局变量,每次调用都是独立计算,无副作用
- 递归终止条件明确,逻辑严谨
- 代码简洁,直接体现了叶子节点的定义(左右子树均为空)
二叉树第k层节点数
代码实现:
// ⼆叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (k <= 0)
{
return 0; // 无效层数返回0
}
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}核心思想:
函数的递归逻辑:
- 如果当前节点为空,返回 0(空树没有任何节点)
- 如果 k 等于 1,说明当前就是要统计的层,返回 1(当前节点本身)
- 否则,递归计算左子树的第 k-1 层和右子树的第 k-1 层节点数之和
核心思想:
利用了 "父节点的第 k 层 = 子节点的第 k-1 层" 这一特性,通过递归将问题逐步简化,直到简化到第 1 层(当前节点)
优点:
- 无需全局变量,每次调用独立计算
- 递归逻辑清晰,符合二叉树的层次特性
- 时间复杂度为 O (n),n 为树的节点总数,效率较高
二叉树深度和高度
代码实现:
//⼆叉树的深度 / ⾼度
int BinaryTreeDepth(BTNode * root)
{
if (root == NULL)
{
return 0;
}
int leftDep = BinaryTreeDepth(root->left);
int rightDep = BinaryTreeDepth(root->right);
return 1 + (leftDep > rightDep ? leftDep : rightDep);
}基本思路:
函数的递归思路:
- 如果当前节点为空,返回 0(空树的深度为 0)
- 否则,递归计算左子树的深度(leftDep)和右子树的深度(rightDep)
- 当前树的深度 = 1(当前节点本身) + 左右子树中较深的那个一个的深度
核心逻辑:
二叉树的深度定义为从根节点到最远叶子节点的最长路径上的节点数
优点:
- 递归逻辑自然,符合二叉树深度的数学定义
- 时间复杂度为 O (n),每个节点只需访问一次
- 空间复杂度为 O (h),h 为树的深度,由递归栈的深度决定
二叉树查找数据
代码实现:
// ⼆叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* leftFind = BinaryTreeFind(root->left, x);
if (leftFind)
{
return leftFind;
}
BTNode* rightFind = BinaryTreeFind(root->right, x);
if (rightFind)
{
return rightFind;
}
return NULL;
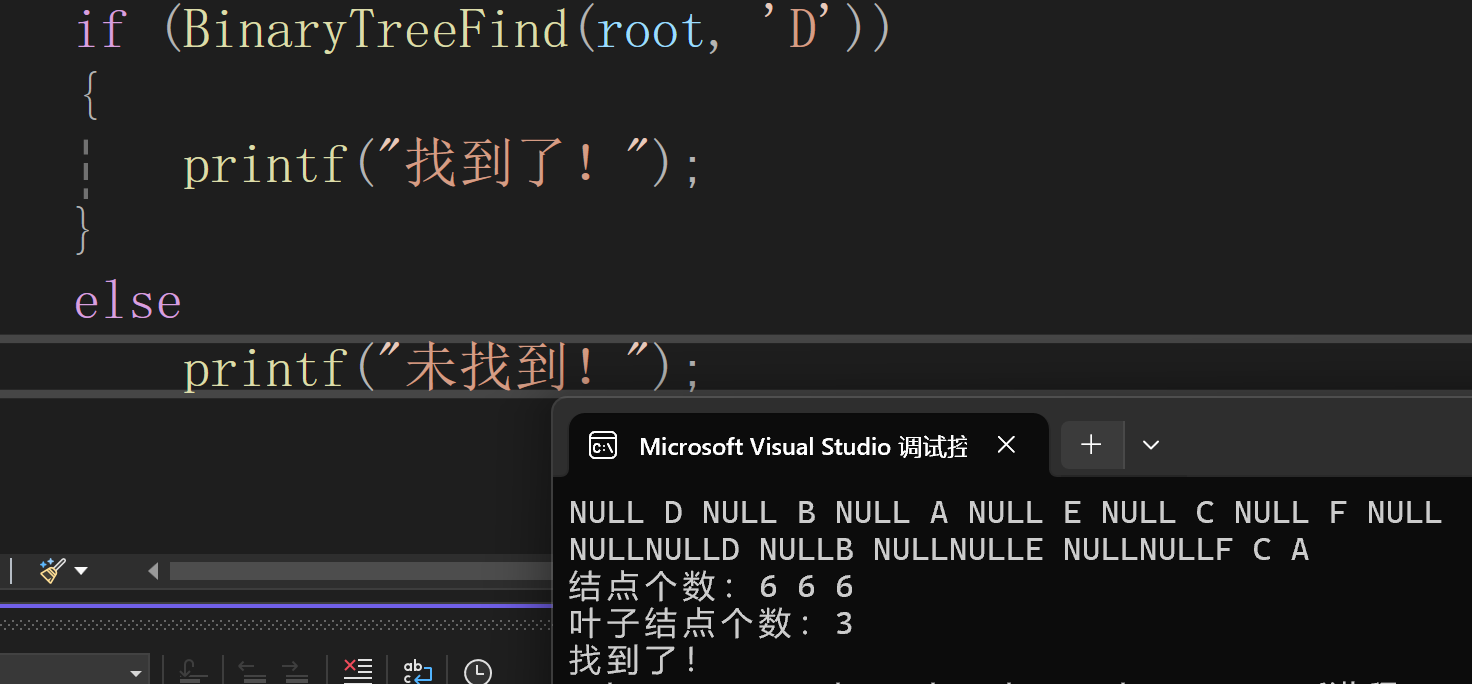
}基本逻辑:
- 如果当前节点为空,返回
NULL(未找到) - 如果当前节点的值等于
x,返回当前节点(找到目标) - 否则,先递归在左子树中查找:
- 若左子树中找到(
leftFind不为空),直接返回找到的节点 - 若左子树中未找到,再递归在右子树中查找
- 右子树中找到则返回,否则返回
NULL
- 若左子树中找到(
注意事项:
如果树中存在多个值为
x的节点,该函数只会返回第一个遇到的节点(按前序遍历顺序)时间复杂度为 O (n),在最坏情况下需要遍历所有节点
二叉树销毁
代码实现:
// ⼆叉树销毁--左右根
void BinaryTreeDestory(BTNode** root)
{
if (*root == NULL)
{
return;
}
BinaryTreeDestory(&((*root)->left));
BinaryTreeDestory(&((*root)->right));
free(*root);
*root = NULL;
}逻辑
- 采用二级指针作为参数,因为需要修改指针本身的值(将其置空)
- 如果当前节点为空(*root == NULL),直接返回
- 先递归销毁左子树(左右根中的 "左")
- 再递归销毁右子树(左右根中的 "右")
- 最后释放当前节点的内存,并将指针置空(左右根中的 "根")
后序遍历
必须先确保子节点都已被释放,避免出现悬挂指针,释放当前节点前需要访问其左右子节点指针,不能提前释放
当我们释放节点内存后,需要将原指针设置为 NULL 以避免野指针。由于 C 语言是值传递,要修改指针本身的值,必须传递指针的地址(即二级指针)。
层序遍历
代码实现
//层序遍历
void leverOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
//取队头,出队头
BTNode* top = QueueFront(&q);
QueuePop(&q);
printf("%c ", top->data);
//将队头非空左右孩子入队列
if (top->left)
QueuePush(&q, top->left);
if (top->right)
QueuePush(&q, top->right);
}
QueueDestroy(&q);
}思路:
- 利用队列的先进先出(FIFO)特性,实现从根节点开始,按层次依次访问所有节点
- 先将根节点入队,然后循环执行:出队一个节点并访问,再将其左右子节点入队
- 直到队列为空,说明所有节点都已访问完毕
特点:
- 使用队列作为辅助数据结构,是层序遍历的标准实现方式
- 遍历顺序与树的层次一致,符合 "广度优先" 的特性
- 时间复杂度为 O (n),每个节点入队和出队各一次
- 空间复杂度为 O (n),最坏情况下(满二叉树)队列需要存储 n/2 个节点
若如果根节点为 NULL,需要在函数开头增加判断,避免对空指针操作。