目录
前言
在软件的世界里,程序 = 数据结构 + 算法。这句广为流传的名言,深刻地揭示了数据结构的核心地位。它是我们组织、存储和管理数据的艺术,是构建高效、稳定应用程序的基石。而在众多数据结构中,线性表作为最基础、最常用的一种,其重要性不言而喻。
顺序表和单向链表,正是线性表两种最经典的实现方式。它们如同“一体两面”,代表了计算机中两种最根本的物理存储思想:连续的空间与离散的空间。
顺序表凭借其底层连续的物理结构,带来了无与伦比的随机访问性能,仿佛一本页码清晰的书籍,我们可以根据目录瞬间翻到任何一页。然而,这种连续性的代价便是在中间进行插入或删除时,可能引发大规模的“数据搬迁”,效率堪忧。
单向链表则巧妙地利用指针,将离散的内存空间“串联”起来。它牺牲了随机访问的能力,换来了在任意位置高效插入与删除的灵活性,如同一条环环相扣的链条,只需改变节点的指向,即可轻松完成结构的调整。
理解二者的内在原理、优缺点以及适用场景,是每一位开发者内功修炼的必经之路。这不仅是为了应对面试官的考问,更是为了在未来的开发中,能够根据实际需求,做出最合理的技术选型,写出性能更优、更优雅的代码。
一、数据结构和算法说明
1、基本概念
说明:
数据结构是一门研究如何有效组织数据,并提高数据处理效率的学科,通过研究各种数据内部的逻辑关系,使用某种特定的存储形式,并在此基础上对数据实施各种操作,这些工作被称为广义上的算法。
(1)逻辑关系
逻辑关系指数据元素之间的内在关联方式
常见的逻辑结构包括:集合、线性表(线性关系)、树、图(非线性关系)
逻辑结构是数据元素之间固有的属性,与数据处理方式无关
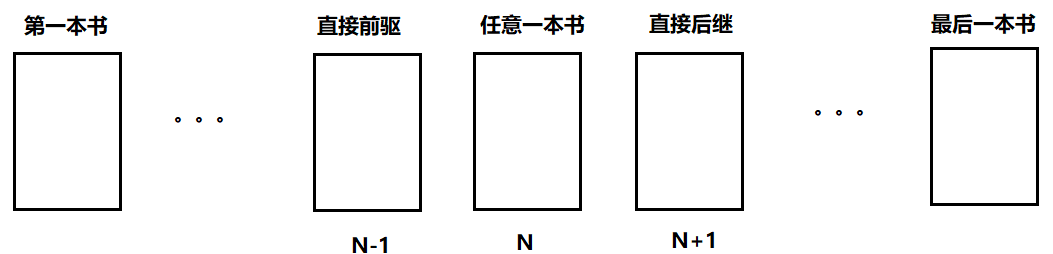
a、线性关系
说明:元素间存在一对一的前驱后继关系
特点:除首尾元素外,每个元素有且仅有一个直接前驱和一个直接后继
示例:图书馆中按编号排列的书籍(编号N的前驱是N-1,后继是N+1)
图解:
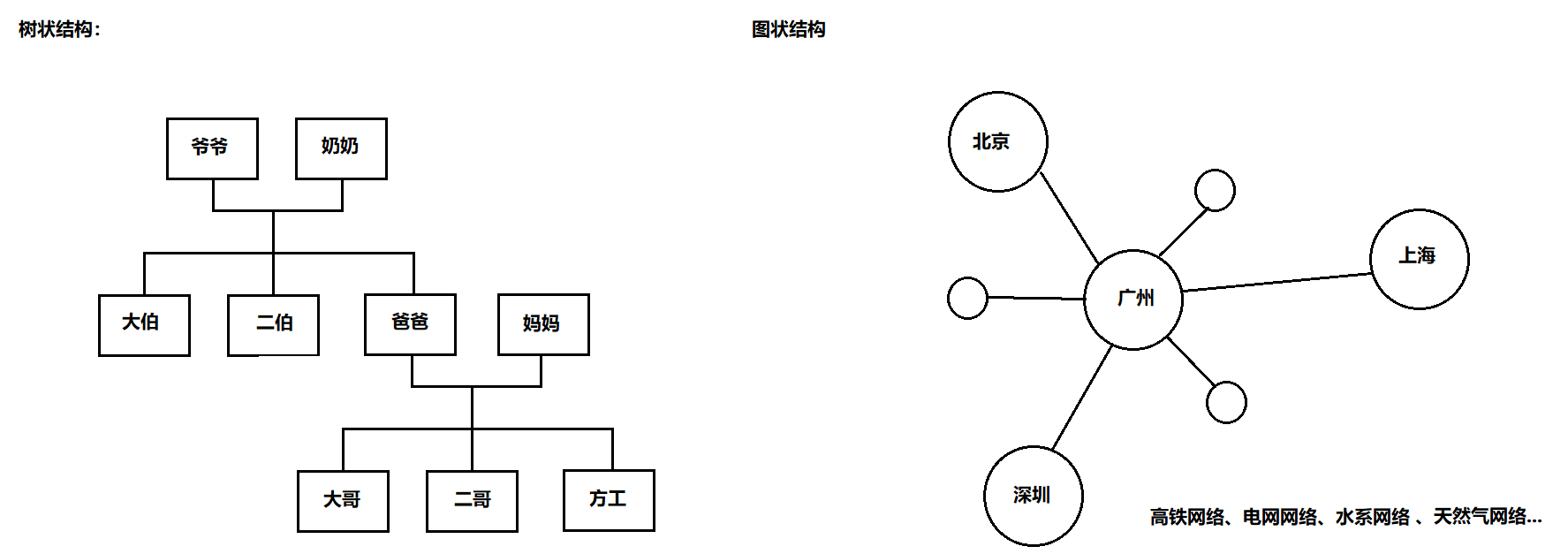
b、非线性关系
说明:元素间不是严格的一对一关系
特点:一个元素可能与多个其他元素相关联
示例:家族族谱(一个人有双亲和多子女)、交通网络(城市间多条道路连接)
图解:
(2)存储说明
a、基本说明
存储形式指数据在计算机内存中的具体表示方式
常见存储方式:顺序存储、链式存储等
不同的存储方式对数据处理效率有显著影响
重要提示:逻辑结构与存储形式之间没有必然联系,同一逻辑结构可采用不同存储方式实现
b、存储方式对比
顺序存储:数据元素存储在连续的存储单元中
链式存储:通过指针连接分散的存储单元,每个节点包含数据和指针
c、存储选择原则
根据具体应用场景的需求,在空间效率和时间效率之间寻求最佳平衡
2、算法性能分析
(1)概念:
算法分析是在确保算法正确性的前提下,对其优劣进行评估的过程。优秀的算法通常具备以下特征:
时间效率高:程序执行时间短
空间效率高:程序占用内存空间少
结构良好:代码易读、易移植、易调试
本质:提高程序的时空效率,即在保证功能正确的基础上,追求更快的执行速度和更少的内存占用。虽然时空特性往往相互制约,但可根据实际需求进行平衡和取舍。
(2)时间复杂度:
说明:
时间复杂度不考察代码运行的绝对时间(受硬件影响),而是分析语句执行总次数(语句频度)。
例:
// 普通函数 void counting(int n) { for (int i = 1; i <= n; i++) { printf("本语句将会出现%d次\n", i); // n也就是100次(时间复杂度:n) for (int j = 1; j <= n; j++) { printf("本语句将会出现%d次\n", j); // n*n 也就是100*100次(时间复杂度:n*n) } } } // 结论:只需要关心多项式的最高次幂(比如:n*n + n, 只需要考虑n*n即可,后面的+n对时间复杂度影响有限,可以忽略)说明:
计算原则
总运算次数:T(n) = n² + n
时间复杂度:O(n²)(只保留最高次幂,低次项和系数可忽略)
常见时间复杂度表示
T(n):总运算次数函数
O(n):时间复杂度表示法(大O表示法)
对数运算:log₂4 = 2(表示2的2次方等于4)
平方根:√4 = 2,√16 = 4
阶乘:n! = n × (n-1) × ... × 1
(3)空间复杂度
空间复杂度衡量算法运行过程中所需的内存空间大小,通常用字节数表示。分析重点包括:
变量存储空间
数据结构占用空间
递归调用栈空间等
(4)时空复杂度权衡
时空效率往往存在相互制约的关系:
时间优化:可能通过增加缓存、预处理数据等方式,消耗更多内存
空间优化:可能通过压缩存储、延迟计算等方式,增加计算时间
实践原则:根据具体应用场景的需求侧重,合理权衡时空效率:
实时系统:优先考虑时间效率
嵌入式设备:优先考虑空间效率
一般应用:在时空之间寻求最佳平衡点
二、顺序表
1、基本概念
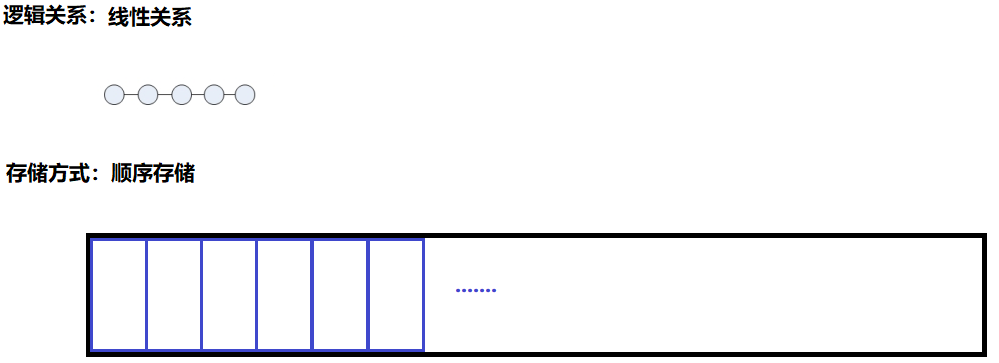
说明:
顺序存储的线性表(线性关系+顺序存储)
图解:
说明:
就是将数据存储到一片连续的内存中,在C语言的环境下,可以是具名的栈数组,或者是匿名的堆数组(因为可存储的空间大),存储方式不仅仅只是提供数据的存储空间,而是必须要能体现数据之间的逻辑关系,当采用顺序存储的方式来存放数据 时,唯一能够用来表达数据间本身的逻辑关系就是存储位置.
2、顺序表的设计
1、顺序表的管理结构体设计 2、初始化顺序表 3、增删查改顺序表 // 前提:判断顺序表是否满了或者空了 a、删:销毁顺序表、将顺序表指定位置的数据删除 b、增:向顺序表中的表头插入一个数据 c、查:遍历顺序表 d、改:根据位置修改顺序表中的数据(1)管理结构体设计
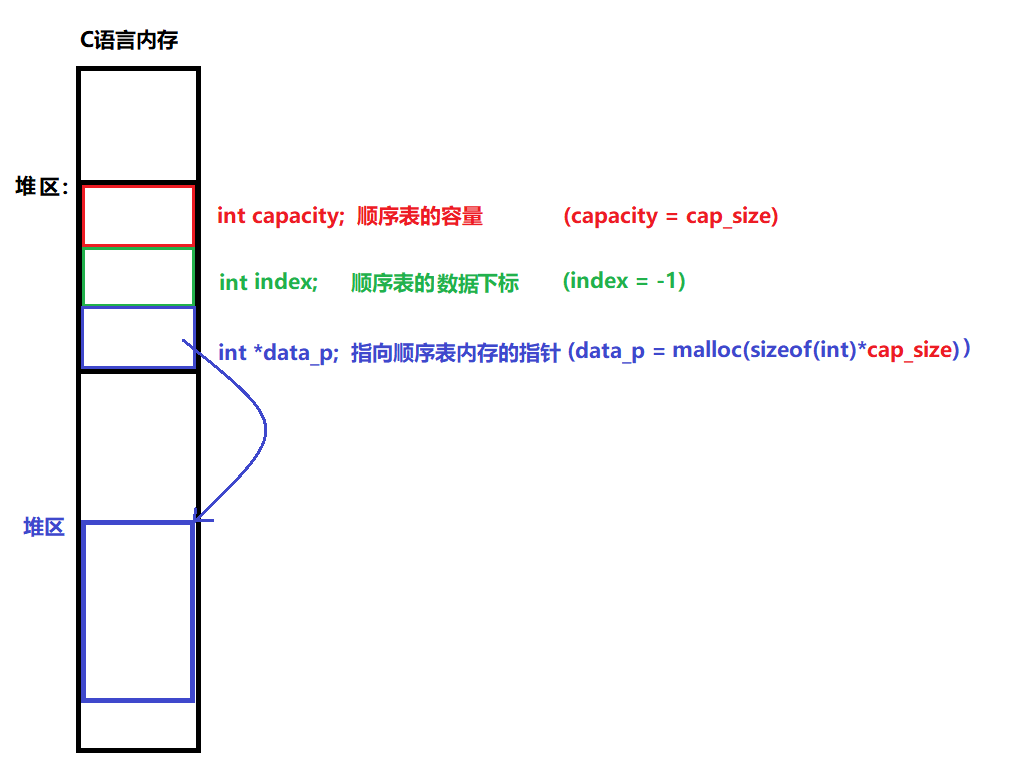
说明:
顺序表的总容量
顺序表的当前最末数据的下标位置
指向顺序表内存(堆内存)的指针
图解:
示例代码;
typedef struct sq_list { int capacity; // 顺序表的容量 int index; // 顺序表的数据下标(最末尾数据的下标) int *data_p; // 指向顺序表内存的指针 }sq_list_t, *sq_list_p;(2)初始化顺序表
说明:
所谓初始化就是建立一个不包含任何元素的顺序表,设置好管理结构体中的表的总容量、末数据小标、申请好顺序表内存空间等系列准备工作
图解:
示例代码:
/** * @brief 初始化顺序表 * @note None * @param cap_size:顺序表的容量 * @retval 成功:返回顺序表的管理结构体的指针 * 失败:返回NULL */ sq_list_p SEQUENTIAL_LIST_Init(unsigned int cap_size) { // 1、给顺序表管理结构体申请一个堆内存空间 sq_list_p p = malloc(sizeof(sq_list_t)); bzero(p, sizeof(sq_list_t)); // 2、给申请的空间进行赋值操作 if ( p!= NULL) { p->capacity = cap_size; // 顺序表的内存空间的容量(有多少个数据) p->index = -1; // 顺序表的数据下标(最末尾数据的下标) --- 一开始没有数据存入,所以是-1(0的话是第一个数据) p->data_p = malloc(sizeof(int)*cap_size); // 指向顺序表内存的指针(申请一个堆空间,并让指针指向它) if (p->data_p == NULL) // 判断p->data_p是否申请堆空间失败,如果失败,就将管理结构体空间释放并返回NULL { free(p); return NULL; } } else // 判断p是否申请堆空间失败,如果失败,就返回NULL { return NULL; } // 3、返回管理结构体的指针 return p; }(3)销毁顺序表
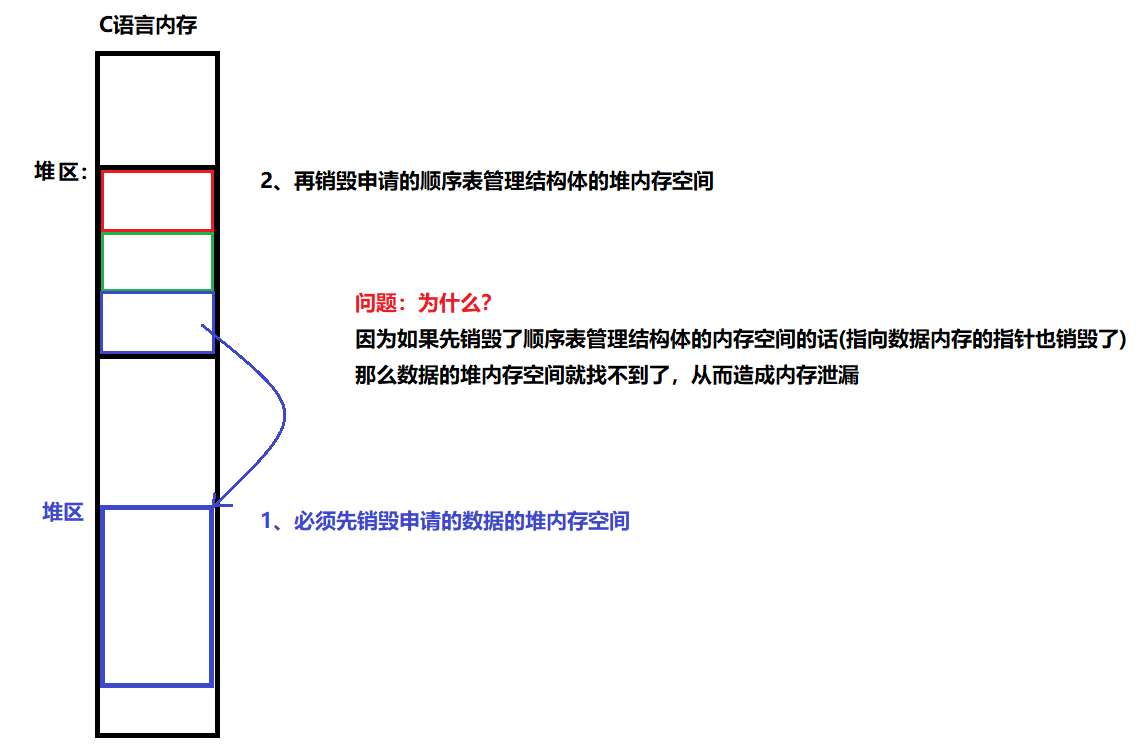
说明:
一个顺序表后面如果不再使用,应当要释放其所占用的内存空间,这被称为顺序表的销毁
图解:
代码:
/** * @brief 销毁顺序表 * @note None * @param p:顺序表管理结构体的指针(我们通过它来将整个顺序表全部销毁) * @retval None */ void SEQUENTIAL_LIST_UnInit(sq_list_p p) { // 1、如果顺序表本身就为NULL,就不必继续下面的内容了 if (p == NULL) return; // 2、释放堆内存空间(由内到外) free(p->data_p); free(p); }(4)判断是否为空
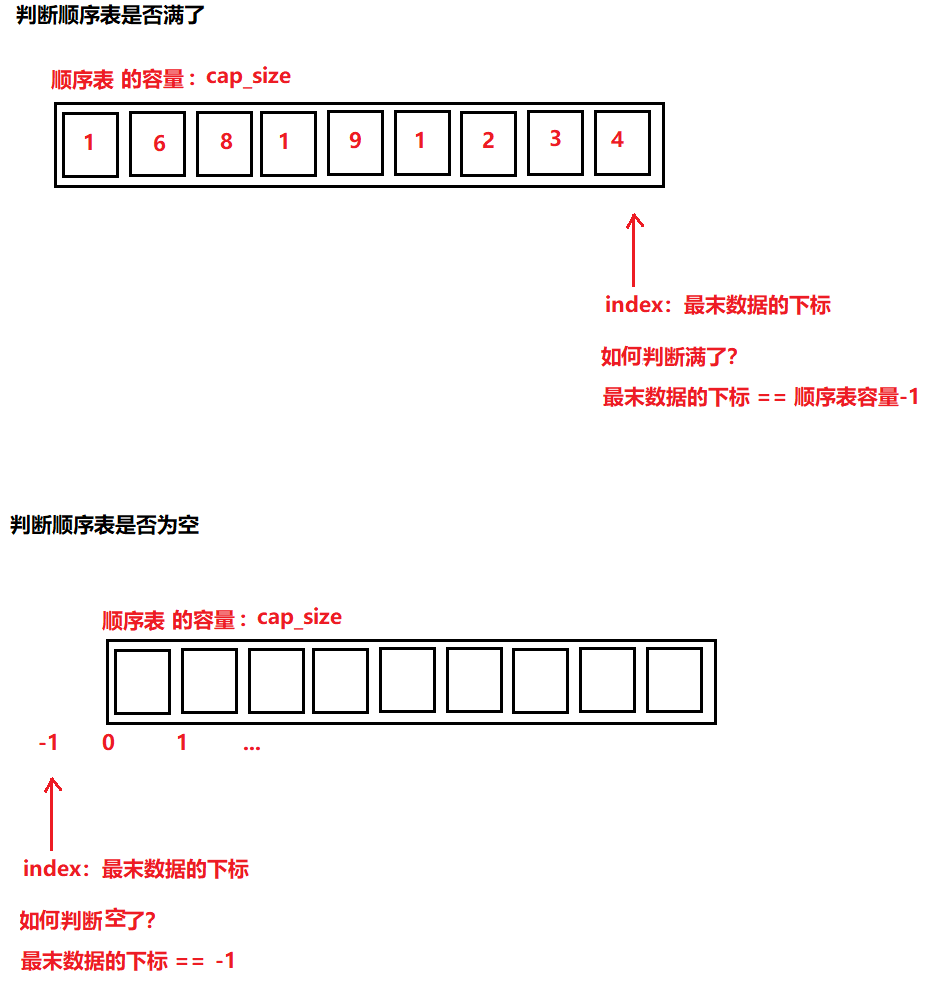
说明:
需要先判断顺序表是否满了,这样可以决定是否还可以增加数据,判断其是否空了,这样可以决定是否还需要删除数据
图解:
代码:
/** * @brief 判断顺序表数据是否满了 * @note None * @param p:顺序表管理结构体的指针 * @retval 顺序表数据满了:返回true * 顺序表数据未满:返回false */ bool SEQUENTIAL_LIST_IfFull(sq_list_p p) { return p->index == p->capacity-1; } /** * @brief 判断顺序表数据是否空了 * @note None * @param p:顺序表管理结构体的指针 * @retval 顺序表数据为空:返回true * 顺序表数据未空:返回false */ bool SEQUENTIAL_LIST_IfEmpty(sq_list_p p) { return p->index == -1; }(5)插入数据
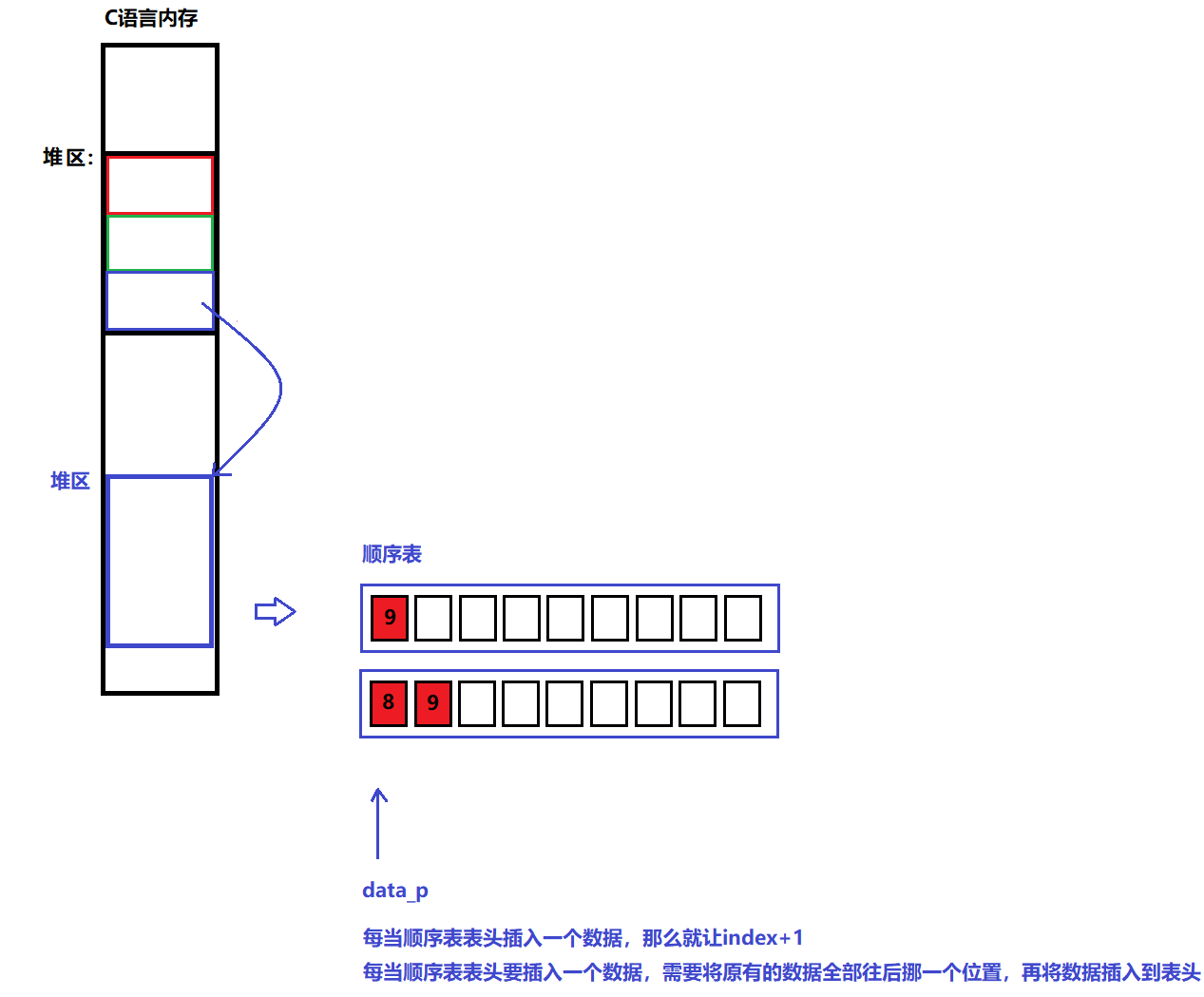
说明:
当我们将数据插入到表头的时候,顺序表后面的数据依次向后退
图解:
代码:
/** * @brief 在顺序表中的表头插入一个数据 * @note None * @param p: 顺序表管理结构体的指针 * new_data:要插入的数据 * @retval 成功:返回0 * 失败:返回-1 */ int SEQUENTIAL_LIST_InsertData(sq_list_p p, int new_data) { // 1、判断顺序表数据是否满了,满了返回-1 if (SEQUENTIAL_LIST_IfFull(p)) return -1; // 2、将原有的数据全部往后挪一个位置,再将数据插入到表头中 for (int i = p->index; i>=0; i--) { p->data_p[i+1] = p->data_p[i]; } // 3、将数据插入到表头 p->data_p[0] = new_data; // 4、顺序表的数据下标index+1 p->index++; // 5、成功返回0 return 0; }(6)删除数据
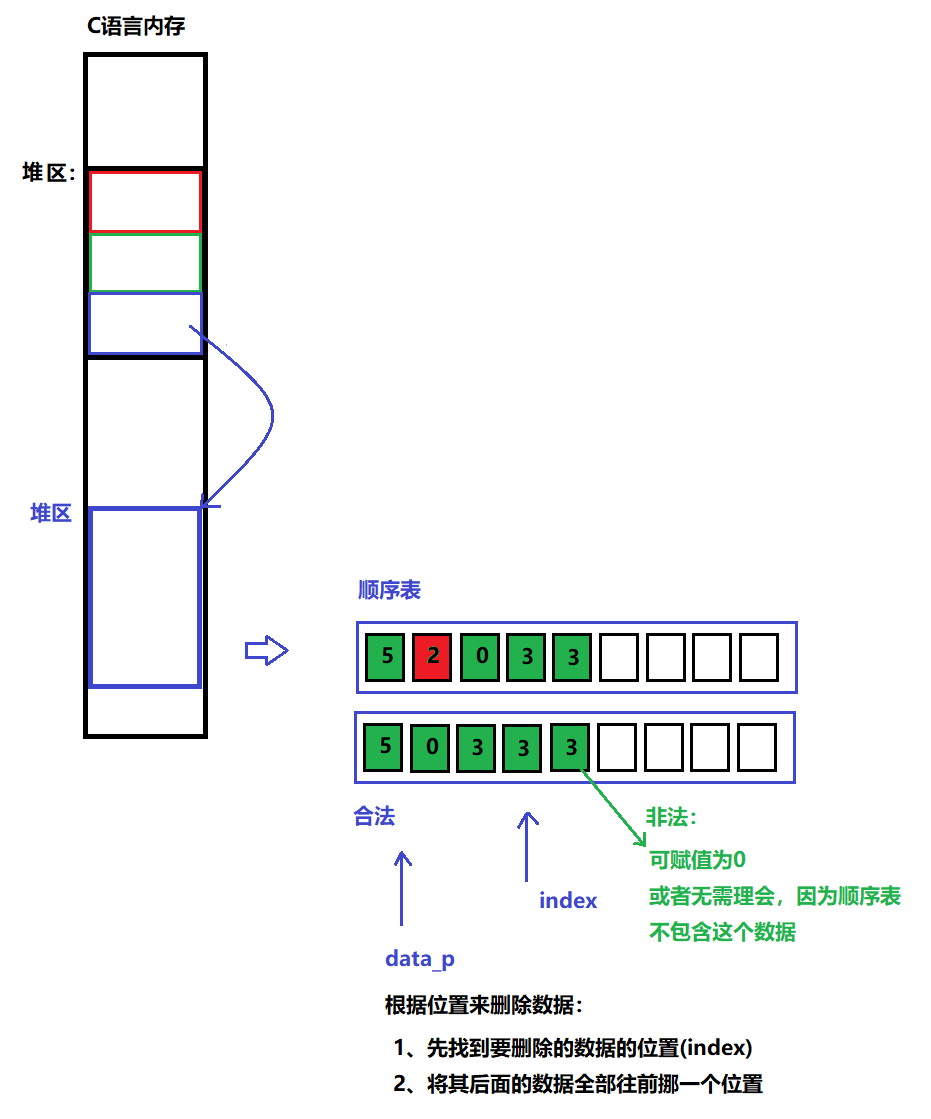
说明:
根据顺序表的位置,将其数据删除(将要删除的数据的后面的数据全部往前挪一个位置)
图解:
示例代码:
/** * @brief 将顺序表指定的位置的数据删除 * @note None * @param p: 顺序表管理结构体的指针 * data_pos:要删除的顺序表数据的位置 * @retval 成功:返回0 * 失败:返回-1 */ int SEQUENTIAL_LIST_DelPosData(sq_list_p p, unsigned int data_pos) { // 1、如果顺序表里面没有数据,并且没有这个位置的数据,就返回-1 if ( (SEQUENTIAL_LIST_IfEmpty(p)) || (data_pos>(p->index)) ) return -1; // 2、根据要删除的数据的位置,将其后面的数据全部往前挪动一个位置即可 for (int i = data_pos; i<=p->index; i++) { p->data_p[i] = p->data_p[i+1]; } // 3、将下标index-1 p->index--; // 4、成功删除数据,返回0 return 0; }(7)遍历数据
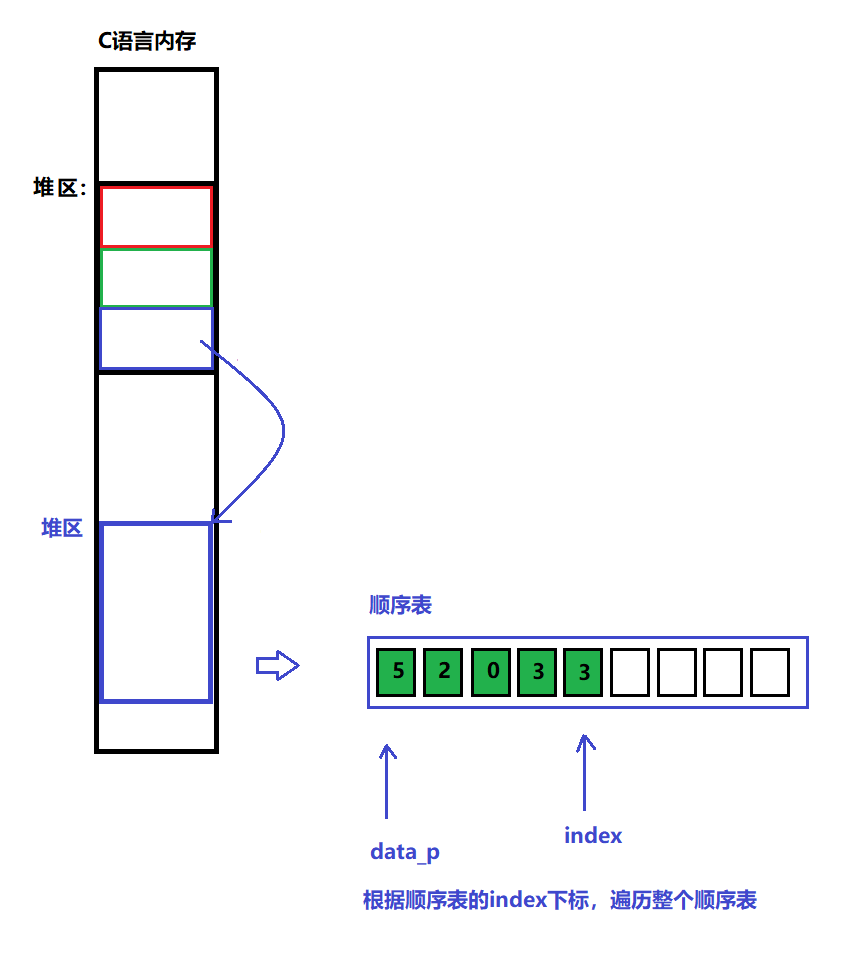
说明:
获取顺序表里面现在的存有的数据
图解:
代码:
/** * @brief 遍历顺序表 * @note None * @param p: 顺序表管理结构体的指针 * @retval None */ void SEQUENTIAL_LIST_ShowList(sq_list_p p) { printf("==================顺序表里面的数据====================\n\n"); for (int i = 0; i<=p->index; i++) { printf("顺序表里面的内存的数据data_p[%d] == %d\n", i, p->data_p[i]); } printf("====================================================\n\n"); }(8)修改数据
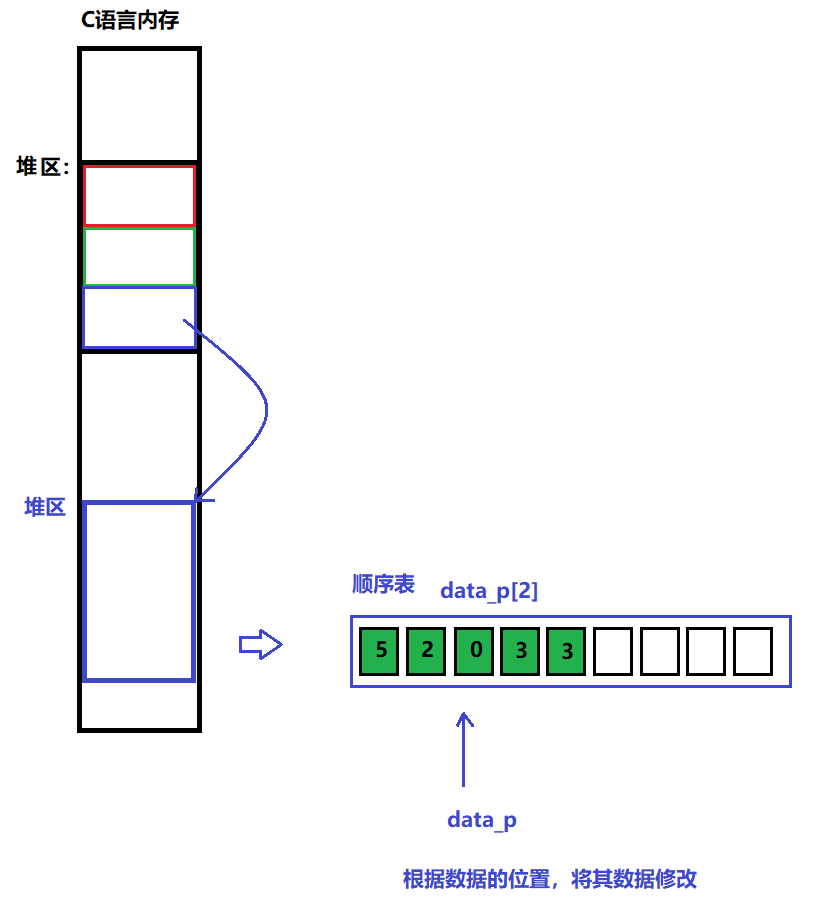
说明:
根据位置来修改顺序表中的数据
图解:
代码:
/** * @brief 修改顺序表中的数据 * @note 根据数据的位置来修改数据 * @param p: 顺序表管理结构体的指针 * data_pos: 要修改的顺序表数据的位置 * change_data:修改后的数据 * @retval 成功:返回0 * 失败:返回-1 */ int SEQUENTIAL_LIST_ChangeData(sq_list_p p, int data_pos, int change_data) { // 1、判断顺序表是否为空 if ( (SEQUENTIAL_LIST_IfEmpty(p)) || (data_pos>(p->index))) return -1; // 2、根据位置,修改数据 p->data_p[data_pos] = change_data; // 3、成功返回0 return 0; }
顺序表请看下回笔记