一、逻辑回归简洁:解决‘二选一’的分类问题
1.核心定位
逻辑回归的核心作用是判断样本属于两个类别中的哪一个(比如 “是 / 否”“好 / 坏”“流失 / 不流失”),无法直接处理多分类问题(多分类需通过 “一对多”“一对一” 等策略扩展)。
2.常见应用场景(结合生活案例)
医疗健康:预测疾病(如新冠阳性 / 阴性、肿瘤良性 / 恶性)。比如通过患者的体温、血常规指标,判断是否感染病毒;
金融风控:银行贷款审批(放贷 / 不放贷)。根据申请人的收入、征信记录、负债情况,评估违约风险,决定是否放款;
情感分析:社交媒体评论判断(正面 / 负面)。比如分析用户对某部电影的评论,判断用户是 “推荐” 还是 “不推荐”;
互联网营销:广告点击率预测(点击 / 不点击)。根据用户的浏览历史、年龄、地域,预测用户是否会点击某则商品广告;
扩展场景:电商平台 “用户是否复购”、运营商 “客户是否流失”、招聘 “候选人是否入职” 等,只要是 “二选一” 的问题,都可以用逻辑回归初步解决。
3.数学基础应用:逻辑回归的“底层逻辑”
逻辑回归的推导依赖 4 个核心数学概念,这些概念不是 “空中楼阁”,可以结合生活场景理解:
(1)sigmoid函数:把任意数标出“概率”
作用:将线性回归输出的 “任意实数”(范围(-∞, +∞),映射到(0,1)之间,最终结果可理解为 “样本属于正类的概率”(比如概率 0.8 表示有 80% 概率是阳性)
数学公式 : ![]() 其中x是线性回归的输出(x = w1x1+w2x2+...+wnxn+b)
其中x是线性回归的输出(x = w1x1+w2x2+...+wnxn+b)
关键性质:单调递增,拐点在(0,0.5)当x = 0,f(x) = 0.5(可理解为 “判断边界”,概率 > 0.5 归为正类,否则归为负类);类比考试分数(通过线性回归输出),通过sigmoid函数转化为 “及格概率”—— 分数越高,及格概率越接近 1,分数越低越接近 0。
(2)概率:事件发生的“可能性”
基础概念:比如抛硬币正面朝上的概率是 0.5,明天下雨的概率是 0.3,逻辑回归的输出就是 “样本属于正类的概率”。
联合概率:多个事件同时发生的概率。比如 “明天既下雨又刮风” 的概率,在逻辑回归中,用于计算 “所有样本都分类正确” 的概率(后续极大似然估计会用到)。
(3)极大似然估计:“根据结果猜原因”
核心思想:已知观测到的结果,反推 “最可能导致这个结果的模型参数”。
生活案例:抛出一枚不均匀的硬币 6 次,结果是 “正、反、反、正、正、正”(3 次正,3 次反),求 “正面朝上的概率θ”。
思路:“什么样的θ能让‘3 正 3 反’这个结果最可能发生?”—— 通过计算可知,当θ时,这个结果的概率最大(虽硬币不均匀,但观测结果恰好平衡,暂估θ)。
在逻辑回归中的作用:通过 “所有样本分类正确的联合概率最大”,反推最优的特征权重w和偏置b(这是逻辑回归训练的核心目标)。
(4)对数函数:把“乘法”变成“加法”
核心作用:简化计算,极大似然估计中,“联合概率” 是多个样本概率的乘积(比如 1000 个样本,就是 1000 个概率相乘),数值会非常小(容易出现 “数值下溢”);通过对数函数,可将 “乘积” 转化为 “加法”(log(ab)=log a + log b),既简化计算,又避免数值问题。
关键性质:
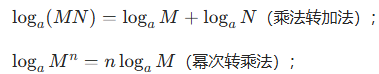
二、逻辑回归原理:从“线性回归”到“分类”
逻辑回归可以理解为 “线性回归 + sigmoid 函数” 的组合,核心是 “用线性模型拟合特征,用 sigmoid 函数输出概率,用极大似然估计求最优参数”。
1.先拟合,再概率化
第一步:用线性回归拟合特征与标签的关系,得到线性输出x = w1x1+w2x2+...+wnxn+b;
第二步:将线性输出x输入 sigmoid 函数,得到 “样本属于正类的概率”p=f(x)= 1/(1+e**(-x))
第三步:根据概率判断类别 —— 若(p>0.5),归为正类(比如 “流失”);若(p<0.5),归为负类(比如 “不流失”)。
2.预测过程案例:判断是否恶性
假设我们有 3 个样本,特征是 “肿瘤大小”“细胞异形率”,标签是 “是否恶性”(1 = 恶性,0 = 良性):
| 样本 | 肿瘤大小(x1) | 细胞异形率(x2) | 线性输出 x=0.2x1+0.3x2+0.1 | sigmoid 概率 p | 预测类别(阈值 0.5) | 真实类别 |
|---|---|---|---|---|---|---|
| 1 | 2.0 | 1.0 | 0.22 + 0.31 + 0.1=0.8 | ≈0.69 | 1(恶性) | 1 |
| 2 | 1.0 | 0.5 | 0.21 + 0.30.5 + 0.1=0.45 | ≈0.61 | 1(恶性) | 0 |
| 3 | 0.5 | 0.3 | 0.20.5 + 0.30.3 + 0.1=0.39 | ≈0.59 | 1(恶性) | 0 |
通过这个案例可以看到:逻辑回归的预测过程,本质是 “先算线性得分,再转概率,最后定类别”。
3.损失函数:衡量“预测值与真实值的差距”
损失函数是 “评估模型预测错误程度” 的指标,逻辑回归用对数似然损失函数(区别于线性回归的均方误差),核心思路是 “让‘所有样本分类正确的概率’最大”。
(1)单个样本的损失
假设样本真实类别为y(1=正类,0=负类),模型预测的正类概率为p:
若y=1(真实是正类):希望p越大越好,损失为-log(p)(p越接近 1,损失越接近 0;p越接近 0,损失越大);
若y=0(真实是负类):希望(1-p)越大越好(即p越小越好),损失为(-log(1-p))(p越接近 0,损失越接近 0;p越接近 1,损失越大);
合并公式:Loss = -[ylog(p) + (1-y)log(1-p)](这个公式能覆盖两种情况,非常简洁)
(2)多个样本的总损失
总损失是所有样本损失的平均值(或总和):
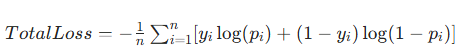
其中n是样本数量,yi是滴i个样本的真实类别,pi是滴i个样本的预测概率。
(3)损失函数的优化:梯度下降
逻辑回归的训练目标是 “最小化总损失”,常用梯度下降算法:
核心思想:沿着损失函数的 “梯度方向”(即损失下降最快的方向),逐步调整特征权重w和偏置b;
过程类比:比如从山顶下山,每次都往 “最陡” 的方向走一小步,直到走到山底(损失最小);
最终结果:通过多次迭代,找到让总损失最小的w和b,此时模型的预测效果最好。
三、逻辑回归API:用Python快速实现
在 Python 中,我们用scikit-learn(简称 sklearn)库的LogisticRegression类实现逻辑回归,掌握参数含义和使用流程是关键。
1.核心API参数解析
sklearn.linear_model.LogisticRegression(solver='liblinear', penalty='l2', C=1.0)
| 参数 | 作用 | 常用取值与说明 |
|---|---|---|
solver |
损失函数的优化方法(即 “如何找到最优参数w和b”) | - liblinear:适合小数据集(样本数 < 1 万),训练快; - sag/saga:适合大数据集,支持并行计算; - newton-cg:适合多分类,只支持 L2 正则化 |
penalty |
正则化类型(防止模型 “过拟合”,即模型在训练集上表现好,测试集上差) | - l2:默认值,对权重做 “平方惩罚”(权重越大,惩罚越重); - l1:对权重做 “绝对值惩罚”,可实现特征选择(让不重要特征的权重为 0) |
C |
正则化力度(与惩罚强度成反比) | - C越大:正则化越弱(模型越容易过拟合); - C越小:正则化越强(模型越保守,可能欠拟合) |
| 其他注意点 | 默认将 “类别数量少的类” 视为正类(比如样本中 “恶性肿瘤” 占 30%,“良性” 占 70%,则正类是 “恶性肿瘤”) |
2.实战案例:癌症分类预测
(1)数据描述
数据集:威斯康星乳腺癌数据集,共 699 条样本,11 列数据;
特征:9 个医学指标(如 “肿块厚度”“细胞大小均匀性” 等);
标签:2 = 良性,4 = 恶性;
缺失值:16 个缺失值,用 “?” 标记。
(2)实现流程(代码+解释)
# 1. 导入需要的库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split # 分割训练集/测试集
from sklearn.preprocessing import StandardScaler # 特征标准化(逻辑回归需要)
from sklearn.linear_model import LogisticRegression # 逻辑回归模型
from sklearn.metrics import accuracy_score # 准确率评估
# 2. 数据加载与预处理
# 2.1 读取数据(假设数据文件在./data目录下)
data = pd.read_csv('./data/breast-cancer-wisconsin.csv')
# 2.2 处理缺失值:将“?”替换为NaN,然后删除含NaN的行
data = data.replace(to_replace="?", value=np.NaN)
data = data.dropna()
# 2.3 划分特征(x)和标签(y):特征是第1-9列,标签是最后一列
x = data.iloc[:, 1:-1] # 第1列是ID(无用),所以从第2列开始取
y = data["Class"] # 标签列
# 2.4 分割训练集(70%)和测试集(30%):random_state固定随机种子,保证结果可复现
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=22)
# 3. 特征工程:标准化(逻辑回归对特征尺度敏感,需将特征缩放到均值0、方差1)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train) # 训练集:先拟合(算均值方差)再转换
x_test = transfer.transform(x_test) # 测试集:用训练集的均值方差转换(避免数据泄露)
# 4. 模型训练与预测
# 4.1 实例化模型:用默认参数(solver='liblinear',penalty='l2')
estimator = LogisticRegression()
# 4.2 训练模型:用训练集学习参数
estimator.fit(x_train, y_train)
# 4.3 预测测试集:得到预测类别
y_pred = estimator.predict(x_test)
# 5. 模型评估:计算准确率(正确预测的样本数/总样本数)
accuracy = accuracy_score(y_test, y_pred)
print(f"测试集准确率:{accuracy:.2f}") # 通常准确率会在95%以上,效果较好(3)关键注意点
特征标准化:逻辑回归的目标函数是 “对数似然损失”,特征尺度差异会导致权重更新不均衡(比如 “收入” 是 1 万量级,“年龄” 是 10 量级,权重会偏向 “收入”),所以必须做标准化;
缺失值处理:本例用 “删除法”,但实际中也可根据业务用 “均值填充”“中位数填充”(比如医学数据常用中位数,避免极端值影响)
随机种子:random_state=22保证每次运行代码,训练集 / 测试集的分割结果一致,方便调试。
四、分类问题评估:不止“准确率”
在分类问题中,“准确率”(正确预测数 / 总样本数)往往不够用 —— 比如癌症检测中,“漏诊”(将恶性预测为良性)的代价远大于 “误诊”(将良性预测为恶性),此时需要更精细的评估指标。
1.混淆矩阵:分类结果的“全景图”
混淆矩阵是 4 个核心指标的组合,能清晰展示模型的分类错误类型,以 “正类 = 恶性肿瘤,负类 = 良性肿瘤” 为例:
| 真实值 \ 预测值 | 正类(恶性) | 负类(良性) |
|---|---|---|
| 正类(恶性) | TP(真正例) | FN(假反例) |
| 负类(良性) | FP(假正例) | TN(真反例) |
TP(True Positive):真实是正类,预测为正类(正确检测出恶性,好结果);
FN(False Negative):真实是正类,预测为负类(漏诊,恶性预测为良性,坏结果);
FP(False Positive):真实是负类,预测为正类(误诊,良性预测为恶性,相对坏结果);
TN(True Negative)真实是负类,预测为负类(正确检测出良性,好结果)。
假设有10个样本,用下例两个模型来对比
模型A:预测对 3 个恶性,4 个良性
混淆矩阵:TP=3,FN=3(漏诊 3 个恶性),FP=0(无误诊),TN=4
→ 问题:漏诊率高,可能延误治疗;
模型B:预测对 6 个恶性,1 个良性
混淆矩阵:TP=6,FN=0(无漏诊),FP=3(误诊 3 个良性),TN=1
→ 问题:误诊率高,会让患者不必要恐慌,但漏诊率低(更适合癌症检测)。
通过混淆矩阵可见:只看准确率(模型 A 准确率 70%,模型 B 准确率 70%),无法区分模型优劣,必须结合业务场景选择 “漏诊率低” 或“误诊率低”的模型。
2.精确率、召回率、F1-score:聚焦核心需求
基于混淆矩阵,衍生出 3 个关键指标,分别对应不同业务场景的需求:
(1)精确率(Precision):“预测为正类的样本中,真正是正类的比例”
公式:![]() (分子是 “真阳性”,分母是 “所有预测为阳性的样本”)
(分子是 “真阳性”,分母是 “所有预测为阳性的样本”)
含义:衡量 “预测正类的准确性”,避免 “误判”。
比如垃圾邮件过滤场景:希望 “预测为垃圾邮件的样本中,真正是垃圾邮件的比例高”(否则会把正常邮件误判为垃圾邮件,用户体验差)。
上述两个案例计算:
模型A:P=3/3+0 = 100%(无误诊,精确率高);
模型B:P=6/3+6 = 67%\(Precision = \frac{6}{6+3} = 67\%\)(有 3 个误诊,精确率低)。
模型 B 的 F1-score 更高,综合性能更好(更适合癌症检测)。
(2)召回率(Recall,又称查全率):“真实为正类的样本中,被预测为正类的比例”
公式: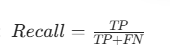 (分子是 “真阳性”,分母是 “所有真实阳性的样本”)
(分子是 “真阳性”,分母是 “所有真实阳性的样本”)
含义:衡量 “正类样本的覆盖能力”,避免 “漏判”。比如癌症检测、欺诈检测场景:希望 “所有真实恶性肿瘤 / 欺诈交易,都能被检测出来”(漏判的代价远大于误判)。
案例计算:
模型A:R=3/3+3 = 50%(漏诊 3 个,召回率低);
模型B:R=6/6+0=100%(无漏诊,召回率高);
(3)F1-score:精确率与召回率的“调和平均数”
问题:精确率和召回率往往 “此消彼长”—— 比如模型 B 为了提高召回率(不漏诊),会把更多样本预测为正类,导致精确率下降;模型 A 为了提高精确率(不误诊),会把更多样本预测为负类,导致召回率下降。
解决方案:F1-score 综合两者,当精确率和召回率都高时,F1-score 才高,避免 “偏科”。
公式:![]()
案例计算:
模型A:F1=2*100%*50%/100%+50%=67%
模型B:F1 = 2*67%*67%/67%+67%=80%
模型 B 的 F1-score 更高,综合性能更好(更适合癌症检测)。
(4)API实现(sklearn)
from sklearn.metrics import precision_score, recall_score, f1_score
# 假设y_test是真实标签,y_pred是模型预测标签,pos_label指定“正类”(比如“恶性”)
precision = precision_score(y_test, y_pred, pos_label="恶性")
recall = recall_score(y_test, y_pred, pos_label="恶性")
f1 = f1_score(y_test, y_pred, pos_label="恶性")
print(f"精确率:{precision:.2f}")
print(f"召回率:{recall:.2f}")
print(f"F1-score:{f1:.2f}")
3.ROC曲线与AUC指标:评估“概率排序能力”
前面的指标依赖 “分类阈值”(比如概率 > 0.5 为正类),但实际中阈值可能需要调整(比如癌症检测可将阈值调低到 0.3,进一步降低漏诊率)。ROC 曲线和 AUC 指标则可以 “不依赖阈值”,评估模型的整体分类能力。
(1)核心概念:TPR与FPR
TPR(真正率,Recall的别名):![]() (真实正类中被正确预测的比例,越高越好);
(真实正类中被正确预测的比例,越高越好);
FPR(假正率):![]() (真实负类中被错误预测为正类的比例,越低越好)。
(真实负类中被错误预测为正类的比例,越低越好)。
(2)ROC曲线:不同阈值的“TPR-FPR”曲线
绘制逻辑:从 “阈值 = 1”(所有样本预测为负类,TPR=0,FPR=0)到 “阈值 = 0”(所有样本预测为正类,TPR=1,FPR=1),调整阈值,计算每个阈值对应的 TPR 和 FPR,连成曲线。
曲线解读:曲线越靠近左上角(TPR 高,FPR 低),模型性能越好;对角线(TPR=FPR):模型性能等同于 “随机猜测”(比如抛硬币判断类别);曲线在对角线下方:模型性能比随机猜测差(通常是正类 / 负类标签搞反了)。
(3)AUC指标:ROC曲线下的“面积”
含义:AUC 是 ROC 曲线与横轴围成的面积,范围在 [0,1] 之间,直接量化模型的整体性能:
AUC=1:完美分类器(所有正类都排在负类前面,无任何错误);
AUC=0.5:随机分类器(和抛硬币一样);
AUC>0.8:优秀分类器;
AUC<0.5:性能差,可通过反转标签改善。
生活类比:比如广告点击率预测,AUC 越高,说明 “模型能把‘会点击的用户’排在‘不会点击的用户’前面” 的能力越强,广告投放效率越高。
(4)案例:广告点击预测的ROC曲线绘制
假设广告展示 6 次,正样本(点击)2 个(样本 1、3),负样本(未点击)4 个(样本 2、4、5、6),模型预测的点击概率如下:
| 样本 | 真实标签(点击 = 1) | 预测点击概率 |
|---|---|---|
| 1 | 1 | 0.9 |
| 2 | 0 | 0.7 |
| 3 | 1 | 0.8 |
| 4 | 0 | 0.6 |
| 5 | 0 | 0.5 |
| 6 | 0 | 0.4 |
步骤1:按预测概率降序排序:样本 1(0.9)→样本 3(0.8)→样本 2(0.7)→样本 4(0.6)→样本 5(0.5)→样本 6(0.4);
步骤2:调整阈值,计算 TPR 和 FPR:
阈值=0.95:无样本预测为正类 → TPR=0/2=0,FPR=0/4=0 → 点 (0,0);
阈值=0.85:仅样本 1 预测为正类 → TPR=1/2=0.5,FPR=0/4=0 → 点 (0,0.5);
阈值= 0.75:样本 1、3 预测为正类 → TPR=2/2=1,FPR=0/4=0 → 点 (0,1);
阈值=0.65:样本 1、3、2 预测为正类 → TPR=2/2=1,FPR=1/4=0.25 → 点 (0.25,1);
阈值=0.55:样本 1、3、2、4 预测为正类 → TPR=2/2=1,FPR=2/4=0.5 → 点 (0.5,1);
阈值= 0.45:样本 1、3、2、4、5 预测为正类 → TPR=2/2=1,FPR=3/4=0.75 → 点 (0.75,1);
阈值= 0.35:所有样本预测为正类 → TPR=2/2=1,FPR=4/4=1 → 点 (1,1);
步骤3:连接所有点,得到 ROC 曲线:曲线几乎紧贴左上角,AUC 接近 1,说明模型对 “点击用户” 的识别能力很强。
(5)API实现(sklearn)
from sklearn.metrics import roc_auc_score, roc_curve
import matplotlib.pyplot as plt
# 1. 计算AUC值(需要模型输出的概率,而非类别)
# estimator.predict_proba(x_test)[:,1]:输出所有样本属于正类的概率
y_score = estimator.predict_proba(x_test)[:, 1]
auc = roc_auc_score(y_test, y_score)
print(f"AUC值:{auc:.2f}")
# 2. 绘制ROC曲线
fpr, tpr, thresholds = roc_curve(y_test, y_score, pos_label="恶性") # 计算FPR、TPR、阈值
plt.plot(fpr, tpr, label=f"AUC = {auc:.2f}") # 绘制ROC曲线
plt.plot([0,1], [0,1], 'r--') # 绘制随机猜测的对角线
plt.xlabel("假正率(FPR)")
plt.ylabel("真正率(TPR)")
plt.title("ROC曲线")
plt.legend()
plt.show()