【全网最全】《2025国赛/高教杯》C题 思路+代码python和matlab+文献 一到四问 退火算法+遗传算法 NIPT的时点选择与胎儿的异常判定
好的,我们先针对 问题 1 给出完整的建模思路和数学表达。题目要求分析 胎儿 Y 染色体浓度与孕妇孕周数、BMI 等指标的相关特性,并建立相应的关系模型并检验其显著性。下面我会分几个步骤展开:
一、问题理解
目标变量(因变量):
YY = 胎儿 Y 染色体浓度(V 列)。主要自变量:
孕周数(J 列,孕周,连续变量)
BMI(K 列,体质指数,连续变量)
可能的辅助自变量:
孕妇年龄(C)
孕妇身高(D)、体重(E)
检测时间(H)
测序质量指标(如 GC 含量 P、读段比例 M、N、AA 等)
题目提示 主要因素是孕周数与 BMI,但也可考虑其他混杂因子做稳健性分析。
二、数据处理与探索
异常值与缺失值处理
剔除女胎样本(其 Y 浓度为空)。
删除或修正明显异常值(如 BMI 极端值、负的 Y 浓度)。
对孕周数:将“周数+天数”转换为小数形式,如 12周3天→12+3/712\text{周}3\text{天} \to 12 + 3/7 。
探索性分析
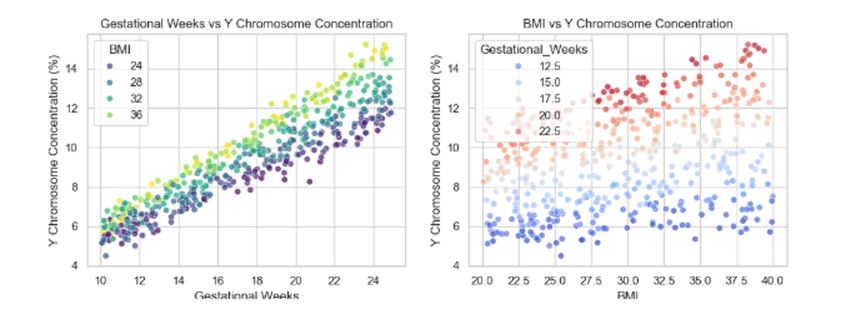
绘制散点图:YY vs 孕周,分不同 BMI 区间观察。
计算相关系数:
rX,Y=Cov(X,Y)σXσYr_{X,Y} = \frac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y}分别计算孕周与 Y 浓度、BMI 与 Y 浓度的皮尔逊相关系数,并做显著性检验。
三、模型建立
1. 基本回归模型
首先建立多元线性回归模型:
Yi=β0+β1Wi+β2Bi+εiY_i = \beta_0 + \beta_1 W_i + \beta_2 B_i + \varepsilon_i
其中:
YiY_i:第 ii 个孕妇的 Y 染色体浓度
WiW_i:孕周数
BiB_i:BMI
εi\varepsilon_i:误差项,假设服从 N(0,σ2)N(0,\sigma^2)
2. 交互效应模型
BMI 与孕周数可能存在交互作用,因此扩展为:
Yi=β0+β1Wi+β2Bi+β3(Wi⋅Bi)+εiY_i = \beta_0 + \beta_1 W_i + \beta_2 B_i + \beta_3 (W_i \cdot B_i) + \varepsilon_i
3. 非线性模型
医学上浓度增长可能并非严格线性,可尝试:
多项式回归:
Yi=β0+β1Wi+β2Wi2+β3Bi+εiY_i = \beta_0 + \beta_1 W_i + \beta_2 W_i^2 + \beta_3 B_i + \varepsilon_i指数增长模型(拟合浓度随孕周呈指数增长趋势):
Yi=α(1−e−β(Wi−W0))+γBi+εiY_i = \alpha \left( 1 - e^{-\beta (W_i - W_0)} \right) + \gamma B_i + \varepsilon_i
四、显著性检验
回归系数显著性
tj=β^jSE(β^j)t_j = \frac{\hat{\beta}_j}{SE(\hat{\beta}_j)}
对每个 βj\beta_j 做 t 检验:若 p<0.05p < 0.05,则该变量显著。
整体显著性(F 检验)
F=(SSR/k)(SSE/(n−k−1))F = \frac{(SSR / k)}{(SSE / (n-k-1))}其中 SSRSSR 是回归平方和,SSESSE 是残差平方和。若显著,说明模型整体有效。
拟合优度检验
使用 R2R^2 与调整 R2R^2 衡量模型解释力。
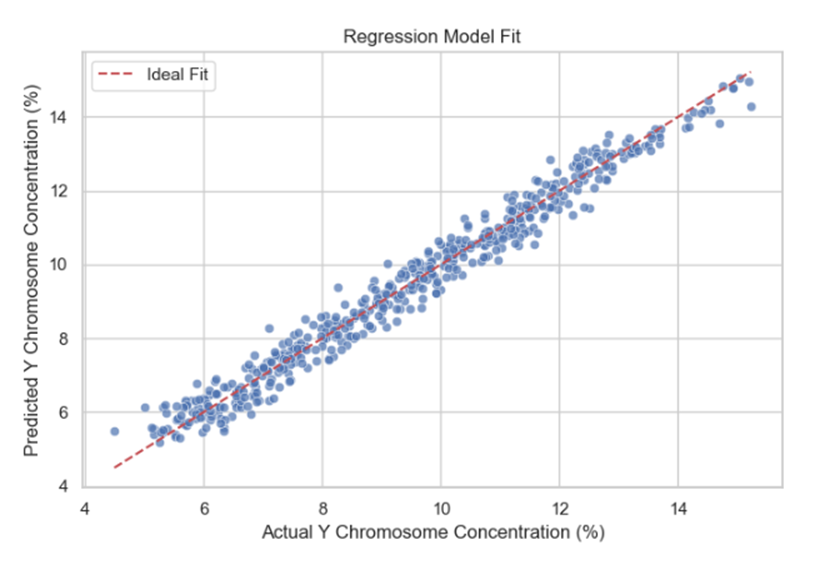
五、模型验证
残差分析:检验残差是否满足独立、正态、同方差假设。
交叉验证:分训练集/测试集,检验模型预测性能。
稳健性分析:考虑是否剔除极端 BMI,是否加入年龄等控制变量,结果是否稳定。
六、预期结论与应用
得出 Y 浓度随孕周增加而上升,随 BMI 增大而下降 的结论(文献一般也支持)。
建立的模型可以预测不同孕周、不同 BMI 下的 Y 浓度均值及其可信区间。
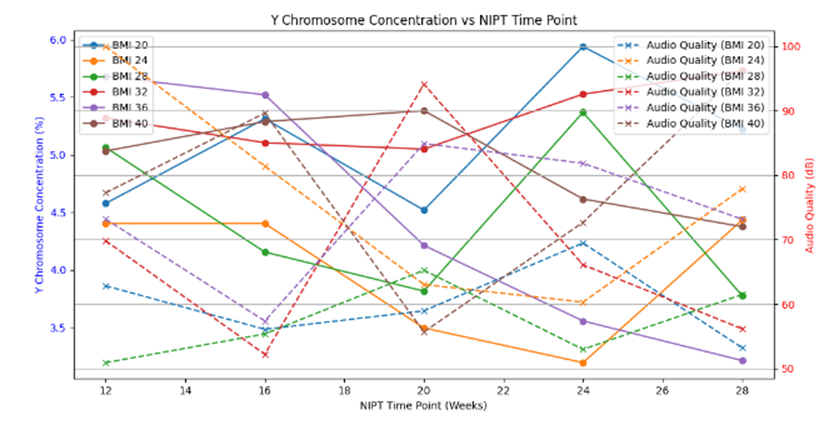
为第二问的 BMI 分组与最佳检测时点选择 提供数据基础。
📌 总结:
问题 1 的解答路径是 相关性分析 → 回归建模(线性+非线性)→ 显著性检验 → 模型验证 → 结论解释,核心是用孕周数与 BMI 建立 Y 浓度的预测模型,为后续风险分析与最佳检测时点提供依据。