一、多项式的描述与运算
1.1 多项式的描述
(1)直接输入法
在MATLAB环境下多项式的表达式为
可以转换为向量的形式加以描述,即


例:请在MATLAB中描述多项式。
在MATLAB中,此多项式可被描述成如下形式:
p=[6 5 0 8]
缺少的各项系数在向量中用0代替。
(2)特征多项式输入法
特征多项式输入法是MATLAB中通过矩阵生成对应特征多项式的常用方法,其核心原理是利用矩阵的特征值构造多项式。
基本原理:
定义依据:对于n阶方阵A,其特征多项式由行列式运算定义,即:
其中为特征值变量,
为单位矩阵。
系数生成规则:生成的系数向量为n+1维行向量,对应降幂排列的多项式系数;首项系数必须为1(即的系数),后续系数由矩阵特征值的性质决定。
特性说明:
矩阵要求:必须为方阵,否则无法计算特征多项式;奇异矩阵的特征多项式可能包含零根。
数值稳定性:对于高阶矩阵(如n>10),由于数值计算误差,可能出现微小虚部,可通过real()函数过滤。
特征值与特征向量的定义
假设矩阵A是n阶方阵,如果存在数和给零向量
,使得
则是矩阵A的一个特征值,X是对应
的一个特征向量。
特征向量的核心特点是:
在矩阵A的线性变换下,方向保持不变(或反向),仅被 “伸缩” 了倍。
(注意:特征向量必须是非零向量,因为零向量代入AX = X时,对任意
都成立,无意义。)
特征矩阵
为特征矩阵。
- E 是n 阶单位矩阵(对角线上全为 1,其余为 0 的方阵);
是对角矩阵(对角线上全为\(\lambda\),其余为 0)。
特征多项式
对特征矩阵取行列式,即计算 ,得到的结果是一个关于
的 n 次多项式,称为矩阵A的特征多项式。
核心联系:
要使 有非零解X,等价于齐次线性方程组
有非零解。根据线性代数知识,“齐次方程组有非零解” 的充要条件是系数矩阵的行列式为 0,即:
这就是特征方程,而特征值正是这个方程的 “根”(解)。


补充:
(1)poly():
1. MATLAB 中的 poly() 函数
MATLAB 中的 poly() 有两个主要用途:
用途 1:根据 “根” 生成多项式
如果输入是一个向量(表示多项式的根),poly() 会返回该多项式的系数(按降幂排列)。
语法:
p = poly(r)
- 输入
r:向量,包含多项式的根(如r = [r1, r2, ..., rn]表示多项式的根为r1, r2, ..., rn)。
- 输出
p:向量,多项式的系数,满足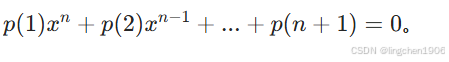 。
。
示例:
若多项式的根为 1 和 3(即 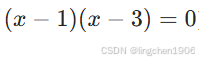 ),则:
),则:
r = [1, 3]; % 根为1和3
p = poly(r); % 生成多项式系数结果 p = [1, -4, 3],对应多项式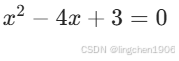 (与前面特征多项式的例子一致)。
(与前面特征多项式的例子一致)。
用途 2:计算矩阵的 “特征多项式”
如果输入是一个方阵,poly() 会返回该矩阵的特征多项式的系数(按降幂排列)。
语法: p = poly(A)
- 输入
A:n 阶方阵。 - 输出
p:向量,特征多项式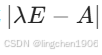 的系数,长度为
的系数,长度为 n+1。
示例:
对前面的矩阵 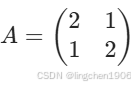 :
:
A = [2 1; 1 2]; % 2阶方阵
p = poly(A); % 计算特征多项式系数结果 p = [1, -4, 3],对应特征多项式 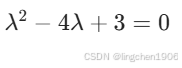 (与手动计算结果一致)。
(与手动计算结果一致)。
2. Python(NumPy)中的 poly() 函数
在 Python 的 numpy 库中,numpy.poly() 功能与 MATLAB 类似,主要用于根据 “根” 生成多项式系数。
语法:
p = numpy.poly(r)
- 输入
r:数组,多项式的根。 - 输出
p:数组,多项式系数(按降幂排列)。
示例:
import numpy as np
r = [1, 3] # 根为1和3
p = np.poly(r)
print(p) # 输出 [ 1 -4 3 ],对应 x² - 4x + 3总结
poly() 函数的核心功能是处理多项式与根的关系:
- 输入 “根” 时,输出多项式的系数(按降幂排列);
- 在 MATLAB 中,输入 “方阵” 时,输出该矩阵的特征多项式系数(这是与线性代数结合的重要应用)。
结合之前的特征值 / 特征多项式知识,poly(A) 是计算矩阵特征多项式的便捷工具,避免了手动展开行列式的繁琐计算。
(2)poly2sym()
在 MATLAB 中,poly2sym 是一个用于将多项式系数向量转换为符号多项式表达式的函数。它的核心作用是 “可视化” 多项式的数学形式,方便进行符号运算或直观展示多项式。
基本语法
sym_poly = poly2sym(p) % 基本用法:将系数向量p转换为关于x的符号多项式
sym_poly = poly2sym(p, var) % 进阶用法:指定变量名(如var='t',生成关于t的多项式)- 输入
p:多项式的系数向量,按降幂排列(即p(1)是最高次项系数,p(end)是常数项)。 - 输出
sym_poly:符号表达式(需要syms符号工具箱支持)。
示例说明
例 1:基本用法(默认变量 x)
假设有一个多项式 ,其系数向量为
,其系数向量为 p = [1, -4, 3](按降幂排列:1 是的系数,-4 是x的系数,3 是常数项)。
syms x % 定义符号变量x(需提前声明)
p = [1, -4, 3]; % 多项式x² -4x +3的系数向量
sym_poly = poly2sym(p); % 转换为符号表达式
disp(sym_poly); % 输出:x^2 - 4*x + 3例 2:指定变量名(如 t)
如果需要生成以 t 为变量的多项式,可以指定第二个参数:
syms t % 定义符号变量t
p = [2, 0, -3, 5]; % 系数向量对应2t³ + 0t² -3t +5
sym_poly = poly2sym(p, t); % 转换为关于t的多项式
disp(sym_poly); % 输出:2*t^3 - 3*t + 5例 3:与poly函数配合使用
结合之前提到的 poly 函数(生成多项式系数),可以快速将矩阵的特征多项式转换为符号形式:
syms lambda % 定义符号变量lambda(常用于特征多项式)
A = [2 1; 1 2]; % 2阶矩阵
p = poly(A); % 用poly计算A的特征多项式系数,结果为[1, -4, 3]
char_poly = poly2sym(p, lambda); % 转换为关于lambda的符号表达式
disp(char_poly); % 输出:lambda^2 - 4*lambda + 3核心作用
poly2sym 的价值在于将 “抽象的系数向量” 转换为 “直观的数学表达式”,尤其适合:
- 展示多项式的结构(如教学、报告中);
- 结合符号工具箱进行多项式的求导、积分、因式分解等符号运算(例如
factor(char_poly)可直接分解特征多项式)。
使用前需确保已通过 syms 定义对应的符号变量,否则可能无法正确生成表达式。
例:已知矩阵M=[2 1 6 ;1 8 9 ;2 4 7 ],求其特征多项式的表达式。

其中,x对应为。
3.由根向量创建多项式
例:已知矩阵a=[4 -3-5i -3+5i],求其对应的多项式表达式。

1.2 多项式的运算
多项式的运算命令如下表:
| 命令 | 功能 |
| polyval(p,x) | 求多项式在x点的取值 |
| polyvalm(p,A) | A矩阵在多项式中的取值 |
| roots(p) | 求多项式的根 |
| polyder | 微分 |
| p1+p2,p1-p2 | 加、减法(项数必须一致) |
| conv | 乘法 |
| deconv | 除法 |
| polyint | 积分 |
例:求多项式在[1 8 9]和[3 5; 7 2]处的值。
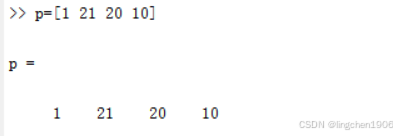
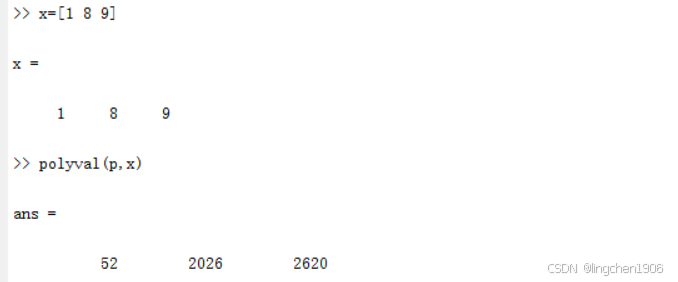

比较运行结果可以发现,polyval是对应元素之间的运算,polyvalm则是按照矩阵的运算规则进行计算。