目录
深度优先搜索我们在二叉树的遍历中学过前序遍历,DFS的一半代码形式就是使用递归,通过复用递归函数的代码来解决重复子问题。 DFS和BFS都是搜索算法,只不过搜索的顺序不太一样,但是他们都是一种暴力搜索的思想,也就是最终都会将解空间的所有节点都一一访问到。
在使用DFS解决问题的时候,递归的思想是重中之重,递归的本质就是函数自己调用自己的情况,而要理解递归,最简单的我们需要从函数展开图来分析,在复杂一点无法绘制展开图的时候,我们可以绘制决策树来解决问题,决策树节点我们只保存关键参数就行了。当这两步我们都能轻易完成时,我们就可以从更宏观的角度来看递归,将其看成一个黑盒,我们将参数丢进去,同时一定能够得到正确的结果,在设计递归的而不去纠结递归函数的具体实现。 而在使用递归来解决问题的时候,最关键的就是发现重复子问题,而递归函数的函数体就是子问题的解决方式,在此基础上,避免写出死递归就行了。
一 基础递归
1 汉诺塔问题

题目解析:本题是递归算法最经典的例题,汉诺塔问题,在柱A上面有n个圆盘,从下到上按照圆盘的从大到小顺序放置,我们需要借助柱 B ,将柱A的圆盘全部转移到柱C上,柱ABC上圆盘都只能按照从下到上,从大到小的顺序放置。
那么我们来分析这个问题,首先我们关注的肯定是 n 的范围,我们可以简单枚举一下n的取值不同,我们的做法有什么区别。
1、 n == 1, 此时意味着柱A只有1个盘子,那么直接将这个盘子从A转移到C就行了。
2、 n == 2, 此时柱A有2个盘子,此时我们要将2个盘子从A转移到C,同时要保证从大到小的顺序,那么我们首先要想办法将 A 的较大的盘子转移到C,那么如何做呢? 此时我们需要将较小的盘子转移到B,那么此时A就可以取出最大的盘子,同时C柱没有盘子,此时就可以将较大的盘子直接从A转移到C,最后我们再将B柱的盘子转移到C。
3、 n == 3, 此时柱A有3个盘子,那么按照上面的思路,我们需要先将A的前两个较小的盘子转移到B柱,然后再将A柱的最大的盘子放到C柱的最下面,最终再将B柱的两个盘子借助A柱来转移到C柱上,那么接下来其实问题就转换为了B柱有2个盘子,A柱为空,而C柱虽然有一个盘子,但是他是最大的一个盘子,我们将任意盘子放在最大的盘子上面都是合法的,所以可以将这个最大的盘子忽略掉,也就是将C也看成空柱,那么问题就变成了将B柱的2个盘子借助A柱转移到C柱上,此时做法同n == 2
4、 n == 4,此时A有4个盘子,我们首先借助C柱将上面的三个盘子转移到B柱,此时问题类比n==3,然后再将最大的盘子放到C柱,接下来就将B柱的三个盘子借助A柱转移到C柱,此时问题类比n==3.
以此类推,我们发现,对于任意的n,我们的做法首先都是将A的n-1个盘子借助C转移到B柱,然后将最大的盘子放到C柱上,由于C柱只有一个最大的盘子同时他已经在最终位置,所以此时C柱虽然有一个盘子,但是我们仍然可以将其看成空柱。此时A柱为空,C柱为空,B柱有n-1个盘子,那么接下来就是将B柱看成初始的A柱,而A柱看成初始情况的B柱,问题就变成了将A的n-1个盘子借助B转移到C,这就是一个重复子问题。
代码如下:
class Solution {
public:
void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
int n = A.size();
dfs(A,B,C,n);
}
void dfs(vector<int>& A, vector<int>& B, vector<int>& C , int n){ //将A的n个盘子借助B转移到C
if(n == 1){ //只有一个盘子的时候直接转移
C.push_back(A.back());
A.pop_back();
return;
}
//当大于1个盘子时
//先将A的n-1个盘子借助C转移到B
dfs(A,C,B,n-1);
//然后将A剩下的最大的盘子直接转移到C
dfs(A,B,C,1); //当然这里也可以直接转移,省去函数栈帧创建与销毁的开销
//最后将B的n-1个盘子借助A转移到C
dfs(B,A,C,n-1);
}
};
2 合并两个有序链表
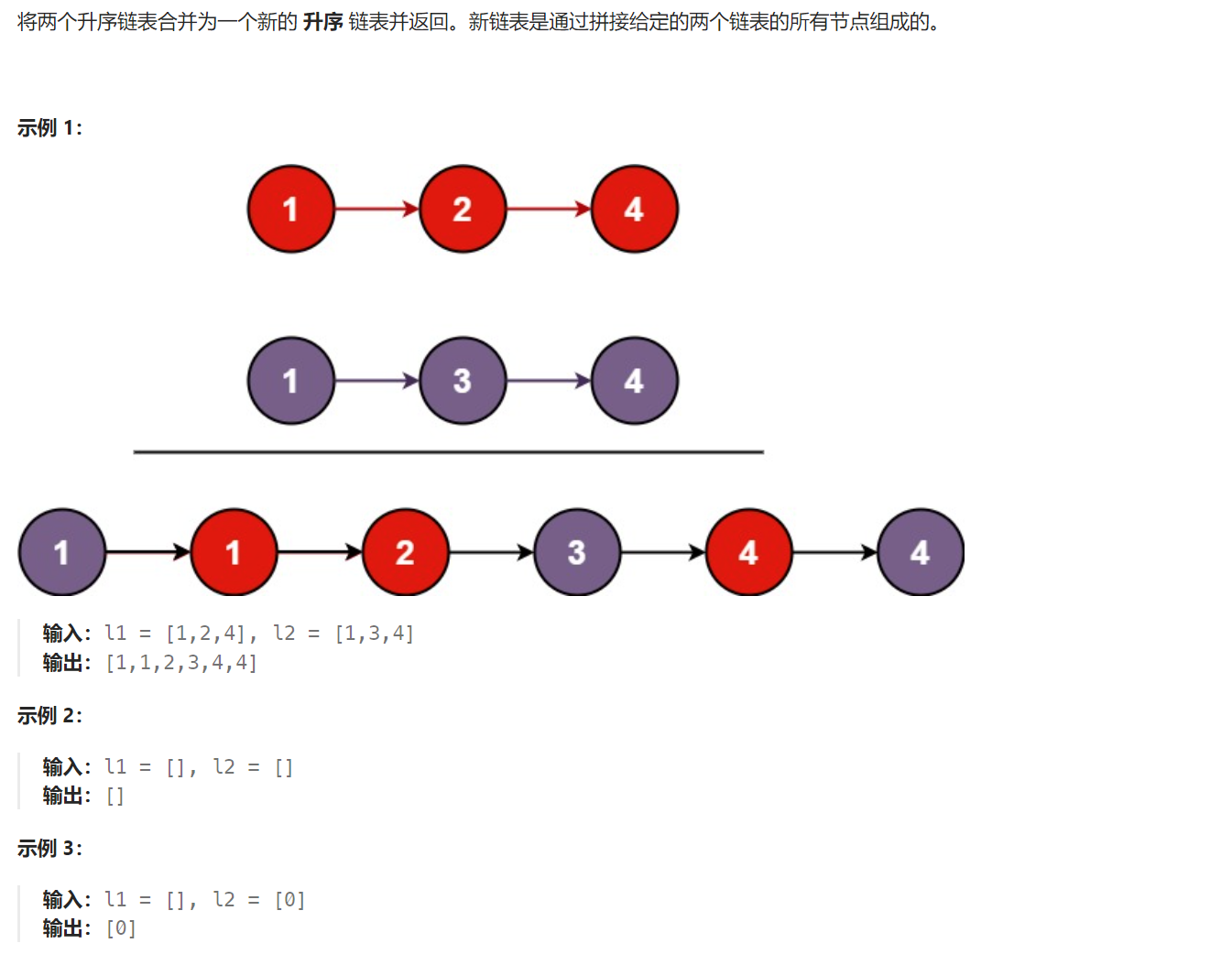
题目解析:给定两个有序链表,要求我们合并成一个后续链表返回。
本题我们使用过归并的思想解决过,但是这里也可以使用递归来做。
其实在合并的过程中,我们每一次都是在选择两个链表的头节点中较小的进行尾插,然后将该头节点从原链表中删除,放到结果链表中。 那么这里的重复子问题就是找两个链表的较小头节点进行尾插,然后更新该链表头节点。而递归的结束条件就是其中一个链表为空,我们直接返回非空的链表。
代码如下:
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
return dfs(l1,l2);
}
ListNode* dfs(ListNode* l1, ListNode* l2){
if(!l1) return l2;
if(!l2) return l1;
//找较小的头节点
ListNode* res = nullptr; //返回的有序链表的头节点
if(l1->val < l2->val){
res = l1;
l1 = l1->next;
}
else{
res = l2 ;
l2 = l2->next;
}
//接下来我们就需要dfs来帮助我们将剩余的l1和l2合并成有序链表,那么尾插在res后面就形成了完整的有序链表
res->next = dfs(l1,l2);
return res;
}
};
3 反转链表
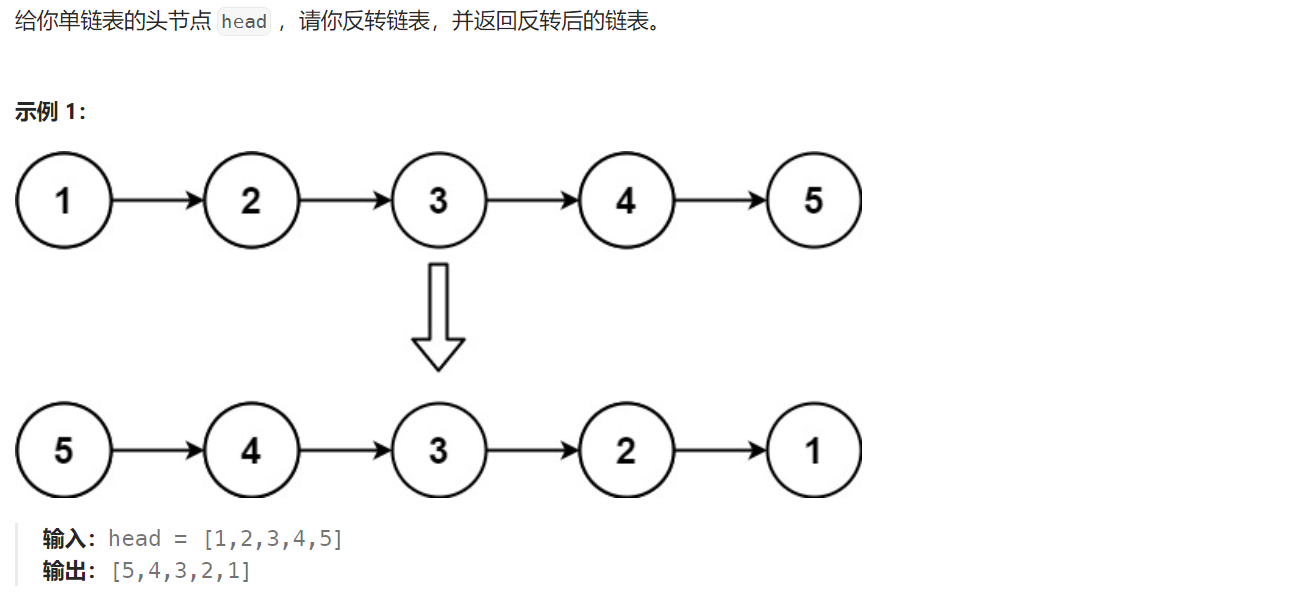
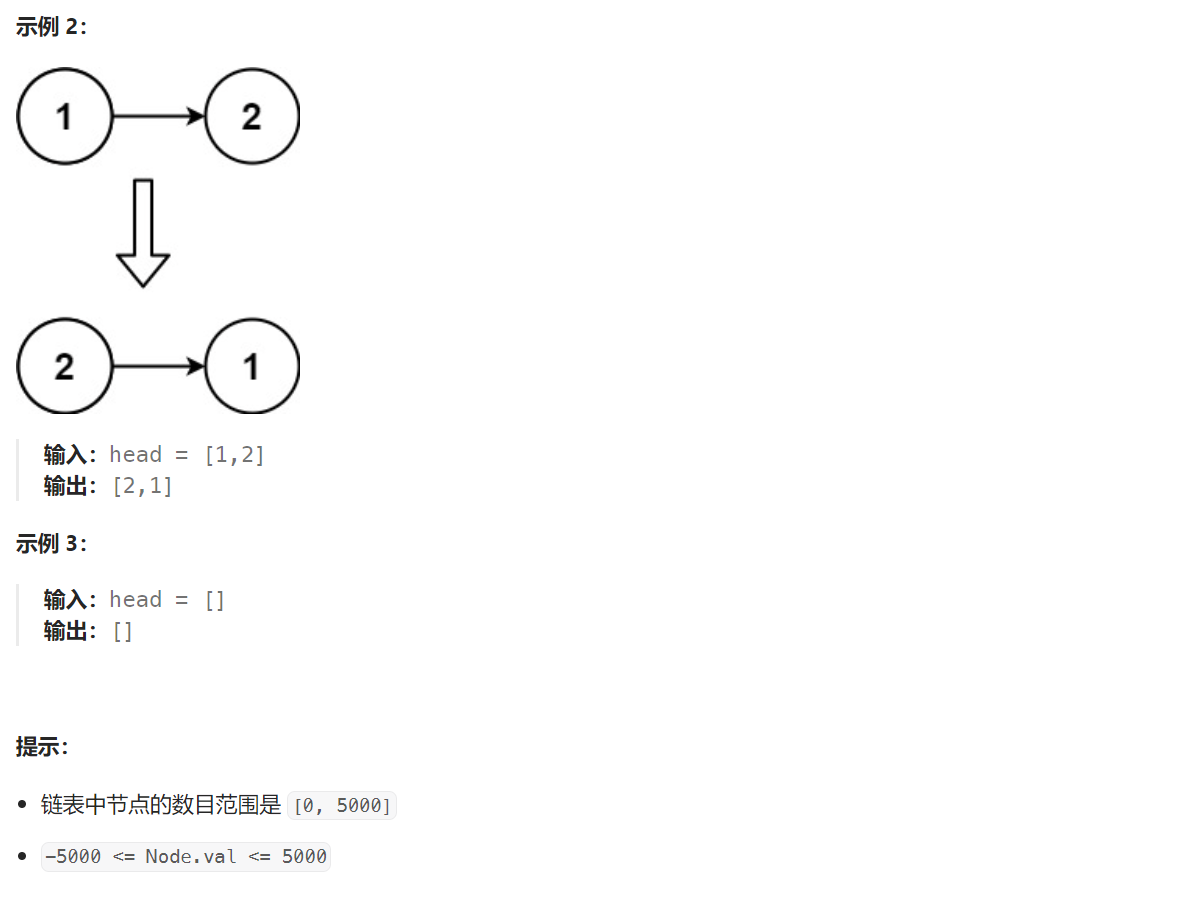
题目解析:题目给定一个单链表,要求我们将其翻转之后返回。
合并链表我们使用的操作是尾插,而反转链表我们则需要用到头插,我们首先拿原始的链表头节点当作头节点,然后再将下一个节点头插到当前头节点就行了。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
return dfs(head);
}
ListNode* dfs(ListNode* head){
if(head == nullptr || head->next == nullptr) return head;
auto next = head->next; //保存剩余的链表
auto res = dfs(next); //保存反转之后的头节点用于返回
next->next = head; //头插
head->next = nullptr;//尾插的时候我们会把所有的head当成最后一个节点,如果不是最后一个节点,那么再递归回去之后的上一层函数会修改next进行正常链接
return res;
}
};
4 两两交换链表中的节点
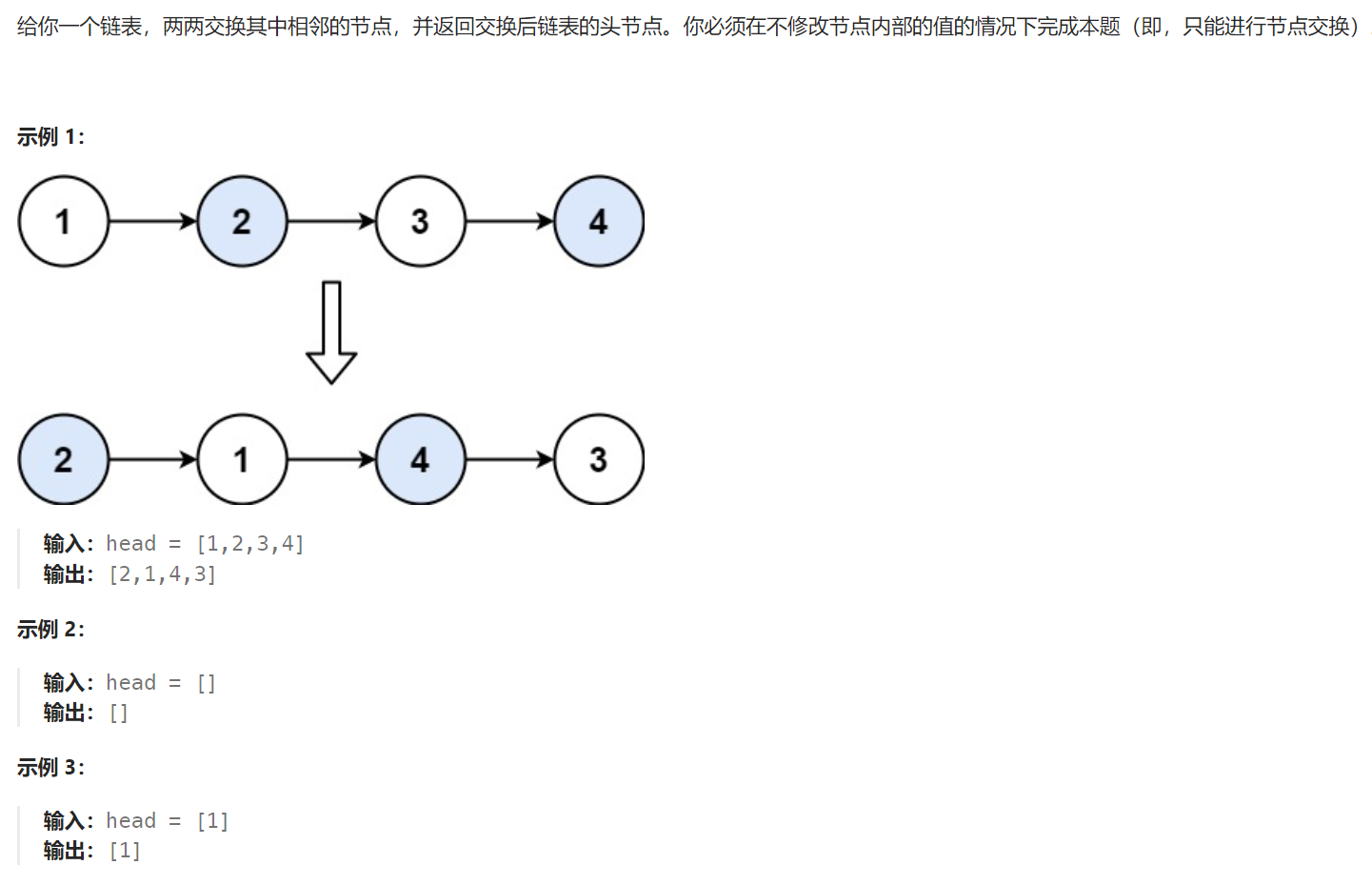
题目解析:给定一个单链表,要求我们将链表的两两节点看成一组,交换每一组的两个节点之后返回。
那么我们就按照题目的意思,两两节点划分为一组来进行交换,如果当前组不满两个节点那么直接返回。
而仅仅俩俩翻转的话,我们总体的思路还是一个尾插,当交换完本组的两个节点之后,剩余的链表进行交换完之后会返回一个头节点,我们只需要将该头节点尾插到当前组的后面就行了。
代码如下:
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
return dfs(head);
}
ListNode* dfs(ListNode* head){
ListNode* n1 = head;
if(!n1) return head;
ListNode* n2 = head->next;
if(!n2) return head;
ListNode* next = n2->next;
//交换n1和n2的顺序
n2->next = n1;
n1->next = dfs(next);
return n2;
}
};
5 Pow(x, n)

题目解析:题目要求我们计算x的n次幂。
本题其实考察的是我们的快速幂算法,对于 x^n ,如果n为偶数,那么我们可以进行转换 x^n=(x^n/2)^2 ,比如 x^4 = (x^2)^2 = ((x^1)^2)^2。
如果n为奇数,那么我们可以先拿一个x出来,剩下的n就是偶数了,比如 x^5 = x^4*x = (((x^1)^2)^2)*x,这样一来,我们对于大指数的幂运算就能很快得出结果。如果暴力运算的话,我们需要计算n次,但是使用快速幂的技巧,我们的运算次数减少到了log(n)。
代码如下:
class Solution {
public:
double myPow(double x, long long n) {//n有可能是最小的负数,转换为正数会溢出,所以我们直接用long long 来接收
if(x == 0 || x == 1 || n == 1) return x;
if(n < 0){
x = 1/x;
n = -n;
}
return dfs(x,n);
}
double dfs(double x , long long n){
if(n == 0) return 1;
double res = dfs(x,n / 2);
res *= res;
if(n%2) res *= x;
return res;
}
};
二 二叉树的DFS
1 计算布尔二叉树的值

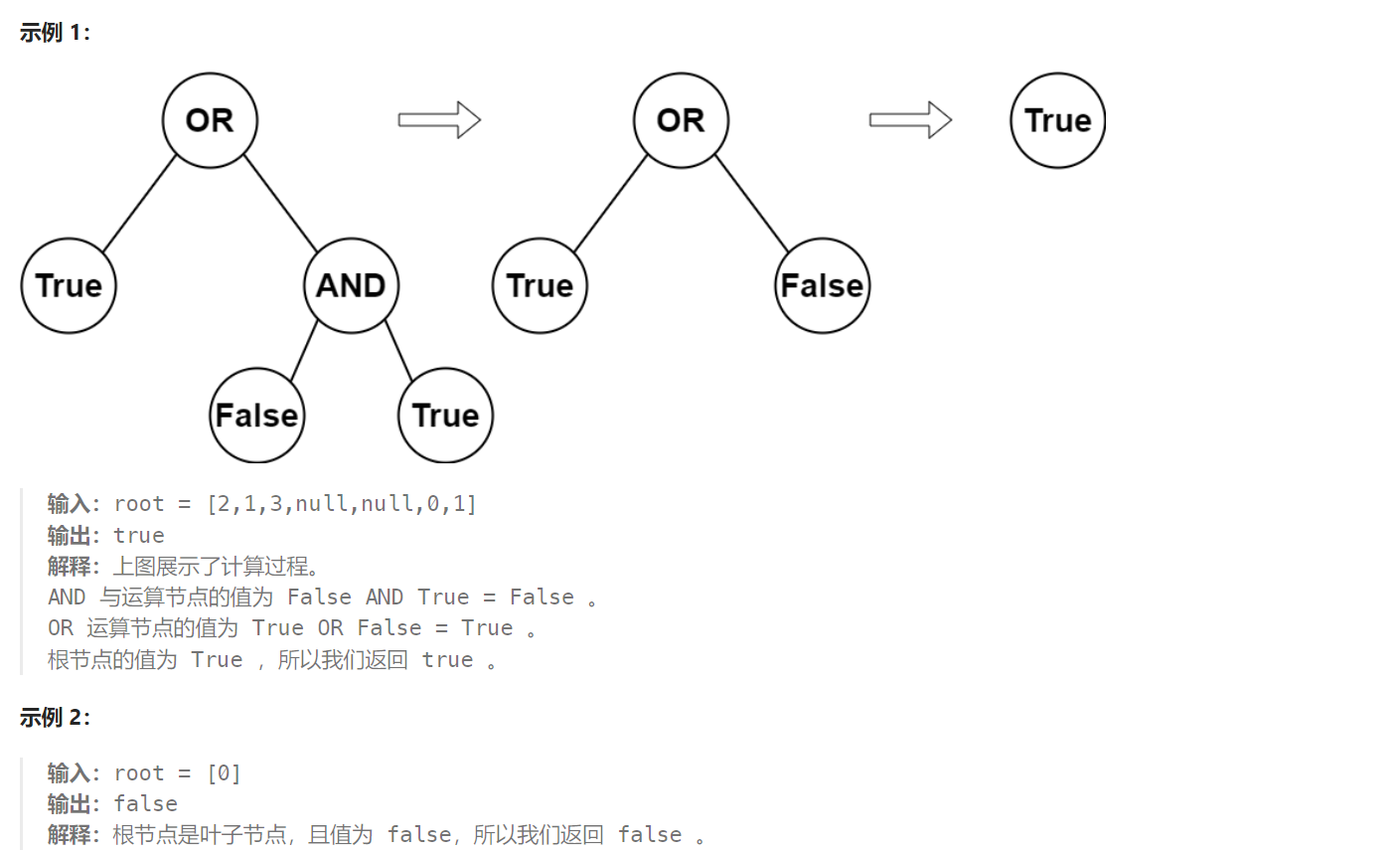
题目解析:给定一棵二叉树,分支节点存储的是运算符,AND和OR,也就是逻辑与和逻辑或,而叶子节点存储的是布尔值,也就是true和false,每一个分支节点的值,就是左右子树的结果进行运算的到的结果,要求我们返回整棵二叉树的结果。
其实本质就是要求我们返回根节点的值,由于要求根节点,我们需要先得到根节点左右子树的结果,那么本质上就是一次二叉树的后序遍历,代码如下。
class Solution {
public:
bool evaluateTree(TreeNode* root) {
if(root->val == 0) return false;
if(root->val == 1) return true;
bool l = evaluateTree(root->left) , r = evaluateTree(root->right);
bool res;
if(root->val == 2) res = l || r;
else res = l && r;
return res;
}
};
2 求根节点到叶节点数字之和
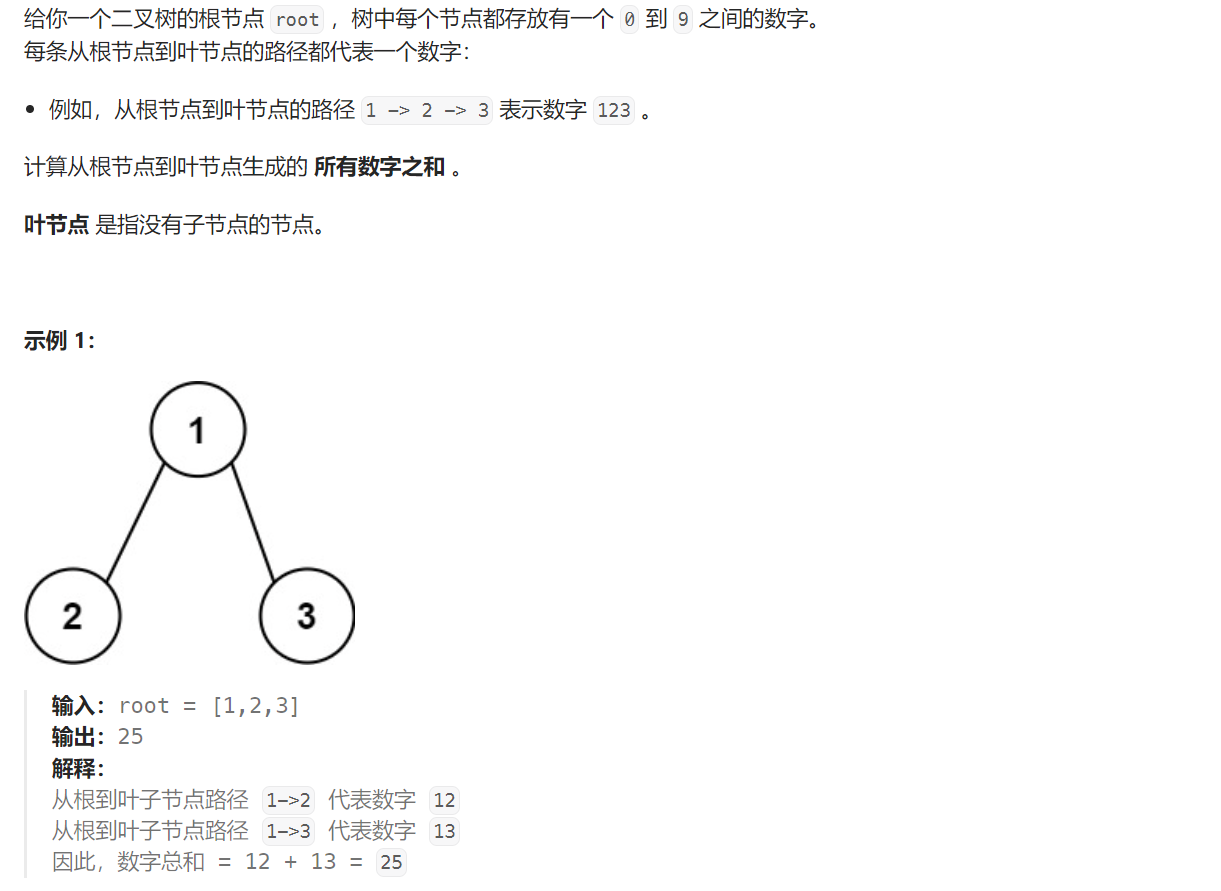
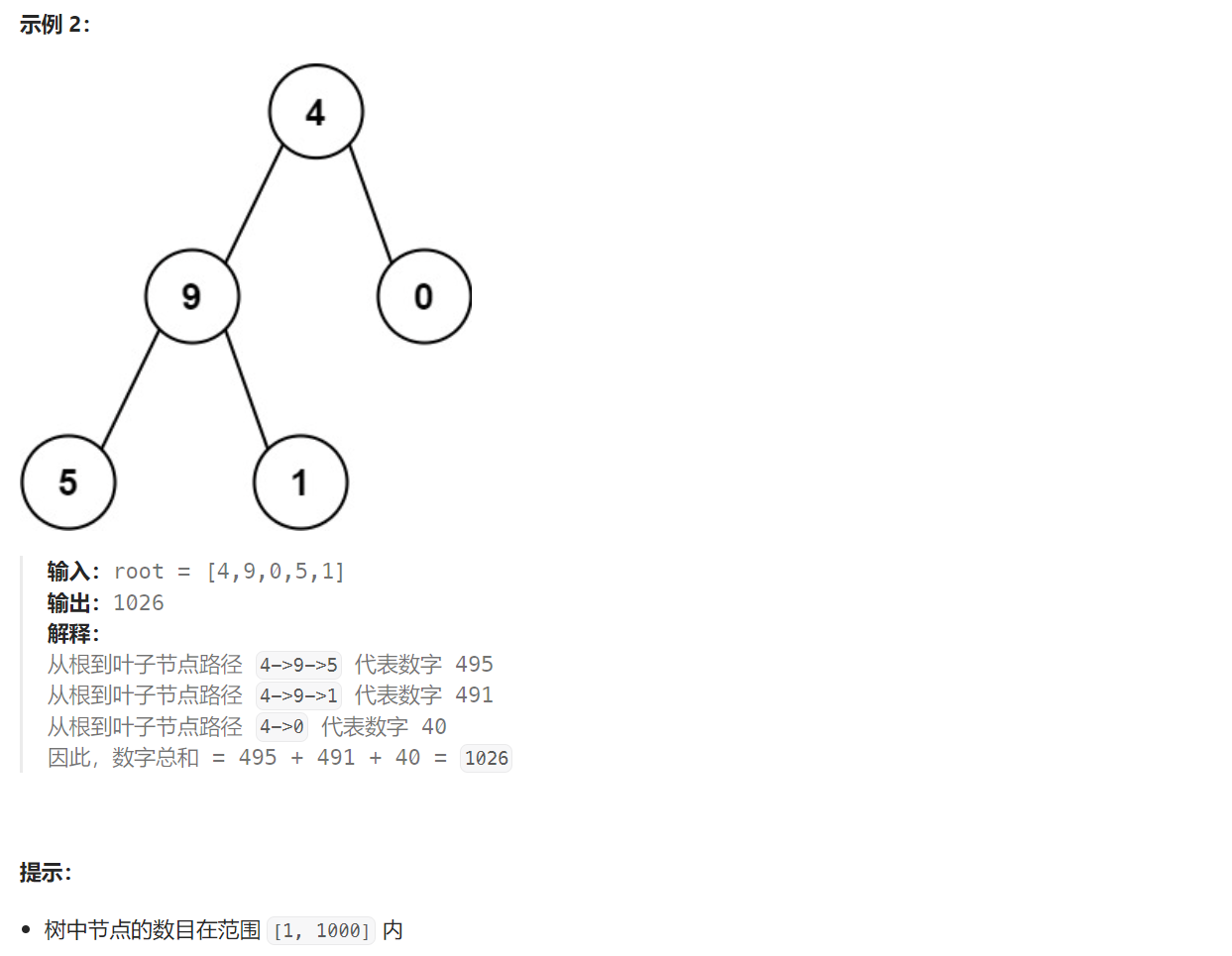
题目解析:本题给定一棵二叉树,每个节点上都有一个0~9的数字,每一条路径的值就是从根节点到叶子节点组成的数字,我们需要求出所有路径的值之和。
那么我们只需要对二叉树做一次dfs或者bfs就能在叶子节点得出所有路径的值,然后累加起来就能得到结果,代码如下:
class Solution {
public:
int res = 0;
int sumNumbers(TreeNode* root) {
if(root) dfs(root,0);
return res;
}
void dfs(TreeNode* root , int prev){ //prev表示父节点的值
int x = prev * 10 + root->val; //本节点的值
if(!root->left && !root->right){ //叶子节点
res += x;
return;
}
if(root->left) dfs(root->left,x);
if(root->right) dfs(root->right,x);
}
};
3 二叉树剪枝
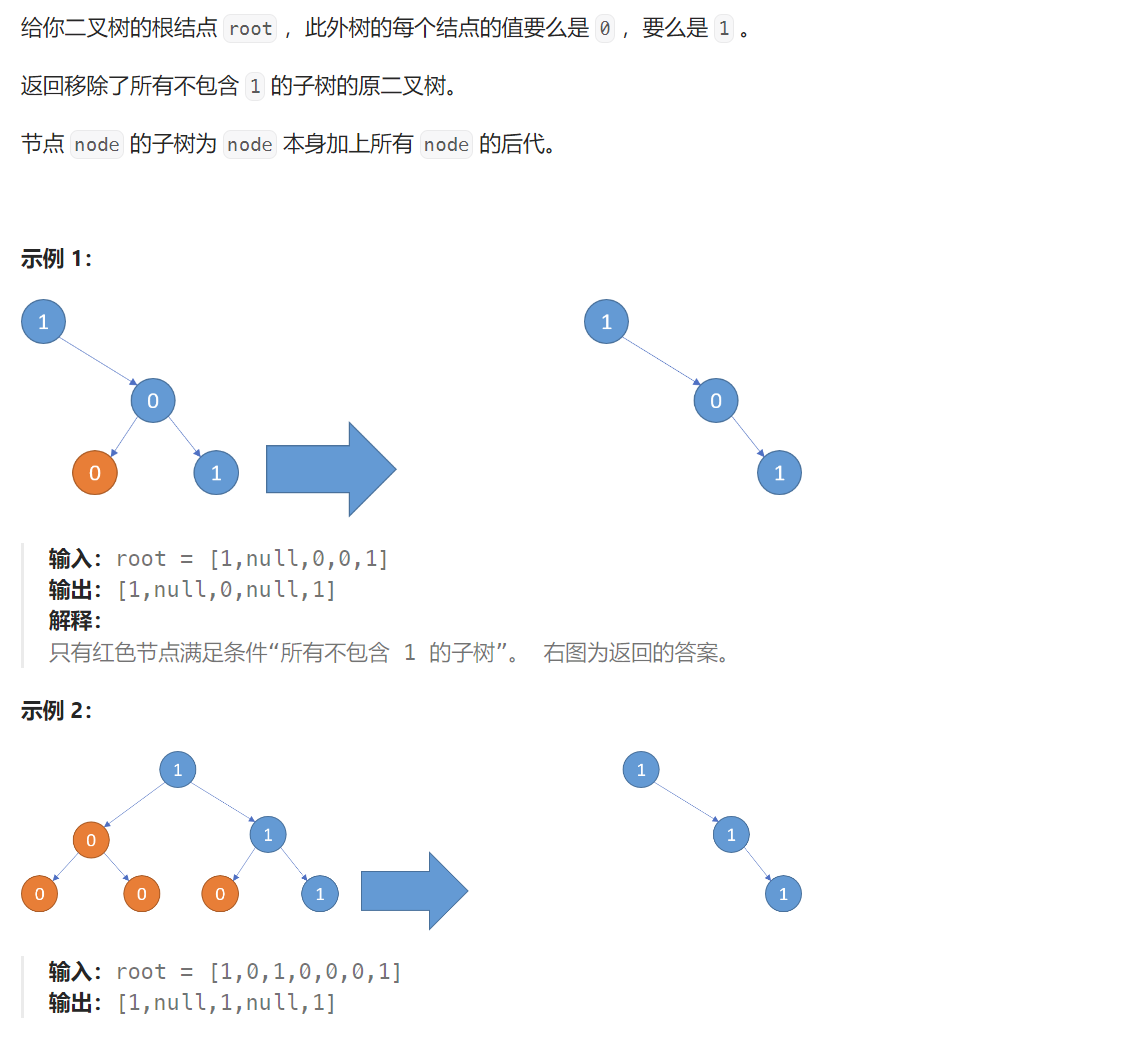
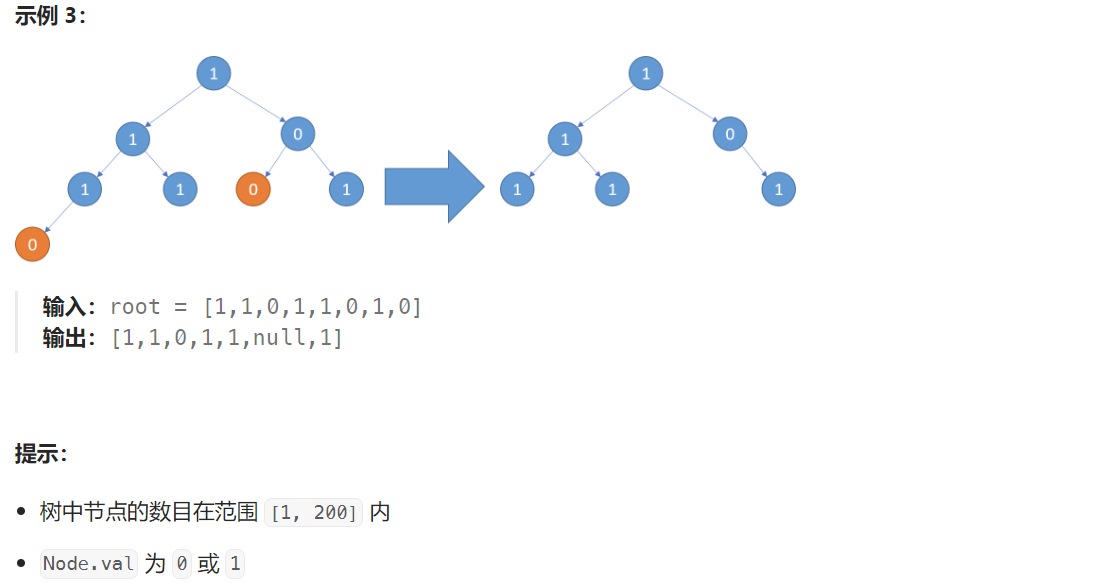
题目解析:给定一棵只包含0和1的二叉树,要求我们删除所有不包含1的子树。
那么对于一个节点,如果左子树全为0,我们需要删除左子树,如果右子树全为0,我们需要删除右子树,如果左右子树全为0,那么还需要返回给上一层,用于删除本节点。
代码如下:
class Solution {
public:
TreeNode* pruneTree(TreeNode* root) {
if(!dfs(root)){ //整棵二叉树都是0
// delete root;
root = nullptr;
}
return root;
}
bool dfs(TreeNode* root){
bool res = false;
if(root->val == 1) res = true;
if(root->left){
bool l = dfs(root->left);
if(!l){
// delete root->left; //删除左子树,此时左子树只剩左子节点
root->left = nullptr;
}
res = res || l;
}
if(root->right){
bool r = dfs(root->right);
if(!r){
// delete root->right; //删除右子树,此时右子树只剩右子节点
root->right = nullptr;
}
res = res || r;
}
return res;
}
};
注意本题我们不要delete删除节点,在整棵树全为0的时候会报错,可能是因为测试用例的root是栈空间的节点。
4 验证二叉搜索树
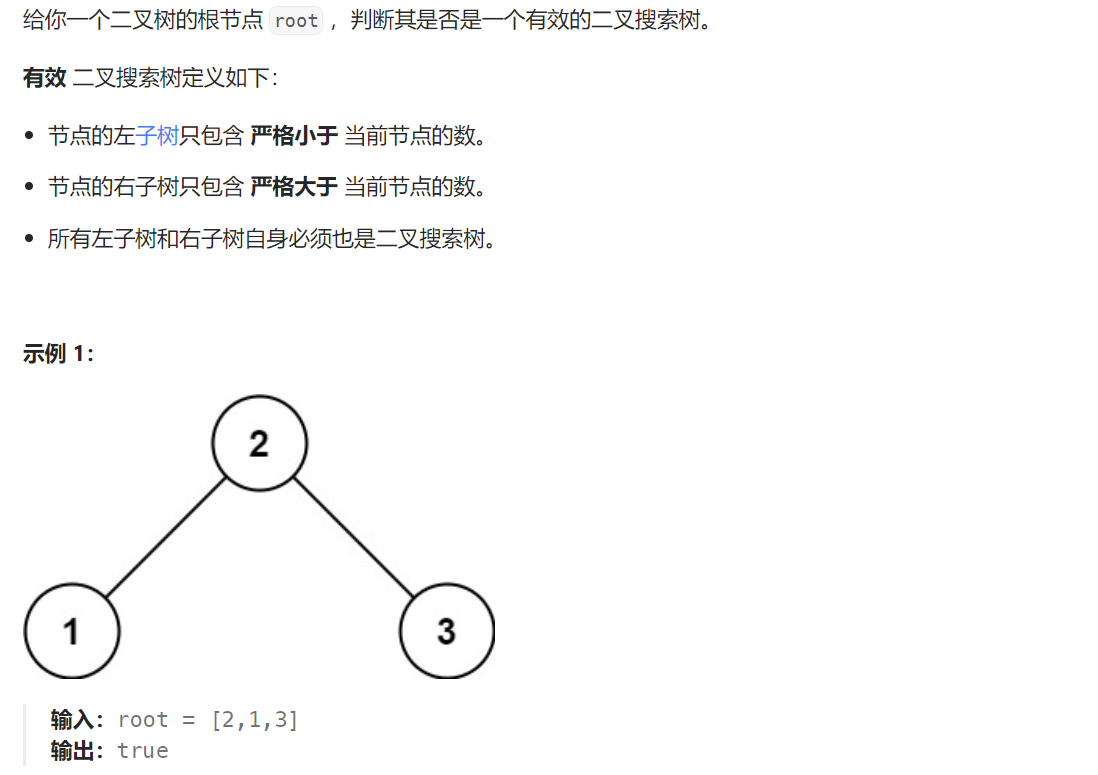

题目解析:给定一棵二叉树,要求我们验证是不是一颗搜索二叉树。搜索二叉树满足左子树小于根,右子树大于根。
根据二叉搜索树的性质,中序遍历有序,我们可以对该二叉树进行一次前序遍历,按顺序记录所有的值,最后判断一下是否有序就行了,但是这样的话会有O(N)的空间复杂度,确保前序遍历的有序性其实我们只需要保证任意一个节点和她的上一个节点的有序性就行了。
我们可以使用一个全局变量记录上一个访问的节点的值。
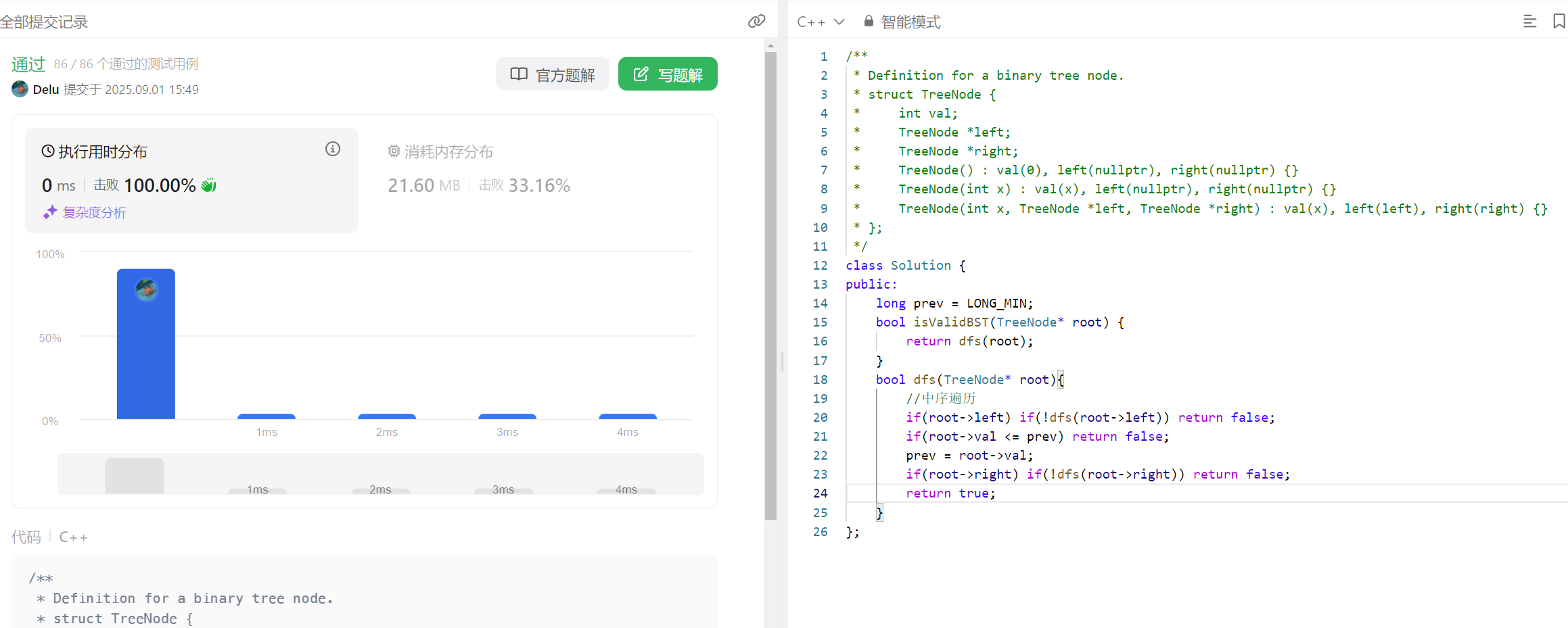
代码如下:
class Solution {
public:
long prev = LONG_MIN;
bool isValidBST(TreeNode* root) {
return dfs(root);
}
bool dfs(TreeNode* root){
//中序遍历
if(root->left) if(!dfs(root->left)) return false;
if(root->val <= prev) return false;
prev = root->val;
if(root->right) if(!dfs(root->right)) return false;
return true;
}
};
5 二叉搜索树中第 K 小的元素
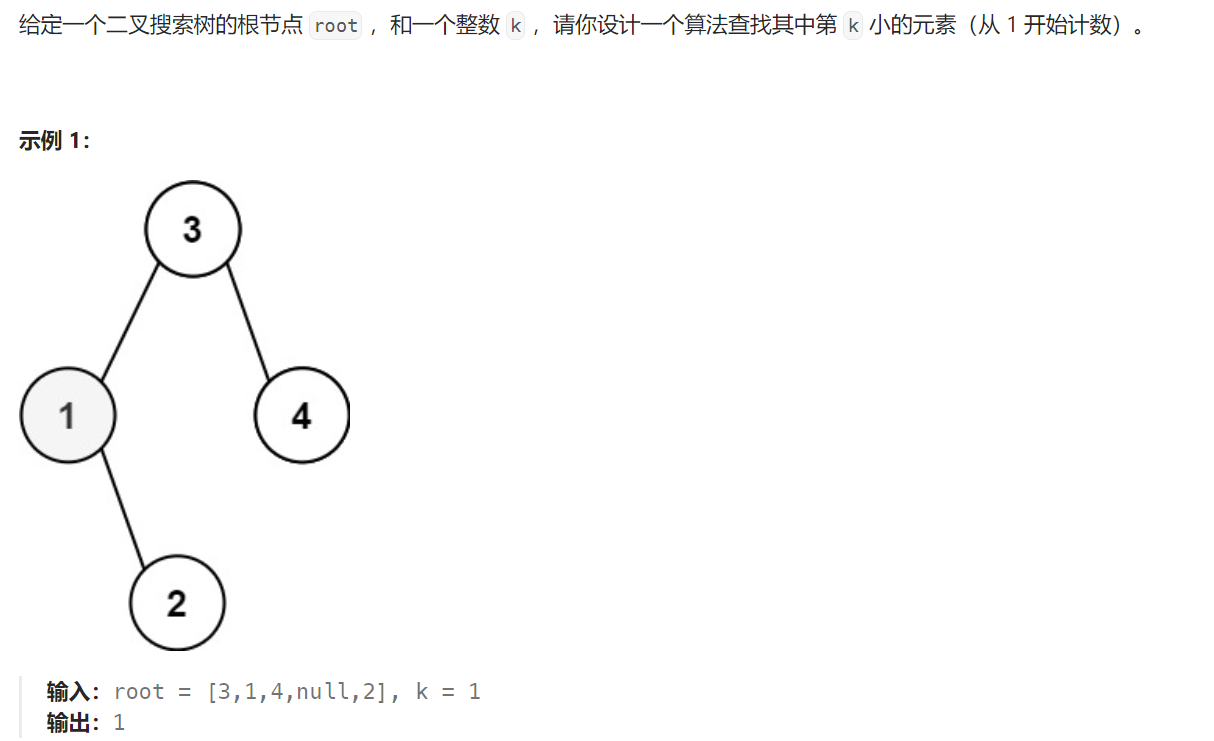
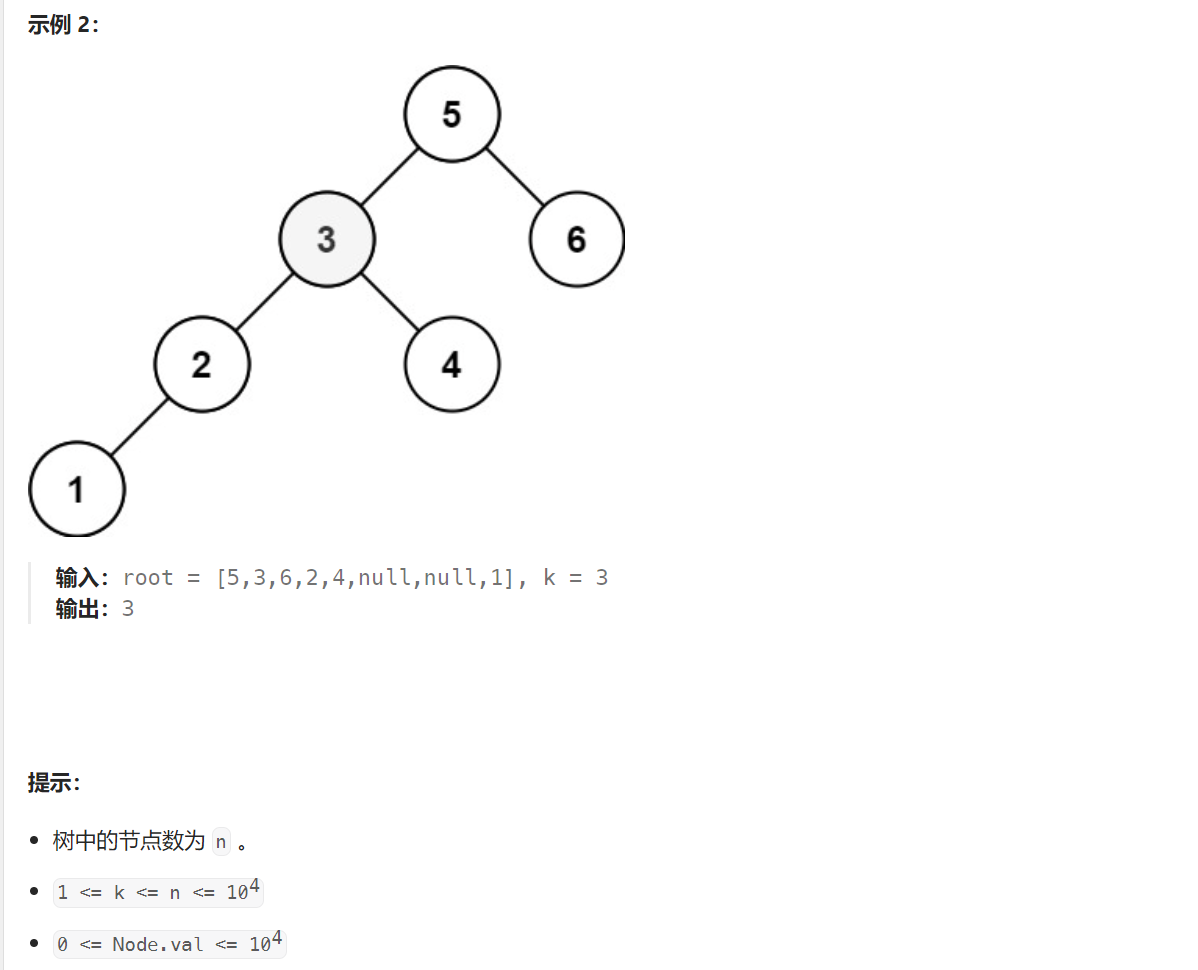
题目解析:本题给定一棵搜索二叉树,让我们返回第k小的元素。
那么我们可以利用搜索二叉树中序遍历有序的特点,中序遍历到第k个节点返回就行了。
代码如下:
class Solution {
public:
int n,res;
int kthSmallest(TreeNode* root, int k) {
n = k;
return dfs(root);
}
int dfs(TreeNode* root){
if(!root || n ==0) return res;
dfs(root->left);
n--;
if(n == 0) res = root->val;
dfs(root->right);
return res;
}
};
三 回溯
回溯其实是在DFS的基础上,做了一些额外的工作比如恢复现场。有些变量我们为了节省空间或者使逻辑更加简单,我们会以引用或者指针形式或者通过全局变量,被所有递归的栈帧共享,就比如我们上面的二.2,我们可以使用全局变量来记录当前节点的值,然后在子节点结束返回之后,将当前节点的x/10 ,将x恢复成父节点的值,以便父节点继续进行递归右子节点或者返回。
1 二叉树的所有路径
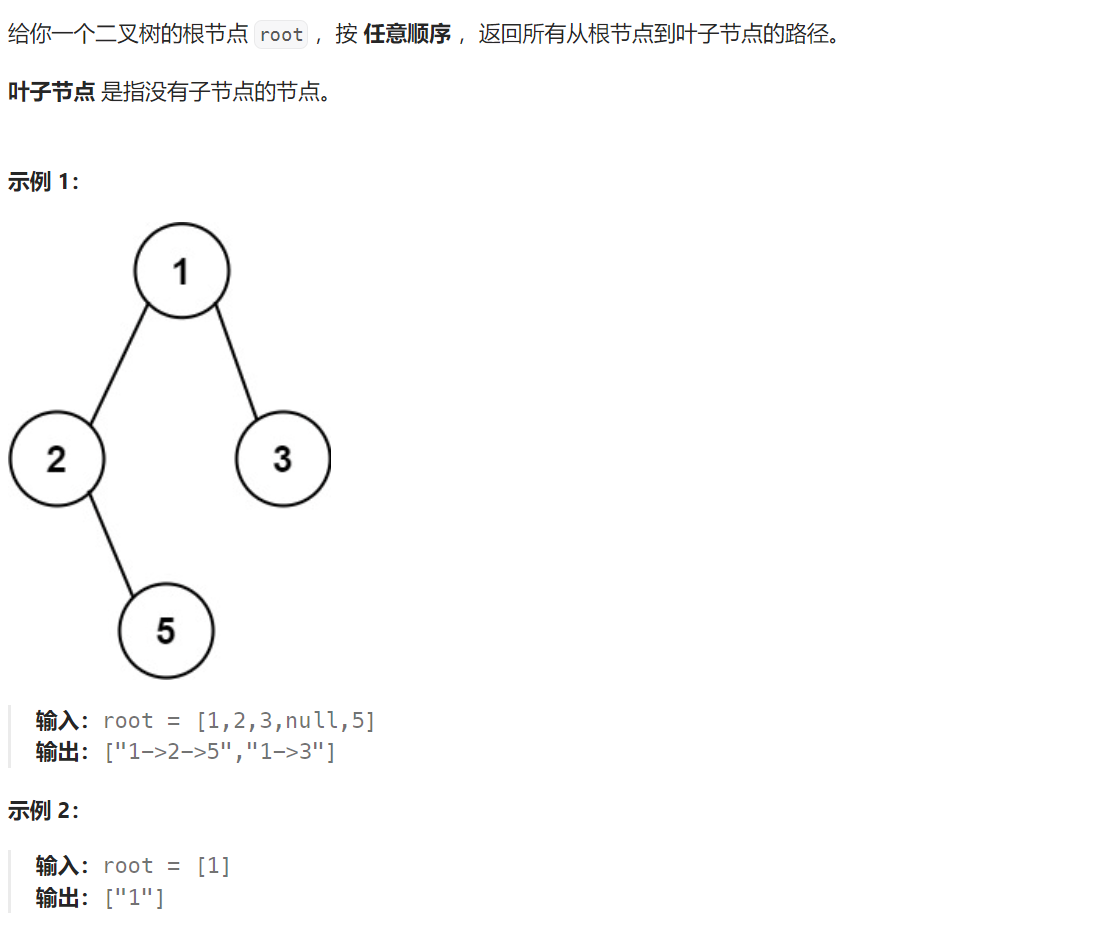
题目解析:给定一棵二叉树,要求我们返回从根节点到所有叶子节点的路径字符串。
本题如果使用常规的递归写法,那么可以写出这样的代码:
class Solution {
public:
vector<string> res;
vector<string> binaryTreePaths(TreeNode* root) {
string str;
dfs(root,str);
return res;
}
void dfs(TreeNode* root , string str){
if(!root) return;
str += to_string(root->val);
str += "->";
if(root->left) dfs(root->left,str);
if(root->right) dfs(root->right,str);
if(!root->left && !root->right){
str.pop_back();
str.pop_back();
res.push_back(str);
}
}
};虽然这样也能解决问题,但是我们能够发现,递归函数传参的时候每一次都是传值传参,每一次都伴随着string的深拷贝,效率其实并不高,那么我们能不能通过引用来进行st的r传参呢?当然能,但是有一个问题就是如果使用引用传参,下一层栈帧可能会修改str的值,这时候可能会出现问题。
也就是在有些递归的栈帧中会对这个共享的str进行修改,那么其实只要我们在函数返回之前,将str还原成函数刚调用的时候,那么就可以了,这就是一种恢复现场,代码如下:
class Solution {
public:
vector<string> res;
vector<string> binaryTreePaths(TreeNode* root) {
string str;
dfs(root,str);
return res;
}
void dfs(TreeNode* root , string& str){
if(!root) return;
int n = str.size();
str += to_string(root->val);
str += "->";
if(root->left) dfs(root->left,str);
if(root->right) dfs(root->right,str);
if(!root->left && !root->right){
//这里的pop_back 是为了将最后面的 -> 删除
str.pop_back();
str.pop_back();
res.push_back(str);
}
str.resize(n); //返回之前还原
}
};当然,由于str是全局共享的,我们搞成全局变量更好,这样能省去传参的开销,代码如下:
class Solution {
public:
string str;
vector<string> res;
vector<string> binaryTreePaths(TreeNode* root) {
dfs(root);
return res;
}
void dfs(TreeNode* root ){
if(!root) return;
int n = str.size();
str += to_string(root->val);
str += "->";
if(root->left) dfs(root->left);
if(root->right) dfs(root->right);
if(!root->left && !root->right){
//这里的pop_back 是为了将最后面的 -> 删除
str.pop_back();
str.pop_back();
res.push_back(str);
}
str.resize(n); //返回之前还原
}
};
2 全排列

题目解析:本题给定一个不含重复元素的数组,要求我们返回这些元素的全排列,排列的顺序没有要求。
对于全排列系列的问题,最关键的就是要做到不重不漏,也就是不能出现重复的序列,也不能漏掉某个序列。
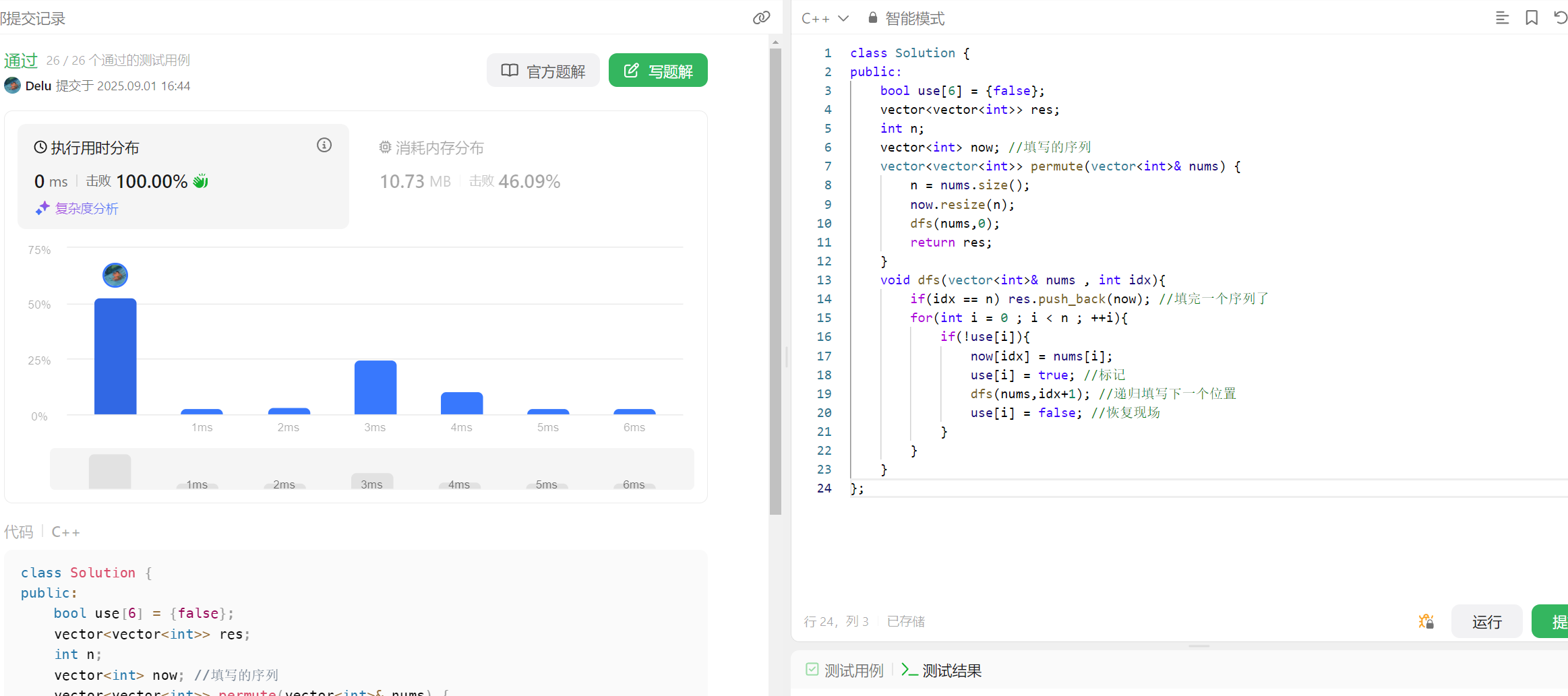
同时,做这类题有一个技巧,由于排列的大小和原数组的大小是一样的,那么我们的全排列的递归过程就可以看作是在 n 个空位上进行选数填写,画出决策树,如下:
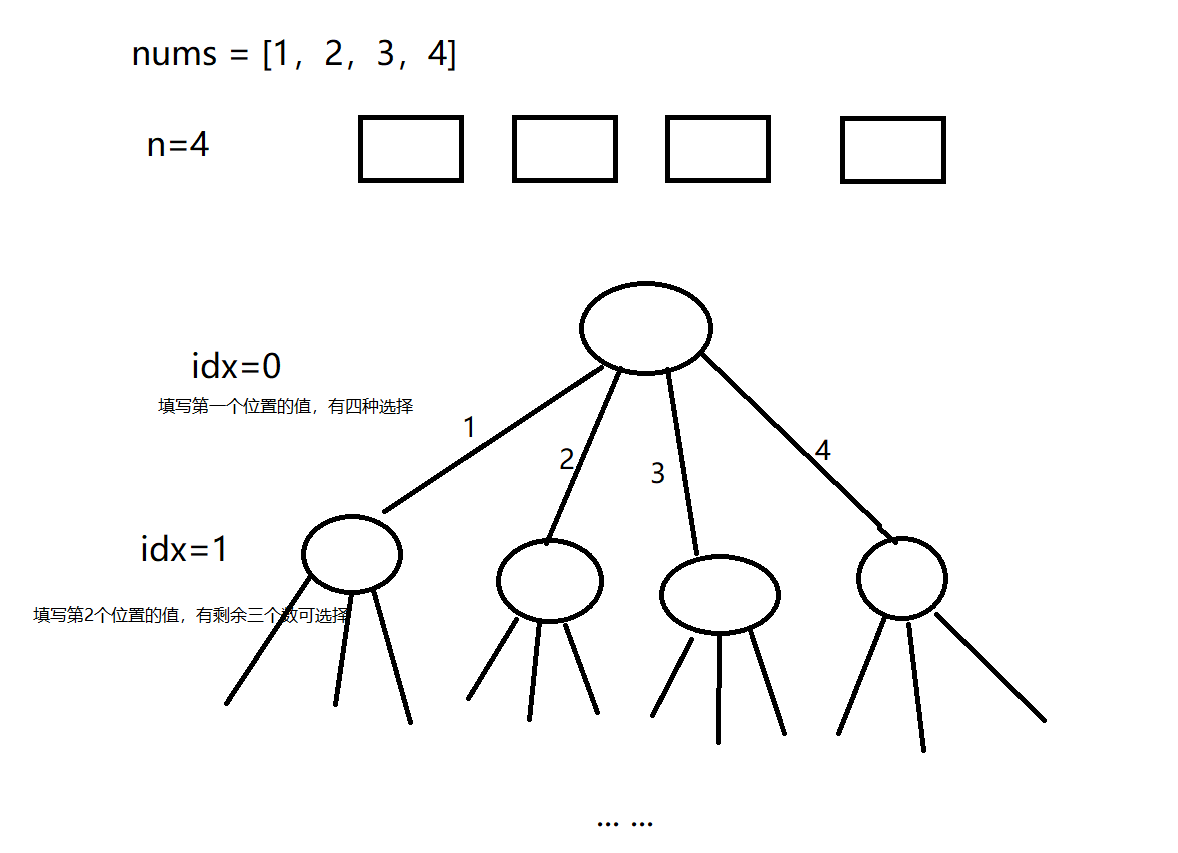
其实决策树的第i层填写的就是排列的下标i的位置,对于第一个位置我们有n个数可选,但是选完之后,我们需要递归到第2层,第2层只有n-1个数可选,那么具体是哪n-1个数,我们是需要一个bool数组来标记哪些元素使用过,哪些元素未使用的。
代码如下:
class Solution {
public:
bool use[6] = {false};
vector<vector<int>> res;
int n;
vector<int> now; //填写的序列
vector<vector<int>> permute(vector<int>& nums) {
n = nums.size();
now.resize(n);
dfs(nums,0);
return res;
}
void dfs(vector<int>& nums , int idx){
if(idx == n) res.push_back(now); //填完一个序列了
for(int i = 0 ; i < n ; ++i){
if(!use[i]){
now[idx] = nums[i];
use[i] = true; //标记
dfs(nums,idx+1); //递归填写下一个位置
use[i] = false; //恢复现场
}
}
}
};
2 全排列 II

题目解析:本题依旧是返回全排列,但是给定元素可能会出现重复元素,但是我们返回的全排列中不能出现重复的全排列。
还是一样,全排列问题最重要的就是不重不漏,不漏其实很好解决,因为我们dfs过程中,枚举idx位置填的元素的时候会将所有未被选过的元素都填一遍,那么一定不会漏。在本题中给定的原始元素会出现重复元素,那么如果还是按照上面的做法,就会出现重复的全排列,比如我们给定[1,2,3,1],那么我们枚举idx = 0 的时候,两个1都会枚举到,[1,_,_,_] , [2,_,_,_].[3,_,_,_],[1_,_,_]
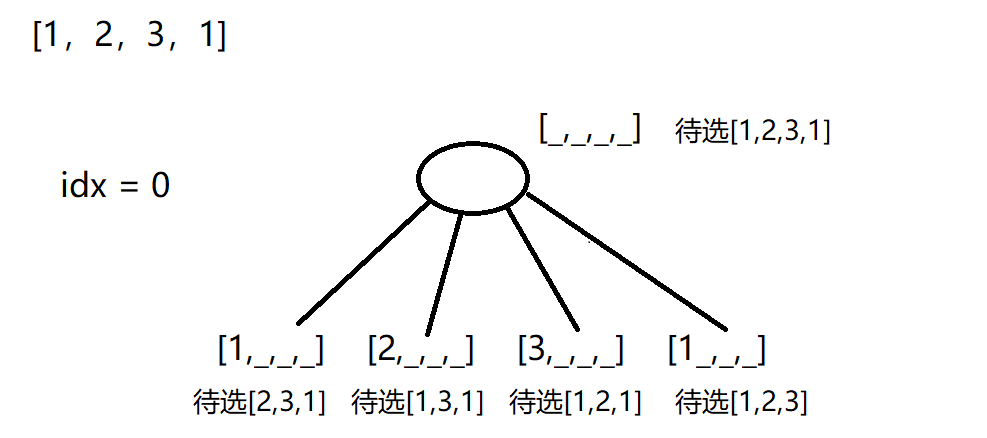
那么后续每一个分支一定会枚举出重复的排列。
我们如何避免呢?就拿idx=0来举例,当我们已经枚举过 now[idx] = 1 ,那么后续再遇到1的时候,我们直接跳过,不再继续枚举1,而是去枚举其他的数,换句话说,在每一层dfs/每一个位置中,相同的数我们只填一遍。这样一来我们上面的决策树就可以变成这样:
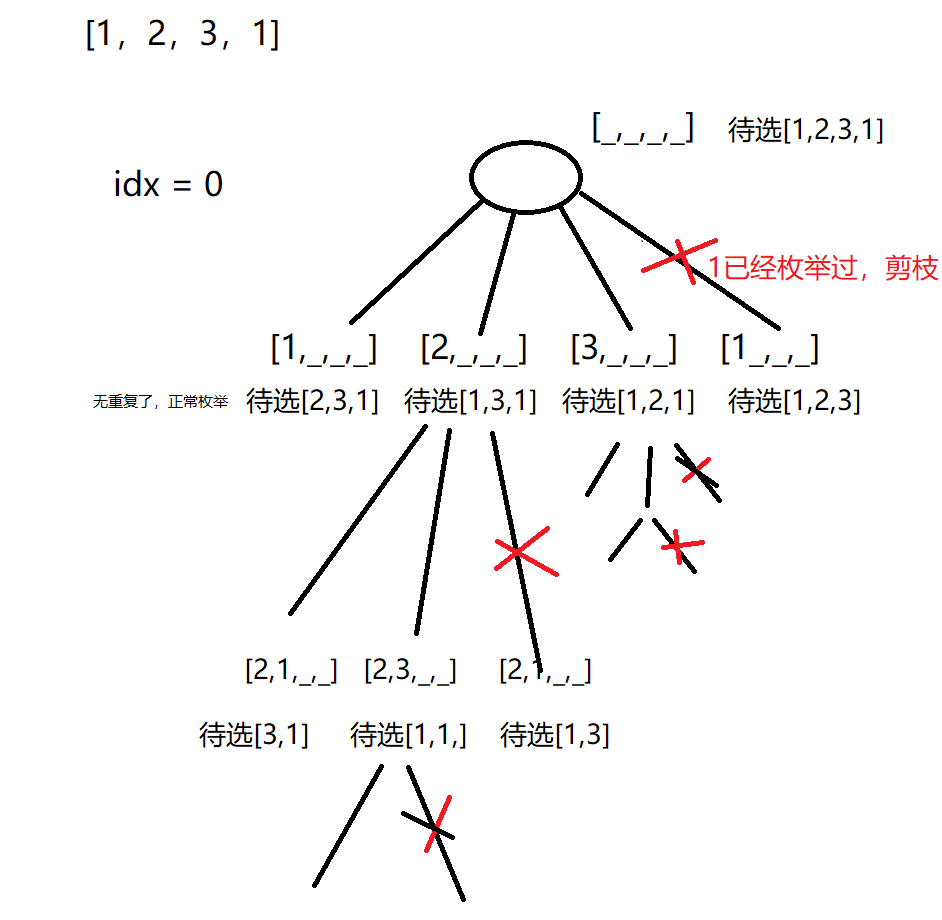
这样一来,我们会将所有的会出现重复排列的分支都进行剪枝。
那么如何在每一层中都只枚举一次相同的数呢? 我们可以在dfs之前先对数据进行预处理,进行排序,这样一来相同的数就相邻了,而我们在枚举选数的时候是从前往后遍历的,当我们枚举到nums[i]的时候,发现 nums[i-1] == nums[i] 且 nums[i-1]没有被使用过,标记为false,那么说明nums[i-1]在上层未被选择,但是在本层dfs枚举的时候,已经枚举过idx位置填nums[i-1]了,不过是后续恢复现场了,所以我们不会继续选择nums[i]。 同理后续不管有多少连续相同的,都不会再填在idx位置。 为什么这样能判断呢? 因为我们在所有位置枚举选数的时候,都是从前往后遍历的,那么对于多个相同的数,使用的时候也一定是从前往后使用的,换句话说,如果[i,j]区间相同,那么在某一层dfs,如果我们使用了该数,那么他一定是使用了一个连续区间[i,x] x<=j,而 [x+1,j]一定全未使用过。
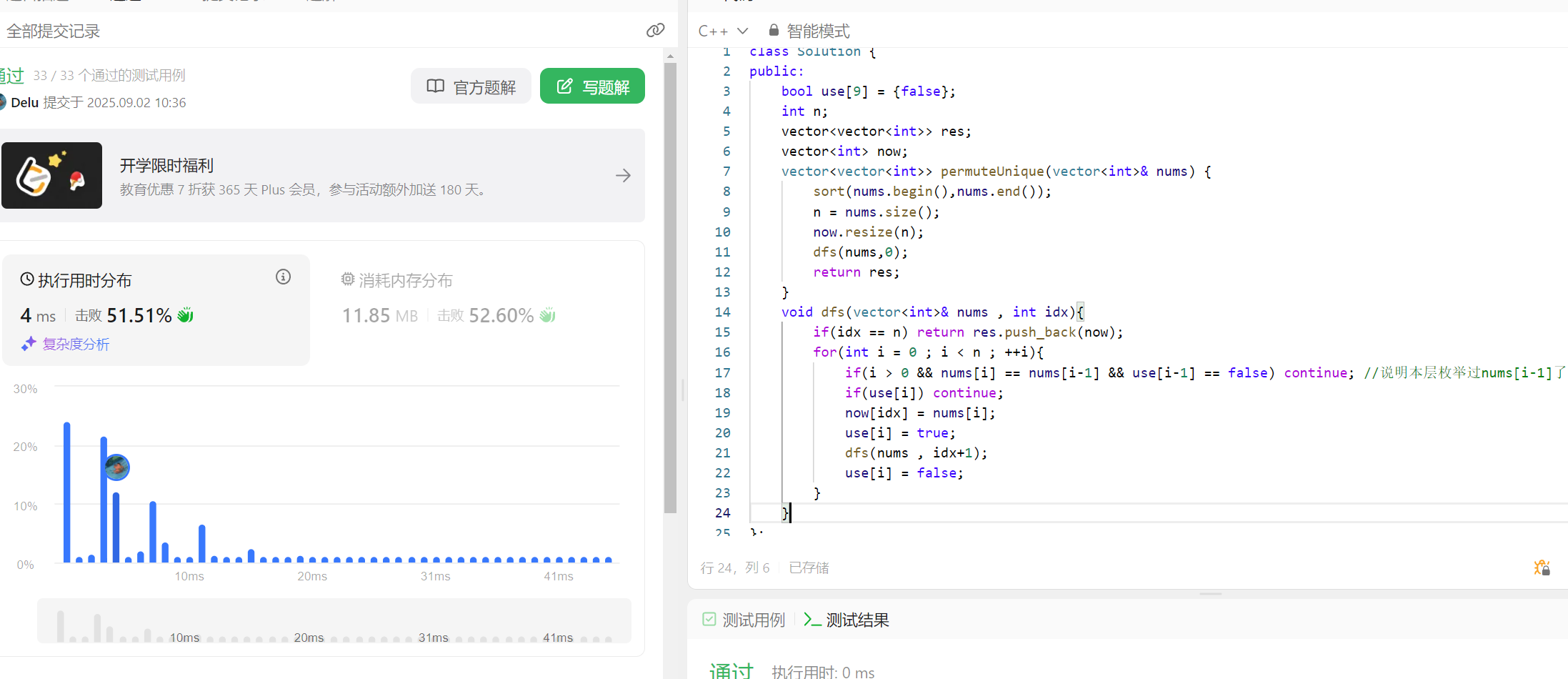
代码如下:
class Solution {
public:
bool use[9] = {false};
int n;
vector<vector<int>> res;
vector<int> now;
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(),nums.end());
n = nums.size();
now.resize(n);
dfs(nums,0);
return res;
}
void dfs(vector<int>& nums , int idx){
if(idx == n) return res.push_back(now);
for(int i = 0 ; i < n ; ++i){
if(i > 0 && nums[i] == nums[i-1] && use[i-1] == false) continue; //说明本层枚举过nums[i-1]了
if(use[i]) continue;
now[idx] = nums[i];
use[i] = true;
dfs(nums , idx+1);
use[i] = false;
}
}
};
3 子集

题目解析:本题要求返回数组nums的所有子集。子集与内部元素顺序无关,我们不能返回重复的子集,比如[1,2]和[2,1]本质是同一个子集。
其实本题也很简单,由于子集与顺序无关,为了避免重复子集,我们一般这样做,每一次选择划定好一个边界,下一次选数的时候从该边界往后选。比如我们选的最后一个位置是 x ,那么后续子集选下一个数的时候,我们从[x,n)中选,而不会去[0,x]中选了。
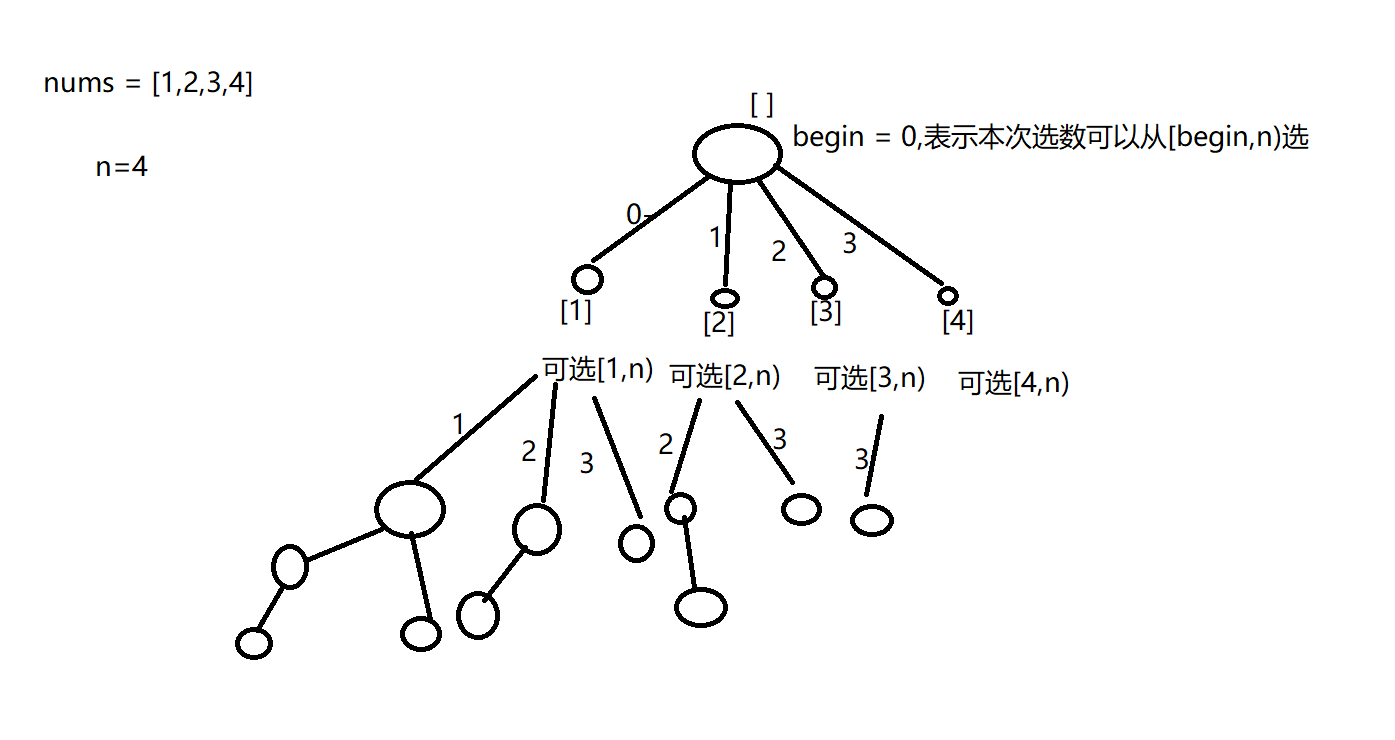
这一棵决策树画下来,我们需要的子集在哪里呢?树上所有的节点都是我们需要的子集,那么我们可以在每一层dfs进去之后就统计一下结果。
代码如下:
class Solution {
public:
vector<vector<int>> res;
vector<int> now;
int n;
vector<vector<int>> subsets(vector<int>& nums) {
n = nums.size();
now.reserve(n);
dfs(nums,0);
return res;
}
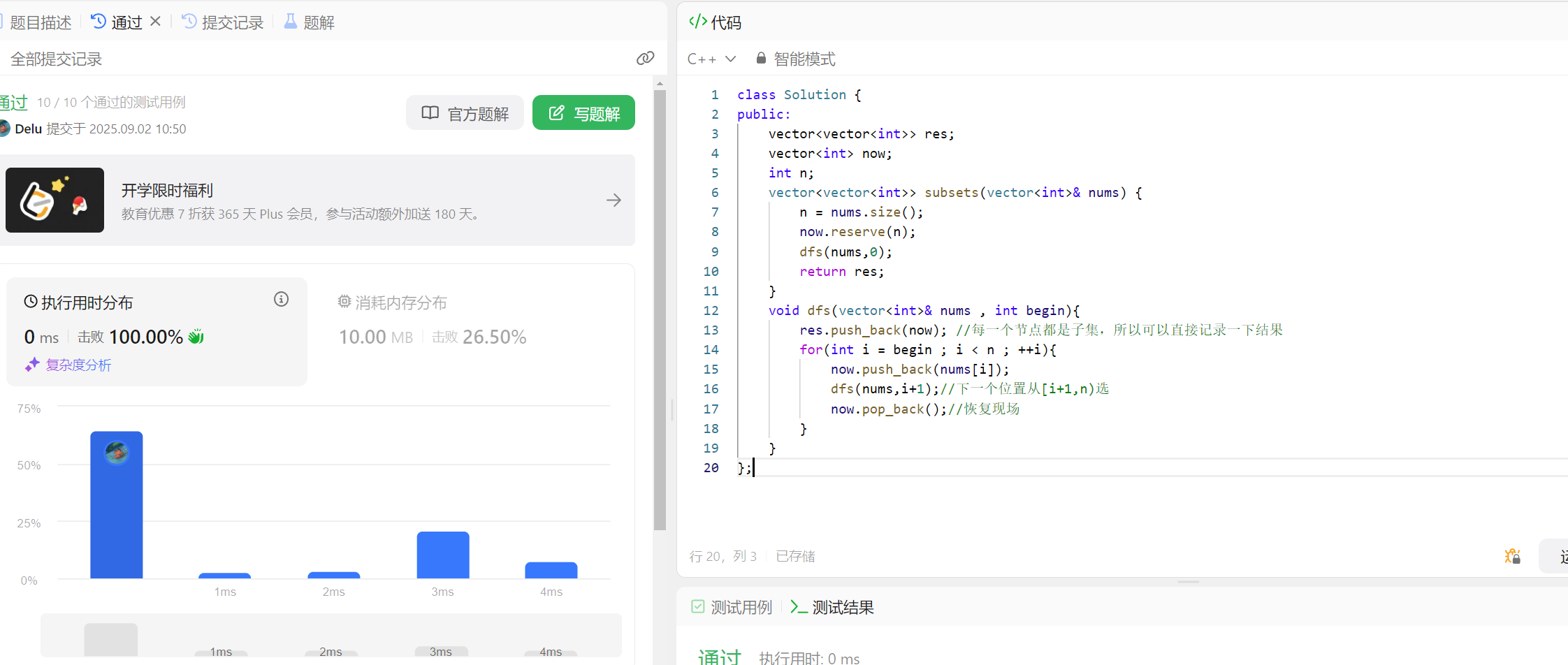
void dfs(vector<int>& nums , int begin){
res.push_back(now); //每一个节点都是子集,所以可以直接记录一下结果
for(int i = begin ; i < n ; ++i){
now.push_back(nums[i]);
dfs(nums,i+1);//下一个位置从[i+1,n)选
now.pop_back();//恢复现场
}
}
};
4 找出所有子集的异或总和再求和


题目解析:本题要求我们找出nums的所有子集,然后求出所有子集的元素异或和,最终将所有子集的异或和加起来求和返回。
那么从题目描述来看还是要我们枚举出所有的子集,记录异或和来做,而枚举子集的做法我们参考上一题,由于本题不需要我们返回子集,而是需要返回异或和,那么我们记录的也是异或和,由于异或运算的可逆性,我们也可以很容易恢复现场,代码如下:
class Solution {
public:
int res = 0 ;
int now = 0 ;
int n ;
int subsetXORSum(vector<int>& nums) {
n = nums.size();
dfs(nums,0);
return res;
}
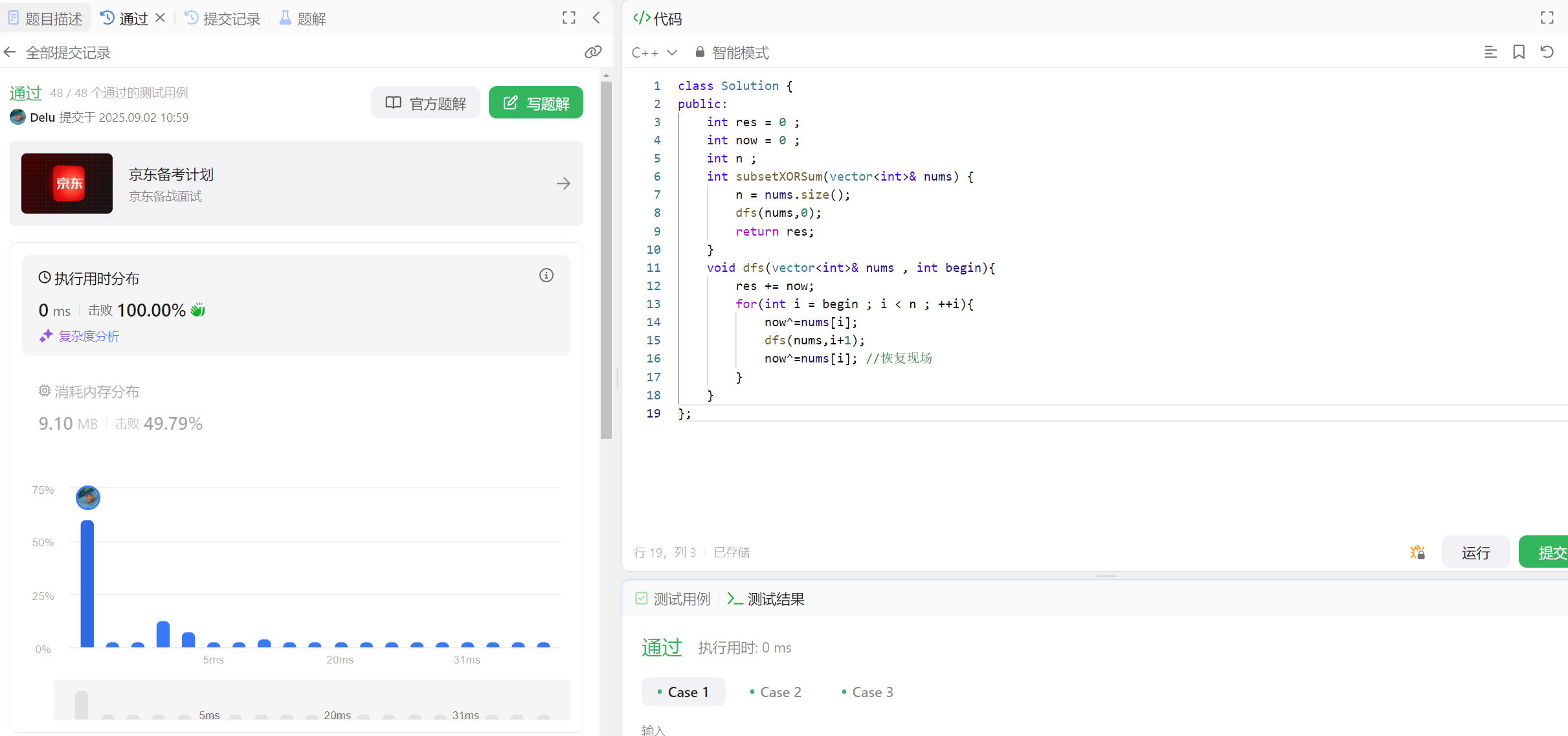
void dfs(vector<int>& nums , int begin){
res += now;
for(int i = begin ; i < n ; ++i){
now^=nums[i];
dfs(nums,i+1);
now^=nums[i]; //恢复现场
}
}
};
5 电话号码的字母组合

题目解析:给定一个数字字符串,每个数字可以映射多个字符,要求我们返回该数字字符串可以映射的所有字符串。
本题就是一个简单的暴力枚举,数字字符串的长度和最终的字符串长度是相等的,同时是一一对应的,我们需要的是枚举每个数字映射的字符,也就是结果字符串的每一个位置的可选字符。
代码如下:
class Solution {
public:
string now;
vector<string> res;
vector<string> strs = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}; //映射表
int n;
vector<string> letterCombinations(string digits) {
n = digits.size();
now.resize(n);
if(n) dfs(digits,0); //注意n==0特殊处理
return res;
}
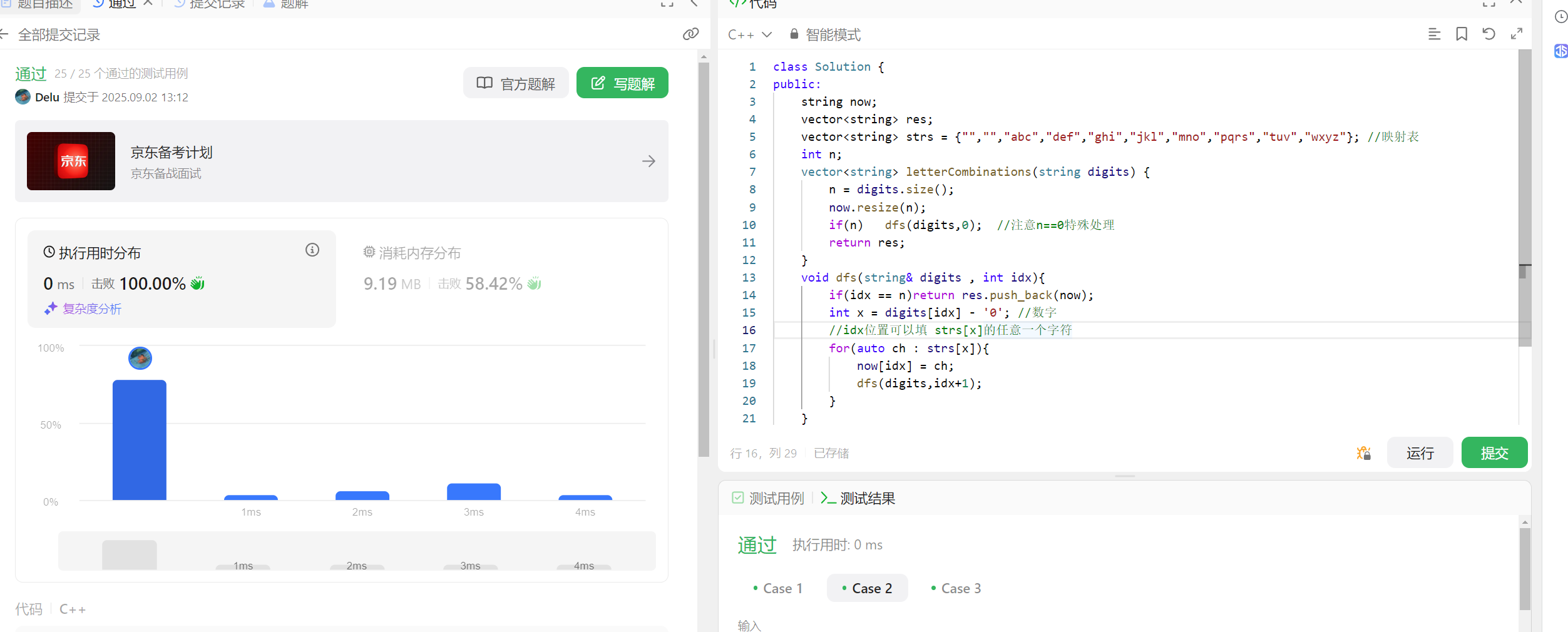
void dfs(string& digits , int idx){
if(idx == n)return res.push_back(now);
int x = digits[idx] - '0'; //数字
//idx位置可以填 strs[x]的任意一个字符
for(auto ch : strs[x]){
now[idx] = ch;
dfs(digits,idx+1);
}
}
};
四 剪枝
剪枝这个词可能听起来很高级,但是在dfs中,剪枝其实就是预先将一些不可能是正确结果的分支排除掉,不去递归这些确定错误的分支。至于何为错误的分支,则需要根据题意或者说具体的场景来确定,我们可以从下面几个题来简单了解如何剪枝。同时在本小节里面的题目并不一定都设计剪枝,更多可能涉及的时回溯,一半回溯和剪枝以及dfs本身就是相互掺杂的,或者说他们本就是在一个大的概念下的一些细分分支。
1 括号生成
题目解析:本题要求生成包含n对括号的有效括号组合。
那么什么是有效括号组合呢?简单来说每一个左括号后面都有能够和他匹配的右括号,在判断一个字符串是否有效括号对的时候,可以从前往后遍历,遍历到任意位置,都必须要保证左括号的数量大于等于右括号的数量,这样就能够快速判断是否为有效括号对。
而本题要求我们构建有效括号对,其实也很简单,我们还是从前往后构建,当我们在填写 idx 位置的时候,我们可以记录前面出现的左括号数量和右括号数量,如果左括号数量小于n,那么idx位置可以填左括号,反之只能填右括号了,如果此时左括号的数量大于右括号的数量,那么idx位置也可以填右括号。
本题的剪枝就体现在当左括号和右括号数量相等时,我们不会去添加右括号,因为添加右括号之后一定是一个不合法的括号组合。
我们使用dfs来模拟这个过程就行了。代码如下:
class Solution {
public:
int lcnt; //左括号数量
int rcnt; //右括号数量
string now;
int n;
vector<string> res;
vector<string> generateParenthesis(int n1) {
n = n1;
now.resize(n*2);
dfs();
return res;
}
void dfs(){
if(rcnt == n) return res.push_back(now);
//1、能否填左括号
if(lcnt < n){
now[lcnt+rcnt] = '(';
lcnt++;
dfs();
lcnt--; //恢复现场
}
//2、能否填右括号
if(lcnt > rcnt){
now[lcnt+rcnt] = ')';
rcnt++;
dfs();
rcnt--;//恢复现场
}
}
};
2 组合

题目解析:题目要求我们返回从[1,n]中选任意k个数的所有组合。
本题其实就是一个基础的类似于全排列的题目,相当于k个位置,我们每一层dfs只选一个位置来填就行了。 但是要注意的是,我们枚举idx位置的时候,必须要为后续的填值留一定余量,也就是除了最后一个位置,其他位置不能直接枚举到n。对于dfs(m,c),表示在[m,n]中找出c个元素的组合。
本题的剪枝体现在我们枚举时,除了最后一个位置可以枚举到n之外,其余位置都不会枚举到n,因为如果枚举到n了,后续剩余的位置就没这么多数可选了。
代码如下:
class Solution {
public:
vector<int> now;
vector<vector<int>> res;
int n;
int k;
vector<vector<int>> combine(int n1, int k1) {
n = n1 , k = k1;
now.reserve(k);
dfs(1);
return res;
}
void dfs(int m){ //在[m,n]找k个数的组合
if(k == 0) return res.push_back(now);
// if(n - m + 1 < k) return; //后面数不够了
for(int i = m ; i <= n - k + 1 ; ++i){
now.push_back(i);
--k;
dfs(i+1);
++k;//恢复现场
now.pop_back();
}
}
};
3 目标和

题目解析:本题给定一个nums数组,要求我们在nums的每个元素前面加上 + 或者 - ,构成一个表达式,表达式的结果为target,有多少个这样的表达式。
那么我们直接暴力枚举,为每一个元素前面加上+或者-就行了。
代码如下:
class Solution {
public:
int sum = 0;
int target;
int n;
int res = 0;
int idx = 0;
int findTargetSumWays(vector<int>& nums, int target1) {
target = target1;
n = nums.size();
dfs(nums);
return res;
}
void dfs(vector<int>& nums){
if(idx == n){
if(sum == target) ++res;
return;
}
//1、 +
sum += nums[idx++];
dfs(nums);
sum -= nums[--idx];
//2、 -
sum -= nums[idx++];
dfs(nums);
sum += nums[--idx];
}
};
当然本题最优的解法还是动态规划,详细可以参考:
4 组合总和

题目解析:给定一个无重复元素的数组,以及一个目标值target,我们需要在数组中找出一些元素的组合(每个元素可以选无限多次),使得组合的总和为target,返回这些所有的组合。
本题其实如果只求组合数量用完全背包是最方便的,但是由于我们需要记录每一个组合,那么使用回溯则更加简洁。我们还是记录一个组合数组以及一个sum,当sum为target或者大于target的时候本条分支就结束了,因为所有元素都是正数,不存在负数。这就是本题的剪枝策略。
代码如下:
class Solution {
public:
int n;
int target;
int sum = 0;
vector<int> now;
vector<vector<int>> res;
vector<vector<int>> combinationSum(vector<int>& candidates, int target1) {
now.reserve(40);
target = target1;
n = candidates.size();
dfs(candidates,0);
return res;
}
void dfs(vector<int>& candidates , int idx){
if(sum > target) return;
if(sum == target) return res.push_back(now);
//否则还需要选数,从[idx,n)选
for(int i = idx ; i < n ; ++i){
now.push_back(candidates[i]);
sum += candidates[i];
dfs(candidates,i); //下一次选数还可以继续从[i,n)选
sum -= candidates[i]; //恢复现场
now.pop_back();
}
}
};
5 字母大小写全排列

题目解析:给定一个由英文字母和数字字符组成的字符串,我们可以将英文字母进行大小写转换,要求我们返回所有转换之后可以得到的字符串。
本题也很简单,我们对于原字符串的每一个位置判断是否为字母,同时在决策树上分出两个分支来分别递归大写和小写就行了。
代码如下:
class Solution {
public:
string s;
vector<string> res;
int n;
vector<string> letterCasePermutation(string s1) {
s = s1;
n = s.size();
dfs(0); //转换[0,n)的子串
return res;
}
void dfs(int idx){
if(idx == n) return res.push_back(s);
dfs(idx+1); //不管是不是字母,原始的数字/大写/小写 本身就是一种情况
if(isupper(s[idx])) {
s[idx] = tolower(s[idx]);
dfs(idx+1);
}
else if(islower(s[idx])){ //注意这里要用else if ,如果用if,在s[idx]为大写时会重复计算
s[idx] = toupper(s[idx]);
dfs(idx+1);
}
}
};
11 优美的排列

题目解析:给定n个数1~n,要求我们将这n个数放进大小为n的数组中,如果满足perm[i]%i==0 || i%perm[i] == 0 ,对于所有的i (perm下标从1开始)都满足,那么这就是一个优美序列,要求我们返回优美序列的个数。
那么本题本质上还是一个在空位上选数填入的思路,只不过选数的时候多了一些条件,也就是需要能够被整除。
本题的剪枝策略其实就是优美序列的规则。
代码如下:
class Solution {
public:
bool use[16] = {false};
int n;
int res = 0;
int countArrangement(int n1) {
n = n1;
dfs(1);
return res;
}
void dfs(int idx){ //填idx位置
if(idx == n + 1) {
res++;
return;
}
for(int i = 1; i <= n ; ++i){
if(!use[i] && (idx % i == 0 || i % idx == 0)) {
use[i] = true;
dfs(idx+1);
use[i] = false;
}
}
}
};12 N 皇后
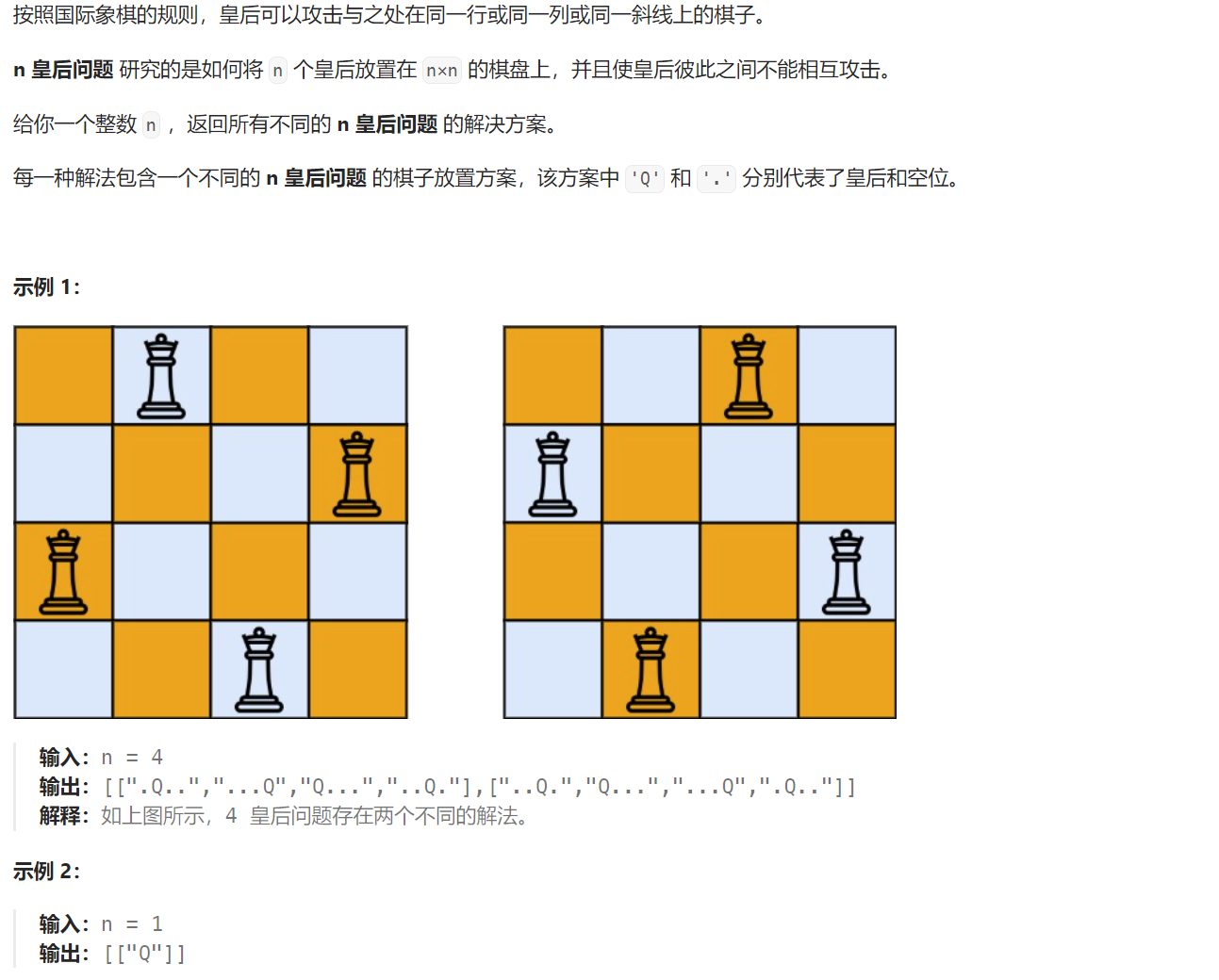
题目解析:本题是回溯的经典例题N皇后,给定n个皇后和一个n*n的棋盘,我们需要在棋盘中放置这n个皇后,同时需要使得这n个皇后不会相互攻击,那么在什么情况下会相互攻击呢?同一行或者同一列或者同一斜线的皇后会相互攻击。 我们需要返回所有的使得n个皇后不会相互攻击的防治方案。
初看本题可能会觉得不相互攻击的条件有些复杂,既要确保同一行没有皇后,同一列没有皇后,还需要确保同一斜线没有皇后,斜线既包括写了为1的斜线,也包括斜率为-1的斜线,这四个条件判断起来十分复杂。
其实我们可以先简化掉一个条件,由于同一行的皇后不能相互攻击,那么意味着每一行都必须有且只有一个皇后,那么我们可以按照行来进行划分,每一行都分配一个皇后,那么我们在dfs的时候就只需要考虑剩余三个条件了。
而对于列来说,我们用一个 bool col[n] 的数组就能够标记该列是否已经放置皇后了。
但是如何处理斜线呢? 我们初中数学学习过一个概念叫做截距,既有相对于x轴的截距,也有相对于y轴的截距,而一条斜线的x轴的截距和y轴的截距式固定的,那么两个点,如果过该点斜率为-1的斜线 x轴截距相等,那么这两个点就在同一斜线,同理如果两个点,过这两个点斜率为1的斜线的x轴的截距相同,那么这两个点在同一斜线。
对于每一个皇后,我们都可以标记其斜率为1和-1的斜线于x轴的截距,后续如果出现截距相同的位置,说明位于同一斜线,会发生冲突。
假设我们的皇后位于 (x,y),那么他的斜率1和-1的斜线对于x轴的截距是多少呢? x-y 和 x+y
而x-y的取值范围都是 [-n,n] ,x+y的取值范围为 [0,2n],我们可以使用一个 bool x1[2n] 和 bool x2[2n] 来标记截距,标记 x-y+n 和 x+y 。
本题中我们不断进行标记以及判断是否相互攻击本质就是一种剪枝,基于N皇后规则的剪枝。
代码如下:
class Solution {
public:
bool col[9] = {false};
bool x1[19] = {false}; //斜率为1的截距
bool x2[19] = {false}; //斜率为-1的截距
int n;
vector<vector<string>> res;
vector<string> now;
vector<vector<string>> solveNQueens(int n1) {
n = n1;
now.resize(n,string(n,'.'));
dfs(0); //从第0行开始填
return res;
}
void dfs(int x){
if(x == n) return res.push_back(now);
for(int y = 0 ; y < n ; ++y){ //判断当前row行的第j列能否填
if(!col[y] && !x1[x - y + n] && !x2[x + y]){ //满足三者
now[x][y] = 'Q';
col[y] = x1[x - y + n] = x2[x + y] = true;
dfs(x+1);
col[y] = x1[x - y + n] = x2[x + y] = false; //恢复现场
now[x][y] = '.';
}
}
}
};
13 有效的数独



题目解析:本题给定一个9*9的数独,要求我们判断数独是否有效,数独有效的条件:每一行不能出现重复数字,每一列不能出现重复数字,从上到下从左往右划分出的 3*3 的小九宫格不能有重复数字。
本题其实很简单,使用标记数组就行了,使用 row[9][10] 标记每个数字是否在每一行出现过,使用col[9][10] 标记每个数字是否在每一列出现过,使用 grid[3][3][10] 标记每一个数字是否在小九宫格内出现过。
本题使用循环就可以解决了,讲解本题主要是为了下一个题做铺垫。
代码如下:
class Solution {
public:
bool row[9][10] = {false};
bool col[9][10] = {false};
bool grid[3][3][10] = {false};
bool isValidSudoku(vector<vector<char>>& board) {
for(int i = 0 ; i < 9 ; ++i){
for(int j = 0 ; j < 9 ; ++j){
if(board[i][j] == '.') continue;
int n = board[i][j] - '0';
if(row[i][n] || col[j][n] || grid[i/3][j/3][n]) return false;
row[i][n] = col[j][n] = grid[i/3][j/3][n] = true;
}
}
return true;
}
};
14 解数独



题目解析:本题给定一个数独,要求我们将空白位置填值,解数独。
那么我们在对空白位置填值的时候,就需要遵循数独的规则,行,列和小九宫格不能出现重复数字,如何快速判断某个数字是否满足条件呢?可以用到我们上一题使用的三个标记数组。
同时,我们的dfs可以设置一个返回值,如果某一次递归到叶子节点,说明数独已经解出来了,此时直接返回true,而前面的函数栈帧在接收到true之后也可以直接返回,因为我们已经求出数独的解了。
代码如下:
class Solution {
public:
vector<pair<int,int>> tofill; //待填位置
int n;
bool row[9][10] = {false};
bool col[9][10] = {false};
bool grid[3][3][10] = {false};
void solveSudoku(vector<vector<char>>& board) {
for(int i = 0 ; i < board.size(); ++i)
for(int j = 0 ; j < board[0].size(); ++j)
if(board[i][j] == '.') tofill.emplace_back(i,j);
else{
int n = board[i][j] - '0';
row[i][n] = col[j][n] = grid[i/3][j/3][n] = true; //标记原有数据
}
n = tofill.size();
dfs(board,0); //从第0个空位开始填
// return res;
}
bool dfs(vector<vector<char>>& board , int index){
if(index == n) return true; //填完
auto [x,y] = tofill[index];
for(int i = 1 ; i <= 9 ; ++i){
if(!row[x][i] && !col[y][i] && !grid[x/3][y/3][i]){
//可以填i
board[x][y] = '0' + i;
row[x][i] = col[y][i] = grid[x/3][y/3][i] = true;
if(dfs(board,index+1)) return true;
row[x][i] = col[y][i] = grid[x/3][y/3][i] = false; //恢复现场
// board[x][y] = '.';
}
}
//说明index-1枚举的数字不能够解出来数独,需要在上一层或者前面的位置继续修改,也就是回溯
return false;
}
};
15 单词搜索

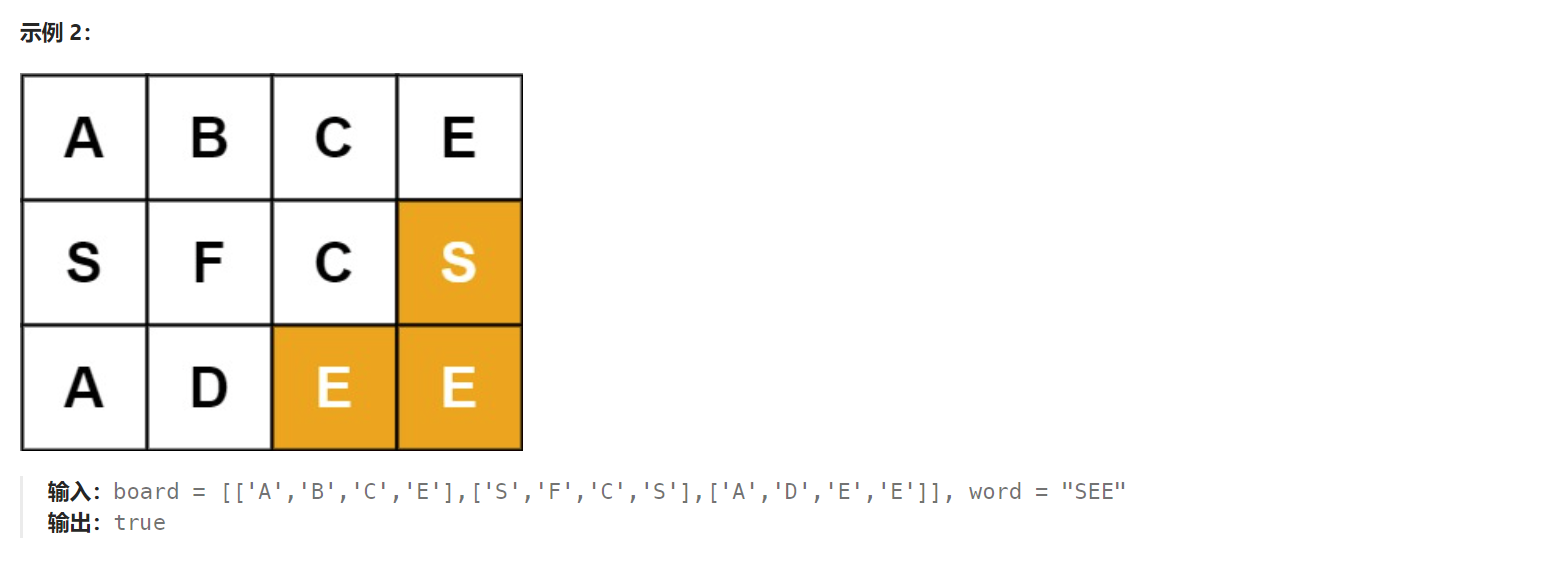

题目解析:给定一个待寻找的单词和一个存储字母的二维数组,我们需要判断在二维数组中能否找到一条路径,使得路径上的字母组合成的单词式待查找的单词。
本题可以使用bfs也可以使用dfs,但是dfs的回溯更简单,我们只需要找到第一个字母的位置,然后以该位置进行dfs就行了,同时为了防止走回头路,我们还需要一个vis数组来进行标记。
代码如下:
class Solution {
public:
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
bool vis[6][6] = {false};
string s; //存储当前路径的单词
int len;
int m , n;
bool exist(vector<vector<char>>& board, string word) {
len = word.size();
s.resize(len);
m = board.size() , n = board[0].size();
for(int i = 0 ; i < m ; ++i){
for(int j = 0 ; j < n ; ++j){
if(board[i][j] == word[0] && dfs(board , word ,i,j,1)) return true;
}
}
return false;
}
bool dfs(vector<vector<char>>& board , string& word , int x, int y , int index){ //标识从(x,y)附近去找word[index]
if(index == len) return true; //(x,y)是word的最后一个字母,说明前面已经找完了
vis[x][y] = true; //标记已使用
for(int i = 0 ; i < 4 ; ++i){
int row = x + dx[i] , col = y + dy[i];
if(row >= 0 && row < m && col >= 0 && col < n && !vis[row][col] && board[row][col] == word[index]){
if(dfs(board,word,row,col,index+1)) return true;
}
}
vis[x][y] = false; //恢复现场
return false;
}
};
16 黄金矿工
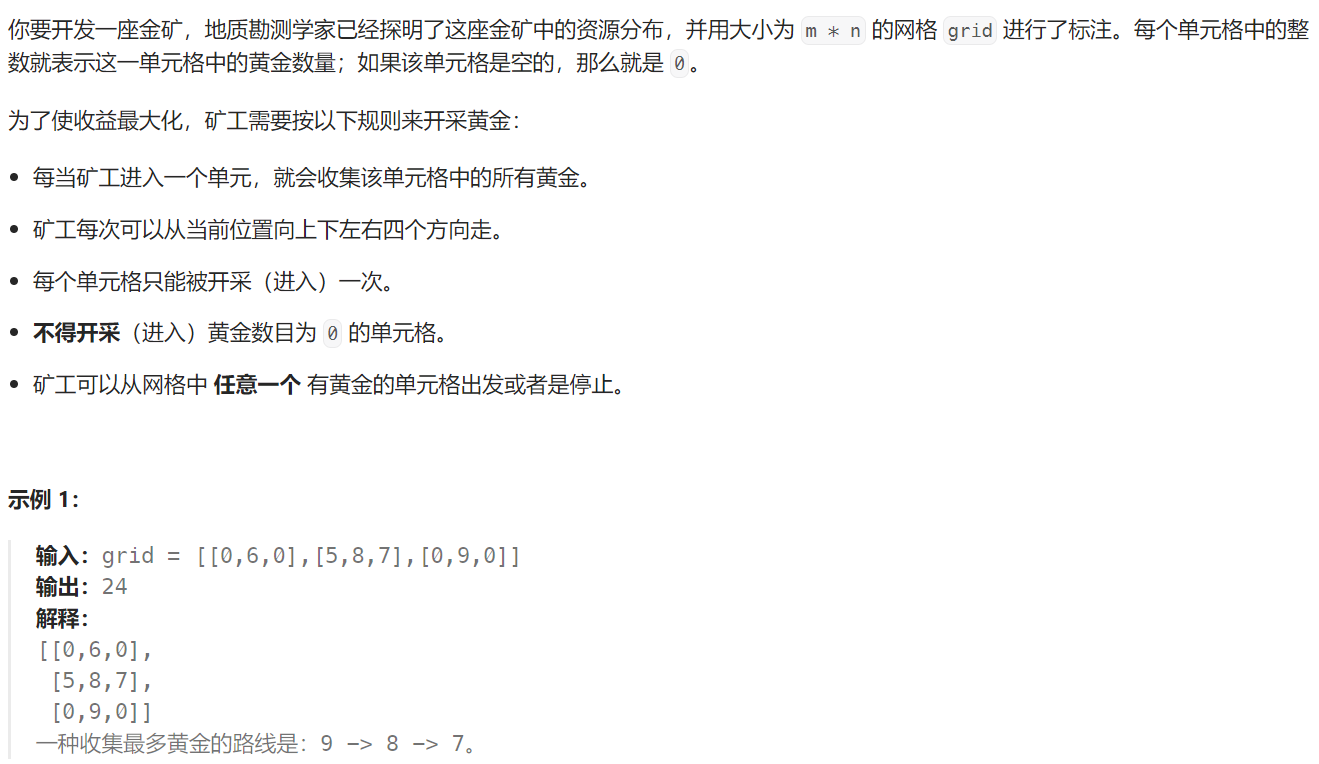

题目解析:给定一个二维数组表示每个位置的黄金数量,矿工在开采时,从一个有黄金的起点出发,可以向上下左右四个方向移动,但是移动的前提必须是该位置必须有黄金(如果被开采过了则相当于没有黄金),直到走到某一个位置之后无法再移动,整条路径的黄金总数就是开采的黄金,返回矿工一次开采能拿到的最大的黄金数量。
那么本题其实要我们求一个最长路径,其实我们直接以每一个有黄金的位置为起点做一次bfs就行了。假设当前我们位于 (x,y) ,我们下一步可以走向 (x1,y1) 或者 (x2,y2) ,我们走(x1,y1)这条路径有一个可以开采的最大黄金数量w1,走(x2,y2)这条路径也有一个可以开采到的最大黄金数量w2,那么我们可以认为从(x,y)出发(当然x,y 可能是一条路径的中间节点而不是最起始)的能开采到的最大黄金数量就是 grid[x][y] + max(w1,w2),我们会接着返回给上一层dfs。
代码如下:
class Solution {
public:
bool vis[15][15] = {false};
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int m;
int n;
int res = 0;
int getMaximumGold(vector<vector<int>>& grid) {
m = grid.size() , n = grid[0].size();
for(int i = 0 ; i < m ; ++i)
for(int j = 0 ; j < n ; ++j)
if(grid[i][j] != 0) res = max(res , dfs(grid,i,j));
return res;
}
int dfs(vector<vector<int>>& grid,int row , int col){
int res = grid[row][col];
vis[row][col] = true; //标记访问,放置回头路
//探测周围点
for(int i = 0 ; i < 4 ; ++i){
int x = row + dx[i] , y = col + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != 0 && !vis[x][y]){
res = max(res , grid[row][col] + dfs(grid,x,y));
}
}
//恢复现场
vis[row][col] = false;
return res;
}
};
17 不同路径 III


题目解析:本题给定一个二维网格图,给定一个起点和终点,同时网格图中还有一些空位和障碍,空位是我们能够走的位置,障碍不能走。我们需要从起点走到终点,同时这条路径中需要包含所有的空位,以及不能重复走某些空位,要求我们返回有多少条这样的路径。
那么我们还是可以直接以起点进行dfs,除了需要标识每一个位置是否走过来避免回头路死递归之外,我们还需要记录一下走到当前位置一共走过了多少个空位置。当我们走到终点的时候,如果走过的空位数和总的空位数相等,那么这是一条我们需要的路径,如果不相等,这条路径不是我们所需要的,不需要增加结果的计数,但是也需要直接返回。
代码如下:
class Solution {
public:
int total = 0; //总的空位数
int m ;
int n ;
bool vis[20][20] = {false};
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int endi,endj;
int res;
int uniquePathsIII(vector<vector<int>>& grid) {
int r ,c;
m = grid.size() , n = grid[0].size();
for(int i = 0 ; i < m; ++i)
for(int j = 0 ; j < n ; ++j)
if(grid[i][j] == 0) ++total;
else if(grid[i][j] == 1) r = i , c = j;
else if(grid[i][j] == 2) endi = i , endj = j;
vis[r][c] = true;
dfs(grid,r,c); //从起点开始做一次dfs
return res;
}
void dfs(vector<vector<int>>& grid , int row , int col){
if(row == endi && col == endj){ //走到终点
if(total == 0) res++;
return;
}
//直接枚举周围四个位置能不能走
for(int i = 0 ; i < 4 ; ++i){
int x = row + dx[i] , y = col+ dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != -1 && !vis[x][y]){
if(grid[x][y] == 0)--total; //走到下一个空位,计数减减
vis[x][y] = true;//标记
dfs(grid,x,y);
if(grid[x][y] == 0)++total; //恢复现场
vis[x][y] = false;
}
}
}
};
五 FloodFill
FloodFill类型的题目我们再BFS专题中已经使用BFS解决过了,因为FloodFill也可以使用DFS来解决,所以在本章节中也会包含使用DFS解决的FloodFill题目,不过可能会与BFS专题中的FloodFill的例题重叠。
1 图像渲染

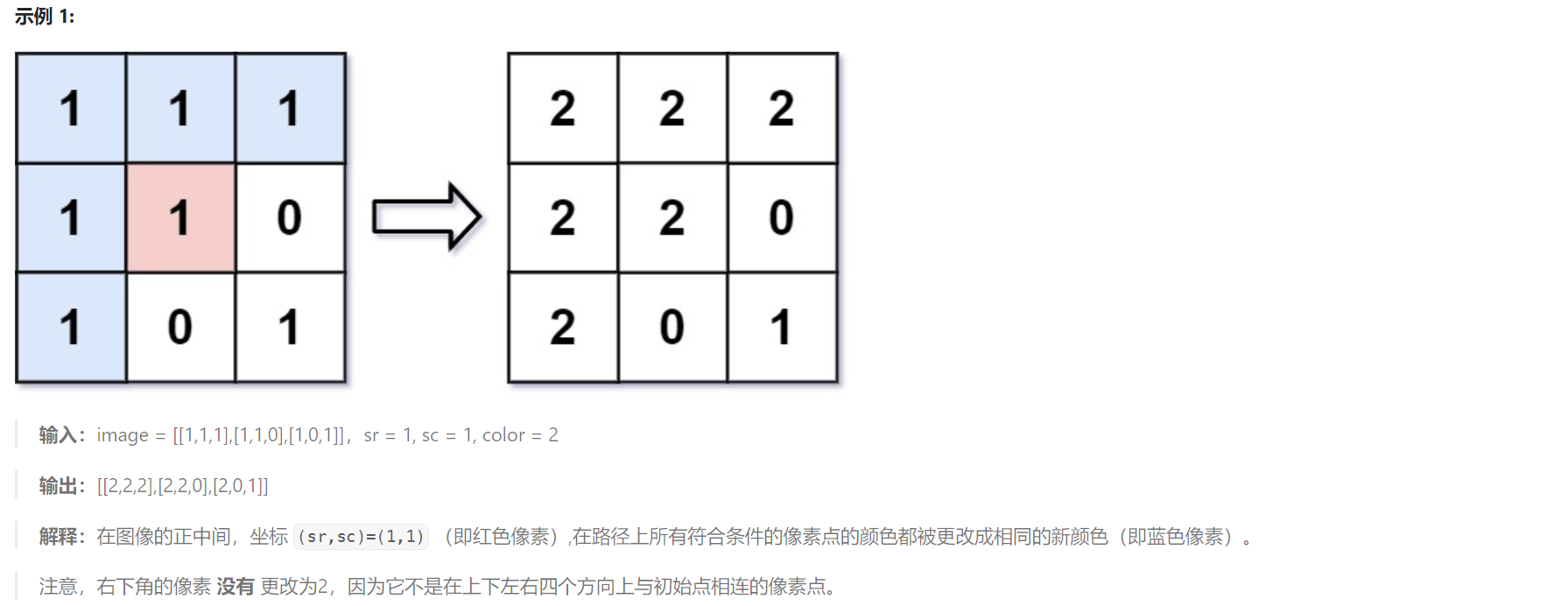

题目解析:本题给定一个二维像素数组,给定一个渲染的起始位置,要求我们从起始位置开始,将与起始位置相邻且颜色相同的位置都染色成 color ,其余位置不动,返回修改之后的数组。
那么我们还是以起始位置为起点做一次dfs,如果相邻位置颜色与起始位置的原始颜色相同, 我们就将其颜色修改为color,同时以该位置为起点继续做一次dfs。
代码如下:
class Solution {
public:
int col,color;
int m,n;
int dx[4] = {1,-1,0,0};
int dy[4] = {0,0,1,-1};
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color1) {
m = image.size(),n = image[0].size(),col = image[sr][sc],color = color1;
if(col != color) dfs(image,sr,sc);
return image;
}
void dfs(vector<vector<int>>& image, int i , int j){
image[i][j] = color;
for(int k = 0 ; k < 4 ; ++k){
int x = i + dx[k] , y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == col)dfs(image,x,y);
}
}
};
2 岛屿数量

题目解析:给定一个二维数组,二维数组中的值为1表示当前位置为陆地,为0表示海洋,相连的陆地构成岛屿,要求我们求出岛屿的数量。
求岛屿的数量起始就是在求1的联通块的数量,我们还是以每一个未标记的1为起点做一次DFS,将与其直接和间接相连的位置标记,表示该陆地已经属于一个岛屿。 那么我们进行了多少次DFS就有多少个岛屿。
代码如下:
class Solution {
public:
int m , n ;
int res;
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int numIslands(vector<vector<char>>& grid) {
m = grid.size() , n = grid[0].size();
for(int i = 0 ; i < m ; ++i){
for(int j = 0 ; j < n ; ++j)
if(grid[i][j] == '1')dfs(grid,i,j),++res;
}
return res;
}
void dfs(vector<vector<char>>& grid , int row , int col){
grid[row][col] = '2';
for(int i = 0 ; i < 4 ; ++i){
int x = row + dx[i] , y = col + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == '1') dfs(grid,x,y);
}
}
};
3 岛屿的最大面积


题目解析:给定一个二维数组,1表示陆地,0表示海洋,相连的陆地构成岛屿,本题要求我们返回图中最大的岛屿的面积或者说陆地数。
那么本题就是求最大的1的连通块,我们可以使用全局变量进行记录和回溯。
代码如下:
class Solution {
public:
int s , res;
int m , n;
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int maxAreaOfIsland(vector<vector<int>>& grid) {
m = grid.size() , n = grid[0].size();
for(int i = 0 ; i < m ; ++i)
for(int j = 0 ; j < n ; ++j)
if(grid[i][j] == 1) s = 0 , dfs(grid,i,j);
return res;
}
void dfs(vector<vector<int>>& grid , int row , int col){
grid[row][col] = 2; //标记已经在其它岛屿计算过了,防止重复计算
++s;
for(int i = 0 ; i < 4 ; ++i){
int x = row + dx[i] , y = col + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1)dfs(grid,x,y);
}
res = max(s,res);
}
};
4 被围绕的区域
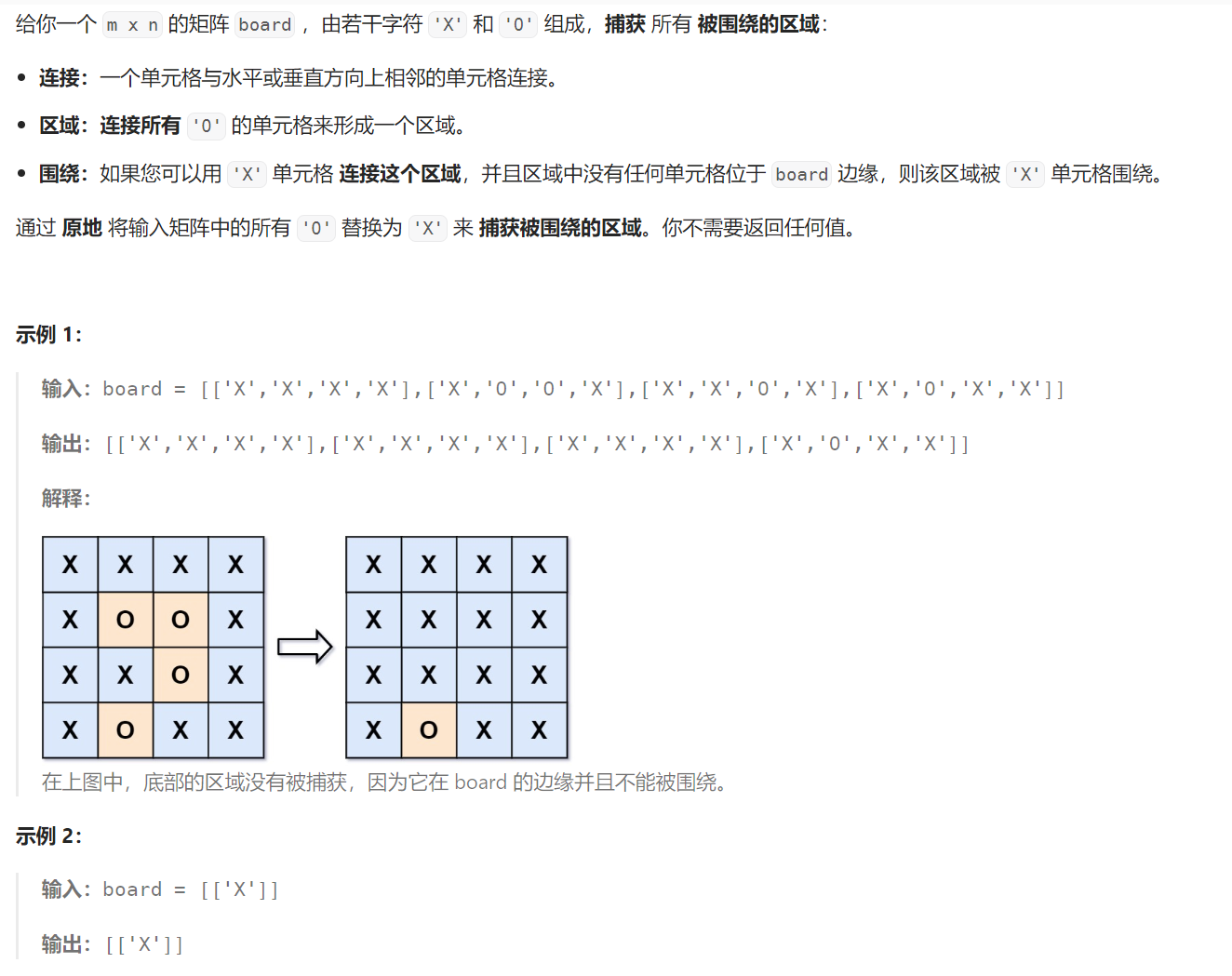
题目解析:给定一个二维数组,我们需要将所有被X完全围绕的O修改为X。
位于边界的O是不被X完全围绕的,所以我们可以以所有的边界的O为起点,dfs 来标记所有未被X完全包围的O,比如修改为'A',在标记完所有未被围绕的O之后,再遍历一遍board,遍历过程中所有的O都是被X完全围绕的了,修改为X,而A表示未被围绕的O,我们将其修改回O。
代码如下:
class Solution {
public:
int m ,n;
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
void solve(vector<vector<char>>& board) {
m = board.size() , n = board[0].size();
//找边界的O为起点进行DFS,标记未被围绕的O
for(int i = 0 ; i < m ; ++i){
if(board[i][0] == 'O') dfs(board,i,0);
if(board[i][n-1] == 'O') dfs(board,i,n-1);
}
for(int j = 0 ; j < n ; ++j){
if(board[0][j] == 'O') dfs(board,0,j);
if(board[m-1][j] == 'O') dfs(board,m-1,j);
}
for(int i = 0 ; i < m ; ++i){
for(int j = 0 ; j < n ; ++j){
if(board[i][j] == 'O') board[i][j] = 'X';
if(board[i][j] == 'A') board[i][j] = 'O';
}
}
}
void dfs(vector<vector<char>>& board , int row , int col){
board[row][col] = 'A';
for(int i = 0 ; i < 4 ; ++i){
int x = row + dx[i] , y = col + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O')dfs(board,x,y);
}
}
};
5 太平洋大西洋水流问题

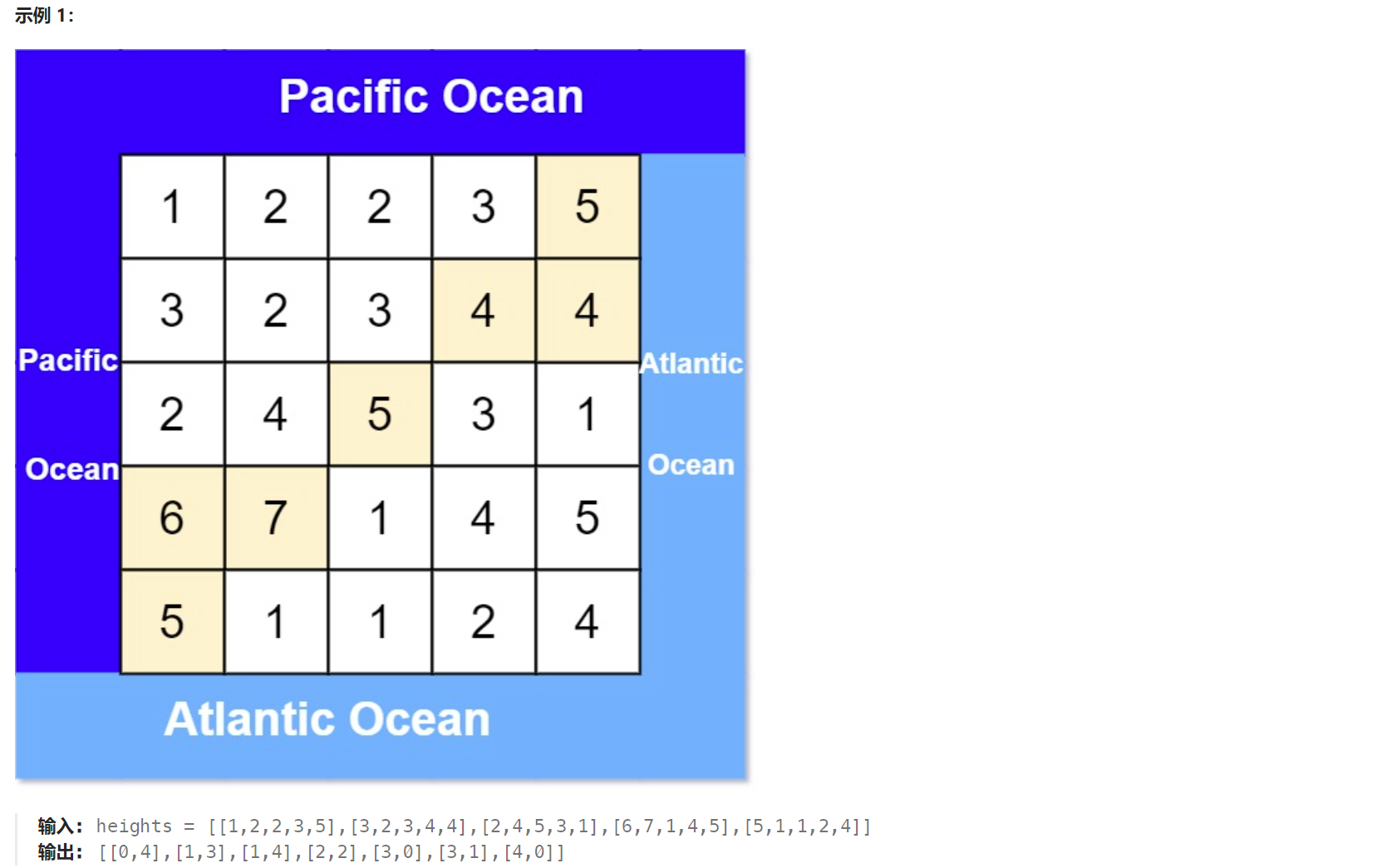

题目解析:给定一个二维数组,每一个元素表示该位置的高度,我们可以认为每一个位置都在下雨,对于一个位置,他的雨水能够流向与他相邻的同时高度和他相等或者比他低的位置。二维数组的左外边界和上外边界是太平洋,右外边界和下外边界是大西洋,我们需要求出哪一些位置的雨水既可以流向大西洋也可以流向太平洋,返回这些位置的下标。
比如例一中的(0,4),他直接就与太平洋和大西洋相连,所以满足条件。又比如 (1,4),它可以直接流向大西洋,也可以通过 (1,4)->(1->3)->(0->3)->太平洋 从而流向太平洋,所以也满足条件。
那么我们如何去求呢?还是逆向思维,能够流向太平洋的位置一定都必须经过左边界或者上边界的点,那么我们以所有左边界和上边界的点为起点做dfs,就能求出所有的能够流向太平洋的位置。
同时所有能够流向大西洋的位置一定需要经过有边界或者下边界,那么我们以有边界和下边界的点为起点做dfs,就能求出所有的能够流向大西洋的位置。
当某个位置既能够流向太平洋又能够流向大西洋,那么这就是我们所需要的位置。
代码如下:
class Solution {
public:
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
bool vis[200][200] = {false};
int cnt[200][200] = {0}; //记录每一个位置是否能够流向太平洋或者大西洋
int m , n;
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
m = heights.size() , n = heights[0].size();
//计算能流向太平洋的位置
for(int i = 0 ; i < m ; ++i){
if(!vis[i][0])dfs(heights,i,0);
}
for(int j = 0 ; j < n ;++j){
if(!vis[0][j])dfs(heights,0,j);
}
//此时所有能够流向太平洋的位置的计数都+1了
memset(vis,false,sizeof vis);
//计算能够流向大西洋的位置
for(int i = 0 ; i < m ; ++i){
if(!vis[i][n-1])dfs(heights,i,n-1);
}
for(int j = 0 ; j < n ; ++j){
if(!vis[m-1][j])dfs(heights,m-1,j);
}
//此时所有能够流向大西洋的位置计数器+1
//那么既能够流向太平洋又能够流向大西洋的位置的计数就是2
vector<vector<int>> res;
for(int i = 0 ; i < m ; ++i)
for(int j = 0 ; j < n ; ++j)
if(cnt[i][j] == 2) res.push_back({i,j});
return res;
}
void dfs(vector<vector<int>>& heights , int row , int col){
vis[row][col] = true;
cnt[row][col]++;
for(int i = 0 ; i < 4 ; ++i){
int x = row + dx[i] , y = col + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && heights[row][col] <= heights[x][y])dfs(heights,x,y);
}
}
};
6 扫雷游戏



题目解析:给定两个二维网格,代表着一次扫雷游戏的盘面,board是每个位置是否为雷,M表示未挖出的地雷,E表示未挖出的空方块, B表示已挖出的周围没有地雷的方块,数字字符表示已挖出的方块周围的地雷的数量(八联通),X表示已挖出的地雷。而click则是我们点击的位置。
点击一个位置之后展开规则如下:
1、如果点击位置是雷,那么board的该位置修改为X,此时游戏结束,直接返回。
2、如果点击位置的周围八个位置中有至少一个地雷,那么不再展开,而是修改为数字字符后返回。
3、如果点击位置的周围八个位置都没有地雷,那么修改为B,并展开到周围的未挖开的位置去。
本题其实题目理解起来有点复杂,但是我们读一遍题目之后还是很简单的,只需要从点击位置做一次dfs就行了,根据展开规则来判断是否需要返回或者继续展开。
代码如下:
class Solution {
public:
int dx[8] = {0,0,1,-1,1,-1,1,-1};
int dy[8] = {1,-1,0,0,1,-1,-1,1};
int m,n;
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {
m = board.size(),n = board[0].size();
dfs(board,click[0],click[1]);
return board;
}
bool dfs(vector<vector<char>>& board,int row , int col){ //返回值无意义,只是因为在前两种情况返回的时候不想写成两条语句
//展开(row,col)
//1、如果是雷直接修改返回
if(board[row][col] == 'M') return board[row][col] = 'X';
//2、看周围八个位置是否有雷以及雷的数量
int cnt = 0;
for(int i = 0; i < 8 ; ++i){
int x = row + dx[i] , y = col + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'M') ++cnt;
}
//有雷的话不展开了,修改返回
if(cnt > 0) return board[row][col] = cnt+'0';
//没有雷则继续展开
board[row][col] = 'B';
for(int i = 0; i < 8 ; ++i){
int x = row + dx[i] , y = col + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'E') dfs(board,x,y);
}
return true;
}
};
7 衣橱整理

题目解析:给定一个二维数组,每一个位置都是待整理的格子,整理师从(0,0)开始整理,每一次可以向右也可以向下走一步,但不能走到数组外面,对于 grid[x][y] ,如果 digit(x) + digit(y)> cnt,那么(x,y)这个各自不需要整理,也就是不能走到这个位置。 digit(num)表示num的每一位数字之和。我们需要返回整理师一共需要整理多少个格子。
由于需要返回的是总共需要整理的格子数量,也就是说整理师可能不止从(0,0)开始走一次,而可能需要走多次才能把所有可整理的格子整理完。
那么我们就可以将题目转换一下,既然需要走多次,那么题目的限制:只能向下和向右走其实可以忽略,我们认为可以往回走,这样一来就可以转换为dfs的思路。当然其实实际上dfs的每一条到叶子节点的路径都是整理师完整走一遍的。
代码如下:
class Solution {
public:
int m , n , cnt;
int dx[4] = {0,1};
int dy[4] = {1,0};
bool vis[100][100] = {false};
int res = 0;
int wardrobeFinishing(int m1, int n1, int cnt1) {
m = m1 , n = n1 , cnt = cnt1;
dfs(0,0);
return res;
}
void dfs(int row , int col){
//dfs往下走的时候还是只能向右或者向下
//由于 先向右再向下 和 先向下再向右可能走到同一个位置,那么我们需要一个标记数组来确保每一个位置只整理一次
//判断本位置能否走到
int sum = 0 , num = row;
while(num) {
sum += num % 10;
num /= 10;
}
num = col;
while(num){
sum += num%10;
num /= 10;
}
if(sum > cnt) return;
++res; //走到这里说明(row,col)需要整理
vis[row][col] = true;
//然后扩展周围两个位置
for(int i = 0 ; i < 2 ; ++i){
int x = row+ dx[i] , y = col + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) dfs(x,y);
}
}
};
六 记忆化搜索
记忆化搜索是基于递归的,在递归的过程中,将某些参数的递归函数的执行结果存储起来,后续再调用相同的函数和参数的时候,直接从保存的结果中取出来,而不去重复递归。在逻辑上,记忆化搜索有点类似于我们之前学习的动态规划,记忆化搜索需要一个memo数组来存储某些参数的递归函数的结果,而对应动态规划而言就是我们的dp数组。 当然这两个本质还是有所区别,有些场景这两种方法都适用,而有些方法则使用其中一种更方便,能大幅减轻代码的复杂度,逻辑更加简单。
1 斐波那契数

题目解析:本题需要我们求第n个斐波那契数。
如果我们简单使用递归的话,那么就是dfs(n) = dfs(n-1) + dfs(n-2)。此时我们将递归展开,比如dfs(5) = dfs(4) + dfs(3) = dfs(3) + dfs(2) + dfs(2) + dfs(1) = dfs(2) + dfs(1) + dfs(1) + dfs(0) + dfs(1) + dfs(0) + dfs(1) = dfs(1) + dfs(0) + dfs(1) + dfs(1) + dfs(0) + dfs(1) + dfs(0) + dfs(1)。
一个简单的dfs(5)就需要展开8条递归路径,如果n更大,那么函数栈帧展开更多。但是我们注意到,比如 dfs(5) = dfs(4) + dfs(3) ,此时我们会先去算 dfs(4) = dfs(3) + dfs(2) ,那么在dfs(4)返回之后,其实我们已经算过dfs(3)了,后续 + dfs(3)的时候其实并没有必要再去递归一遍,如果我们在第一次计算dfs(3)返回之前将结果保存到一个全局的 memo 数组,那么后续算完dfs(4)之后要求dfs(3)的值我们就只需要在memo数组拿出来就行了,省去了一次dfs(3)的递归调用。这还仅仅是n==5的时候,如果n更大,我们节省的调用更多,同时,这样一来我们其实能够确保每一个dfs(i)都只求一遍,类似于动态规划。
使用记忆化搜索的时候一般需要以下步骤:
1、维护好一个memo数组。
2、编写好基础的递归函数
3、在递归函数开始的时候看一下memo数组中是否已经有本次调用的结果,如果有直接返回。
4、递归函数返回之前,将结果保存到memo数组中。
代码如下:
class Solution {
public:
int memo[31];//memo[i] == 0表示未计算过,
int fib(int n) {
for(auto x : memo) cout<<x<<endl;
return dfs(n);
}
int dfs(int x){
if(memo[x]) return memo[x];
//走到这里说明没有计算过dfs(x)
if(x <= 1) memo[x] = x;
else memo[x] = dfs(x-1) + dfs(x-2); //记录结果
return memo[x];
}
};
2 不同路径


题目解析:给定一个m*n的网格图,机器人从左上角出发,每一次向右或者向下走,问走到右下角有多少种方式。
如果使用暴搜的情况下,我们dfs(x,y)需要返回 dfs(x-1,y)+dfs(x,y-1),也就是上一步总共有多少种方式,那么我们基于暴搜进行优化,可以是用一个二维的memo数组来存储dfs(x,y)的返回值。
而我们递归的返回条件就是 x==0 && y==0也就是起点,其实我们可以在递归之前初始化一下memo[0[0],这样一来我们就不需要考虑起点了,而是将起点也当成一个普通的点来看。
代码如下:
class Solution {
public:
int memo[100][100]; //memo[x][y] == 0 表示未计算过
int uniquePaths(int m, int n) {
memo[0][0] = 1;
return dfs(m-1,n-1);
}
int dfs(int x , int y){
if(memo[x][y] != 0) return memo[x][y];
if(x > 0) memo[x][y] += dfs(x-1,y);
if(y > 0) memo[x][y] += dfs(x,y-1);
return memo[x][y];
}
};
3 最长递增子序列

题目解析:题目给定一个整数数组,要求我们求出最长的严格递增子序列的长度。
如果使用暴搜的思路,那么我们首先需要枚举出所有的递增子序列,然后记录最长的递增子序列的长度就行了。
那么我们可以枚举递增子序列的起点,比如dfs(x)中会枚举出以nums[x]为起点的所有递增子序列,同时返回最长的递增子序列的长度。我们会遍历 0~n 都求一遍 dfs(x),然后记录最大的返回值就行了。
而在枚举以x为起点的递增子序列的时候,我们可以看成在[x+1,n-1]范围内的一个递增子序列的前面接上一个nums[x] ,那么要使得这个递增子序列前面能接上nums[x],必须要满足该递增子序列的第一个元素nums[y]大于nums[x],所以我们只需要枚举出所有的nums[y]就行了,而以nums[x]为起点的递增子序列的最大长度就是所有的nums[y]为起点的递增子序列的最大长度+1。
而记忆化我们可以记录以 x 为起点的最长递增子序列的长度为memo[x]。
代码如下:
class Solution {
public:
int n;
int memo[2500]; //为0表示未记录过
int lengthOfLIS(vector<int>& nums) {
n = nums.size();
int res = 0;
for(int i = 0 ; i < n ; ++i) res = max(res , dfs(nums,i));
return res;
}
int dfs(vector<int>& nums , int x){
if(memo[x] != 0) return memo[x]; //说明已经计算过
int len = 1;
for(int j = x + 1 ; j < n ; ++j){
if(nums[j] > nums[x]) len = max(len,1 + dfs(nums,j));
}
memo[x] = len;
return len;
}
};
4 猜数字大小 II

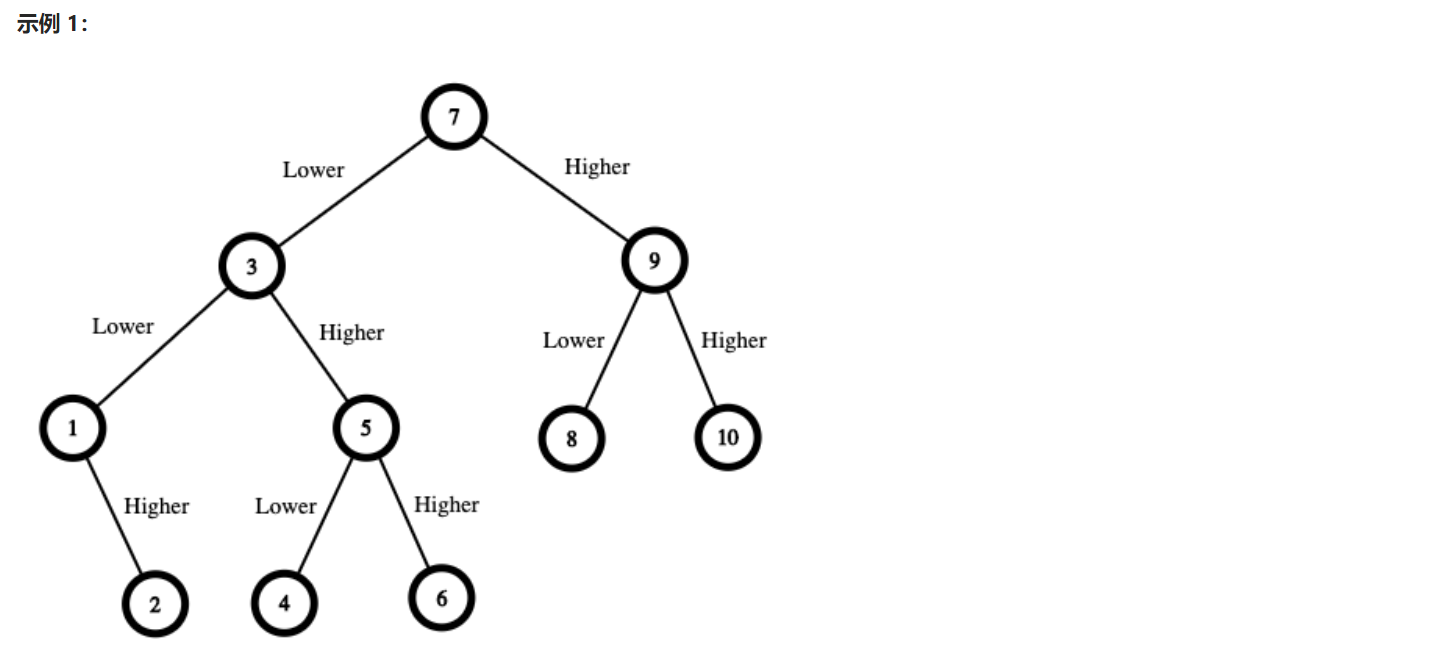


题目解析:给定一个数字n来进行数字游戏,在1~n之间选中一个数target作为结果,我们需要进行猜数,当我们猜 x 而x不是target时,此时我们需要支付x的惩罚费用,当我们猜中x==target时,不需要支付费用,游戏结束。
而target可能是1~n的任意一个数,那么就要求不管我们要猜的数是多大,他的最大代价要最小,也就是我们设计猜数策略的时候,不是要求某一个数的代价最小,而是要求在整个猜数过程中,某一个数的花费是最大的,而我们要求这个最大代价最小。
在设计dfs的时候,我们需要传进传入猜数的范围[begin,end],那么本轮我们可以猜[begin,end]的任意数,比如我们猜 x ,如果x==target ,那么此时不需要支付,游戏结束,如果target < x,那么我们本轮花费了x,同时下一轮还需要继续猜,同理target>x的时候也需要支付x。那么不管target是在[begin,x-1]还是在[x+1,end],通过dfs(begin,x-1)能够求出在[begin,x-1]猜数所需的最小代价c1,通过dfs(x+1,end)能够求出在[x+1,end]猜数所需的最小代价c2,那么在本轮选x的情况下,确保我们的钱足够在[begin,end]范围内猜中任意数,那么至少需要s = x + max(c1,c2)。
而我们通过在[begin,end]枚举本轮猜的数x,能够得出所有的s,我们需要的是最优的方案也就是最大代价较小,那么需要返回的就是 min(s)。
那么我们的暴搜的思路写成代码如下:
class Solution {
public:
int getMoneyAmount(int n) {
return dfs(1,n);
}
int dfs(int begin, int end){
//枚举猜的数x
if(begin >= end) return 0;//只有一个数或者范围无效时,不需要花费
int res = INT_MAX;
for(int x = begin; x <= end; ++x){
int cost = 0; //猜中的话就是0
//如果没猜中,那么结果如果在[begin,x-1]
cost = x + dfs(begin,x-1);//返回在[begin,x-1]在最优情况下,需要花费的最大价值(在最优情况下有一个数所需要的花费最大)
//也可能在[x+1,end]
cost = max(cost,x + dfs(x+1,end)); //两种情况都需要能够才出来,那么需要这两种情况的最小花费的较大值
res = min(res,cost);
}
return res;
}
};
在这种情况下,由于在暴搜的过程中有很多的重复调用,时间复杂度很低,在第9个测试用例就超时了,为了防止过多的重复调用,我么可以使用记忆化,将求出的结果记录在数组中。
我们使用memo[x][y] 来保存在[x,y]范围内猜数所需的最小代价,那么后续再次调用dfs(x,y)的时候,如果memo[x][y] 填过了,就可以直接返回memo[x][y]。
代码如下:
class Solution {
public:
vector<vector<int>> memo;
int getMoneyAmount(int n) {
memo.resize(n+1,vector<int>(n+1,-1)); //-1表示没填过
//memo[x][y]记录在[x,y]猜数的最小代价
return dfs(1,n);
}
int dfs(int begin, int end){
//由于枚举的时候可能会枚举x到n,那么此时begin 可能为n+1,会越界,所以边界情况我们可以提前返回,不做记录
if(begin >= end) {
return 0;//只有一个数或者范围无效时,不需要花费
}
if(memo[begin][end] != -1) return memo[begin][end];
int res = INT_MAX;
//枚举猜的数x
for(int x = begin; x <= end; ++x){
int cost = 0; //猜中的话就是0
//如果没猜中,那么结果如果在[begin,x-1]
cost = x + dfs(begin,x-1);//返回在[begin,x-1]在最优情况下,需要花费的最大价值(在最优情况下有一个数所需要的花费最大)
//也可能在[x+1,end]
cost = max(cost,x + dfs(x+1,end)); //两种情况都需要能够才出来,那么需要这两种情况的最小花费的较大值
res = min(res,cost);
}
memo[begin][end] = res; //进行记忆化
return res;
}
};
以上的4个题其实改成动态规划都不难,这些题就是典型的既可以是用动态规划也可以使用记忆化搜索,两种做法都不难想的题目,但是有些题目更适合使用记忆化搜索或者动态规划来做。比如在求路径的时候为了防止走回头路或者重复走某一个位置,我们就需要dfs的vis数组来进行记录和标识,以及回溯等操作,这样的话使用记忆化搜索会更简单。
5 矩阵中的最长递增路径


题目解析:给定一个二维矩阵,我们需要在矩阵中找出最长递增路径的长度。
使用暴搜的话,我们会枚举所有位置为递增路径的长度,记录最长的递增路径的长度。
暴搜代码如下:
class Solution {
public:
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int m , n , res;
int longestIncreasingPath(vector<vector<int>>& matrix) {
m = matrix.size(), n = matrix[0].size();
//枚举所有位置为起点
for(int i = 0 ; i < m ; ++i){
for(int j = 0 ; j < n ; ++j) dfs(matrix,i,j,0);
}
return res;
}
void dfs(vector<vector<int>>& matrix , int sr , int sc , int len){
++len; //表示从起点到当前位置长度已经是len了
for(int i = 0 ; i < 4 ; ++i){
int x = sr + dx[i] , y = sc + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[sr][sc]) dfs(matrix,x,y,len);
}
res = max(res,len);
}
};
而本题使用暴搜是会超时的,为什么呢? 首先我们思考一个问题,就是为什么我们本题的暴搜不需要使用vis数组来记录每个位置是否被访问过?很简单,因为我们的访问路径是严格递增的,我们在(sr,sc)进行寻找下一步的时候,假设(sr,sc)的上一步是(x,y),那么一定有matrix[x][y] < matrix[sr][sc],而我们在寻找(sr,sc)的下一步的时候,要找的是大于matrix[sr][sc]的位置,一定不会走回头路。所以也就不需要vis数组来标记是否访问过。
那么本题我们可以使用记忆化来优化时间复杂度,使用memo[x][y]来记录以(x,y)为起点的最长递增路径的长度。那么后续我们调用dfs(x,y)的时候,就可以直接使用memo[x][y]的值来返回,避免重复调用。同时我们的dfs函数越需要修改,至少需要一个返回值。
代码如下:
class Solution {
public:
int memo[200][200]; //为0表示未填过,因为长度最少都是1
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int m , n , res;
int longestIncreasingPath(vector<vector<int>>& matrix) {
m = matrix.size(), n = matrix[0].size();
//枚举所有位置为起点
for(int i = 0 ; i < m ; ++i){
for(int j = 0 ; j < n ; ++j) dfs(matrix,i,j);
}
return res;
}
int dfs(vector<vector<int>>& matrix , int sr , int sc ){
if(memo[sr][sc] != 0) return memo[sr][sc];
int len = 1;
for(int i = 0 ; i < 4 ; ++i){
int x = sr + dx[i] , y = sc + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[sr][sc]){
len = max(len , 1 + dfs(matrix,x,y));
}
}
//返回之前记录一下memo同时更新一下res
res = max(len , res);
memo[sr][sc] = len;
return len;
}
};
总结
本文主要讲解dfs的几种应用场景,包括在数组,二叉树,图等结构上的暴搜,以及基于暴搜的回溯和剪枝的策略和做法,同时也使用记忆化搜索对暴搜进行优化,防止重复调用。