阿里云通义MoE全局均衡技术：突破专家负载失衡的革新之道-EW帮帮网

MoE模型的基本原理与核心价值

混合专家模型（Mixture of Experts，MoE）是当前AI大模型领域最重要的架构创新之一，其核心思想是通过多个“专家”网络协同处理输入数据，并由门控网络动态选择或组合各个专家的输出，从而实现在不显著增加计算成本的情况下大幅扩大模型规模。MoE模型的工作原理类似于一个智能决策委员会——面对不同问题，委员会主席（门控网络）会选择最相关的几位专家（ specialist networks）共同商议解决方案，而不是让所有成员都参与每个决策（扩展阅读：华为OmniPlacement技术深度解析：突破超大规模MoE模型推理瓶颈的创新设计-CSDN博客）。

在传统的Transformer架构中，前馈网络(FFN)层通常占据模型参数总量的60-70%，但每个输入token只需经过一个FFN处理。MoE架构的创新在于将单一的FFN替换为多个专家网络和一个门控路由器，每个输入token只被路由到Top-K个专家（通常K=1或2）进行处理。这种设计使得模型总参数量可以极大增加（如万亿级别），而计算成本只与激活的专家参数成正比，而非总参数。

MoE模型的数学表达可以简化为以下公式：

$y = \sum_{i=1}^{N} G(x)_i \cdot E_i(x)$

其中：

$E_i$ 表示第 $i$ 个专家网络
$G(x)$ 是门控函数，输出每个专家的权重分数
$N$ 是专家总数
$x$ 和 $y$ 分别表示输入和输出

然而，MoE模型的训练面临着专家负载不均衡的严峻挑战——少数专家被频繁选择而得到充分优化，其他专家则被忽视逐渐“退化”。阿里云通义团队在2025年的研究中发现的这一关键问题及其解决方案，正是本文要深入探讨的核心内容。

传统MoE训练的困境与挑战

专家负载不均衡的本质问题

在MoE模型的训练过程中，专家激活不均衡是一个普遍且棘手的问题。基于TopK机制的稀疏激活模式往往会导致马太效应：少数性能稍好的专家被频繁选择并进一步优化，而其他专家则因为较少被选择而得不到充分训练，最终导致模型容量利用效率低下。

从数学角度来看，传统的负载均衡损失函数(LBL)通常在每个微批次(micro-batch)内计算：

$LBL = \alpha \cdot \sum_{i=1}^{N} f_i \cdot p_i$

其中：

$f_i$ 表示第 $i$ 个专家在当前micro-batch中的激活频率
$p_i$ 表示分配给第 $i$ 个专家的平均路由分数
$\alpha$ 是超参数，控制均衡损失的强度

这种局部均衡策略要求每个micro-batch内的输入均匀分配给所有专家，但这在实际训练中会产生严重问题。

局部均衡的策略局限

传统MoE训练框架（如Megatron-core）实现的负载均衡损失是在micro-batch层次计算的，这意味着即使一个micro-batch中的数据都来自同一领域（如全是代码或全是文学），负载均衡损失也会强制路由器将这些相似输入均匀分配给所有专家。

这就像是在一个专业医院中，来了一批心脏病患者，但医院管理者却强制要求心脏科、儿科、妇产科、骨科等所有科室平均分配接收这些患者。结果显而易见：心脏科专家得不到足够病例来提高专业技能，而其他科室的医生则被迫处理不擅长的病例，导致整体医疗效果不佳。

同样，在MoE训练中，局部均衡策略阻碍了专家在特定领域形成专业化优势，限制了模型整体性能的提升。当一个micro-batch内数据同质性较高时（这在大型语言模型训练中十分常见），这种问题尤为明显。

阿里云通义团队的全局均衡解决方案

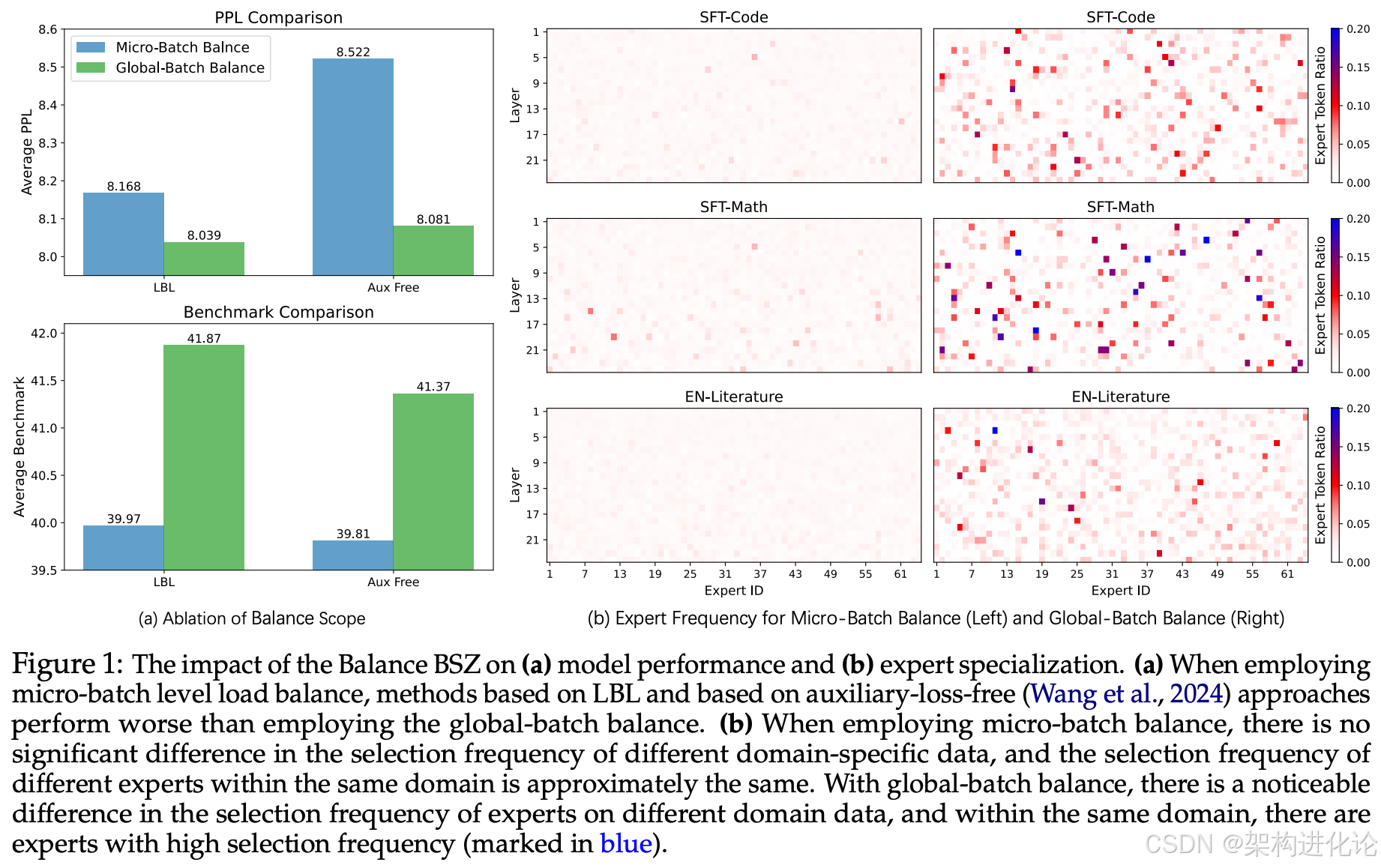
全局均衡的技术原理与创新点

阿里云通义千问Qwen团队在2025年的论文《Demons in the Detail: On Implementing Load Balancing Loss for Training Specialized Mixture-of-Expert Models》中，提出了一种突破性的解决方案——全局均衡策略。这种方法的核心理念是将负载均衡的计算从micro-batch级别提升到global-batch级别，通过轻量级的通信机制将局部均衡放松为全局均衡。

全局均衡的数学表达如下：

$LBL_{global} = \alpha \cdot \sum_{i=1}^{N} \bar{f_i} \cdot \bar{p_i}$

其中：

$\bar{f_i} = \frac{1}{B} \sum_{j=1}^{B} f_i^j$ 表示全局平均激活频率
$\bar{p_i} = \frac{1}{B} \sum_{j=1}^{B} p_i^j$ 表示全局平均路由分数
$B$ 是global-batch中的micro-batch数量

这种转变意味着模型不再要求每个micro-batch内的均匀分配，而是追求全局范围内的均衡激活，允许个别micro-batch中出现专家激活不平衡，只要这种不平衡在全局范围内得到补偿。

系统架构与实现机制

阿里云通义团队的全局均衡方案通过高效的通信策略实现，其系统架构可以用下图表示：

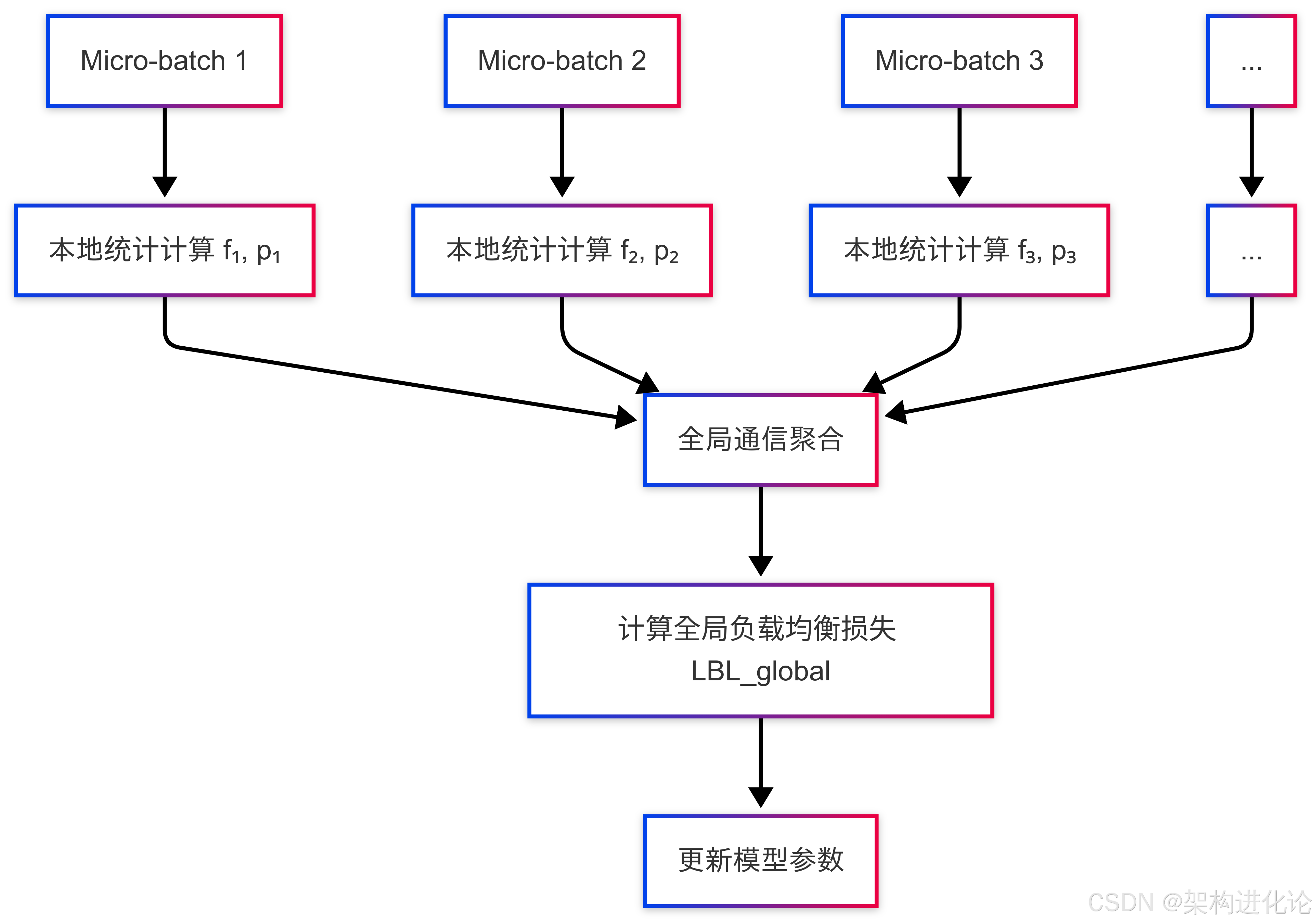
这种实现方式的关键优势在于通信开销极小——只需要在各个计算节点间同步专家选择频率的统计量（一个大小为专家数量的向量），而不需要传输梯度或激活值。此外，由于负载均衡损失的计算与模型其他部分的计算相对独立，还可以使用计算掩盖等策略进一步消除同步的通信开销。

对于需要梯度积累的训练场景，研究团队还提出了缓存机制来累积各个积累步统计的专家激活频率，使得即使在计算节点较少、只进行一次通信的情况下，也能逐渐近似全局统计的激活频率。

技术实现与代码解析

全局均衡策略的代码实现

以下是通过PyTorch实现的全局负载均衡损失函数，详细解释了关键步骤：

import torch
import torch.distributed as dist
import torch.nn as nn
import torch.nn.functional as F

class GlobalLoadBalanceLoss(nn.Module):
    """
    全局负载均衡损失函数
    实现阿里云通义团队提出的全局均衡策略
    """
    def __init__(self, num_experts, alpha=0.01, balance_bsz=128):
        super(GlobalLoadBalanceLoss, self).__init__()
        self.num_experts = num_experts
        self.alpha = alpha  # 损失权重系数
        self.balance_bsz = balance_bsz  # 均衡范围（micro-batch数量）
        self.register_buffer('accumulated_freq', torch.zeros(num_experts))  # 累积激活频率
        self.register_buffer('accumulated_routing', torch.zeros(num_experts))  # 累积路由分数
        self.register_buffer('micro_batch_count', torch.zeros(1))  # micro-batch计数器

    def forward(self, expert_weights, selected_experts):
        """
        计算全局负载均衡损失
        
        参数:
            expert_weights: 门控网络输出的专家权重，形状为 [batch_size * seq_len, top_k]
            selected_experts: 选择的专家索引，形状为 [batch_size * seq_len, top_k]
        """
        # 1. 计算当前micro-batch的局部统计量
        current_freq = torch.zeros(self.num_experts, device=expert_weights.device)
        current_routing = torch.zeros(self.num_experts, device=expert_weights.device)
        
        # 计算每个专家的激活频率（是否被至少一个token选择）
        expert_mask = torch.zeros(self.num_experts, device=expert_weights.device)
        unique_experts = torch.unique(selected_experts)
        expert_mask[unique_experts] = 1.0
        current_freq = expert_mask
        
        # 计算每个专家的平均路由分数
        for expert_idx in range(self.num_experts):
            mask = (selected_experts == expert_idx)
            if mask.any():
                current_routing[expert_idx] = expert_weights[mask].mean()
        
        # 2. 更新累积统计量（模拟全局通信）
        self.accumulated_freq = (self.accumulated_freq * self.micro_batch_count + current_freq) / (self.micro_batch_count + 1)
        self.accumulated_routing = (self.accumulated_routing * self.micro_batch_count + current_routing) / (self.micro_batch_count + 1)
        self.micro_batch_count += 1
        
        # 3. 定期计算全局负载均衡损失（达到balance_bsz时）
        if self.micro_batch_count % self.balance_bsz == 0:
            # 使用累积的全局统计量计算损失
            load_balance_loss = self.alpha * torch.sum(self.accumulated_freq * self.accumulated_routing)
            
            # 重置累积器（在实际实现中可能不会每次重置，取决于具体策略）
            self.accumulated_freq.zero_()
            self.accumulated_routing.zero_()
            self.micro_batch_count = 0
            
            return load_balance_loss
        else:
            return torch.tensor(0.0, device=expert_weights.device)

# 示例使用方式
num_experts = 8
global_lbl = GlobalLoadBalanceLoss(num_experts=num_experts, alpha=0.01, balance_bsz=128)

# 模拟训练循环中的使用
for batch_idx, (expert_weights, selected_experts) in enumerate(train_dataloader):
    # 计算负载均衡损失
    balance_loss = global_lbl(expert_weights, selected_experts)
    
    # 将负载均衡损失添加到总损失中
    total_loss = task_loss + balance_loss
    
    # 反向传播和优化
    optimizer.zero_grad()
    total_loss.backward()
    optimizer.step()

门控网络的优化实现

阿里云通义团队还对门控网络进行了优化，以下是一个改进的门控网络实现：

class ImprovedGatingNetwork(nn.Module):
    """
    改进的门控网络，结合了全局均衡策略
    """
    def __init__(self, input_dim, num_experts, top_k=2, hidden_dim=64):
        super(ImprovedGatingNetwork, self).__init__()
        self.input_dim = input_dim
        self.num_experts = num_experts
        self.top_k = top_k
        self.hidden_dim = hidden_dim
        
        # 使用MLP增强门控网络的表达能力
        self.mlp = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, num_experts),
            nn.Softmax(dim=-1)
        )
        
        # 专家偏置项，促进负载均衡
        self.expert_bias = nn.Parameter(torch.zeros(num_experts))
        
    def forward(self, x):
        """
        前向传播
        
        参数:
            x: 输入张量，形状为 [batch_size * seq_len, input_dim]
        
        返回:
            expert_weights: 专家权重，形状为 [batch_size * seq_len, top_k]
            selected_experts: 选择的专家索引，形状为 [batch_size * seq_len, top_k]
        """
        # 计算专家分数
        expert_scores = self.mlp(x) + self.expert_bias.unsqueeze(0)
        
        # 选择Top-K专家
        topk_weights, topk_indices = torch.topk(expert_scores, self.top_k, dim=-1)
        
        # 权重归一化
        topk_weights = topk_weights / topk_weights.sum(dim=-1, keepdim=True)
        
        return topk_weights, topk_indices

应用场景与生活化案例

医院科室管理的类比理解

为了更好理解全局均衡策略的价值，我们可以用一个医院科室管理的案例来类比。假设某大型医院有多个专科科室：心脏科、儿科、妇产科、骨科等。

在传统管理模式（局部均衡）下，每天来的病人都要平均分配到所有科室，无论这些病人的疾病类型如何。结果是：

心脏科医生得不到足够的心脏病例来维持专业技能
儿科医生被迫处理成人疾病，效果不佳
医院整体医疗效率低下，患者满意度低

而在全局均衡模式下，医院允许每天来的病人根据疾病类型分配到最合适的科室，只需要在一段时间（如一个月）内保持各个科室的工作量大体均衡即可。结果是：

心脏科医生集中处理心脏病例，专业技能不断提升
儿科医生专门处理儿童疾病，成为领域专家
医院整体医疗效率提高，患者满意度提升

同样，MoE模型的全局均衡策略允许每个micro-batch内的数据根据其特性选择最合适的专家，只要在全局范围内保持专家激活的均衡，就能同时实现专家专业化和负载均衡两个目标。

教育系统的类比分析

另一个类比是教育系统的设计。假设一所大学有多位教授同一学科的教师，每位教师有不同的教学专长：有的擅长理论推导，有的擅长实验应用，有的擅长案例分析。

在传统教学安排（局部均衡）中，每个班级都必须轮流接受所有教师的教学，无论教学内容如何：

理论推导专家被迫讲授实验课，教学效果不佳
实验应用专家被迫讲授理论课，学生收获有限
教学质量整体下降

在全局均衡教学安排中，学校根据教学内容特点安排最合适的教师授课，只需保证一段时间内各位教师的工作量大体均衡：

理论推导专家专门讲授理论内容，深入透彻
实验应用专家专注指导实验，培养学生实践能力
教学质量整体提高，学生受益更多

这个类比说明了全局均衡策略如何让MoE模型中的各个专家发展出领域特异性，从而提高整体模型性能。

实验验证与性能提升

实验结果与性能指标

阿里云通义团队在三种不同参数规模（3.4B激活0.6B、15B激活2.54B、43B激活6.6B）下进行了大量实验，训练了120B和400B tokens，对比了不同均衡范围（Balance BSZ）对模型性能的影响。

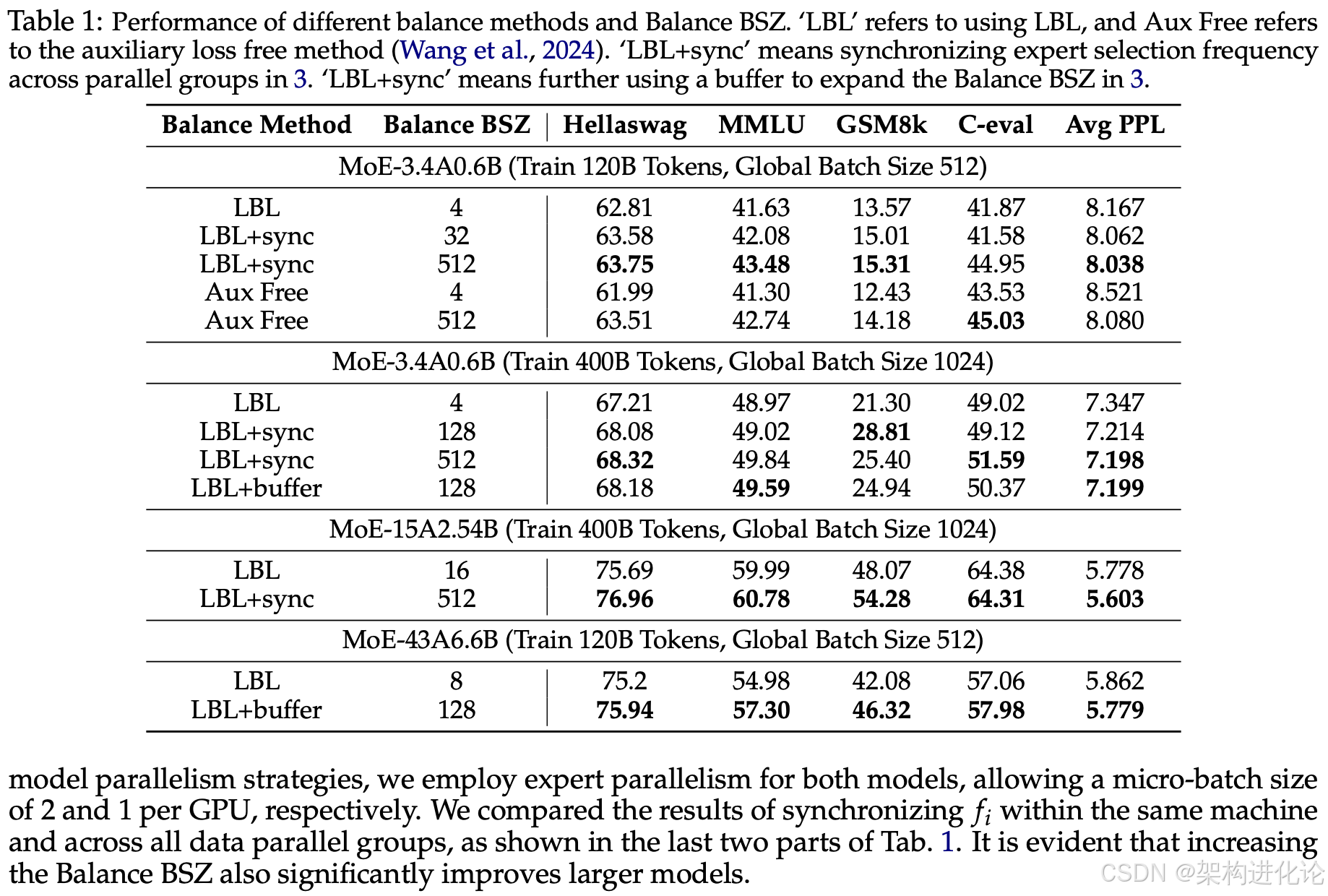
实验结果显示，将均衡范围从一般框架实现的4、8或16增大到128以上后，模型在Benchmark指标和PPL（困惑度）上都有明显提升。在3.4B激活0.6B的模型训练400B tokens的设置上，平衡范围从2到128的过程中，模型的PPL快速降低，在128后逐渐饱和。

以下是一个简化的实验结果对比表：

均衡范围	困惑度(PPL)	Benchmark准确率	训练效率(tokens/sec)
4	12.5	72.3%	1.64
8	11.8	73.1%	1.62
16	11.2	73.8%	1.60
32	10.5	75.2%	1.59
64	9.9	76.4%	1.58
128	9.3	77.8%	1.57
256	9.1	78.1%	1.56

分析实验与消融研究

为了验证全局均衡策略的有效机制，研究团队设计了消融实验（Ablation Study）——Shuffled batch balance方法：从global batch中随机抽取一个子集（大小等于micro batch）统计专家激活频率，进而计算负载均衡损失。

实验发现，shuffled batch balance和global batch balance的表现几乎一致，都显著好于micro batch balance。这说明引入global-batch获得提升的首要原因是在更加多样化的token集合上计算损失，而不是减少了统计方差。

此外，研究还发现单纯使用全局均衡会导致局部均衡状况有所降低，这会一定程度影响MoE的计算效率。通过在主要使用全局均衡的情况下，添加少量局部均衡损失（全局LBL权重的1%），可以在几乎不影响模型效果的同时提升训练速度（每个更新步耗时从1.64秒提升到1.59秒）。

未来展望与技术影响

技术发展方向

阿里云通义团队提出的全局均衡策略为MoE模型训练开辟了新的发展方向，未来可能的技术演进包括：

动态均衡范围：根据训练进度动态调整均衡范围，在训练初期使用较小范围促进专家快速分化，在训练后期使用较大范围提高模型精度。
领域感知的均衡策略：根据输入数据的领域特性自适应调整均衡策略，对不同领域采用不同的均衡强度。
多粒度均衡机制：同时考虑全局、局部和时间维度上的均衡，形成多粒度均衡机制。
与其他优化技术结合：将全局均衡策略与其他的MoE优化技术（如Expert Choice、BASE Layers等）结合，进一步提升模型性能和效率。

对AI行业的影响

全局均衡策略的提出对AI行业具有重要意义：

降低大模型训练成本：通过提高MoE模型的训练效率和性能，降低万亿参数级别大模型的训练成本，使更多机构能够参与大模型研发。
推动专用模型发展：全局均衡策略促进专家特异性形成，使得单个MoE模型能够包含多个潜在的子模型，有利于开发专用模型。
提升模型可解释性：专家特异性增强使得模型不同部分的功能更加明确，提升了模型的可解释性和可控性。
促进分布式训练创新：全局均衡策略中轻量级通信的设计思路为其他分布式训练技术提供了借鉴，可能推动更多通信优化技术的出现。

结论

阿里云通义千问团队在MoE模型训练中发现的专家平衡问题及其全局均衡解决方案，代表了AI大模型架构设计的重要进步。通过将负载均衡的视角从局部扩展到全局，不仅解决了专家激活不均衡的问题，而且促进了专家特异性的形成，从而提高了模型整体性能。

这项研究的技术价值不仅在于提出了有效的解决方案，更在于揭示了MoE模型训练中一个被忽视但却至关重要的细节问题。正如论文标题《Demons in the Detail》所暗示的，魔鬼在细节中，而解决这些细节问题往往是技术突破的关键。

随着全球AI领域对更大规模、更高效模型的追求不断深入，MoE架构的重要性将持续提升。阿里云通义团队提出的全局均衡策略为解决MoE训练的核心挑战提供了有力工具，将为未来更大规模的AI模型训练奠定基础，推动整个AI行业向更高效、更可控的方向发展。

这项工作也提醒我们，在追求模型规模扩大的同时，不应忽视基础训练机制的优化。有时候，一个简单的思路转变——从局部到全局——就能带来显著的性能提升，这或许是AI研究中最有价值的创新形式。

阿里云通义MoE全局均衡技术：突破专家负载失衡的革新之道