数据结构之二叉树（3）

1.向上调整算法建堆的时间复杂度

//向上调整
void AdjustUp(HpDataType* arr, int child) {
	int parent = (child - 1) / 2;
	while (child > 0) {
		if (arr[child] > arr[parent]) {
			Swap(&arr[child], &arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else {
			break;
		}
	}
}
//入堆
void HpPush(Hp* php,HpDataType x) {
	assert(php);
	//空间不够增容
	if (php->size == php->capacity) {
		int newcapacity = php->capacity == 0 ? 4 : 2 * (php->capacity);
		HpDataType* tmp = (HpDataType*)realloc(php->arr, newcapacity * sizeof(HpDataType));
		if (tmp == NULL) {
			perror("realloc fail");
			exit(1);
		}
		php->arr = tmp;
		php->capacity = newcapacity;
	}
	php->arr[php->size++] = x;
	//向上调整
	AdjustUp(php->arr, php->size - 1);
}

堆是完全二叉树，所以我们近似使用满二叉树来证：

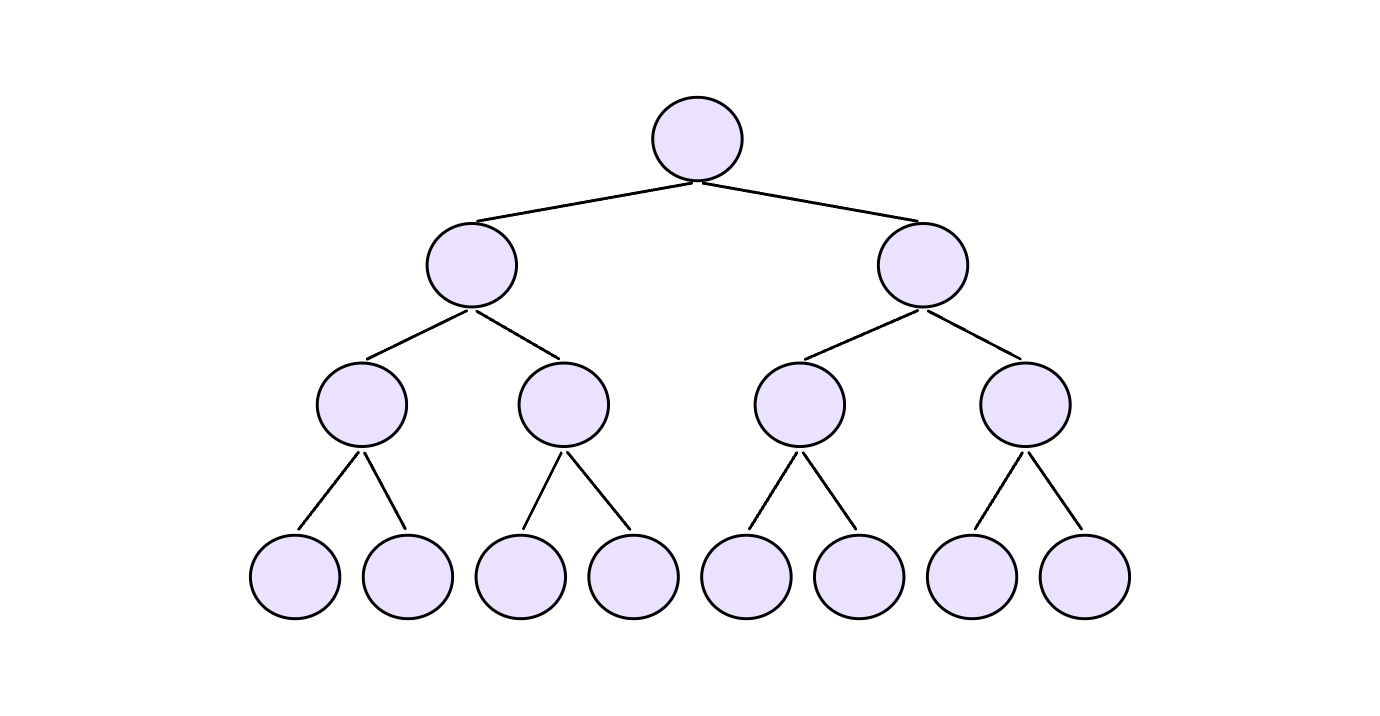
假设每一个结点入堆都需要向上调整至堆顶，那么：
第1层，2^0个结点，需要向上移动0层
第2层，2^1个结点，需要向上移动1层
第3层，2^2个结点，需要向上移动2层
第4层，2^3个结点，需要向上移动3层
…
第h层，2^(h-1)个结点，需要向上移动h-1层
把它们都相加起来：

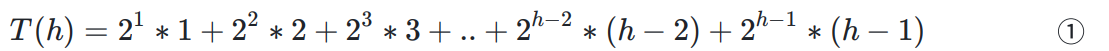
我们使用高中做数列题的功底：×2

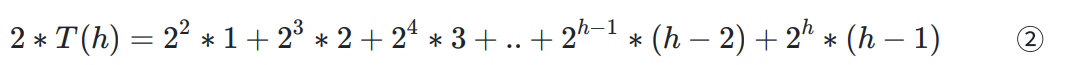
二式减一式，得


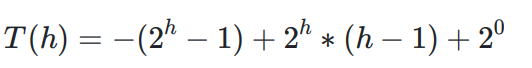
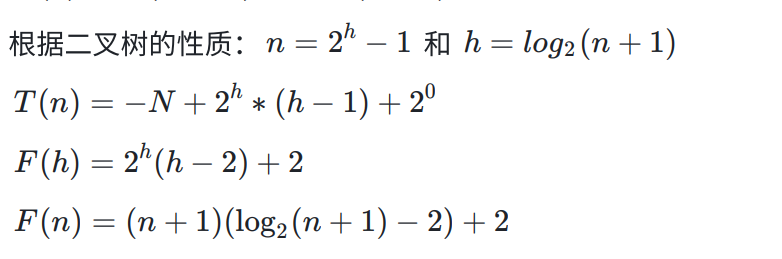
所以，向上调整算法建堆时间复杂度为；O(n*log2n).

2.向下调整算法建堆的时间复杂度

//向下调整
void AdjustDown(HpDataType* arr, int parent, int n) {
	int child = 2 * parent + 1;
	while (child < n) {
		if (child + 1 < n && arr[child] < arr[child + 1]) {
			child++;
		}
		if (arr[child] > arr[parent]) {
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else {
			break;
		}
	}
}
//入堆
void HpPush(Hp* php,HpDataType x) {
	assert(php);
	//空间不够增容
	if (php->size == php->capacity) {
		int newcapacity = php->capacity == 0 ? 4 : 2 * (php->capacity);
		HpDataType* tmp = (HpDataType*)realloc(php->arr, newcapacity * sizeof(HpDataType));
		if (tmp == NULL) {
			perror("realloc fail");
			exit(1);
		}
		php->arr = tmp;
		php->capacity = newcapacity;
	}
	php->arr[php->size++] = x;
	//向下调整
	AdjustDown(php->arr, 0，php->size);
}

同理：
第1层，2^0个结点，需要向下移动h-1层
第2层，2^1个结点，需要向上移动h-2层
第3层，2^2个结点，需要向上移动h-3层
第4层，2^3个结点，需要向上移动h-4层
…
第h层，2^(h-1)个结点，需要向上移动0层


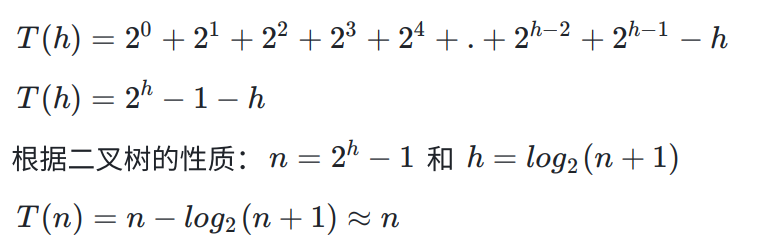
所以，向下调整算法建堆的时间复杂度为O(n).

3.堆排序（Heap Sort）

给出一个无序的数组，先把它建堆。
从最后一个父节点开始，向下调整，之后每次i–使得所有结点都能被遍历到。

//建立堆结构,n为结点个数
for (int i = (n - 1 - 1) / 2; i >= 0;i--) {
	AdjustDown(arr, i, n);
}

到这里已经把数组的第一个元素变成最大的，每次取出堆顶然后与最后一个元素交换，再向下调整，使其在变成一个堆

int end = n - 1;
while (end > 0) {
	int top = arr[0];
	Swap(&arr[end], &arr[0]);
	AdjustDown(arr, 0, end);
	end--;
}
for (int i = 0;i < n;i++) {
	printf("%d ", arr[i]);
}

在向上（下）调整算法中，改变>号或<号就可以改为升序或降序。

//堆排序
void HeapSort(int* arr,int n) {
	//建立堆结构
	for (int i = (n - 1 - 1) / 2; i >= 0;i--) {
		AdjustDown(arr, i, n);
	}
	//到这里已经把数组的第一个元素变成最大的
	//每次取出堆顶然后与最后一个元素交换，再向下调整，使其在变成一个堆
	int end = n - 1;
	while (end > 0) {
		int top = arr[0];
		Swap(&arr[end], &arr[0]);
		AdjustDown(arr, 0, end);
		end--;
	}
	for (int i = 0;i < n;i++) {
		printf("%d ", arr[i]);
	}
}

完
如果发现错误，欢迎打在评论区。
主页还有更多优质内容OvO