ICCV 2025|基于曲线感知高斯溅射的3D参数曲线重建

论文信息

题目：Curve-Aware Gaussian Splatting for 3D Parametric Curve Reconstruction

基于曲线感知高斯溅射的3D参数曲线重建

作者：Zhirui Gao, Renjiao Yi, Yaqiao Dai, Xuening Zhu, Wei Chen, Chenyang Zhu, Kai Xu

论文创新点

1. 提出单阶段优化框架：论文提出一种端到端的单阶段优化框架，直接从多视图边缘图中优化3D参数曲线，避免了传统两阶段方法（“边缘点云重建+参数曲线拟合”）中因阶段分离导致的误差累积问题，有效提升重建精度。
2. 设计双向耦合机制：设计了一种参数曲线与面向边缘的高斯分量之间的双向耦合机制，构建了曲线感知高斯表示（CurveGaussian）。通过这种紧密对应关系，实现3D曲线的可微渲染，使得参数曲线能在多视图信息的引导下直接优化，同时显著减少优化所需参数数量。
3. 采用动态拓扑优化策略：引入动态自适应拓扑优化框架，在训练过程中通过线性化、合并、拆分和修剪等操作对曲线结构进行细化。
4. 优化损失函数：设计多目标损失函数，包括边缘感知渲染损失、平滑连接正则化、平滑曲线正则化和简洁曲线正则化等项。

摘要

本文提出了一种端到端的框架，可直接从多视图边缘图重建3D参数曲线。与现有的两阶段方法不同，后者采用“边缘点云重建与参数曲线拟合”的顺序流程，而作者的单阶段方法直接从2D边缘图优化3D参数曲线，消除了因不连续阶段之间固有的优化差距而导致的误差累积。然而，参数曲线本质上不太适合基于渲染的多视图优化，因此需要一种互补的表示方式，既能保留其几何特性，又能实现可微渲染。作者提出了一种新颖的参数曲线与面向边缘的高斯分量之间的双向耦合机制。这种紧密的对应关系构建了一种曲线感知高斯表示（CurveGaussian），能够对3D曲线进行可微渲染，从而可以在多视图证据的指导下直接进行优化。此外，作者在训练过程中引入了一个动态自适应拓扑优化框架，通过线性化、合并、拆分和修剪操作来细化曲线结构。在ABC数据集和真实世界基准测试中的综合评估表明，作者的单阶段方法优于两阶段方法，特别是在生成更清晰、更稳健的重建结果方面。此外，通过直接优化参数曲线，该方法在训练过程中显著减少了参数数量，与现有方法相比，实现了更高的效率和更优越的性能。

关键词

3D参数曲线重建；多视图边缘图；可微渲染；高斯溅射；动态拓扑优化

一、引言

参数曲线作为基本的几何图元，在结构化3D表示和几何理解中起着至关重要的作用。它们在保持与CAD兼容性的同时压缩几何信息的能力，使其在工业应用中不可或缺。一个关键挑战在于从非结构化数据（如含噪点云或多视图图像）中重建高精度参数曲线，因为传感器的不完美和不完整观测不可避免地会降低重建质量。

传统的3D曲线重建方法通常需要干净的3D点云作为输入，以便后续进行拟合过程。最近的NEF框架首次通过“边缘点云重建 + 参数曲线拟合”的两阶段流程，将神经辐射场与基于RANSAC的优化相结合，直接从2D图像实现了3D曲线重建。然而，这种方法在不连续的两阶段优化过程中会累积误差，使其对重建点云的噪声敏感。EMAP通过无偏距离UDF建模和消除方程渲染来增强边缘定位，对NEF进行了改进。尽管其“先聚类后拟合”策略减少了误差传播，但该方法从根本上仍然受到第一阶段给定的点云质量的限制。值得注意的是，由于每个阶段都要进行独立的神经优化，这些方法的计算效率较低。虽然EdgeGaussians使用高斯溅射加速了重建，但它仍然无法克服两阶段流程固有的局限性。

两阶段范式存在两个基本限制。首先，参数拟合过程与观测噪声/误差紧密耦合，这些噪声通过多视图三角测量从2D边缘检测传播到3D点云，导致最终曲线出现冗余分支或断裂（如图1所示）。其次，贪婪迭代拟合（例如RANSAC）会产生局部最优解累积，导致曲线冗余随着场景复杂性呈指数增长，这严重影响了下游应用效率。消除阶段之间的优化差距成为稳健重建的关键。

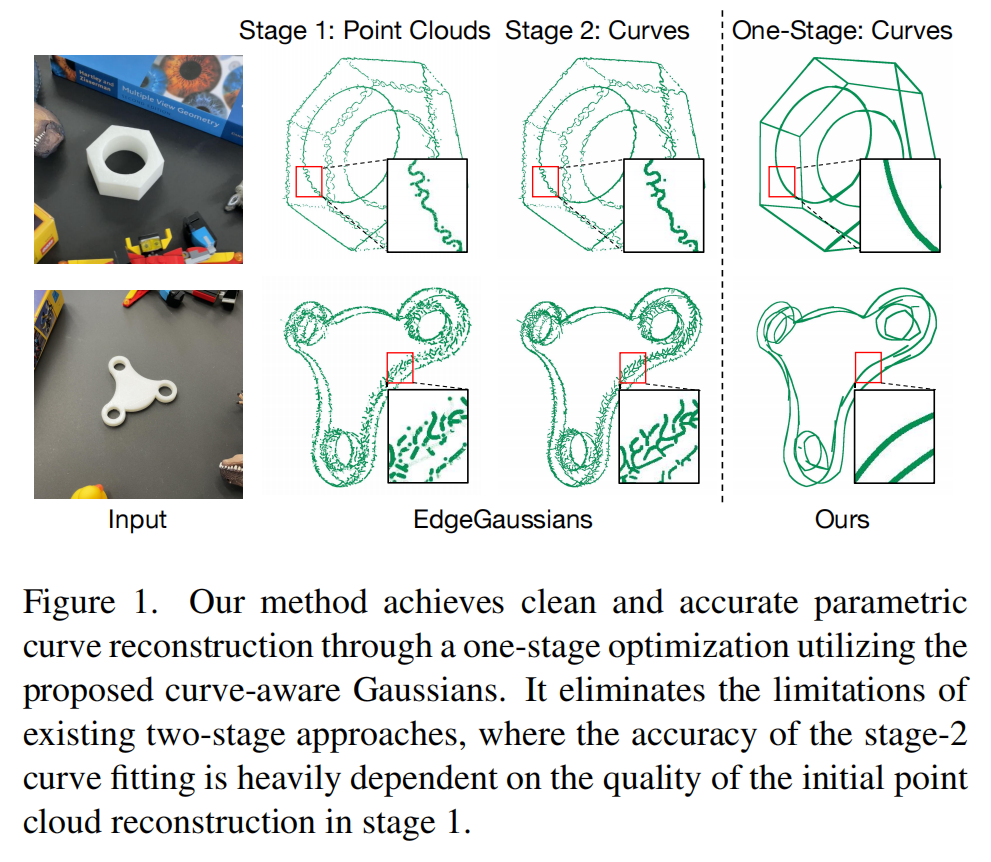
虽然2D边缘图更容易获取，但绕过显式的3D边缘点云重建是解决此问题的一种有前途的方法。直接的单阶段曲线优化面临两个基本挑战：参数表示本质上缺乏可微渲染能力，而神经渲染框架（NeRF/高斯）在逼近曲线时无法保持几何连续性。作者提出了一种混合神经表示，即CurveGaussians，它将参数曲线与面向边缘的高斯分量相结合。通过建立双向耦合，每个贝塞尔曲线段精确控制其相关高斯分量的空间分布。这使得通过溅射实现可微渲染，同时显著减少优化所需的参数数量。

基于这种混合表示，本文提出了一种从多视图边缘图重建参数曲线的单阶段方法。其核心概念是绕过中间点云表示，直接对贝塞尔曲线的控制点进行可微优化，其中每条曲线由多个面向边缘的高斯组成。具体来说，每个高斯分量与相应曲线的特定边缘段相关联，其位置和方向属性从曲线参数中解析得出。渲染损失通过反向传播来更新曲线控制点，从而能够同时利用神经渲染的光度一致性约束和参数曲线的内在几何正则化。为了在训练过程中进一步优化曲线拓扑，以实现更清晰、更紧凑的重建，作者提出了一种动态拓扑优化策略，通过合并、拆分和修剪操作自适应地细化边缘结构。此外，作者改进了优化损失，以优先考虑生成曲线的结构紧凑性。实验结果表明，与两阶段的SOTA方法相比，作者的单阶段方法在重建精度上提高了14.5%，计算效率提高了33%，生成的曲线数量减少了70.5%，实现了更准确、更紧凑的重建。总之，本文的贡献包括：

• 提出了一种新颖的参数曲线与面向边缘的高斯分量之间的双向耦合框架，通过可微高斯溅射实现参数曲线的直接优化。
• 提出了一种训练时的结构细化策略，自适应地优化曲线拓扑，实现紧凑的参数曲线重建。
• 与现有的两阶段方法相比，作者的单阶段优化框架对重建噪声具有更强的鲁棒性，在实际场景中显著提高了精度。

三、方法

大多数从多视图边缘图像重建参数化3D曲线的现有方法通常遵循两阶段方法：重建3D边缘表示（例如，使用NeRF、UDF或3DGS）以获得边缘点云，然后拟合参数曲线。虽然这种方法在概念上很简单，但它存在关键限制。两阶段范式会导致误差累积。由于曲线拟合在很大程度上依赖于点云重建的准确性，第一阶段的任何噪声都会显著降低最终的参数曲线质量。这些问题也会导致效率降低。为了解决这些限制，作者提出了一种单阶段优化方法，通过所提出的曲线感知高斯溅射直接优化参数曲线，如图2所示。

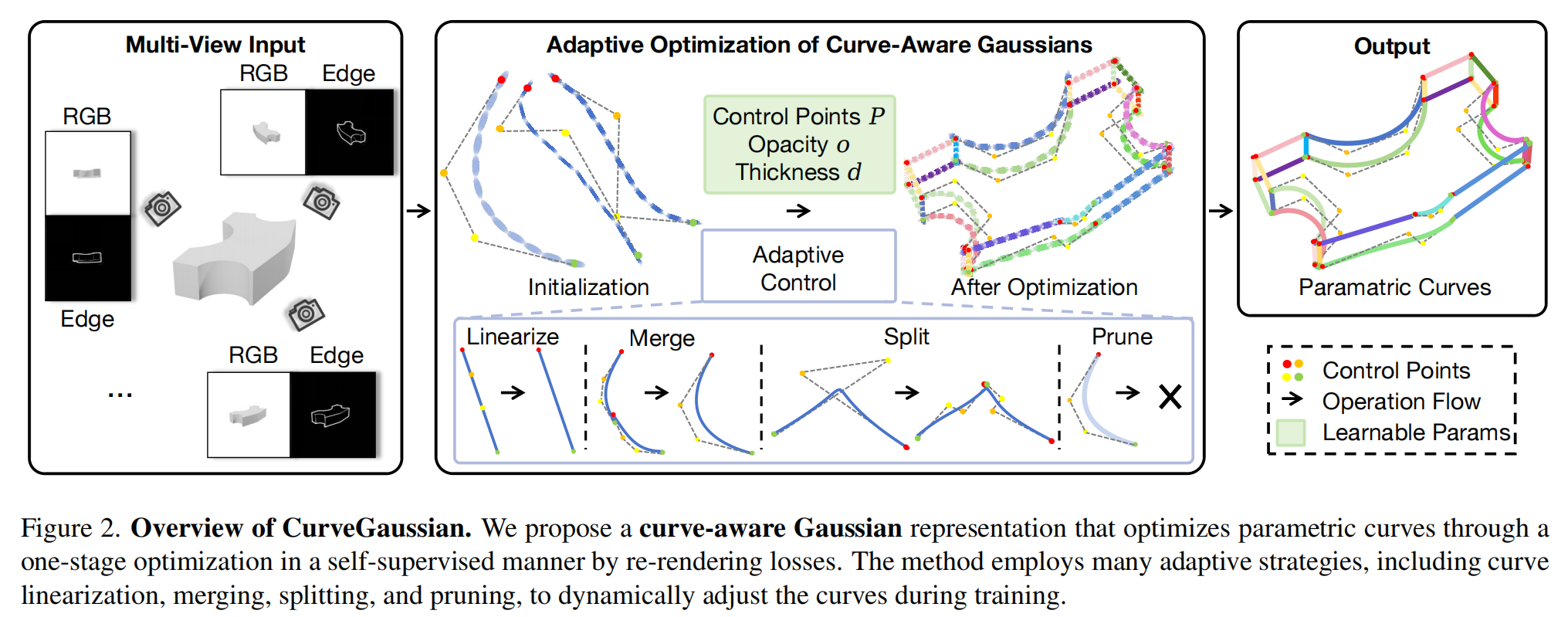
作者首先在3.1节中对问题进行形式化定义，随后在3.2节中介绍曲线感知高斯溅射框架，该框架能够直接渲染参数曲线。然后在3.3节和3.4节中介绍自适应优化，旨在在训练过程中稳定学习复杂的曲线拓扑。

3.1问题定义

参数曲线重建的任务旨在从多视图2D边缘图中恢复3D参数曲线。正式地，给定一组参数曲线{Cj}\{C_j\}{Cj​}，其中$C_j$表示第$j$条曲线，作者优化它们的参数（例如，控制点），使得它们渲染出的2D投影与所有视图中观察到的边缘图像对齐。它被表述为以下优化问题：
arg min{Cj}∑k=0K−1∑j=0C−1Lr(f({Cj},Tk),I^k). \underset{\{C_j\}}{\text{arg min}} \sum_{k = 0}^{K - 1} \sum_{j = 0}^{C - 1} \mathcal{L}_r \left( f(\{C_j\}, \mathbf{T}_k), \hat{I}_k \right). {Cj​}arg min​k=0∑K−1​j=0∑C−1​Lr​(f({Cj​},Tk​),I^k​).
这里，${\mathbf{T}}_k$表示第$k$个视图的相机姿态，${\hat{I}}_k$是视图$k$的真实边缘图，$f(\cdot )$是将参数曲线映射到边缘图的渲染函数，${\mathcal{L}}_r$是渲染损失。$K$和$C$分别表示观察视图的数量和曲线的总数。

通过利用可微渲染函数$f(\cdot )$，作者的方法将曲线重建与多视图边缘图像紧密耦合，并直接优化参数曲线，强制局部边缘一致性。它避免了两阶段过程中的误差累积和低效率问题。此外，直接优化曲线参数减少了优化变量的数量并提高了计算效率，如表2所示。

参数曲线：在该框架中，作者将每条曲线$C_j$表示为参数曲线$c_j(t)$，其中$t\in [0,1]$对曲线从起点（$t=0$）到终点（$t=1$）进行参数化。作者使用两种类型的参数曲线：三次和一阶贝塞尔曲线，它们足以描述大多数场景中遇到的大多数形状。

三次贝塞尔曲线：三次贝塞尔曲线由四个控制点定义：$P_0^j$（起点），$P_1^j$，$P_2^j$和$P_3^j$（终点）。曲线参数化为：
$$c_j(t)=\sum _{k=0}^3{B}_k^3(t)P_k^j,$$
其中$B_k^3(t)=\left(\genfrac{}{}{0ex}{}{3}{k}\right)t^k(1-t{)}^{3-k}$是伯恩斯坦基函数。控制点决定了曲线的形状，允许进行平滑且灵活的表示。

一阶贝塞尔曲线（线段）：一阶贝塞尔曲线（线段）由其两个端点$P_0^j$和$P_1^j$定义，参数化为：
$$c_j(t)=(1-t)P_0^j+t{P}_1^j.$$
一阶贝塞尔曲线比三次贝塞尔曲线简单，但对于表示直线段很有用。

为了更好地在3D空间中表示曲线，确保与高斯表示的兼容性，并增强曲线的表现力，每条曲线都与两个额外参数相关联：不透明度$o_j\in [0,1]$，它控制第$j$条曲线的可见性，以及厚度$d_j\in {\mathbb{R}}^{+}$，它决定曲线的宽度。

3.2曲线感知高斯溅射

关键挑战在于设计一个可微渲染函数$f(\cdot )$。为了实现这一点，作者提出了一种将参数曲线与高斯基元相结合的混合表示。作者在参数曲线和高斯之间建立双向耦合，其中每条曲线$c_j$通过均匀采样生成$N$（$N=12$）个高斯，如图2所示。高斯属性由曲线几何形状决定：
位置与方向：$c_j$中的第$i$个高斯$G_i^j$锚定在曲线点$p_j(t_i)$处，其中$t_i=\frac{i+0.5}{N}$，i∈{0,1,…,N−1}i \in \{0, 1, \ldots, N - 1\}i∈{0,1,…,N−1}。$p_j(t_i)$的主轴$v_0$与曲线切线${\mathbf{T}}_j(t_i)$对齐。第二轴$v_1$调整为与$v_0$垂直，第三轴$v_2$作为$v_0$和$v_1$的叉积获得，确保在3D空间中的正交性。
尺度与不透明度：轴向尺度定义为：${\mathbf{s}}_{j,i}={\left[\Vert \Delta {\mathbf{p}}_i^j\Vert ,d_j,d_j\right]}^{\top }$，其中$\Delta {\mathbf{p}}_i^j=p_j(t_{i+1})-p_j(t_i)$，$d_j$表示特定于曲线的厚度参数。在实践中，主轴的尺度明显大于其他轴，从而产生杆状且面向边缘的高斯。高斯的不透明度$o_i^j$继承自父曲线的属性$o_j$。
掩码：为了解决重叠区域的冗余和非边缘区域可能的过度覆盖问题，作者按照[11]为每个高斯引入一个可学习的重要性掩码$m_{j,i}\in [0,1]$。该掩码在优化过程中作为一种门控机制，这意味着当$m_{j,i}$接近0时，$G_i^j$会被有效地抑制。此属性通过梯度驱动的掩码衰减自动指示沿曲线段的冗余或位置不当的高斯。

结果，公式1中的渲染函数$f(\cdot )$可以通过曲线感知高斯溅射来实现。溅射遵循标准的3D高斯溅射（3DGS）管道，但去除颜色属性，因为边缘图是单通道的。相反，直接使用alpha加权值来计算渲染图像和渲染损失。

3.3曲线感知高斯的自适应控制

在缺乏曲线数量或位置的先验知识的情况下，作者用随机贝塞尔参数化曲线初始化该过程。这种方法导致优化过程与原始3DGS显著不同。具体来说，高斯基元的数量动态演变，从一个大集合开始，在优化过程中逐渐减少到一个更小、更精细的集合。这种行为需要一种自适应策略，以确保稳定和准确的结果。如图2底部所示，采用了四种自适应策略，详细内容如下：

曲线线性化策略：在训练过程中，如果三次贝塞尔曲线接近直线，则将其转换为一阶贝塞尔曲线（线段）。具体来说，通过对三次贝塞尔曲线$c_j(t)$进行均匀采样，作者获得一组点{pi}i=1N\{\mathbf{p}_i\}_{i = 1}^N{pi​}i=1N​，然后拟合一条直线。如果满足以下条件，则曲线$c_j(t)$被线段$c_j^{\prime }(t)$取代：
$$c_j^{\prime }(t)=(1-t)P_0^j+t{P}_3^j,\text{如果}\frac{1}{N}\sum _{i=1}^N{\Vert c_j^{\prime }(t_i)-{\mathbf{p}}_i\Vert }^2<{\tau }_l,$$
其中${\tau }_l$是预定义的误差阈值，$P_0^j$和$P_3^j$是三次贝塞尔曲线$c_j(t)$的起点和终点，$t\in [0,1]$。这种转换在保持曲线几何表示的同时降低了计算复杂度。

曲线合并策略：

直线合并：对于两条线段$c_1(t)$和$c_2(t)$，计算它们方向之间的角度$\theta$以及它们最近端点之间的空间距离$d$。如果$\theta <{\tau }_{la}$且$d<{\tau }_{ld}$，则将这两条线合并，其中${\tau }_{la}$和${\tau }_{ld}$是预定义的角度和空间阈值。

三次贝塞尔曲线合并：对于两条相邻的贝塞尔曲线$c_1(t)$和$c_2(t)$，通过从两条曲线中采样得到的一组点{pi}i=1N\{\mathbf{p}_i\}_{i = 1}^N{pi​}i=1N​拟合一条新的贝塞尔曲线$c^{\prime }(t)$。如果$\frac{1}{N}{\sum }_{i=1}^N{\Vert c^{\prime }(t_i)-{\mathbf{p}}_i\Vert }^2<{\tau }_b$，则将这两条曲线合并并替换为$c^{\prime }(t)$，其中${\tau }_b$是预定义的误差阈值。

这种策略不仅简化了曲线的表示，还确保它们紧凑，保持几何精度，非常适合高效的曲线感知高斯溅射。

曲线拆分策略：具有控制点$P_{0,0}^j$，$P_{1,0}^j$，$P_{2,0}^j$，$P_{3,0}^j$的三次贝塞尔曲线$c_j(t)$，可以在$t=s$处使用德卡斯特里奥算法拆分为两条子曲线：
c1:{P0,0j,P0,1j,P0,2j,P0,3j}c2:{P0,3j,P1,2j,P2,1j,P3,0j}, c_1 : \{ P^j_{0, 0}, P^j_{0, 1}, P^j_{0, 2}, P^j_{0, 3} \} \\ c_2 : \{ P^j_{0, 3}, P^j_{1, 2}, P^j_{2, 1}, P^j_{3, 0} \}, c1​:{P0,0j​,P0,1j​,P0,2j​,P0,3j​}c2​:{P0,3j​,P1,2j​,P2,1j​,P3,0j​},
中间控制点通过递归计算：
$$P_{i,k}^j=(1-s)P_{i,k-1}^j+s{P}_{i+1,k-1}^j.$$
如图3所示，在两种情况下触发拆分操作：

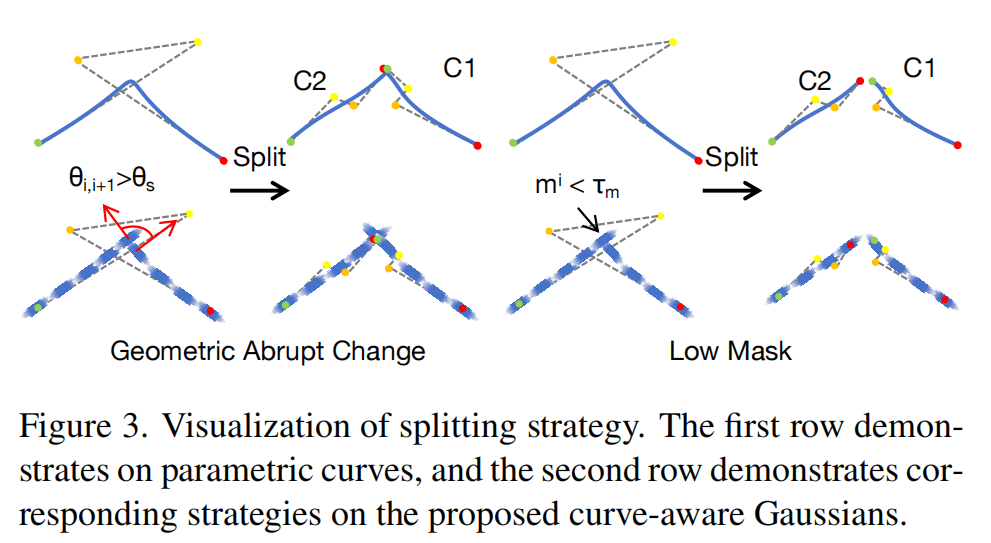
几何突变检测：通过计算曲线上相邻高斯主轴之间的角度${\theta }_{i,i+1}=\arccos ({\mathbf{v}}_{j,i}^1\cdot {\mathbf{v}}_{j,i+1}^1)$来检测局部几何突变。如果${\max }_i{\theta }_{i,i+1}>{\theta }_s$，则将最大突变点定位为$t^{\ast }={\text{arg max}}_t\theta (t)$，并直接在$t^{\ast }$处拆分曲线以获得两条新曲线$c_1$和$c_2$。

低掩码检测：如果曲线上掩码最小的高斯满足$m_i^j<{\tau }_m$，则在$t_{i-1}$处拆分曲线保留$c_1$，在$t_{i+1}$处拆分保留$c_2$，并移除该高斯点。

这种策略确保曲线在消除冗余段的同时保持平滑。

曲线修剪策略：如果$o_j<{\tau }_d$，则动态移除曲线$c_j(t)$，其中$o_j$表示第$j$条曲线的不透明度，${\tau }_d$是预定义的阈值。如果曲线上所有高斯的掩码都小于${\tau }_m$，则也将移除该曲线。这种策略确保移除基本透明的曲线，从而提高表示的整体质量。

3.4优化曲线感知高斯

作者通过以下多目标损失来优化曲线参数{Pkj,oj,dj}\{ P^j_k, o_j, d_j \}{Pkj​,oj​,dj​}：

边缘感知渲染损失：3DGS中用于训练3D高斯的原始损失函数定义为：
$${\mathcal{L}}_I=(1-\lambda ){\mathcal{L}}_1+\lambda {\mathcal{L}}_{D-SSIM},$$
其中${\mathcal{L}}_1$和${\mathcal{L}}_{D-SSIM}$由真实图像监督。然而，由于边缘像素的稀疏分布，这种公式在边缘图优化中会出现梯度崩溃问题，常常导致所有高斯的透明度收敛到零。为了解决这个问题，作者提出了一种新颖的边缘感知损失函数${\mathcal{L}}_{\text{edge}}$，它取代了${\mathcal{L}}_1$，并平衡了边缘图中边缘和非边缘像素的影响。损失函数定义为：
$${\mathcal{L}}_{\text{edge}}=\frac{|{\mathcal{M}}_I|}{|{\mathcal{E}}_I|}\sum _{i\in {\mathcal{N}}_I}{\Vert I_i-{\hat{I}}_i\Vert }_2^2+\frac{|{\mathcal{N}}_I|}{|{\mathcal{E}}_I|}\sum _{i\in {\mathcal{M}}_I}{\Vert I_i-{\hat{I}}_i\Vert }_2^2,$$
其中：
- ${\mathcal{M}}_I$表示当前边缘图中边缘像素的集合（强度大于阈值$\eta =0.1$的像素），${\mathcal{N}}_I$表示非边缘像素的集合，${\mathcal{E}}_I$表示所有像素的集合。
- $I_i$和${\hat{I}}_i$分别是渲染的高斯图像和真实边缘图中的像素值。

该函数通过在优化过程中自适应平衡边缘和非边缘区域的贡献，增强了模型区分边缘像素的能力。

平滑连接正则化：为了确保学习到的曲线之间平滑连接，作者设计了一个正则化项，使相邻端点之间的距离最小化。设$P_i$和$P_j$分别表示第$i$条和第$j$条曲线的端点（起点或终点）。端点连接正则化项定义为：
$${\mathcal{L}}_{\text{conn}}=\sum _{i=1}^M\sum _{j=1}^M\mathbb{I}({\Vert P_i-P_j\Vert }_2<\tau )\cdot {\Vert P_i-P_j\Vert }_2^2,$$
其中$M$是曲线的总数，$\tau$是距离阈值，$\mathbb{I}(\cdot )$是指示函数，如果${\Vert P_i-P_j\Vert }_2<\tau$则等于1，否则为0。

平滑曲线正则化：为了确保更平滑的曲线轨迹，作者引入了一个额外的损失项作为曲线平滑度约束。通过最小化相邻采样点的高斯方向向量之间的差异来实现该约束。定义为：
$${\mathcal{L}}_{\text{smo}}=\sum _{j=1}^M\sum _{i=1}^{N_j-1}{\Vert {\mathbf{v}}_{j,i}^1-{\mathbf{v}}_{j,i+1}^1\Vert }_2^2,$$
其中$N_j$是第$j$条曲线上的采样点数量，${\mathbf{v}}_{j,i}^1$表示第$j$条曲线第$i$个采样点处的高斯方向向量。

简洁曲线正则化：为了促进简洁的曲线表示并增强优化收敛性，作者引入了一个额外的正则化项${\mathcal{L}}_{\text{reg}}$来约束曲线的不透明度：
$${\mathcal{L}}_{\text{reg}}=\sum _{j=1}^C\log \left(\frac{1+o_j^2}{0.5}\right),$$
其中$o_j$表示第$j$条曲线的不透明度。此外，为了消除冗余的高斯曲线，作者采用了一种受[11]启发的掩码损失${\mathcal{L}}_m$。

总之，训练参数曲线的最终损失函数定义如下：
$${\mathcal{L}}_{\text{all}}={\mathcal{L}}_{\text{edge}}+{\lambda }_1{\mathcal{L}}_{\text{conn}}+{\lambda }_2{\mathcal{L}}_{\text{smo}}+{\lambda }_3{\mathcal{L}}_{\text{reg}}+{\lambda }_4{\mathcal{L}}_m.$$
这里公式1中的${\mathcal{L}}_r$实现为${\mathcal{L}}_{\text{all}}$。

四、实验

4.1实验设置

数据集：作者在三个公共基准上评估该方法：ABC - NEF [35]、MV2Cyl的真实物体 [8] 和Replica [26]。与EMAP和EdgeGaussians [5]一致，作者使用ABC - NEF数据集的一个选定子集，该子集包含来自ABC数据集 [10] 的82个CAD模型。每个模型提供参数化的真实边缘用于定量3D边缘评估，以及50个渲染视图，这些视图捕捉了不同的物体视角。MV2Cyl [8] 引入了一组通过3D打印Fusion360 [30] 中各种草图拉伸模型创建的真实世界物体，提供多视图图像、相机姿态和CAD模型。作者展示6个物体来评估真实世界物体的性能。对于Replica，每个场景提供100个多视图边缘图用于全面评估。由于缺乏真实边缘注释，对Replica的分析主要集中在定性比较上，以评估该方法在复杂场景中的有效性。

基线：将该方法与四种用于3D直线和曲线重建的最先进基线进行比较，其中包括三种基于学习的方法，NEF [35]、EdgeGaussians [5] 和EMAP [12]，以及一种基于直线的运动恢复结构（SfM）方法LIMAP [15]。

指标：遵循 [5, 12] 中建立的指标，作者使用准确率（Acc.）、以毫米（mm）为单位测量的完整性（Comp.），以及以百分比表示的召回率（$R_{\tau }$）、精度（$P_{\tau }$）、F分数（$F_{\tau }$）来评估性能，距离阈值为$\tau$（单位为mm）。这些指标通过按参数化边缘长度的比例采样点并将其下采样到与真实边缘相同的分辨率来计算。此外，为了比较效率，作者提供训练时间，并且为了展示所提出的参数化曲线的紧凑性，作者报告生成的曲线/直线的数量。

实现细节：作者的方法对每个测试实例训练10000次迭代。为了确保有意义的更新，作者将参数化边缘的自适应控制策略延迟到训练的后期阶段引入，因为这些边缘需要充分优化才能收敛到合适的形式。具体来说，曲线线性化在第3000次迭代时启动。从第7000次迭代开始，作者应用曲线线性化和合并策略来细化参数曲线。为了平衡效率，拆分、线性化和合并操作每1000次迭代执行一次。此外，作者在第7000次迭代之前优化曲线不透明度。在此之后，不透明度属性固定，并应用掩码损失。

4.2评估

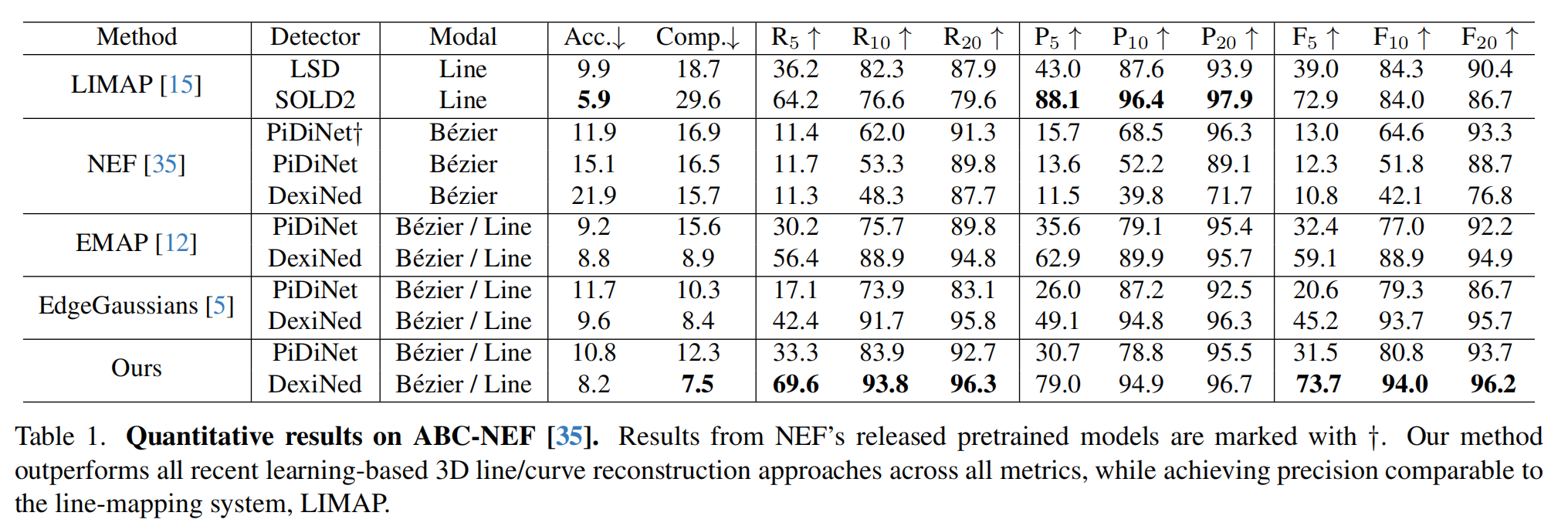
ABC - NEF数据集 [35] 上的评估：定性和定量比较分别如图4和表1所示。遵循EMAP，作者使用PiDiNet [27] 和DexiNed [22] 作为边缘检测器进行定量报告结果，而可视化结果展示了DexiNed的性能。LIMAP实现了令人印象深刻的精度，但缺乏表示曲线的能力，在对这种几何元素进行建模时经常导致显著的边缘遗漏。NEF由于点采样和基于拟合的后处理的限制而表现出较低的准确性。EMAP在重建不完整方面存在困难，导致完整性和召回率得分较低。EdgeGaussians经常产生碎片化或缺失的重建结果，主要是由于在估计构造高斯的主轴时不准确，这导致后续拟合过程收敛到次优局部最小值。作者的方法直接优化参数边缘表示，固有地纳入局部边缘约束并消除后处理拟合阶段引入的误差。结果，所提出的方法在所有指标上都优于所有基于学习的方法，同时实现了与LIMAP相当的精度。

为了进一步比较参数边缘提取的效率和紧凑性，作者还在ABC - NEF基准上进行评估，测量运行时间和参数边缘的数量。使用DexiNed作为默认的图像边缘检测器。EdgeGaussians和作者的方法在计算效率方面都显著优于基于隐式表示的方法，如NEF和EMAP。NEF由于频繁的边缘遗漏而使用最少的边缘，这反映在其较低的召回率得分中。作者的方法在实现完整且高度准确的边缘重建的同时，实现了紧凑的参数边缘表示和高效的重建。它在效率、紧凑性和重建质量之间显示出卓越的平衡。补充材料中提供了更多比较。

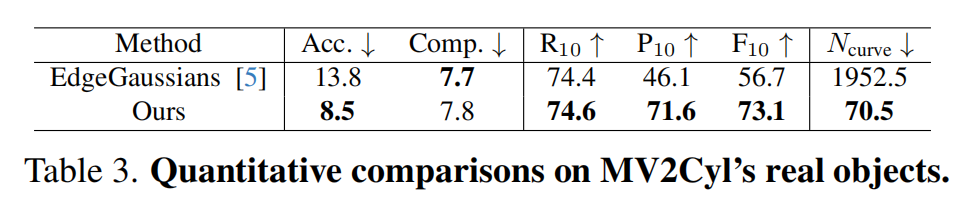
MV2Cyl真实物体 [8] 上的评估：由于不同视角导致的边缘检测不一致，以及确保物体在相机视野内均匀覆盖的困难，真实世界数据集通常对算法构成重大挑战。由于NEF和EMAP在作者的实验中未能产生合理的3D边缘，作者将自己的方法与EdgeGaussian进行比较。如图1所示，作者的方法展示了更好的逆向工程能力。由于真实世界场景中光照和视角变化引入的2D边缘噪声，EdgeGaussian生成了大量有噪声的高斯分布。相比之下，作者的方法固有地强制局部一致性约束并更好地减轻噪声的影响。对于定性评估，作者遵循MV2Cyl [8] 并使用ICP将重建的边缘点云与真实CAD模型对齐。表3显示作者的方法实现了更高的准确性和更紧凑的3D边缘。

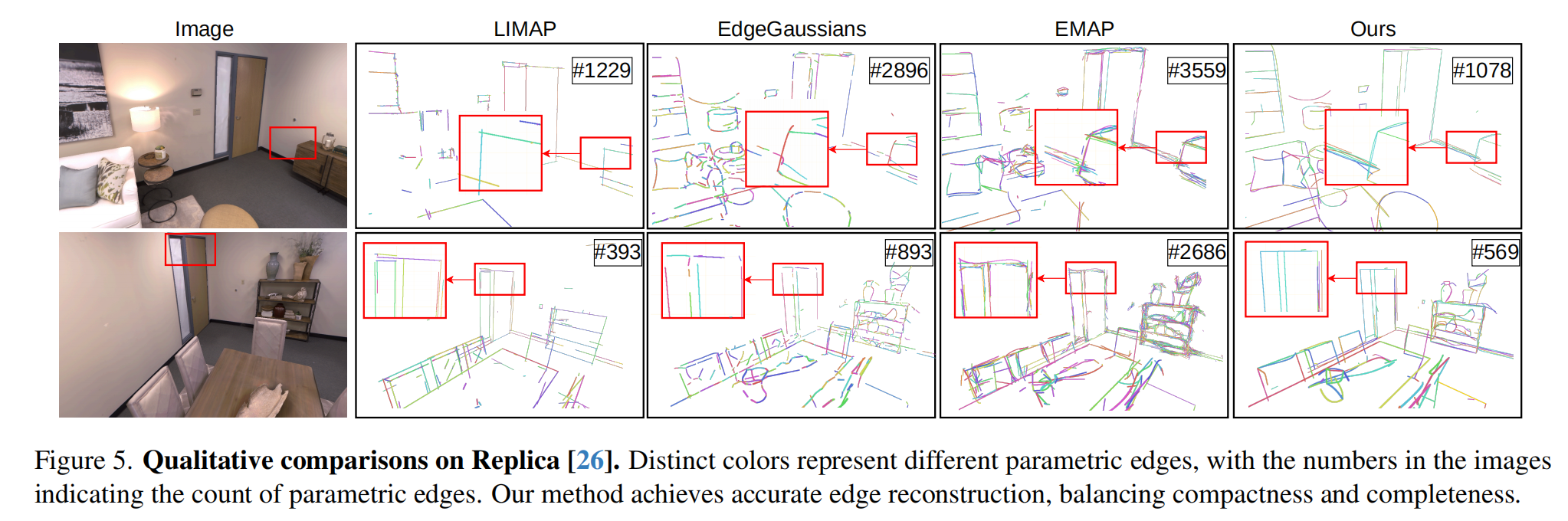
Replica数据集 [26] 上的评估：为了展示作者的方法在捕捉场景级几何方面的能力，作者在Replica数据集上进一步评估它。由于NEF难以有效处理大规模场景，作者将其重建结果排除在该实验之外。由于缺乏真实3D边缘，作者仅专注于定性比较以评估不同方法的性能。如图5所示，作者比较了不同方法的可视化边缘和重建边缘的数量。作者的方法即使在场景级别也保持其优越性，受益于参数曲线表示的直接优化。作者的方法产生的边缘数量与LIMAP相似，而LIMAP存在严重的边缘遗漏问题。与EdgeGaussians和EMAP相比，作者的方法在使用更少的参数边缘的同时实现了相当的重建准确性，确保了紧凑且高效的表示。这有利于下游应用，并能够对重建的边缘进行更可解释的理解。

4.3消融实验与分析

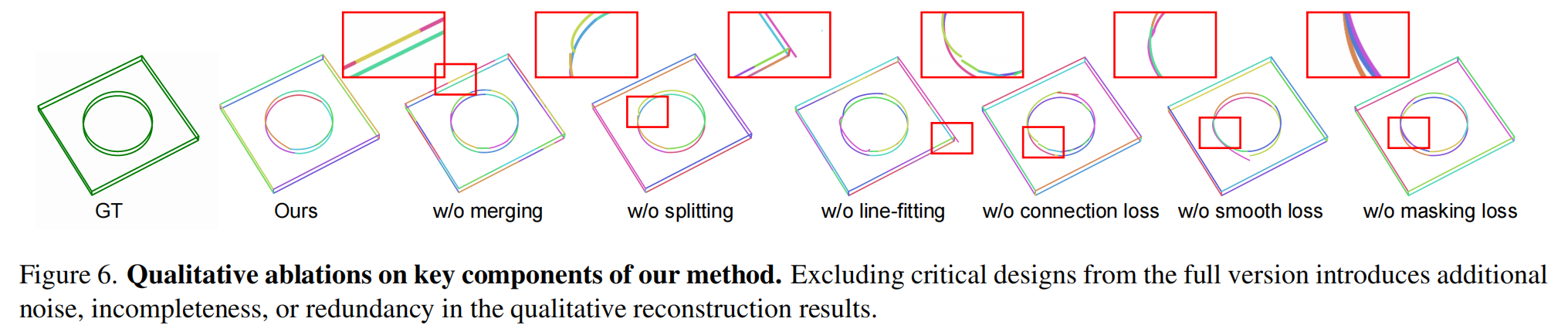
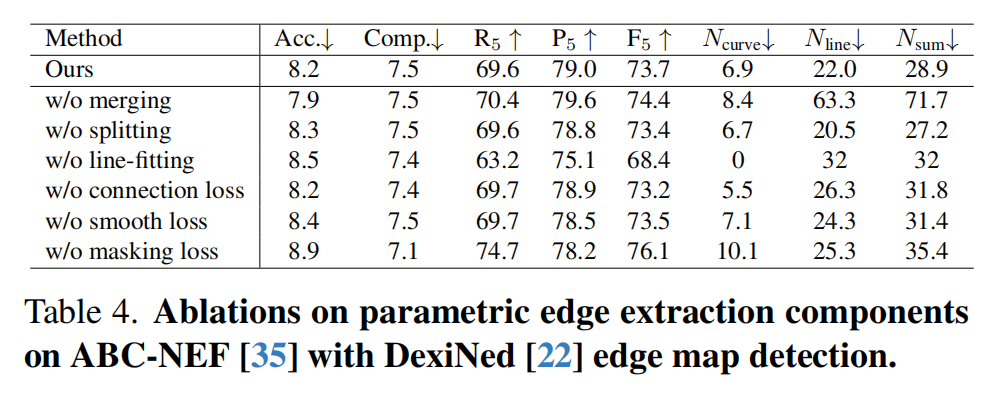
作者进行消融实验以验证关键损失函数和自适应参数曲线控制策略的有效性，如表4和图6所示。消融实验在ABC - NEF基准上进行，使用DexiNed作为边缘检测器。首先，去除曲线合并操作会导致召回率和精度略有增加，但会导致重建曲线的数量显著增加，这对于实现紧凑表示是不可取的。其次，禁用曲线拆分操作会引入噪声、锯齿状曲线，表明其对于噪声控制的必要性。第三，消除直线拟合操作会导致准确性和完整性明显下降，因为直线在人造物体中很常见，并且更容易合并，有助于整体简化。第四，去除鼓励曲线端点连接的损失函数会降低重建准确性，并导致参数曲线表示不那么紧凑。第五，平滑损失对于提高重建准确性和减少噪声至关重要。最后，掩码损失有效地消除了冗余曲线。没有这个损失，该方法倾向于产生重叠曲线并引入更多噪声边缘。整合所有组件后，作者的参数边缘提取管道在准确性、完整性和紧凑性之间实现了最佳平衡。

五、结论

本文提出了一种基于参数曲线与面向边缘的高斯之间双向耦合机制的单阶段3D参数曲线重建方法。其局限性在于该方法仍然依赖于2D边缘图的质量，这可以通过2D基础模型来估计更好的边缘图来缓解。作者的方法也为将2D边缘检测基础模型提升到3D提供了一条潜在途径和未来方向，以有利于3D视觉和几何推理。

声明

本文内容为论文学习收获分享，受限于知识能力，本文对原文的理解可能存在偏差，最终内容以原论文为准。本文信息旨在传播和学术交流，其内容由作者负责，不代表本号观点。文中作品文字、图片等如涉及内容、版权和其他问题，请及时与我们联系，我们将在第一时间回复并处理。