如果把深度学习比作一座高楼,那数学与机器学习基础就是支撑这座高楼的地基。无论是复杂的卷积神经网络(CNN)、循环神经网络(RNN),还是当下热门的Transformer模型,其底层逻辑都离不开线性代数的数据表示、概率论的不确定性建模,以及优化算法的参数学习。
一、数学基础:深度学习的“语言系统”
数学是描述深度学习模型的“通用语言”——线性代数帮我们处理高维数据结构,概率论帮我们应对现实世界的不确定性,优化算法则帮模型找到最优解。这三者相辅相成,缺一不可。
1. 线性代数:用“数组”描述世界
线性代数的核心是用结构化的数字(标量、向量、矩阵、张量)表示数据,并通过运算提取数据规律。
(1)四大数学对象:从“单个数字”到“高维结构”
我们先明确最基本的“数据单元”,它们的区别本质是维度不同:
- 标量(Scalar):单个数字,比如“身高180cm”“体重70kg”,用不加粗的小写字母表示(如a,b,xa, b, xa,b,x)。
- 向量(Vector):一维数组,对应“一个样本的多个特征”,比如用向量x=[180,70,25]x = [180, 70, 25]x=[180,70,25]表示“身高180cm、体重70kg、年龄25岁”的人,用加粗小写字母表示(如a,b,x\mathbf{a}, \mathbf{b}, \mathbf{x}a,b,x)。
- 矩阵(Matrix):二维数组,对应“多个样本的特征集合”,比如100个人的身高、体重、年龄数据,就是一个100×3100 \times 3100×3的矩阵,用加粗大写字母表示(如A,B,X\mathbf{A}, \mathbf{B}, \mathbf{X}A,B,X)。
- 张量(Tensor):n维数组(n≥3n \geq 3n≥3),对应“更复杂的结构化数据”,比如一张RGB图像是width×height×3width \times height \times 3width×height×3的3维张量(3个通道:红、绿、蓝),一段视频则是time×width×height×3time \times width \times height \times 3time×width×height×3的4维张量,用带箭头的加粗大写字母表示(如A⃗,B⃗\vec{\mathbf{A}}, \vec{\mathbf{B}}A,B)。
举个直观例子:
- 标量:一杯水的温度(25℃);
- 向量:一杯水的“温度、体积、pH值”([25, 500, 7]);
- 矩阵:10杯不同水的“温度、体积、pH值”(10行3列);
- 张量:10杯水分别在“早上、中午、晚上”的3个特征(10行3列3层,3维张量)。
(2)核心运算:从“数据操作”到“规律提取”
线性代数的运算本质是“对结构化数据做变换”,重点掌握3种核心运算:
| 运算类型 | 定义与规则 | 应用场景举例 |
|---|---|---|
| 矩阵转置(A⊤A^\topA⊤) | 行变列、列变行(如m×nm \times nm×n矩阵转置后为n×mn \times mn×m) | 样本特征与权重的维度匹配 |
| 矩阵乘法(C=ABC=ABC=AB) | 要求A的列数=B的行数,结果Ci,j=∑kAi,kBk,jC_{i,j} = \sum_k A_{i,k}B_{k,j}Ci,j=∑kAi,kBk,j(行乘列求和) | 特征与权重的线性组合(如y^=w⊤x\hat{y} = \mathbf{w}^\top \mathbf{x}y^=w⊤x) |
| 元素积(阿达玛乘积)(C=A⊙BC=A\odot BC=A⊙B) | 对应元素相乘,要求A和B维度完全相同,Ci,j=Ai,jBi,jC_{i,j}=A_{i,j}B_{i,j}Ci,j=Ai,jBi,j | 元素级的特征缩放(如激活函数前的逐元素乘法) |
关键性质提醒:
- 分配律:A(B + C) = AB + AC
- 结合律:A(BC) = (AB)C
- 矩阵乘法不满足交换律(AB≠BAAB \neq BAAB=BA),比如A是2×32 \times 32×3矩阵,B是3×23 \times 23×2矩阵,AB是2×22 \times 22×2,BA是3×33 \times 33×3,维度都不同;
- 但向量内积满足交换律(x⊤y=y⊤x\mathbf{x}^\top \mathbf{y} = \mathbf{y}^\top \mathbf{x}x⊤y=y⊤x),因为结果是标量;
- 转置的“逆运算”:(AB)⊤=B⊤A⊤(AB)^\top = B^\top A^\top(AB)⊤=B⊤A⊤(先乘后转置 = 先转置后反向乘),这是神经网络反向传播的重要公式。
- 对n维向量x:Ix = x
- 对n×m矩阵A:IA = A
- 只有方阵(n×n)且满足可逆条件时,才存在逆矩阵A⁻¹。其关键特性是:A⁻¹与A相乘的结果为单位矩阵I,即A⁻¹A = I。
- 逆矩阵主要用于求解线性方程组:例如已知Ax = b(求解向量x),只需在等式两边左乘A⁻¹,即可得到x = A⁻¹b。这类似于数字运算中"a x = b → x = b/a(a≠0)"的过程。在矩阵运算中,“除以矩阵A"等价于"乘以A的逆矩阵”。
单位矩阵是方阵(行数=列数,记为I∈Rn×n{I} \in \mathbb{R}^{n \times n}I∈Rn×n),它的形式很规律:主对角线(左上到右下)的元素全为1,其余位置全为0,比如: I=(10…001…0⋮⋮⋱⋮00…1) {I} = \begin{pmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \end{pmatrix} I= 10⋮001⋮0……⋱…00⋮1
(3)线性方程组与范数:解决“数据拟合”与“大小衡量”
{A1,1x1+A1,2x2+⋯+A1,nxn=b1A2,1x1+A2,2x2+⋯+A2,nxn=b2 ⋮Am,1x1+Am,2x2+⋯+Am,nxn=bm \begin{cases} A_{1,1}x_1 + A_{1,2}x_2 + \dots + A_{1,n}x_n = b_1 \\ A_{2,1}x_1 + A_{2,2}x_2 + \dots + A_{2,n}x_n = b_2 \\ \ \ \vdots \\ A_{m,1}x_1 + A_{m,2}x_2 + \dots + A_{m,n}x_n = b_m \\ \end{cases} ⎩ ⎨ ⎧A1,1x1+A1,2x2+⋯+A1,nxn=b1A2,1x1+A2,2x2+⋯+A2,nxn=b2 ⋮Am,1x1+Am,2x2+⋯+Am,nxn=bm
- 线性方程组 Ax=bAx = bAx=b:深度学习中“线性拟合”的本质。比如用x\mathbf{x}x(特征)预测b\mathbf{b}b(标签),A\mathbf{A}A是特征矩阵,x\mathbf{x}x是待求的权重。根据维度关系,解的情况分为3类:
- 欠定(m<nm < nm<n):方程数少于未知数,无数解(如“x1+x2=5x_1 + x_2 = 5x1+x2=5”,两个变量一个方程);
- 适定(m=nm = nm=n且A\mathbf{A}A可逆):方程数等于未知数,唯一解(x=A−1bx = A^{-1}bx=A−1b);
- 超定(m>nm > nm>n):方程数多于未知数,可能无解(如“x1+x2=5x_1 + x_2 = 5x1+x2=5且x1+x2=6x_1 + x_2 = 6x1+x2=6”)。
范数(Norm):衡量“向量/矩阵的大小”,是正则化、损失函数的核心。范数本质上是一类“函数”,它为向量(或矩阵)定义了一个非负的“长度”或“大小”。
范数是一种衡量“向量/矩阵大小”的函数fff,需满足4个规则:
- 非负性:对任意输入,结果都非负(f(x)≥0f({x}) \geq 0f(x)≥0);
- 零向量专属:只有输入是零向量时,结果才为0(f(x)=0 ⟹ x=0f({x}) = 0 \implies {x} = 0f(x)=0⟹x=0);
- 三角不等式:两个向量相加后的范数,不超过各自范数的和(f(x+y)≤f(x)+f(y)f({x} + {y}) \leq f({x}) + f({y})f(x+y)≤f(x)+f(y));
- 齐次性:向量乘以数α\alphaα,范数等于α\alphaα的绝对值乘以原向量范数(f(αx)=∣α∣f(x)f(\alpha {x}) = |\alpha| f({x})f(αx)=∣α∣f(x))。
向量的LpL_pLp范数是“范数”中最具代表性的一类,其核心定义为:
对于nnn维向量x=(x1,x2,…,xn)⊤{x} = (x_1, x_2, \dots, x_n)^\topx=(x1,x2,…,xn)⊤,LpL_pLp范数的数学表达式为:
∥x∥p=(∑i=1n∣xi∣p)1p \|{x}\|_p = \left( \sum_{i=1}^n |x_i|^p \right)^{\frac{1}{p}} ∥x∥p=(i=1∑n∣xi∣p)p1
其中p∈Rp \in \mathbb{R}p∈R且p>1p > 1p>1。
当ppp取不同的特殊值时,LpL_pLp范数会退化为我们更熟悉的形式。下面重点介绍最常用的三种:L1L_1L1范数、L2L_2L2范数和L∞L_\inftyL∞范数。
1. L1L_1L1范数:“曼哈顿距离”的数学缩影
当p=1p = 1p=1时,代入LpL_pLp范数的定义式,可得到: ∥x∥1=∑i=1n∣xi∣ \|{x}\|_1 = \sum_{i=1}^n |x_i| ∥x∥1=i=1∑n∣xi∣
直观来说,L1L_1L1范数是向量各分量绝对值的和。比如,对向量x=(3,−2,5)⊤{x} = (3, -2, 5)^\topx=(3,−2,5)⊤,其L1L_1L1范数为: ∥x∥1=∣3∣+∣−2∣+∣5∣=3+2+5=10 \|{x}\|_1 = |3| + |-2| + |5| = 3 + 2 + 5 = 10 ∥x∥1=∣3∣+∣−2∣+∣5∣=3+2+5=10
应用场景: L1L_1L1范数最经典的应用是Lasso回归(带L1L_1L1正则化的线性回归)。由于L1L_1L1范数天然具有“让向量分量稀疏”的特性(倾向于让很多分量变为0),Lasso能在训练模型时自动筛选特征——把不重要的特征系数压缩到0,只保留关键特征。
此外,在压缩感知(从少量观测恢复高维信号)、稀疏编码(用少量“基向量”表示信号)等领域,L1L_1L1范数也被用来利用“信号的稀疏性”,实现高效的数据压缩或噪声去除。
2. L2L_2L2范数:欧几里得空间的“天然长度”
当p=2p = 2p=2时,L2L_2L2范数有一个更家喻户晓的名字——欧几里得范数(Euclidean Norm)。此时定义式可简化为: ∥x∥2=x⊤x \|{x}\|_2 = \sqrt{{x}^\top {x}} ∥x∥2=x⊤x
展开后更直观:x⊤x=x12+x22+⋯+xn2{x}^\top {x} = x_1^2 + x_2^2 + \dots + x_n^2x⊤x=x12+x22+⋯+xn2,因此:
∥x∥2=x12+x22+⋯+xn2 \|{x}\|_2 = \sqrt{x_1^2 + x_2^2 + \dots + x_n^2} ∥x∥2=x12+x22+⋯+xn2这正是我们在初中几何里就学过的“欧几里得距离”——向量到原点的“直线距离”。比如二维向量x=(3,4)⊤{x} = (3, 4)^\topx=(3,4)⊤,其L2L_2L2范数为32+42=5\sqrt{3^2 + 4^2} = 532+42=5,完美契合勾股定理。
应用场景: L2L_2L2范数是最常用的“距离度量”,比如机器学习中KNN(K近邻)算法,就常用欧几里得距离判断样本间的相似度。
在模型训练中,Ridge回归(带L2L_2L2正则化的线性回归)用L2L_2L2范数限制参数的“大小”,防止模型因参数过大而“过拟合”(让模型更“平滑”,泛化能力更强)。
L2 约束 x² + y² <= k 是一个圆形。目标函数的等高线(一个椭圆)与这个圆相切时,切点(最优解)几乎永远不会在轴上。
L1 约束 |x| + |y| <= k 是一个菱形。目标函数的等高线与这个菱形相切时,切点(最优解)有非常高的概率落在菱形的尖角上,也就是 X轴 或 Y轴上,从而导致 x=0 或 y=0。
为什么稀疏解有用?
在机器学习中,这个特性极其宝贵:特征选择(Feature Selection):假设你的特征向量 [x1, x2, x3, …, x100]
代表100个不同的因素(如年龄、收入、地点…)来预测房价。使用L1正则化后,训练出的模型权重向量 [w1, w2, w3, …,
w100] 可能会有很多 0。这意味着那些权重为 0
的特征被模型认为是无关紧要的,可以被安全地忽略。L1正则化自动帮你进行了特征选择,得到了一个更简单、可解释性更强的模型。
模型压缩:稀疏模型占用的存储空间和计算资源更少,因为可以跳过所有0的计算。
矩阵的Frobenius范数
它是矩阵的一种常用范数,计算方法是:把矩阵所有元素的平方相加,再开平方根,公式为:
∥A∥F=∑i,jAi,j2\|{A}\|_F = \sqrt{\sum_{i,j} A_{i,j}^2}∥A∥F=i,j∑Ai,j2
比如矩阵A=(1234){A} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}A=(1324),其Frobenius范数为12+22+32+42=30\sqrt{1^2 + 2^2 + 3^2 + 4^2} = \sqrt{30}12+22+32+42=30。
3. L∞L_\inftyL∞范数:“最大分量”的直接度量
当p→∞p \to \inftyp→∞时,LpL_pLp范数的极限形式就是L∞L_\inftyL∞范数,其定义为: ∥x∥∞=maxi∣xi∣ \|{x}\|_\infty = \max_{i} |x_i| ∥x∥∞=imax∣xi∣
简单来说,L∞L_\inftyL∞范数是向量各分量绝对值的最大值。比如向量x=(3,−5,2)⊤{x} = (3, -5, 2)^\topx=(3,−5,2)⊤,其L∞L_\inftyL∞范数为max{∣3∣,∣−5∣,∣2∣}=5\max\{|3|, |-5|, |2|\} = 5max{∣3∣,∣−5∣,∣2∣}=5。
应用场景: L∞L_\inftyL∞范数常用于鲁棒性要求高的领域:比如控制系统中,衡量系统对“最大扰动”的容忍度;在图像处理中,可用于衡量“图像块之间的最大差异”,辅助图像分割、图像匹配等任务。
2. 概率论:用“概率”应对不确定性
现实世界的数据充满随机性(比如“明天是否下雨”“用户是否点击广告”),概率论帮我们量化不确定性,并从随机数据中提取规律。
(1)随机变量与概率分布:描述“随机事件的可能性”
- 随机变量:取值不确定的变量,分离散(如“抛硬币结果:0或1”)和连续(如“人的身高:150~200cm”)。
- 概率分布:随机变量取每个值的可能性,核心是“如何计算概率”:
- 离散变量用概率质量函数(PMF):比如伯努利分布(二元结果,如“点击=1,不点击=0”),满足0≤P(x)≤10 \leq P(x) \leq 10≤P(x)≤1且∑xP(x)=1\sum_x P(x) = 1∑xP(x)=1;
- 离散变量的概率分布可以用**概率质量函数 (PMF)**来表示
- x=xx = xx=x 的概率表示为 P(x)P(x)P(x) 或 P(x=x)P(x = x)P(x=x)
- x∼P(x)x \sim P(x)x∼P(x) 指定了 xxx 服从的分布
- 联合概率分布
- P(x=x,y=y)P(x = x, y = y)P(x=x,y=y) 或 P(x,y)P(x, y)P(x,y) 表示 x=xx = xx=x 和 y=yy = yy=y 同时出现的概率
- 连续变量用概率密度函数(PDF):比如高斯分布(正态分布,如“身高分布”),满足p(x)≥0p(x) \geq 0p(x)≥0且∫p(x)dx=1\int p(x)dx = 1∫p(x)dx=1(注意:PDF本身不是概率,概率是区间积分,比如“身高170~180cm的概率”是∫170180p(x)dx\int_{170}^{180} p(x)dx∫170180p(x)dx)。
(2)三大核心概念:边缘、条件、独立
这三个概念是“从数据中挖掘关联”的关键:
联合概率(Joint Probability)可以理解为:多个随机变量 “同时发生某件事” 的概率。
边缘概率分布:在多变量的联合概率分布里,只关注其中一部分变量的概率分布。
离散随机变量的情况
比如有两个离散随机变量x 和y,它们的联合概率分布是P(x,y)表示“ x 取某值且y 取某值”的概率。若想得到x 单独的概率分布(即x 的边缘概率分布),需要把所有可能的y 对应的联合概率“加起来”,公式为:P(x=x)=∑yP(x=x,y=y) P(x = x) = \sum_{y} P(x = x, y = y) P(x=x)=y∑P(x=x,y=y)连续随机变量的情况
如果是两个连续随机变量x 和y,它们的联合概率密度函数(PDF)是p(x,y)。若想得到x 单独的概率密度(即x 的边缘概率密度**),需要把y 的所有可能值“积分掉”(积分是连续版本的“求和”),公式为:p(x)=∫p(x,y)dy p(x) = \int p(x,y) dy p(x)=∫p(x,y)dy条件概率:在某个事件已经发生的前提下,另一个事件发生的概率,公式为
P(y∣x)=P(x,y)P(x)(P(x)≠0)P(y|x) = \frac{P(x,y)}{P(x)}(P(x) \neq 0)P(y∣x)=P(x)P(x,y)(P(x)=0)
P(y=y∣x=x)=P(y=y,x=x)P(x=x)(P(x)≠0) P(y = y | x = x) = \frac{P(y = y, x = x)}{P(x = x)} (P(x) \neq 0)P(y=y∣x=x)=P(x=x)P(y=y,x=x)(P(x)=0)链式法则:把多事件概率“化繁为简”
当要处理多个事件(比如n 个事件x(1),x(2),…,x(n){x^{(1)}, x^{(2)}, \dots, x^{(n)} }x(1),x(2),…,x(n)同时发生的概率时,“链式法则”能帮我们把复杂的“联合概率”拆成简单的“条件概率乘积”。
P(x(1),…,x(n))=P(x(1))∏i=2nP(x(i)∣x(1),…,x(i−1)) P(x^{(1)}, \dots, x^{(n)}) = P(x^{(1)}) \prod_{i=2}^{n} P(x^{(i)} | x^{(1)}, \dots, x^{(i-1)}) P(x(1),…,x(n))=P(x(1))i=2∏nP(x(i)∣x(1),…,x(i−1))
P(x(1),x(2),x(3))=P(x(1))⋅P(x(2)∣x(1))⋅P(x(3)∣x(1),x(2)) P(x^{(1)}, x^{(2)}, x^{(3)}) = P(x^{(1)}) \cdot P(x^{(2)} | x^{(1)}) \cdot P(x^{(3)} | x^{(1)}, x^{(2)}) P(x(1),x(2),x(3))=P(x(1))⋅P(x(2)∣x(1))⋅P(x(3)∣x(1),x(2))
通俗理解就是:- 先计算“第一个事件x(1)x^{(1)}x(1)发生的概率”;
- 再依次计算“在前面所有事件x(1)x^{(1)}x(1) 到 x(i−1)x^{(i-1)}x(i−1)都发生的前提下,第i 个事件 x(i)x^{(i)}x(i)发生的概率”;
- 最后把这些概率相乘,就得到所有事件同时发生的联合概率。
独立性:若两个随机变量x 和y 满足“联合概率能拆成各自概率的乘积”,则称它们相互独立,记作 x⊥yx \perp yx⊥y。用公式严格定义为:
∀x∈X,y∈Y,p(x=x,y=y)=p(x=x)⋅p(y=y) \forall x \in \mathcal{X}, y \in \mathcal{Y}, \quad p(x = x, y = y) = p(x = x) \cdot p(y = y)∀x∈X,y∈Y,p(x=x,y=y)=p(x=x)⋅p(y=y)
独立性的本质是“一个变量的发生,不会改变另一个变量发生的概率”。条件独立性:“第三方”介导下的独立
现实中,变量关系往往更复杂:两个变量本身不独立,但给定“第三方变量z”后,它们会变得独立——这就是条件独立性,记作 x⊥y ∣ zx \perp y \ | \ zx⊥y ∣ z。公式定义为:
∀x∈X,y∈Y,z∈Z,p(x=x,y=y ∣ z=z)=p(x=x ∣ z=z)⋅p(y=y ∣ z=z) \forall x \in \mathcal{X}, y \in \mathcal{Y}, z \in \mathcal{Z}, \quad p(x = x, y = y \ | \ z = z) = p(x = x \ | \ z = z) \cdot p(y = y \ | \ z = z) ∀x∈X,y∈Y,z∈Z,p(x=x,y=y ∣ z=z)=p(x=x ∣ z=z)⋅p(y=y ∣ z=z)
“条件”的作用是“屏蔽”或“解释”了两个变量的依赖关系——当我们知道“第三方z”的信息后,( x 和y 就不再相互影响。
例如:
变量x:洒水车是否工作(工作/不工作);
变量y:地面是否潮湿(潮湿/干燥);
变量z:天气是否下雨(下雨/晴天)。
若不知道天气(z 未知):“洒水车工作”(x)和“地面潮湿”(y)有关联——洒水车工作可能导致地面潮湿。
若给定天气z 后,“洒水车是否工作”与“地面是否潮湿”变得相互独立——这就是条件独立性。
条件独立性在概率图模型(如贝叶斯网络、马尔可夫随机场)中至关重要。复杂的高维联合概率,可通过“条件独立”假设分解为低维条件概率的乘积,大幅简化计算与模型结构。
(3)期望:量化“数据的统计特征”
1. 期望的核心定义
函数 f(x)f(x)f(x) 的期望,描述的是:当 xxx 按照概率分布 P(x)P(x)P(x) 随机取值(“采样”)时,函数 f(x)f(x)f(x) 的平均值。
简单说,期望就是“用概率当权重,对函数值做加权平均”——概率大的 xxx 对应的 f(x)f(x)f(x),对平均值的“贡献”更大。
2. 离散变量的期望(求和版)
如果 xxx 是离散变量(比如 xxx 只能取“1,2,3”或“红、黄、蓝”等有限/可列个值),概率分布 P(x)P(x)P(x) 是“每个 xxx 出现的概率”(比如 P(1)=0.3P(1)=0.3P(1)=0.3 表示 x=1x=1x=1 的概率是 0.3)。
此时,期望的计算是对所有可能的 xxx,把“概率 P(x)P(x)P(x) 乘以对应的 f(x)f(x)f(x)”再求和,公式为:
Ex∼P[f(x)]=∑xP(x)f(x) \mathbb{E}_{x \sim P}\left[ f(x) \right] = \sum_{x} P(x) f(x) Ex∼P[f(x)]=x∑P(x)f(x)
- 例子:假设 xxx 只能取 1 和 2,且 P(1)=0.5P(1)=0.5P(1)=0.5,P(2)=0.5P(2)=0.5P(2)=0.5;函数 f(x)=2xf(x) = 2xf(x)=2x。
则期望为:
Ex∼P[f(x)]=P(1)f(1)+P(2)f(2)=0.5×2×1+0.5×2×2=1+2=3 \mathbb{E}_{x \sim P}\left[ f(x) \right] = P(1)f(1) + P(2)f(2) = 0.5 \times 2 \times 1 + 0.5 \times 2 \times 2 = 1 + 2 = 3 Ex∼P[f(x)]=P(1)f(1)+P(2)f(2)=0.5×2×1+0.5×2×2=1+2=3
这就是 f(x)f(x)f(x) 在 xxx 以 50% 概率取 1、50% 概率取 2 时的“加权平均值”。
3. 连续变量的期望(积分版)
如果 xxx 是连续变量(比如 xxx 可以取“0 到 1 之间的任意实数”),概率分布用概率密度函数 p(x)p(x)p(x) 描述(密度函数需通过“积分”计算概率,比如 xxx 在 ([a,b]) 内的概率是 ∫abp(x)dx\int_{a}^{b} p(x)dx∫abp(x)dx)。
此时,期望的计算是对 xxx 的所有可能取值范围,把“密度 p(x)p(x)p(x) 乘以对应的 f(x)f(x)f(x)”再积分,公式为:
Ex∼P[f(x)]=∫p(x)f(x)dx \mathbb{E}_{x \sim P}\left[ f(x) \right] = \int p(x) f(x) dx Ex∼P[f(x)]=∫p(x)f(x)dx
- 例子:假设 xxx 服从“([0,1]) 上的均匀分布”(此时密度 p(x)=1p(x)=1p(x)=1,因为均匀分布的密度是 1区间长度\frac{1}{\text{区间长度}}区间长度1),函数 f(x)=xf(x) = xf(x)=x。
则期望为:
Ex∼P[f(x)]=∫011×x dx=x22∣01=12−0=0.5 \mathbb{E}_{x \sim P}\left[ f(x) \right] = \int_{0}^{1} 1 \times x \, dx = \left. \frac{x^2}{2} \right|_{0}^{1} = \frac{1}{2} - 0 = 0.5 Ex∼P[f(x)]=∫011×xdx=2x2 01=21−0=0.5
这就是 f(x)=xf(x)=xf(x)=x 在 xxx 均匀取 ([0,1]) 内所有值时的“加权平均值”(积分是“无限个小部分求和”的扩展)。
4. 符号简化与线性性质
符号简化:如果已经明确概率分布是 PPP,可以省略“∼P\sim P∼P”,直接写 Ex[f(x)]\mathbb{E}_{x}\left[ f(x) \right]Ex[f(x)],意思不变。
线性性质:期望满足“线性运算”的规则——如果 α\alphaα、β\betaβ 是与 xxx 无关的常数,那么:
Ex[αf(x)+βg(x)]=αEx[f(x)]+βEx[g(x)] \mathbb{E}_{x}\left[ \alpha f(x) + \beta g(x) \right] = \alpha \mathbb{E}_{x}\left[ f(x) \right] + \beta \mathbb{E}_{x}\left[ g(x) \right] Ex[αf(x)+βg(x)]=αEx[f(x)]+βEx[g(x)]
这说明:“对线性组合的期望”等于“期望的线性组合”。比如:E[2f(x)+3g(x)]=2E[f(x)]+3E[g(x)]\mathbb{E}\left[ 2f(x) + 3g(x) \right] = 2\mathbb{E}\left[ f(x) \right] + 3\mathbb{E}\left[ g(x) \right]E[2f(x)+3g(x)]=2E[f(x)]+3E[g(x)],无论 f,gf,gf,g 是什么函数,也无论 xxx 是离散还是连续,这个性质都成立。
函数f(x)f(x)f(x)的加权平均,是“数据的中心趋势”。离散情况E[f(x)]=∑xP(x)f(x)\mathbb{E}[f(x)] = \sum_x P(x)f(x)E[f(x)]=∑xP(x)f(x),连续情况E[f(x)]=∫p(x)f(x)dx\mathbb{E}[f(x)] = \int p(x)f(x)dxE[f(x)]=∫p(x)f(x)dx。比如“抛硬币正面得1分、反面得0分,期望是0.5分”;
- 方差(Var(f(x))Var(f(x))Var(f(x))):衡量“数据的波动程度”,公式为Var(f(x))=E[(f(x)−E[f(x)])2]Var(f(x)) = \mathbb{E}[(f(x) - \mathbb{E}[f(x)])^2]Var(f(x))=E[(f(x)−E[f(x)])2]。方差越大,数据越分散(如“股票价格方差大,风险高”);
- 协方差(Cov(f(x),g(y))Cov(f(x),g(y))Cov(f(x),g(y))):衡量“两个变量的线性关联”,正协方差表示“同增同减”,负协方差表示“一增一减”,0表示“线性无关”。协方差矩阵则是“多个变量间两两协方差的集合”,比如3个特征的协方差矩阵是3×33 \times 33×3,对角线是各特征的方差。
(4)方差:量化“数据的统计特征”
函数 f(x)f(x)f(x) 的方差,用来衡量当 xxx 按概率分布取值时,f(x)f(x)f(x) 的值波动有多大。
计算逻辑:先算 f(x)f(x)f(x) 与自身“期望”E[f(x)]\mathbb{E}[f(x)]E[f(x)] 的差距(即“偏离期望的程度”),再把差距“平方”(消除正负),最后对平方结果求期望。公式:
Var(f(x))=E[(f(x)−E[f(x)])2] \text{Var}(f(x)) = \mathbb{E}\left[(f(x) - \mathbb{E}[f(x)])^2\right] Var(f(x))=E[(f(x)−E[f(x)])2]
举例:若 f(x)f(x)f(x) 总是接近期望,方差小;若 f(x)f(x)f(x) 忽大忽小,方差大。
(5)协方差:量化“数据的统计特征”
两个函数 f(x)f(x)f(x) 和 g(y)g(y)g(y) 的协方差,衡量这两个函数的取值之间有没有线性关联,以及关联的强弱和变化幅度。
计算逻辑:分别算 f(x)f(x)f(x) 偏离自身期望的部分、g(y)g(y)g(y) 偏离自身期望的部分,再把这两部分相乘,最后对乘积求期望。公式:
Cov(f(x),g(y))=E[(f(x)−E[f(x)])(g(y)−E[g(y)])] \text{Cov}(f(x), g(y)) = \mathbb{E}\left[(f(x) - \mathbb{E}[f(x)])(g(y) - \mathbb{E}[g(y)])\right] Cov(f(x),g(y))=E[(f(x)−E[f(x)])(g(y)−E[g(y)])]
- 协方差为正:f(x)f(x)f(x) 大时,g(y)g(y)g(y) 也容易大;
- 协方差为负:f(x)f(x)f(x) 大时,g(y)g(y)g(y) 容易小;
- 协方差绝对值大:两者取值都爱“远离各自期望”,且变化幅度都大。
若研究的是 nnn 维随机向量 x{x}x(比如 x=(x1,x2,…,xn){x} = (x_1, x_2, \dots, x_n)x=(x1,x2,…,xn),每个 xix_ixi 都是随机变量),协方差矩阵是一个 n×nn \times nn×n 的表格,用来整体描述“x{x}x 各分量之间的协方差关系”。
矩阵中第 iii 行、第 jjj 列的元素,就是 xix_ixi 和 xjx_jxj 的协方差,即:
Cov(x)i,j=Cov(xi,xj) \text{Cov}({x})_{i,j} = \text{Cov}(x_i, x_j) Cov(x)i,j=Cov(xi,xj)
“fff 和 ggg 可以是 identity functions(恒等函数)”:若让 f(x)=xf(x)=xf(x)=x、g(y)=yg(y)=yg(y)=y(输入啥就输出啥的“恒等函数”),方差和协方差就能直接描述“变量 xxx 自身的波动”“变量 xxx 与 yyy 的关联”,这是最常用的场景(比如直接分析随机变量 xxx 的方差,或 xxx 与 yyy 的协方差)。
(6)常见的概率分布
1. 伯努利分布(二元离散分布)
核心内容:描述只有两种结果(0或1)的随机变量。
- 概率:P(x=1)=ϕP(x=1)=\phiP(x=1)=ϕ,P(x=0)=1−ϕP(x=0)=1-\phiP(x=0)=1−ϕ(可合并为 P(x=x)=ϕx(1−ϕ)1−xP(x=x)=\phi^x (1-\phi)^{1-x}P(x=x)=ϕx(1−ϕ)1−x);
- 期望与方差:E[x]=ϕ\mathbb{E}[x]=\phiE[x]=ϕ,Var(x)=ϕ(1−ϕ)\text{Var}(x)=\phi(1-\phi)Var(x)=ϕ(1−ϕ)。
举例:抛一枚均匀硬币,定义“正面朝上”为x=1x=1x=1,“反面朝上”为x=0x=0x=0,此时ϕ=0.5\phi=0.5ϕ=0.5,硬币结果服从伯努利分布。
2. 范畴分布(多分类离散分布)
核心内容:描述有kkk个互斥状态(kkk有限)的离散随机变量。
- 概率:P(x=i∣p)=piP(x=i|{p})=p_iP(x=i∣p)=pi,其中p∈[0,1]k{p} \in [0,1]^kp∈[0,1]k且∑i=1kpi=1\sum_{i=1}^k p_i = 1∑i=1kpi=1(pip_ipi是第iii个状态的概率)。
举例:掷一颗均匀骰子,结果有6种(k=6k=6k=6),每个面朝上的概率pi=16p_i = \frac{1}{6}pi=61,总和为1,骰子结果服从范畴分布。
3. 高斯分布(正态分布,连续单变量分布)
核心内容:描述连续型随机变量,呈“钟形”对称分布。
- 概率密度函数:N(x;μ,σ2)=12πσ2exp(−(x−μ)22σ2)\mathcal{N}(x;\mu,\sigma^2) = \sqrt{\frac{1}{2\pi\sigma^2}} \exp\left( -\frac{(x-\mu)^2}{2\sigma^2} \right)N(x;μ,σ2)=2πσ21exp(−2σ2(x−μ)2);
- 均值与方差:E[x]=μ\mathbb{E}[x]=\muE[x]=μ(分布峰值位置),Var[x]=σ2\text{Var}[x]=\sigma^2Var[x]=σ2(分布“胖瘦”,σ\sigmaσ为标准差);
- 中心极限定理:大量独立随机变量的和,近似服从正态分布。
举例:成年人的身高分布,大部分人身高集中在“平均身高”(如我国成年男性平均身高μ≈175cm\mu \approx 175\text{cm}μ≈175cm)附近,特别高或特别矮的人很少,符合高斯分布;又如班级数学考试成绩,中间分数段人数多、两端少,也近似正态分布。
4. 多元正态分布(连续多变量分布)
核心内容:描述多个连续随机变量的联合分布(即“随机向量”的分布)。
- 概率密度函数:N(x;μ,Σ)=1(2π)ddet(Σ)exp(−12(x−μ)⊤Σ−1(x−μ))\mathcal{N}({x};{\mu},{\Sigma}) = \sqrt{\frac{1}{(2\pi)^d \det({\Sigma})}} \exp\left( -\frac{1}{2} ({x}-{\mu})^\top {\Sigma}^{-1} ({x}-{\mu}) \right)N(x;μ,Σ)=(2π)ddet(Σ)1exp(−21(x−μ)⊤Σ−1(x−μ))(ddd是变量维度,μ{\mu}μ是均值向量,Σ{\Sigma}Σ是协方差矩阵);
- 均值与协方差:E[x]=μ\mathbb{E}[{x}]={\mu}E[x]=μ,Cov[x]=Σ\text{Cov}[{x}]={\Sigma}Cov[x]=Σ;
- 各向同性高斯分布:特殊情况,协方差矩阵Σ=αI{\Sigma} = \alpha {I}Σ=αI(α\alphaα是标量,I{I}I是单位矩阵),此时分布在各个方向的“分散程度”一致。
举例:同时研究“身高”和“体重”两个连续变量,它们的联合分布可服从多元正态分布——均值向量μ{\mu}μ包含“平均身高”和“平均体重”,协方差矩阵Σ{\Sigma}Σ描述身高与体重的相关性,以及各自的方差。
(7)贝叶斯定理:从“先验”到“后验”的更新
贝叶斯定理是“基于新数据更新原有认知”的核心工具,公式为:
P(x∣y)=P(y∣x)P(x)P(y)P(x|y) = \frac{P(y|x)P(x)}{P(y)}P(x∣y)=P(y)P(y∣x)P(x)
各部分含义:
- P(x)P(x)P(x):先验概率(已知数据前的认知,比如“疾病发病率1%”);
- P(y∣x)P(y|x)P(y∣x):似然(新数据对认知的支持度,比如“患病者检测阳性的概率90%”);
- P(y)P(y)P(y):证据(归一化因子,比如“所有人检测阳性的概率”);
- P(x∣y)P(x|y)P(x∣y):后验概率(更新后的认知,比如“检测阳性后真正患病的概率”)。
例子:疾病检测中,已知发病率P(x)=1%P(x)=1\%P(x)=1%,真阳性率P(y∣x)=90%P(y|x)=90\%P(y∣x)=90%,假阳性率P(y∣¬x)=5%P(y|\neg x)=5\%P(y∣¬x)=5%,则检测阳性后患病的概率为:
P(x∣y)=0.9×0.010.9×0.01+0.05×0.99≈15.5%P(x|y) = \frac{0.9 \times 0.01}{0.9 \times 0.01 + 0.05 \times 0.99} \approx 15.5\%P(x∣y)=0.9×0.01+0.05×0.990.9×0.01≈15.5%
这说明:即使检测阳性,也不一定患病,贝叶斯定理帮我们避免“误判”。
3. 优化:让模型“找到最优解”
深度学习的本质是“最小化损失函数”(比如预测值与真实值的差距),而优化算法就是“找到最小化损失的参数”的工具。
- 我们想最大化或最小化的函数称为目标函数
- 当最小化目标函数时,也可以称其为成本函数,损失函数或误差函数
- 函数y = f(x)的导数表示为f’(x) 或 dydx\frac{dy}{dx}dxdy,含义为f 在x 处的斜率或梯度
(1)梯度下降:最核心的优化算法
梯度下降的思想:沿着损失函数下降最快的方向(梯度的反方向)更新参数,公式为:
x′=x−η∇f(x)x' = x - \eta \nabla f(x)x′=x−η∇f(x)
- xxx:当前参数;
- η\etaη:学习率(步长,太大易震荡不收敛,太小收敛慢,常用0.001、0.01);
- ∇f(x)\nabla f(x)∇f(x):梯度(损失函数在xxx处的偏导数向量,是函数增长最快的方向)。
(2)临界点与挑战:局部最小 vs 全局最小
梯度为0的点称为“临界点”,但不一定是“全局最小”:
- 全局最小:整个函数的最低点(最优解);
- 局部最小:某个区域的最低点(次优解,但如果性能接近全局最小,也可接受);
- 鞍点:梯度为0但不是极值(比如f(x,y)=x2−y2f(x,y)=x^2 - y^2f(x,y)=x2−y2在(0,0)处,沿x轴是最小,沿y轴是最大,是鞍点)。
实际训练中,我们很难找到全局最小,但通过“批量梯度下降、动量、Adam”等改进算法,可以有效避开鞍点,找到性能良好的局部最小。
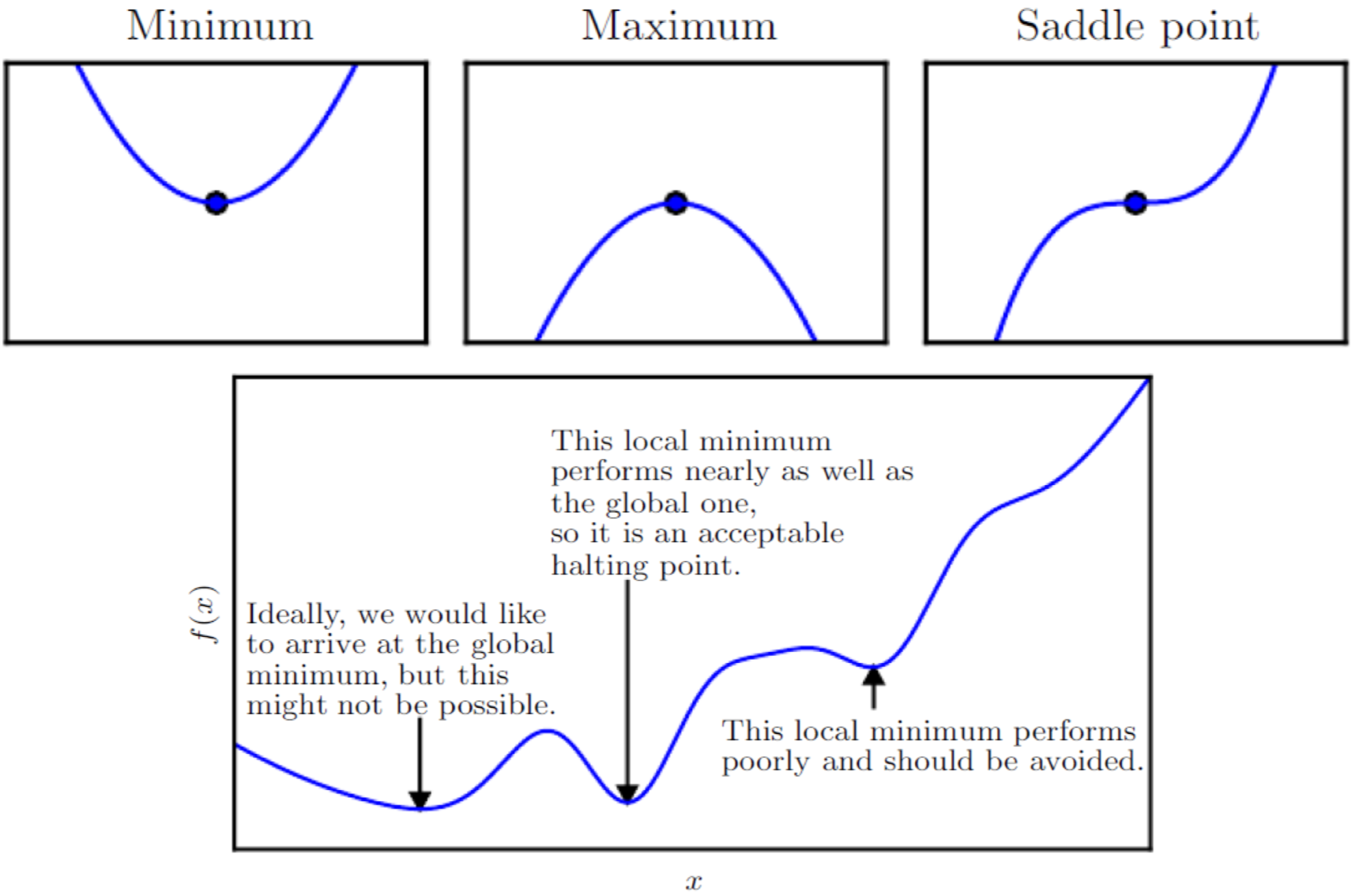
有一个单变量函数 (y = f(x)),目标是找到使 (f(x)) 最小的 x 值。此时梯度下降的更新规则为:x′=x−η⋅f′(x)x' = x - \eta \cdot f'(x)x′=x−η⋅f′(x)
符号解释:f’(x):函数 f(x) 对 x 的一阶导数,描述函数在 x 处的 “变化率”(斜率)。η\etaη(学习率):大于 0 的常数,控制每次更新的 “步长”—— 步长过大可能跳过最小值,步长过小则收敛极慢。
多变量函数的梯度是一个向量,整合了对所有变量的偏导数,记作 ∇xf(x)\nabla_{{x}} f({x})∇xf(x),形式为:
∇xf(x)=(∂f∂x1∂f∂x2⋮∂f∂xn) \nabla_{{x}} f({x}) = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{pmatrix} ∇xf(x)= ∂x1∂f∂x2∂f⋮∂xn∂f
既然梯度是“上升最快”的方向,那么“下降最快”的方向就是梯度的反方向。因此,多变量函数的梯度下降更新规则为:
$KaTeX parse error: Expected 'EOF', got '}' at position 2: x}̲' =$x} - \eta \…
- x{x}x、x′{x}'x′:n 维向量,分别代表“变量的当前值”和“更新后的值”。
- ∇xf(x)\nabla_{{x}} f({x})∇xf(x):梯度向量,指导“多维度下降的方向”。
- η\etaη:学习率,仍控制“步长”,平衡收敛速度与稳定性。
微积分运算法则
链式法则: 复合函数f(g(x)) 的导数
[f(g(x))]′=f′(g(x))g′(x)[f(g(x))]' = f'(g(x))g'(x)[f(g(x))]′=f′(g(x))g′(x)
莱布尼茨记法:
dzdx=dzdy⋅dydx\frac{dz}{dx} = \frac{dz}{dy} \cdot \frac{dy}{dx}dxdz=dydz⋅dxdy乘法法则: 两个函数相乘的导数
(f⋅g)′=f′⋅g+f⋅g′(f \cdot g)' = f' \cdot g + f \cdot g'(f⋅g)′=f′⋅g+f⋅g′
莱布尼茨记法:
ddx(u⋅v)=dudx⋅v+u⋅dvdx\frac{d}{dx}(u \cdot v) = \frac{du}{dx} \cdot v + u \cdot \frac{dv}{dx}dxd(u⋅v)=dxdu⋅v+u⋅dxdv除法法则
ddx(f(x)g(x))=f′g−fg′g2\frac{d}{dx}\left( \frac{f(x)}{g(x)} \right) = \frac{f'g - fg'}{g^2}dxd(g(x)f(x))=g2f′g−fg′
两步求导
输入层节点 中间层节点 输出层节点
x₁ ──┐ ┌─ u₁ ──┐ ┌─ w₁
x₂ ──┼──→ f₁───┘ └──→ g₁──┘
... │ ... ...
xₙ ──┘ └─ uₘ ──┐ └─ wₚ
└──→ gₚ──┘
假定我们有:
- 独立的输入变量:x1,x2,…,xnx_1, x_2, \dots, x_nx1,x2,…,xn
- 相关的中间变量:u1,u2,…,umu_1, u_2, \dots, u_mu1,u2,…,um,每一个中间变量都是 x1,x2,…,xnx_1, x_2, \dots, x_nx1,x2,…,xn 的函数
- 相关的输出变量:w1,w2,…,wpw_1, w_2, \dots, w_pw1,w2,…,wp,每一个输出变量都是 u1,u2,…,umu_1, u_2, \dots, u_mu1,u2,…,um 的函数
对于任意的 i∈{1,2,…,p}i \in \{1,2,\dots,p\}i∈{1,2,…,p} 和 j∈{1,2,…,n}j \in \{1,2,\dots,n\}j∈{1,2,…,n},可以推出多变量复合函数的链式法则:
∂wi∂xj=∑k=1m∂wi∂uk⋅∂uk∂xj\frac{\partial w_i}{\partial x_j} = \sum_{k=1}^{m} \frac{\partial w_i}{\partial u_k} \cdot \frac{\partial u_k}{\partial x_j}∂xj∂wi=∑k=1m∂uk∂wi⋅∂xj∂uk
∂wi∂xj=∂wi∂u1⋅∂u1∂xj+∂wi∂u2⋅∂u2∂xj+⋯+∂wi∂um⋅∂um∂xj\frac{\partial w_i}{\partial x_j} = \frac{\partial w_i}{\partial u_1} \cdot \frac{\partial u_1}{\partial x_j} + \frac{\partial w_i}{\partial u_2} \cdot \frac{\partial u_2}{\partial x_j} + \cdots + \frac{\partial w_i}{\partial u_m} \cdot \frac{\partial u_m}{\partial x_j}∂xj∂wi=∂u1∂wi⋅∂xj∂u1+∂u2∂wi⋅∂xj∂u2+⋯+∂um∂wi⋅∂xj∂um
两步求导公式正是神经网络 反向传播(Backpropagation 的数学基础 —— 它描述了 “输出对输入的梯度” 如何通过 “中间变量” 传递,而这种 “分层依赖结构” 就是反向传播能高效计算梯度的前提。
二、机器学习基础:让模型“从数据中学习”
有了数学基础,我们再看机器学习的核心逻辑:如何让计算机从数据中学习规律,并用规律解决实际问题。
1. 机器学习的“三要素”:任务(T)、经验(E)、评价(P)
Tom Mitchell在1997年给出了机器学习的经典定义:
“一个计算机程序从经验E中学习,针对任务T,用评价指标P衡量性能,若性能随E增加而提升,则称其为学习算法。”
我们用“房价预测”为例,拆解三要素:
- 任务T:根据“面积、地段、房龄”预测“房价”(回归任务);
- 经验E:1000条“面积、地段、房龄、房价”的历史数据(监督学习的标注数据);
- 评价P:预测房价与真实房价的均方误差(MSE),MSE越小,性能越好。
1.1 核心任务类型:从“预测”到“生成”
机器学习的任务本质是“对数据做什么”,常见任务分为以下几类:
| 任务类型 | 目标 | 例子 |
|---|---|---|
| 分类(Classification) | 输出离散类别(如1~k) | 图像识别(猫/狗/鸟)、垃圾邮件检测(垃圾/正常) |
| 回归(Regression) | 输出连续值 | 房价预测、股票价格预测、气温预测 |
| 生成(Generation) | 生成与真实数据相似的新数据 | GAN生成人脸、AI写文章、AI作曲 |
| 降噪(Denoising) | 去除数据中的噪声,恢复真实数据 | 老照片修复、语音降噪、图像去模糊 |
| 转录(Transcription) | 将非文本数据转为文本 | 语音转文字(ASR)、手写体识别 |
| 机器翻译(MT) | 将一种语言转为另一种语言 | 英文转中文、日文转英文 |
结构预测,异常检测,生成和采样,估算缺失值,密度估算…
1.2 经验
根据训练时使用的经验类型,机器学习(含深度学习)算法主要分为 无监督学习(unsupervised) 和 有监督学习(supervised) 两类。
算法的学习经验以数据集的形式提供,数据集是“样本(或数据点)”的集合。每个样本/数据点通常用向量x{x}x 表示,可视为“随机变量 x{x}x”的一次采样(即从真实数据分布中抽取的一个实例)。
无监督学习的数据集仅包含特征(无额外标签),算法目标是发现数据内在的属性或结构(比如分布规律、聚类模式等)。
- 核心目标的数学表达:学习“样本 x{x}x 的概率分布”,即learn p(x)\text{learn } p({x})learn p(x)。
- 举例:
- 聚类任务:将客户消费数据(特征为“消费金额、消费频率”等)自动分成“高活跃客户群”“中等活跃客户群”“低活跃客户群”,无需提前给每个客户标注“群体标签”。
- 降维任务:把高维的图像像素特征(如1000维)压缩到低维(如2维),同时尽可能保留图像的核心区分信息,过程中不需要“低维标签”指导。
有监督学习的数据集既有特征,又有每个样本对应的标签/目标(用yyy 表示),算法目标是学习“特征xxx到标签yyy”的映射关系。
- 核心目标的数学表达:学习“给定样本xxx 时,标签yyy的条件概率分布”,即 learn p(y∣x)\text{learn } p({y}|{x})learn p(y∣x)。
- 举例:
- 图像分类:数据集里每张图片(特征是像素值 x{x}x)都标注了“类别标签 y{y}y”(如“猫”“狗”),算法学习“根据图片像素判断类别”的能力。
- 房价预测:数据集里每套房子的“面积、地段等特征 x{x}x”都对应“房价标签 y{y}y”,算法学习“从房子特征预测房价”的规则。
1.3 评价指标
- 评价指标需要可以定量评估机器学习(ML)系统的性能
- 评价指标P 通常取决于系统要执行的任务T
- 分类和转录: 准确率或错误率
- 回归和降噪: 预测与真实之间的距离
- 生成,机器翻译: 比较困难,有时需要人类评估
- 评价指标是系统在**测试集 (test set)**上的性能度量,测试集与用于训练系统的训练集是分离的
1.4 示例:线性回归
任务TTT: 用x{x}x 预测yyy,y^=w⊤x\hat{y} = {w}^\top {x}y^=w⊤x
评价指标PPP: 模型在包含mmm 个测试样本{(xi,yi)}test\{({x}_i, y_i)\}^\text{test}{(xi,yi)}test 的测试集上的均方误差
MSEtest=1m∑i(y^i−yi)test \text{MSE}_\text{test} = \frac{1}{m} \sum_{i} (\hat{y}_i - y_i)^\text{test} MSEtest=m1i∑(y^i−yi)test经验EEE: 最小化模型在包含qqq 个训练样本{(xi,yi)}train\{({x}_i, y_i)\}^\text{train}{(xi,yi)}train 的训练集上的均方误差
MSEtrain=1q∑i(y^i−yi)train \text{MSE}_\text{train} = \frac{1}{q} \sum_{i} (\hat{y}_i - y_i)^\text{train} MSEtrain=q1i∑(y^i−yi)train- 令{(xi,yi)}train\{({x}_i, y_i)\}^\text{train}{(xi,yi)}train 整体表示为(Xtrain,ytrain)({X}^\text{train}, {y}^\text{train})(Xtrain,ytrain),则
∇wMSEtrain=∇w1q∥y^train−ytrain∥22=0 \nabla_{{w}} \text{MSE}_\text{train} = \nabla_{{w}} \frac{1}{q} \|\hat{{y}}^\text{train} - {y}^\text{train}\|_2^2 = 0 ∇wMSEtrain=∇wq1∥y^train−ytrain∥22=0
可求出:
w=(Xtrain⊤Xtrain)−1Xtrain⊤ytrainw = \left( X_{\text{train}}^\top X_{\text{train}} \right)^{-1} X_{\text{train}}^\top y_{\text{train}} w=(Xtrain⊤Xtrain)−1Xtrain⊤ytrain
- 令{(xi,yi)}train\{({x}_i, y_i)\}^\text{train}{(xi,yi)}train 整体表示为(Xtrain,ytrain)({X}^\text{train}, {y}^\text{train})(Xtrain,ytrain),则
3. 容量、过拟合与欠拟合:模型“泛化能力”的关键
机器学习的终极目标是“在新数据上表现好”(泛化能力强),而泛化能力的核心是“模型容量与数据复杂度匹配”。
模型容量,也称为表达能力(Expressive Power),指的是一个机器学习模型(如深度神经网络)能够拟合各种复杂函数(或数据分布)的能力。
- 模型容量:模型拟合复杂数据的能力(比如线性模型容量低,9次多项式模型容量高);
- 欠拟合:模型容量不足,连训练数据都拟合不好(比如用线性模型拟合非线性的房价数据,训练误差大);
- 过拟合:模型容量过高,记住了训练数据的噪声,在新数据上表现差(比如用9次多项式拟合简单的房价数据,训练误差小但测试误差大)。
如何判断欠拟合/过拟合?
- 欠拟合:训练误差大,测试误差也大;
- 过拟合:训练误差小,测试误差大。
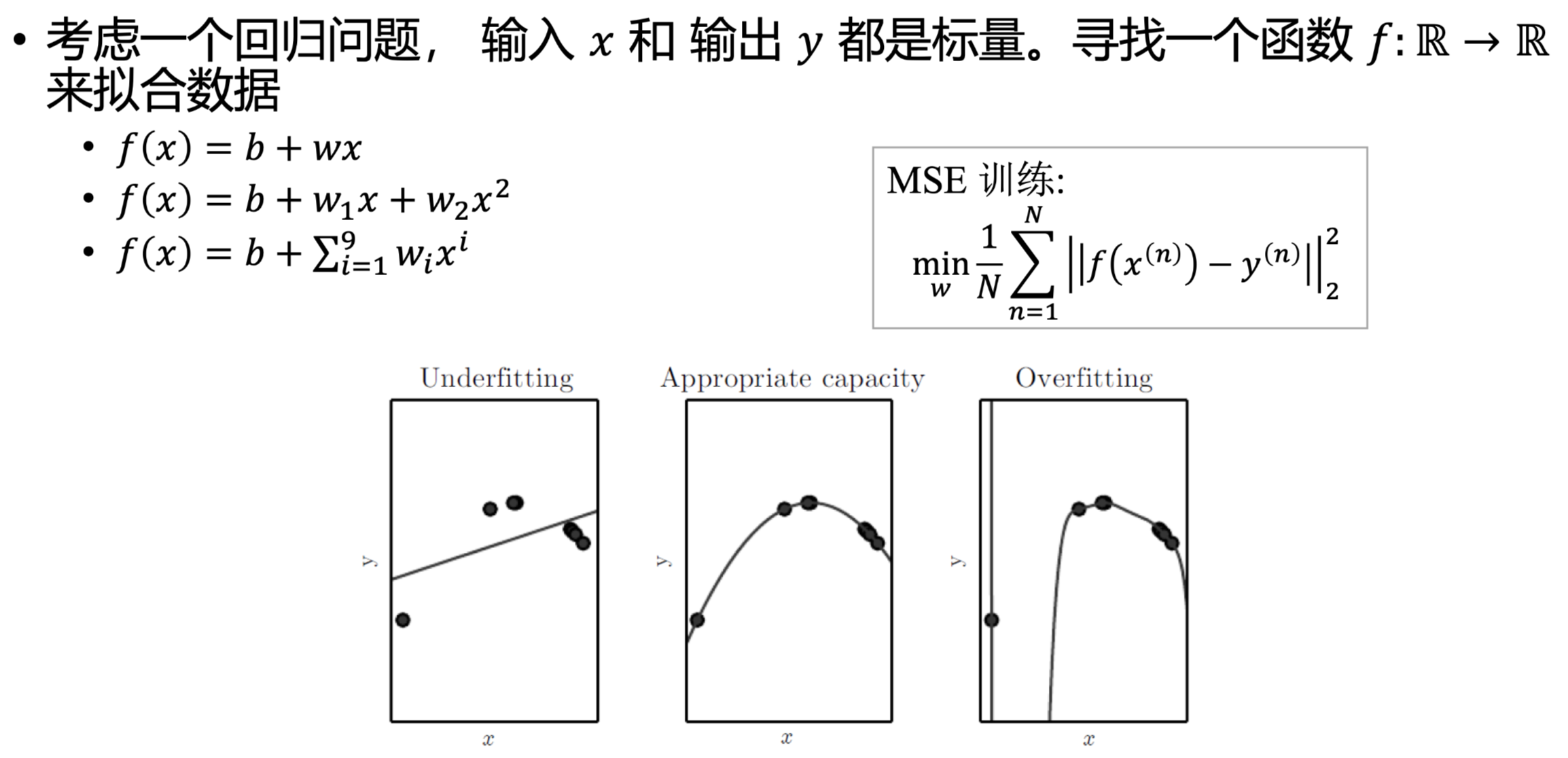
1.增大模型容量 → 减小训练误差 模型容量决定了其拟合复杂数据分布的能力。当模型容量不足时(比如用简单线性模型处理“高度非线性”的任务,如图像分类、自然语言理解),它无法充分捕捉训练数据中的内在规律,会导致训练误差较高(模型连训练数据的基本模式都没学会,即“欠拟合”)。
通过增大模型容量(如加深网络层数、加宽层内神经元/卷积核数量、增加参数总量等),模型的“表达能力”会增强,能更精准地拟合训练数据的分布(甚至学习到更细致的特征),从而有效减小训练误差。
2.增强泛化能力 → 缩小训练误差和测试误差之间的差距 泛化能力指模型对未见过的测试数据的预测能力。如果模型容量过高且缺乏约束,会过度拟合训练数据中的“噪声”(而非数据的“通用规律”),此时会出现训练误差很低,但测试误差很高的情况(即“过拟合”,训练与测试误差的差距被拉大)。
“增强泛化能力”的核心,是让模型学到更具普遍性的规律(而非训练数据的“专属特性”)。通过正则化(如Dropout、L2权重衰减)、数据增强(生成更多多样化训练样本)、早停(在测试误差上升前停止训练)等手段,可限制模型对“噪声”的过度学习,使模型更“鲁棒”,从而缩小训练误差与测试误差的差距,让模型在新数据上也能表现良好。
4. 正则化:防止过拟合的“利器”
正则化是我们旨在减少模型泛化误差而不是训练误差,从而对学习算法所做的任何修改。从技术角度看,过拟合的本质是模型容量过剩:模型太复杂,不仅学到了数据的 “通用规律”,还把训练数据里的 “噪声”(比如个别样本的特殊标记、无关背景)也当成了 “规律” 来学习。
正则化要做的是 “平衡术”:既让模型有能力拟合数据(别欠拟合),又不让它 “过度放飞” 去学噪声(别过拟合)。这背后是深度学习的经典理论 ——偏差 - 方差权衡:
偏差高:模型太简单,连训练数据的规律都没学好(欠拟合);
方差高:模型太复杂,学了训练数据的噪声,对新数据泛化差(过拟合);
正则化的作用:通过限制模型复杂度,让 “偏差” 和 “方差” 达到平衡。
常见正则化方法大起底
正则化不是“单一方法”,而是一套“策略集合”。下面介绍最常用的几种“武器”:
1. 权重衰减(L2正则化):给权重“减减肥”
公式:修改损失函数,加入“权重的平方和”惩罚项:
J(w)=MSEtrain+λ⋅w⊤w J(w) = \text{MSE}_{\text{train}} + \lambda \cdot w^\top w J(w)=MSEtrain+λ⋅w⊤w
- MSEtrain\text{MSE}_{\text{train}}MSEtrain:训练数据的损失(比如均方误差);
- www:模型的权重参数(如神经网络的连接权重);
- λ\lambdaλ:正则化强度(超参数,需要手动调)。
原理:λ\lambdaλ越大,“惩罚权重平方和”的力度越强,迫使权重尽量“变小”。从梯度下降的角度看,L2正则化会让权重更新时额外减去一项 2λw2\lambda w2λw——这相当于每次更新都把权重往“0”的方向“拉一把”,防止权重变得过大、过于“极端”。
效果:让模型的预测更“平滑”(不会因为个别样本的微小变化就剧烈波动),从而减少对训练噪声的依赖。
2. L1正则化:给权重“做减法”(稀疏化)
L1正则化的损失函数形式为:
J(w)=Ltrain(w)+λ∥w∥1 J(w) = L_{\text{train}}(w) + \lambda \|w\|_1 J(w)=Ltrain(w)+λ∥w∥1
其中 ∥w∥1=∑i=1n∣wi∣\|w\|_1 = \sum_{i=1}^n |w_i|∥w∥1=∑i=1n∣wi∣(所有权重的绝对值之和),λ\lambdaλ是正则化强度。
梯度更新:“常数力”推权重向0
对损失函数 J(w)J(w)J(w)关于权重 wiw_iwi求梯度(次梯度,因绝对值在0点不可导):
∂J∂wi=∂Ltrain∂wi+λ⋅sign(wi) \frac{\partial J}{\partial w_i} = \frac{\partial L_{\text{train}}}{\partial w_i} + \lambda \cdot \text{sign}(w_i) ∂wi∂J=∂wi∂Ltrain+λ⋅sign(wi)
其中 sign(wi)\text{sign}(w_i)sign(wi)是符号函数:wi>0w_i>0wi>0时为 +1,+1,+1,wi<0w_i<0wi<0时为 −1-1−1,wi=0w_i=0wi=0时为 000
- 关键差异:L1正则化的梯度是常数(±λ\pm\lambda±λ),与权重大小无关;而L2正则化的梯度是 2λwi2\lambda w_i2λwi(与权重大小成正比)。
- 更新行为:在梯度下降中,L1的“拉零力”是固定强度的。对于小权重(接近0的权重),原始损失的梯度(拟合数据的“推动力”)可能不足以抵消L1的“拉零力”,导致权重被直接推至0。
特点:L1正则化会让大量权重变成0,产生“稀疏权重”。这相当于自动帮模型做“特征选择”——只保留最关键的特征,抛弃无用特征。
对比L2:L2是“让权重变小但不全为0”,L1是“让大量权重直接为0”。如果你的任务需要特征选择(比如输入特征很多,想找出关键特征),L1更适合。
3. Dropout:让模型“随机失忆”
操作:训练时,随机“关闭”一部分神经元(比如每次训练随机让50%的神经元不工作);测试时,再把所有神经元“打开”。
原理:训练时,模型每次都要“换一种结构”(因为不同神经元被随机关闭),无法依赖某几个“核心神经元”;这迫使模型学习更鲁棒、通用的特征(毕竟下次这几个神经元可能就“失忆”了)。测试时,相当于把“无数个不同结构的子模型”的预测结果做了一次“平均”,减少了模型的“方差”(对新数据的波动)。
比喻:训练时,模型是“一个团队,每天随机有人请假”,所以每个人都得学会独立干活;测试时,“所有人都到岗”,效率自然更高。
4. 早停(Early Stopping):及时喊“停”的智慧
操作:训练过程中,持续监控验证集的误差;当验证集误差“不再下降,甚至开始上升”时,立刻停止训练。
原理:过拟合发生时,“训练误差”还在下降(模型还在学训练数据的细节),但“验证误差”已经开始上升(模型对新数据的泛化能力下降)。早停相当于在模型“刚要过拟合”时踩刹车,保留此时泛化能力最好的模型。
特点:简单粗暴但极其有效,是深度学习最常用的正则化手段之一。
5. 数据增强:给模型“多看世界”
操作:通过“人工生成新数据”来扩充训练集。比如:
- 图像任务:翻转、裁剪、调整亮度/对比度、加噪声;
- 文本任务:同义词替换、随机插入/删除单词;
- 语音任务:改变语速、添加背景噪音。
原理:模型见的“数据变化”越多,就越难“死记”个别样本的特征(因为样本太多变了),只能去学“更通用的规律”。相当于让模型“见多识广”,自然更能“触类旁通”。
正则化的实践:超参数的博弈
正则化的效果,很大程度取决于超参数的选择(比如L2的λ\lambdaλ、Dropout的“丢弃率”、早停的“等待轮数”)。不同任务、不同模型,适合的超参数天差地别:
L2的λ\lambdaλ:简单任务(如线性数据拟合)可以选小λ\lambdaλ;复杂任务(如大模型图像分类)可能需要大λ\lambdaλ,但要防止“欠拟合”。
Dropout丢弃率:
计算机视觉任务:Dropout 丢弃率常用 0.2~0.5(视觉特征相对更 “局部”,随机丢弃部分神经元对整体特征学习影响可控,能有效增强鲁棒性)。
自然语言处理任务(如 Transformer):Dropout 丢弃率常用 0.1~0.3(文本依赖序列的全局语义关联,若丢弃过多神经元,会破坏序列信息的连贯性,因此需降低丢弃比例以保留更多语义线索)。早停的patience:
早停的核心是监控验证集性能(如损失、准确率):当验证集指标连续 patience 轮不再提升时,停止训练。
patience 越大,允许验证集 “连续多少轮不提升” 的容忍度越高;
patience 越小,对 “验证集不提升” 的反应越敏感。
当数据波动大时(如验证集规模小、数据噪声多、未做数据增强),验证集的指标(如损失、准确率)会因随机波动出现 “暂时性下降”—— 此时模型并未真的过拟合,只是验证数据的噪声导致指标波动。
若 patience 太小(如 3 轮),一旦验证指标因波动下降,就会误判为 “过拟合” 而提前停止训练,错过后续可能的提升;
若 patience 增大(如 10 轮),可以 “容忍” 更多轮的波动,确保只有当验证指标持续下降(真的过拟合)时才停止。
当数据稳定时(如验证集规模大、数据增强充分、样本分布均匀),验证集指标的波动很小 —— 此时指标下降更可能是真的过拟合(模型开始学习训练数据的噪声)。
若 patience 太大(如 20 轮),会让模型在过拟合状态下继续训练,浪费计算资源;
若 patience 减小(如 5 轮),可以在验证指标刚出现 “停滞 / 下降” 的早期就停止训练,及时 “刹车”。
技巧:用交叉验证(把数据分成多份,轮流当验证集)来选择最优超参数,能大大提高正则化的效果。
正则化的本质:限制模型容量
回到“模型容量”的概念:正则化其实是在主动限制模型的容量,防止模型因为“太复杂”而过拟合。
- L2/L1:通过限制权重的大小/数量,减少模型的“自由度”;
- Dropout:训练时用“更小的子模型”,间接降低容量;
- 早停:在模型还没“长到过于复杂”时停止训练;
- 数据增强:相当于“用更多数据支撑高容量模型”,让模型有足够的数据去学通用规律,而不是噪声。
所以,“增大模型容量(提升拟合能力)”和“正则化(限制容量防过拟合)”是深度学习的“左右手”——只有配合好,才能让模型既“学得会”,又“考得好”。
5. 超参数与验证集:如何“调优模型”
机器学习模型有两类参数:
- 可学习参数:从数据中学习的参数(如线性回归的权重www、偏置bbb);
- 超参数:手动设置的参数(如正则化强度λ\lambdaλ、学习率η\etaη、神经网络层数、每层神经元个数),不会被算法更新,超参数通常决定了模型的容量,需通过验证集调优。
验证集的作用是“选择超参数”,数据集通常分为三部分:
- 训练集(70%~80%):训练模型,更新可学习参数;
- 验证集(10%~15%):调整超参数,选择最优模型;
- 测试集(10%~15%):最终评估模型泛化能力,绝对不能用于调参。
若数据量小,可采用“k折交叉验证”:将训练集分成k份,每次用k-1份训练,1份验证,重复k次,取平均性能作为超参数的评价指标(常用k=5或10)。
6. 最大似然估计(MLE):模型“学习”的数学基础
一、最大似然估计(Maximum Likelihood Estimation, MLE)
核心思想:找到一组模型参数,使得“观测到当前这组数据”的概率最大。
1. 问题定义
- 已知:有NNN 个独立同分布(i.i.d.)的样本X={x(1),x(2),...,x(N)}\mathbb{X} = \{x^{(1)}, x^{(2)}, ..., x^{(N)}\}X={x(1),x(2),...,x(N)},每个样本都来自未知的真实数据分布pdata(x)p_{\text{data}}(x)pdata(x)。
- 目标:找一个模型分布pmodel(x;θ)p_{\text{model}}(x; \theta)pmodel(x;θ)(由参数θ\thetaθ 控制,比如高斯分布的均值/方差),让模型尽可能近似真实分布pdata(x)p_{\text{data}}(x)pdata(x)。
2. 公式推导:从“联合概率”到“对数似然”
因为样本独立同分布,“模型生成所有NNN 个样本”的联合概率(似然)是每个样本概率的乘积:
pmodel(X;θ)=∏i=1Npmodel(x(i);θ)p_{\text{model}}(\mathbb{X}; \theta) = \prod_{i=1}^{N} p_{\text{model}}(x^{(i)}; \theta)pmodel(X;θ)=∏i=1Npmodel(x(i);θ)
最大似然估计的目标是找θ\thetaθ 使这个联合概率最大:
θML=argmaxθpmodel(X;θ)⏟似然函数\theta_{\text{ML}} = \arg\max_{\theta} \underbrace{p_{\text{model}}(\mathbb{X}; \theta)}_{\text{似然函数}}θML=argmaxθ似然函数
pmodel(X;θ)
但“连乘”计算不便(如数值下溢、求导复杂),因此对似然函数取对数(对数是单调递增函数,最大化对数似然等价于最大化原似然),将“连乘”转化为“求和”:
θML=argmaxθ∑i=1Nlogpmodel(x(i);θ)\theta_{\text{ML}} = \arg\max_{\theta} \sum_{i=1}^{N} \log p_{\text{model}}(x^{(i)}; \theta)θML=argmaxθ∑i=1Nlogpmodel(x(i);θ)
当样本足够多时,经验分布p^data\hat{p}_{\text{data}}p^data(样本的频率分布)近似真实分布pdatap_{\text{data}}pdata,因此对数似然可表示为期望形式:
θML=argmaxθEx∼p^datalogpmodel(x;θ)\theta_{\text{ML}} = \arg\max_{\theta} \mathbb{E}_{x \sim \hat{p}_{\text{data}}} \log p_{\text{model}}(x; \theta)θML=argmaxθEx∼p^datalogpmodel(x;θ)
3. 例子:抛硬币(伯努利分布的参数估计)
假设抛硬币,“正面(记为1)”的概率为θ\thetaθ,“反面(记为0)”的概率为1−θ1-\theta1−θ。现在抛5次,得到样本:( x = [1, 1, 1, 0, 1](4次正面,1次反面)。
- 模型选择:用伯努利分布建模单次抛硬币的结果,即pmodel(x;θ)=θx(1−θ)1−xp_{\text{model}}(x; \theta) = \theta^x (1-\theta)^{1-x}pmodel(x;θ)=θx(1−θ)1−x(( x=1时概率为θ\thetaθ,( x=0时为1−θ1-\theta1−θ)。
- 似然函数:5个独立样本的联合概率(似然)为:
L(θ)=pmodel([1,1,1,0,1];θ)=θ1⋅θ1⋅θ1⋅(1−θ)1⋅θ1=θ4(1−θ)1\mathcal{L}(\theta) = p_{\text{model}}([1,1,1,0,1]; \theta) = \theta^1 \cdot \theta^1 \cdot \theta^1 \cdot (1-\theta)^1 \cdot \theta^1 = \theta^4 (1-\theta)^1L(θ)=pmodel([1,1,1,0,1];θ)=θ1⋅θ1⋅θ1⋅(1−θ)1⋅θ1=θ4(1−θ)1 - 对数似然:取对数(将连乘转求和,简化计算):
logL(θ)=4logθ+1log(1−θ)\log \mathcal{L}(\theta) = 4 \log \theta + 1 \log (1-\theta)logL(θ)=4logθ+1log(1−θ) - 最大化对数似然:对θ\thetaθ 求导并令导数为0,解得:
ddθlogL(θ)=4θ−11−θ=0 ⟹ θ=45=0.8\frac{d}{d\theta} \log \mathcal{L}(\theta) = \frac{4}{\theta} - \frac{1}{1-\theta} = 0 \implies \theta = \frac{4}{5} = 0.8dθdlogL(θ)=θ4−1−θ1=0⟹θ=54=0.8
结果符合直觉:抛5次有4次正面,最大似然估计的“正面概率”就是正面出现的频率。
二、条件对数似然(Conditional Log-Likelihood)
核心思想:在“给定输入xxx,预测输出yyy”的监督任务中,找到参数使“观测到标签yyy(给定xxx)”的概率最大。
1. 问题定义
- 任务:给定输入xxx,预测输出yyy(如分类中yyy 是标签,回归中yyy 是连续值)。
- 目标:估计条件概率p(y∣x;θ)p(y|x; \theta)p(y∣x;θ),并找到参数θ\thetaθ 使得“观测到的(x,y)(x, y)(x,y) 对”的联合概率最大。
2. 公式推导:从“条件联合概率”到“条件对数似然”
假设所有样本{(x(1),y(1)),...,(x(N),y(N))}\{(x^{(1)}, y^{(1)}), ..., (x^{(N)}, y^{(N)})\}{(x(1),y(1)),...,(x(N),y(N))} 独立同分布,“模型生成所有标签YYY(给定输入XXX)”的条件联合概率是每个样本条件概率的乘积:
Pmodel(Y∣X;θ)=∏i=1NPmodel(y(i)∣x(i);θ)P_{\text{model}}(Y|X; \theta) = \prod_{i=1}^{N} P_{\text{model}}(y^{(i)}|x^{(i)}; \theta)Pmodel(Y∣X;θ)=∏i=1NPmodel(y(i)∣x(i);θ)
条件最大似然估计的目标是找θ\thetaθ 最大化这个条件联合概率,同样取对数(连乘转求和):
θML=argmaxθ∑i=1NlogPmodel(y(i)∣x(i);θ)\theta_{\text{ML}} = \arg\max_{\theta} \sum_{i=1}^{N} \log P_{\text{model}}(y^{(i)}|x^{(i)}; \theta)θML=argmaxθ∑i=1NlogPmodel(y(i)∣x(i);θ)
3. 例子:手写数字分类(Softmax回归)
用Softmax回归做“手写数字分类”(10类,数字0-9),每个样本是“图像特征x(i)x^{(i)}x(i)”和“标签y(i)y^{(i)}y(i)”(如y=3y=3y=3 表示数字3)。
- 模型选择:用Softmax函数建模“给定图像xxx 时,类别y=ky=ky=k 的条件概率”:
Pmodel(y=k∣x;θ)=exp(θkTx)∑j=09exp(θjTx)P_{\text{model}}(y=k|x; \theta) = \frac{\exp(\theta_k^T x)}{\sum_{j=0}^{9} \exp(\theta_j^T x)}Pmodel(y=k∣x;θ)=∑j=09exp(θjTx)exp(θkTx)
其中θ={θ0,θ1,...,θ9}\theta = \{\theta_0, \theta_1, ..., \theta_9\}θ={θ0,θ1,...,θ9} 是模型参数(每个类别对应一组权重)。 - 对数似然:对于NNN 个训练样本,条件对数似然为:
∑i=1NlogPmodel(y(i)∣x(i);θ)\sum_{i=1}^{N} \log P_{\text{model}}(y^{(i)}|x^{(i)}; \theta)∑i=1NlogPmodel(y(i)∣x(i);θ) - 训练目标:最大化这个对数似然(实际中常转化为“最小化负对数似然”,即交叉熵损失),从而得到最优参数θ\thetaθ,让模型对训练样本的分类概率尽可能大。
三、两者的联系与区别
| 对比项 | 最大似然估计(MLE) | 条件对数似然 |
|---|---|---|
| 任务类型 | 无监督(拟合p(x)p(x)p(x)) | 监督(拟合$p(y |
| 核心目标 | 让“模型生成观测xxx 的概率最大” | 让“模型给定xxx 时生成yyy 的概率最大” |
| 公式核心 | argmaxθ∑logp(x;θ)\arg\max_{\theta} \sum \log p(x; \theta)argmaxθ∑logp(x;θ) | $\arg\max_{\theta} \sum \log p(y |
| 联系 | 条件对数似然是“MLE在条件概率场景下的延伸”;都通过“最大化对数似然”估计参数,且利用“独立同分布样本的联合概率可分解”的性质 |
简言之,最大似然估计是无监督学习的理论基础,而条件对数似然是监督学习(分类、回归等)的理论基础,两者都遵循“让观测数据的概率(或条件概率)最大”的核心逻辑。
7. 随机梯度下降(SGD):大规模数据的“训练神器”
1. 背景:为什么需要“随机梯度下降”?
训练机器学习模型时,核心是最小化成本函数(损失函数),而最小化的方法是通过梯度下降:沿着成本函数的“梯度反方向”更新参数,逐步找到最小值。
但直接用**全部训练集(批量梯度下降,Batch GD)**存在问题:
- 若训练集很大(比如百万级样本),每次计算“全量样本的梯度”会消耗极大的计算资源(时间、内存),甚至硬件无法支撑。
2. 梯度下降的三种方式(对比理解)
为解决“批量梯度下降”的效率问题,衍生出随机梯度下降和小批量梯度下降(是SGD的常用变体,也是图中重点)。
| 类型 | 每次用多少样本计算梯度? | 优点 | 缺点 |
|---|---|---|---|
| 批量梯度下降(Batch GD) | 全部训练集 | 梯度最准确,收敛稳定 | 计算开销极大,速度慢 |
| 随机梯度下降(SGD) | 1个样本 | 计算极快,迭代效率高 | 梯度波动大,收敛路径曲折 |
| 小批量梯度下降(Mini-batch SGD) | 一小批样本(如32、64、128个) | 平衡“计算效率”和“梯度稳定性” | 需调整“批量大小”超参数 |
3. “小批量随机梯度下降”的详细解释
小批量梯度下降(属于SGD的范畴,是工业界最常用的方式),核心是“把训练集拆成多个小批量(minibatches),用每个小批量的梯度近似全量梯度”。
(1)核心思想
将大规模训练集划分为若干小批量(minibatch),每次只对一个小批量计算损失和梯度,再通过“多个小批量的平均梯度”更新参数——既减少了单次计算量,又让梯度更稳定(比“单样本SGD”波动小)。
(2)公式解析
成本函数(损失的平均值):
J(θ)=1N′∑i=1N′L(X(i),y(i),θ)J(\theta) = \frac{1}{N'} \sum_{i=1}^{N'} L(X^{(i)}, y^{(i)}, \theta)J(θ)=N′1∑i=1N′L(X(i),y(i),θ)
其中:- N′N'N′:小批量的总数量;
- (X(i),y(i))(X^{(i)}, y^{(i)})(X(i),y(i)):第iii个小批量的“特征-标签”数据;
- L(⋅)L(\cdot)L(⋅):单个小批量的损失函数(如均方误差、交叉熵等);
- θ\thetaθ:模型参数(如线性回归的权重、神经网络的权重和偏置)。
含义:整个训练集的成本,是所有小批量损失的平均值。
梯度计算(成本函数对参数的偏导):
g=1N′∇θ∑i=1N′L(X(i),y(i),θ){g} = \frac{1}{N'} \nabla_{\theta} \sum_{i=1}^{N'} L(X^{(i)}, y^{(i)}, \theta)g=N′1∇θ∑i=1N′L(X(i),y(i),θ)
含义:成本函数对参数θ\thetaθ的梯度,是“所有小批量损失的梯度”的平均值。参数更新:
θ=θ−ηg\theta = \theta - \eta {g}θ=θ−ηg
其中η\etaη是学习率(控制每次参数更新的步长)。
含义:沿着“梯度的反方向”调整参数,让成本函数逐步减小(因为梯度指向“上升最快的方向”,减梯度就指向“下降最快的方向”)。
(3)小批量的超参数
图中补充:
- “共N′N'N′个minibatches”:训练集被拆分为N′N'N′个小批量,遍历所有小批量为一个epoch(轮次)。
- “minibatches的大小可以取1到几百”:
- 取1 → 就是“纯随机梯度下降(SGD)”;
- 取“全部训练集大小” → 就是“批量梯度下降(Batch GD)”;
- 工业界常用32、64、128、256等(需根据硬件内存、任务特性调优)。
4. 举例:用“房价预测(线性回归)”理解
假设要训练一个线性回归模型,预测房价:
- 特征:房屋面积、卧室数量等;
- 标签:房价;
- 训练集:共10000个样本。
(1)批量梯度下降(对比)
每次用全部10000个样本计算损失:
损失函数(均方误差):Lbatch=110000∑j=110000(yj−y^j)2L_{\text{batch}} = \frac{1}{10000} \sum_{j=1}^{10000} (y_j - \hat{y}_j)^2Lbatch=100001∑j=110000(yj−y^j)2(y^j=θ0+θ1xj1+θ2xj2+...\hat{y}_j = \theta_0 + \theta_1 x_{j1} + \theta_2 x_{j2} + ...y^j=θ0+θ1xj1+θ2xj2+...是预测值)。
然后计算梯度∇θLbatch\nabla_{\theta} L_{\text{batch}}∇θLbatch,更新参数θ\thetaθ。
→ 问题:10000个样本计算量极大,假设每个样本计算需0.1ms,单次梯度计算要1秒,训练速度极慢。
(2)小批量梯度下降(图中方式)
把10000个样本拆成小批量(如每个批量含64个样本):
总小批量数N′=10000÷64≈157N' = 10000 \div 64 \approx 157N′=10000÷64≈157。
对第iii个小批量(含64个样本):
- 计算该批量的损失:L(i)=164∑k=164(yk−y^k)2L^{(i)} = \frac{1}{64} \sum_{k=1}^{64} (y_k - \hat{y}_k)^2L(i)=641∑k=164(yk−y^k)2;
- 计算该批量的梯度:∇θL(i)\nabla_{\theta} L^{(i)}∇θL(i);
遍历所有157个小批量后,计算平均梯度:
g=1157∑i=1157∇θL(i){g} = \frac{1}{157} \sum_{i=1}^{157} \nabla_{\theta} L^{(i)}g=1571∑i=1157∇θL(i);
最后更新参数:θ=θ−ηg\theta = \theta - \eta {g}θ=θ−ηg。
→ 优势:单次只需处理64个样本(计算时间约6.4ms),比批量GD的1秒快得多;同时,64个样本的梯度比“1个样本”更稳定,收敛更平滑。
三、总结:基础不牢,地动山摇
深度学习看似复杂,但剥开层层包装后,核心还是“数学基础+机器学习逻辑”:
- 线性代数帮我们“结构化表示数据”,是模型输入的载体;
- 概率论帮我们“量化不确定性”,是损失函数和模型假设的依据;
- 优化算法帮我们“找到最优参数”,是模型学习的动力;
- 机器学习的三要素、泛化能力、正则化等概念,是“让模型有用”的关键。
如果你是深度学习初学者,建议先从“实现线性回归”开始:用NumPy实现向量乘法、梯度下降,观察过拟合与正则化的效果,再逐步学习更复杂的模型。基础打扎实了,后续学习CNN、RNN、Transformer时,才能真正理解“为什么这么设计”,而不是停留在“调参工具人”的阶段。
深度学习的路很长,但打好基础,每一步都会走得更稳。一起加油吧!