一、人话引入:ResNet 是个啥?
想象一下,你在学做一道超级复杂的菜,比如“佛跳墙”。

传统的深度学习网络:就像一个死记硬背的学徒。师傅告诉他,必须严格按照步骤来:先处理A食材,再处理B,然后炖C,最后加D。如果步骤(网络层数)太多太深,他学到后面可能就蒙逼了:“我丢,我第一步是啥来着?为啥第三步要那样做?” 结果就是,他不仅没学会新菜,连之前会的炒青菜(简单特征)都忘了。这在神经网络里叫做退化问题(Degradation Problem):网络不是越深越好,深到一定程度,准确率不升反降
ResNet(残差网络):就像一个聪明的学徒。他也在学“佛跳墙”,但他桌上始终摆着一盘做好的“高汤”(输入信号)。他每进行一步操作,都会时不时尝一口原来的高汤,思考:“我这一步操作,让高汤发生了多少变化(残差)?” 他的目标不是直接做出一整锅新汤,而是学习如何对现有的汤进行“微调”和“升级”。这样,即使步骤极其繁琐,他也能保证大方向不会错,最终做出来的汤至少不会比原来的高汤差。
这个“尝一口原来高汤”的操作,在ResNet里就叫快捷连接(Shortcut Connection)或跳远连接(Skip Connection)。它让信息可以直接从网络的浅层“跳”到深层,避免了在深层网络中“迷路”。
二、为什么要有 ResNet?(要解决什么问题?)
在ResNet出现之前,大家的共识是:网络越深,能提取的特征越复杂,模型性能应该越好。
但现实很骨感,人们发现当网络深度(层数)增加到一定程度(比如20层以上)时,会出现两个严重问题:
梯度消失/爆炸(Vanishing/Exploding Gradients):这是老生常谈了。误差反向传播时,梯度要经过很多层,每经过一层都可能被放大或缩小一点。层数太多,梯度可能变得极小(消失)或极大(爆炸),导致浅层的网络参数无法被有效更新。(这个问题通过权重初始化、BN层等技巧一定程度上可以缓解)
网络退化(Degradation):这是ResNet要解决的核心问题。即使解决了梯度消失,人们发现:一个56层的网络,其在训练集和测试集上的误差,竟然比一个20层的网络还要高
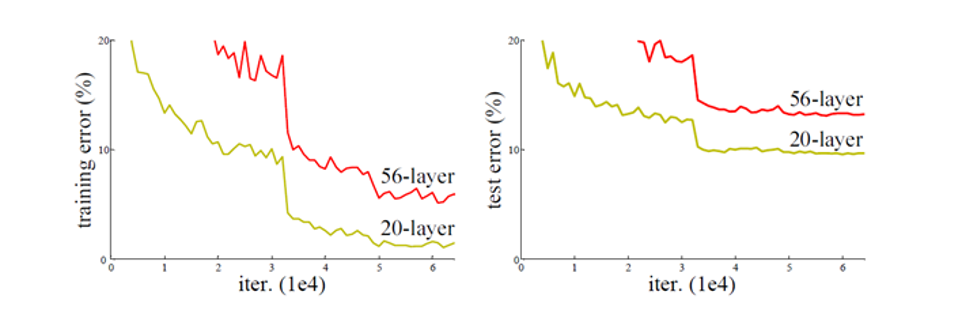
分析问题可能产生的原因:
这就很奇怪了。理论上,56层的网络至少可以这么学:前20层就学成那个20层网络的样子,后面36层就啥也不干(学成一个恒等映射 Identity Mapping),那它的性能至少也应该和20层的网络持平才对啊
是因为过拟合吗?
显然不可能,因为前20层的特征我50层的特征都有,而且我后面36层的啥都不干,按理说我们两个训练出来的错误值应该是一样的,但是很明显:

但事实是,让神经网络去学习一个“啥也不干”的恒等映射,竟然是一件非常困难的事!对于传统的网络结构,堆叠更多的层,反而损害了模型的性能。
所以,ResNet的核心目标就是:让超深的网络至少能不差于较浅的网络。换言之,解决网络退化问题。
三:公式+代码+理解:
1.例子
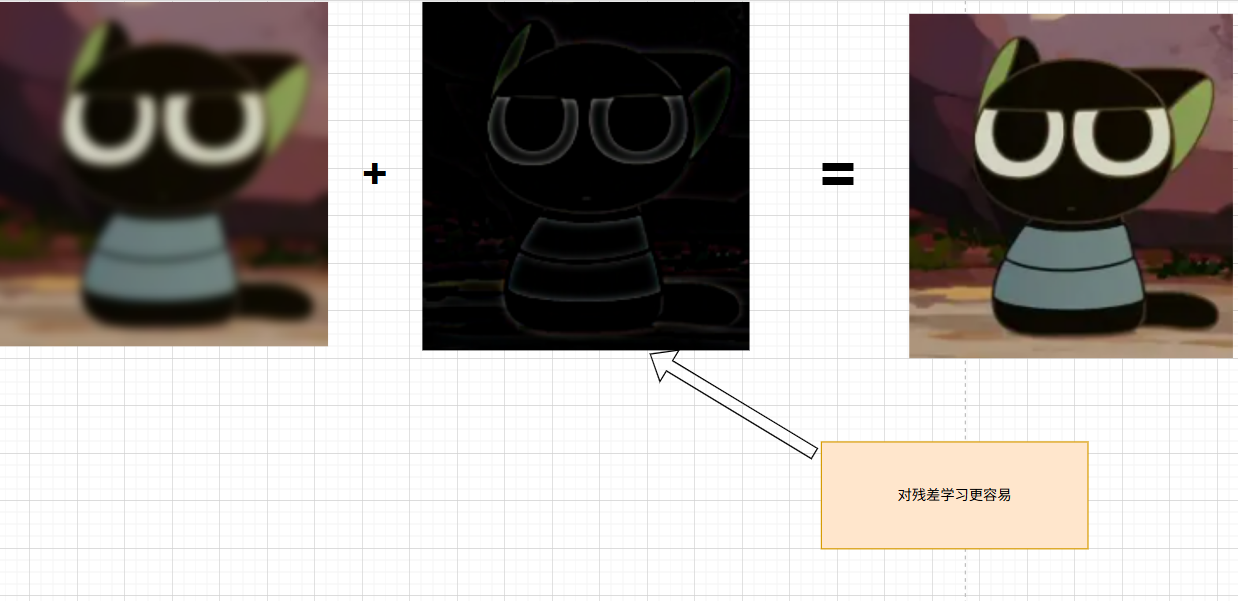
在进行公式的解释之前,我还是想直观的让大家理解一下:如下图所示


我们想要让训练模型通过训练,可以让我们左边的模糊的图来得到我们右边的清晰图
若不采用ResNet,而是基于我们此前设计的卷积神经网络进行训练,其整体框架结构大致如下
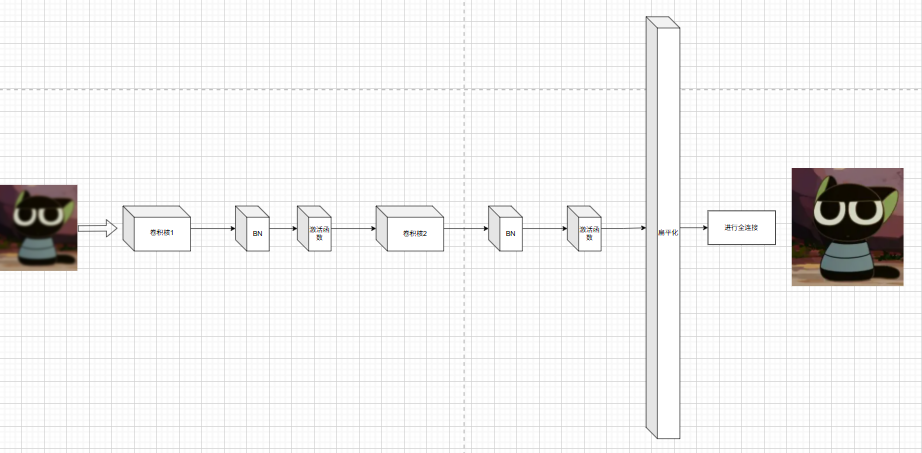
我们重点关注卷积运算:
我们通过两次卷积操作,每次卷积后都应用了批归一化(BN)和激活函数,从而提取了大量特征。虽然浅层网络可以很好地完成这些操作,但随着网络深度的增加,会出现网络退化问题。更深的网络结构可能导致先前提取的特征逐渐丢失。那么,如何在不引发网络退化的情况下,有效增加网络深度呢?
请看下图:

我我们用清晰图减去训练的模糊图得到差值结果,然后调整等式结构

这一等式为我们带来了重要启示:既然让深层网络直接学习恒等映射(即完整图像)非常困难,那么我们可以采用更高效的方式。具体而言,我们不再要求网络直接重构原始图像,而是让它学习图像与目标之间的变化量,也就是所谓的残差。
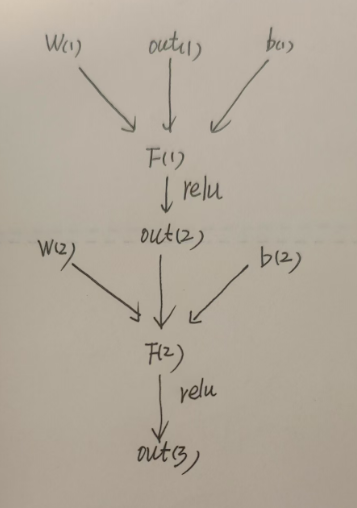
上图展示了我们之前的学习状态。具体来说,公式描述了两次卷积操作的过程:首先,通过卷积核的权重和偏置值与上一层的图像输出out(1)进行线性组合,得到F(1);接着,将F(1)输入Relu激活函数处理后得到out(2);最后,重复上述卷积操作得到下一层的输出out(3),但是我们分析了这种描述的网络,会随着卷积层数越来越深而出现网络退化的,那我们因该怎么办?
根据前文的分析,我们不直接学习模糊图像的全部特征,而是学习两张图像相减得到的残差。这种对残差的学习方式,相比直接学习原图会更加容易。
因此,我们的目标需要调整:每次训练网络时,只需专注于优化残差部分。那么,如何修改相应的公式呢?
2.公式
2.1传统CNN公式:
首先,之前的公式的表达式是这样子:(这里角标我就不抽象画了)

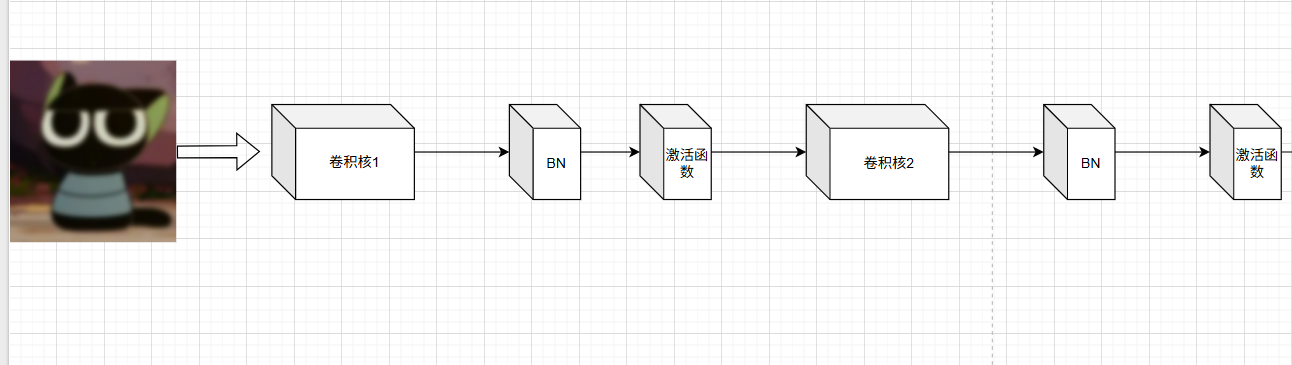
为了让各位读者更清晰,我再把我的之前画的图和这公式放在一起一下:


这两张图和上面的公式都描述的是没有引入resnet 残差的情况
2.2 resnst 公式
我们引入残差
首先残差的定义:
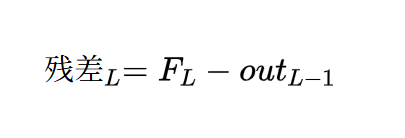
这里我为了方便计算:

则我们的公式就成型了:

所以:
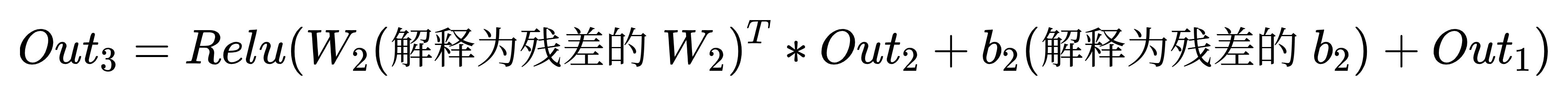
对比一下,我们之前写的式子:
| 传统卷积 | resnet |
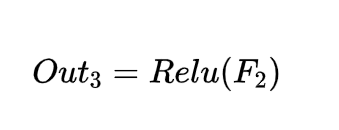 |
|
通过对比分析可以发现,这两个表达式实际上是恒等式。因为左边的F_2等价于右边的残差F_2(解释为残差)(即残差项)加上前一层输出out_1。
这意味着训练目标发生了改变:传统卷积训练的是整个线性表达式F_2的权重,这个权重描述的是完整图像特征;而在残差结构中,我们仅训练残差项F_2(解释为残差)(即残差部分)。虽然最终输出仍会将残差与前一层输出out_1相加(相当于完整的F_2(左边表格的F_2)表达式),但实际优化的是残差部分的权重参数。
如果还是不懂的话:

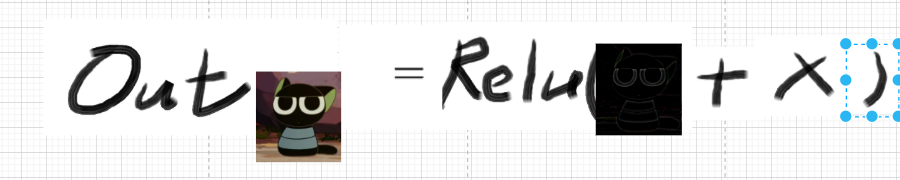
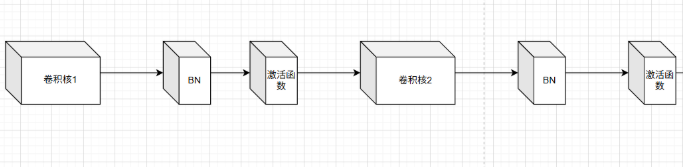
我绘制了一张示意图以便更清晰地说明。如第一张图所示,它训练的是整个模糊图像;而第二张图中,我们只需训练残差部分。将残差与前一层的输出相加后,再输入激活函数中进行下一层的训练。
所以说这就是我们resnet的网络的绝妙之处,我们逃避掉了对整张图的训练,而反过来只训练它的残差,这样子我们既不会迷失在深层网络中,又能加深网络的层数,因为我们始终有前者的输出,作为参考,我们的训练结果只可能比上一次更好,而不是比上一次更差!!!!!,是不是很牛逼
这种机制就像烹饪过程:每次进行下一步时,都会参考上一步的成果,只需专注于完善当前步骤(残差部分),而不是每次都从头开始或者盲目推进。这样的方式大大降低了失败的风险。
3.代码实现:
到这里,我们心中所有的疑虑应该都解除了,所以说我们下来看代码;
首先我们在没有resnet时网络时这样的

现在我们只需要:
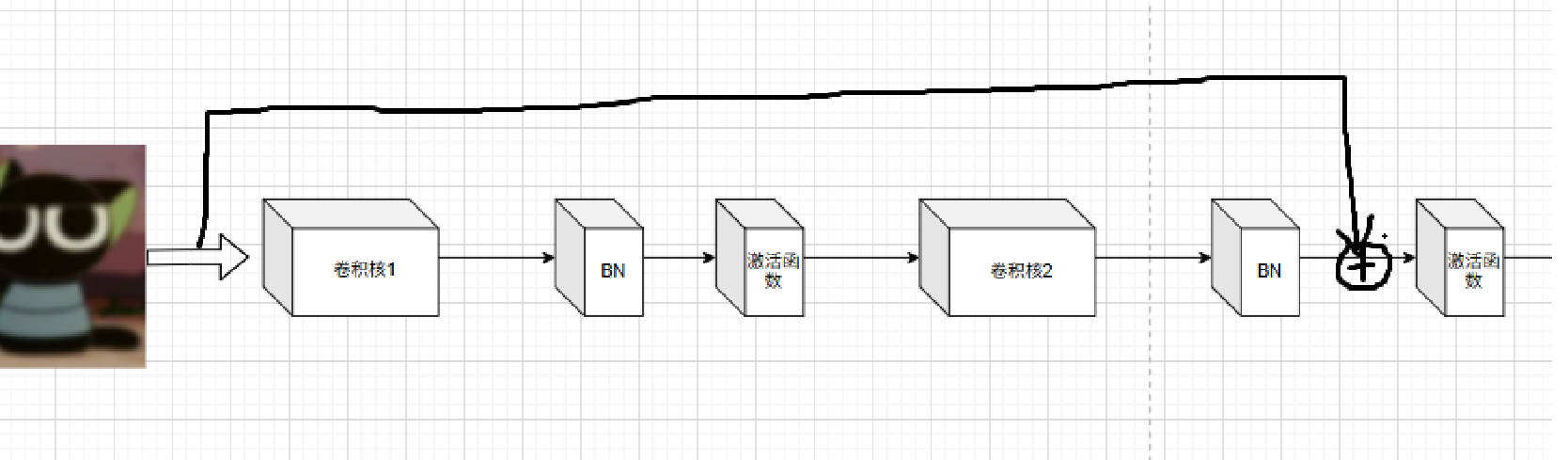
没错,我们只需要将我们开始的输入加到我们下一次卷积训练的激活函数之前进行相加,我们就瞬间改变了训练网络中训练的对象,我们就瞬间把残差作为了训练对象
而代码也特别简单:
如下图一,这是我们没有引入残差的代码,就是普通的卷积神经网络,它进行了两次卷积,然后最后由激活函数输出,这个代码和我们上面的卷积框架是一样的,这个代码它的训练目标,我们可以发现是图像的整体,所以训练的参数也描述的是图像的整体
def forward(self, x: Tensor) -> Tensor:
identity = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)而如下图二,我们引入了残差,我们只需要进行一个操作,就是把之前的输入作为第二次卷积激活函数之前的输出加进去,然后一起作为激活函数的变量进行输出,只需要这一步,代码就立刻改变了训练网络的训练对象,训练残差,所以说它的训练参数也从训练整个图像参数变成了只对残差进行训练的参数
def forward(self, x: Tensor) -> Tensor:
identity = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
if self.downsample is not None:
identity = self.downsample(x)
out += identity
out = self.relu(out)算法讲解到此结束。仅需在CNN基础上改一行代码,我们就能显著提升训练网络的性能,使网络层数得以加深,同时避免因层数增加导致的训练退化问题。而这么牛逼的算法提出者是:这位大佬:何恺明,他太刁了,大家可以搜一下,我当时学完resnet 的时候只能说:艺术品!!!
但是读到这里,可以给我一个免费的关注和赞吗
