数据结构
一、C++ STL
1. Sequence Containers:维持顺序的容器。
2. Container Adaptors:基于其它容器实现的数据结构。
3. Associative Containers:实现了排好序的数据结构。
4. Unordered Associative Containers:对每个 Associative Containers 实现了哈希版本。
二、经典问题
1. 数组
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
利用数组这种数据结构建立 n 个桶,把所有重复出现的位置进行标记,然后再遍历一遍数组,即可找到没有出现过的数字。进一步地,我们可以直接对原数组进行标记:把重复出现的数字在原数组出现的位置设为负数,最后仍然为正数的位置即为没有出现过的数。
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> ans;
for(const int & num: nums){
int pos = abs(num) - 1;
if(nums[pos] > 0){
nums[pos] = -nums[pos];
}
}
for(int i=0; i<nums.size(); ++i){
if(nums[i] > 0){
ans.push_back(i + 1);
}
}
return ans;
}
};给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
每次只考虑四个间隔 90 度的位置,可以进行 O ( 1 ) 额外空间的旋转。
对于矩阵中第 i 行的第 j 个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。由于矩阵中的行列从 0 开始计数,因此对于矩阵中的元素
,在旋转后,它的新位置为
。
方法一:根据旋转前后的位置关系进行原地旋转。
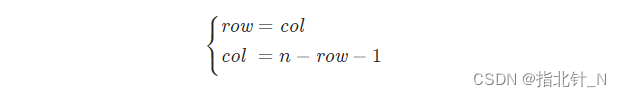
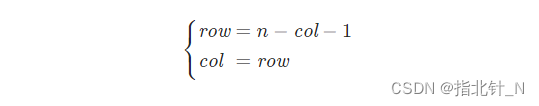
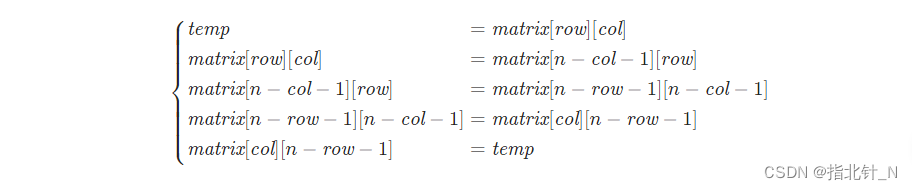
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int temp = 0, n = matrix.size() - 1;
for(int i=0; i<=n; ++i){
for(int j=i; j<n-i; ++j){
temp = matrix[j][n - i];
matrix[j][n - i] = matrix[i][j];
matrix[i][j] = matrix[n - j][i];
matrix[n - j][i] = matrix[n - i][n - j];
matrix[n - i][n - j] = temp;
}
}
}
};方法二:用翻转操作代替旋转操作。
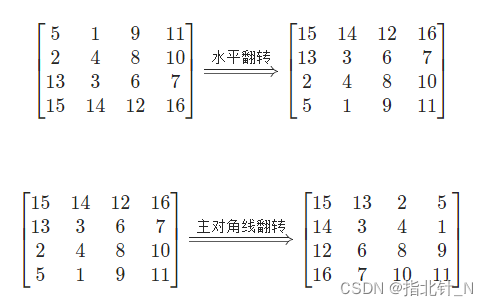

class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size() ;
// 水平翻转
for(int i=0; i<n/2; ++i){
for(int j=0; j<n; ++j){
swap(matrix[i][j], matrix[n - i - 1][j]);
}
}
// 主对角线翻转
for(int i=0; i<n; ++i){
for(int j=0; j<i; ++j){
swap(matrix[i][j], matrix[j][i]);
}
}
}
};
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
这道题有一个简单的技巧:我们可以从右上角开始查找,若当前值大于待搜索值,我们向左移动一位;若当前值小于待搜索值,我们向下移动一位。如果最终移动到左下角时仍不等于待搜索值,则说明待搜索值不存在于矩阵中。
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
if(m == 0) return false;
int i = 0, j = n - 1;
while(i < m && j >= 0){
if(matrix[i][j] == target){
return true;
}else if(matrix[i][j] > target){
--j;
}else{
++i;
}
}
return false;
}
};769. Max Chunks To Make Sorted
给定一个长度为 n 的整数数组 arr ,它表示在 [0, n - 1] 范围内的整数的排列。
我们将 arr 分割成若干 块 (即分区),并对每个块单独排序。将它们连接起来后,使得连接的结果和按升序排序后的原数组相同。
返回数组能分成的最多块数量。
从左往右遍历,同时记录当前的最大值,每当当前最大值等于数组位置时,我们可以多一次分割。为什么可以通过这个算法解决问题呢?如果当前最大值大于数组位置,则说明右边一定有小于数组位置的数字,需要把它也加入待排序的子数组;又因为数组只包含不重复的 0 到 n - 1 ,所以当前最大值一定不会小于数组位置。所以每当当前最大值等于数组位置时,假设为 p ,我们可以成功完成一次分割,并且其与上一次分割位置 q 之间的值一定是 q + 1 到 p 的所有数字。
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
int chunks = 0, cur_max = 0;
for(int i=0; i<arr.size(); ++i){
cur_max = max(cur_max, arr[i]);
if(cur_max == i){
++chunks;
}
}
return chunks;
}
};2. 栈和队列
232. Implement Queue using Stacks
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
我们可以用两个栈来实现一个队列:因为我们需要得到先入先出的结果,所以必定要通过一个额外栈翻转一次数组。这个翻转过程既可以在插入时完成,也可以在取值时完成。
class MyQueue {
stack<int> in, out;
public:
MyQueue() {
}
void push(int x) {
in.push(x);
}
int pop() {
in2out();
int x = out.top();
out.pop();
return x;
}
int peek() {
in2out();
return out.top();
}
void in2out(){
if(out.empty()){
while(!in.empty()){
int x = in.top();
in.pop();
out.push(x);
}
}
}
bool empty() {
return in.empty() && out.empty();
}
};
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue* obj = new MyQueue();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->peek();
* bool param_4 = obj->empty();
*/设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
我们可以额外建立一个新栈,栈顶表示原栈里所有值的最小值。每当在原栈里插入一个数字时,若该数字小于等于新栈栈顶,则表示这个数字在原栈里是最小值,我们将其同时插入新栈内。每当从原栈里取出一个数字时,若该数字等于新栈栈顶,则表示这个数是原栈里的最小值之一,我们同时取出新栈栈顶的值。一个写起来更简单但是时间复杂度略高的方法是,我们每次插入原栈时,都向新栈插入一次原栈里所有值的最小值(新栈栈顶和待插入值中小的那一个);每次从原栈里取出数字时,同样取出新栈的栈顶。这样可以避免判断,但是每次都要插入和取出。我们这里只展示第一种写法。
class MinStack {
stack<int> s, min_s;
public:
MinStack() {
}
void push(int val) {
s.push(val);
if(min_s.empty() || min_s.top() >= val){
min_s.push(val);
}
}
void pop() {
if(!min_s.empty() && min_s.top() == s.top()){
min_s.pop();
}
s.pop();
}
int top() {
return s.top();
}
int getMin() {
return min_s.top();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(val);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
括号匹配是典型的使用栈来解决的问题。我们从左往右遍历,每当遇到左括号便放入栈内,遇到右括号则判断其和栈顶的括号是否是统一类型,是则从栈内取出左括号,否则说明字符串不合法。
class Solution {
public:
bool isValid(string s) {
stack<int> parsed;
for(int i=0; i<s.length(); ++i){
if(s[i] == '(' || s[i] == '[' || s[i] == '{'){
parsed.push(s[i]);
}else{
if(parsed.empty()){
return false;
}
char c = parsed.top();
if((s[i] == ')' && c == '(') || (s[i] == ']' && c == '[') || (s[i] == '}' && c == '{')){
parsed.pop();
}else {
return false;
}
}
}
return parsed.empty();
}
};3. 单调栈
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
我们可以维持一个单调递减的栈,表示每天的温度;为了方便计算天数差,我们这里存放位置(即日期)而非温度本身。我们从左向右遍历温度数组,对于每个日期 p ,如果 p 的温度比栈顶存储位置 q 的温度高,则我们取出 q ,并记录 q 需要等待的天数为 p − q ;我们重复这一过程,直到 p 的温度小于等于栈顶存储位置的温度(或空栈)时,我们将 p 插入栈顶,然后考虑下一天。在这个过程中,栈内数组永远保持单调递减,避免了使用排序进行比较。最后若栈内剩余一些日期,则说明它们之后都没有出现更暖和的日期。
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
stack<int> indices;
int n = temperatures.size();
vector<int> ans(n);
for(int i=0; i<n; ++i){
while(!indices.empty()){
int pre_index = indices.top();
if(temperatures[i] <= temperatures[pre_index]){
break;
}
indices.pop();
ans[pre_index] = i - pre_index;
}
indices.push(i);
}
return ans;
}
};4. 优先队列
vector<int> heap;
// 上浮
void swim(int pos){
while(pos > 0 && heap[(pos - 1)/2] < heap[pos]){
swap(heap[(pos - 1)/2], heap[pos]);
pos = (pos - 1)/2;
}
}
// 下沉
void sink(int pos){
while(2 * pos + 1 <= N){
int i = 2 * pos + 1;
if(i < N && heap[i] < heap[i + 1]) ++i;
if(heap[pos] >= heap[i]) break;
swap(heap[pos], heap[i]);
pos = i;
}
}
// 插入任意值:把新的数字放在最后一位,然后上浮
void push(int x){
heap.push_back(x);
swim(heap.size() - 1);
}
// 删除最大值:把最后一个数字挪到开头,然后下沉
void pop(){
heap[0] = heap.back();
heap.pop_back();
sink(0);
}
// 获得最大值
int top(){
return heap[0];
}
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
本题可以有很多中解法,比如类似于归并排序进行两两合并。我们这里展示一个速度比较快的方法,即把所有的链表存储在一个优先队列中, 每次提取所有链表头部节点值最小的那个节点,直到所有链表都被提取完为止。注意因为 Comp 函数默认是对最大堆进行比较并维持递增关系,如果我们想要获取最小的节点值,则我们需要实现一个最小堆,因此比较函数应该维持递减关系,所以 operator() 中返回时用大于号而不是等增关系时的小于号进行比较。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
// 自定义优先队列的元素比较方法 Compa
struct Comp{
bool operator() (ListNode* l1, ListNode* l2){
return l1->val > l2->val;
}
};
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
if(lists.empty()) return nullptr;
priority_queue<ListNode*, vector<ListNode*>, Comp> q;
for(ListNode* list: lists){
if(list){
q.push(list);
}
}
ListNode* dummy = new ListNode(0), *cur = dummy;
while(!q.empty()){
// 取出最小的节点插入新链表
cur->next = q.top();
q.pop();
cur = cur->next;
// 再将这个节点的后继节点放入队列中
if(cur->next){
q.push(cur->next);
}
}
return dummy->next;
}
};城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度,请返回 由这些建筑物形成的 天际线 。
每个建筑物的几何信息由数组 buildings 表示,其中三元组 buildings[i] = [lefti, righti, heighti] 表示:
lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。
你可以假设所有的建筑都是完美的长方形,在高度为 0 的绝对平坦的表面上。
天际线 应该表示为由 “关键点” 组成的列表,格式 [[x1,y1],[x2,y2],...] ,并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点,y 坐标始终为 0 ,仅用于标记天际线的终点。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
注意:输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[...[2 3], [4 5], [12 7], ...]
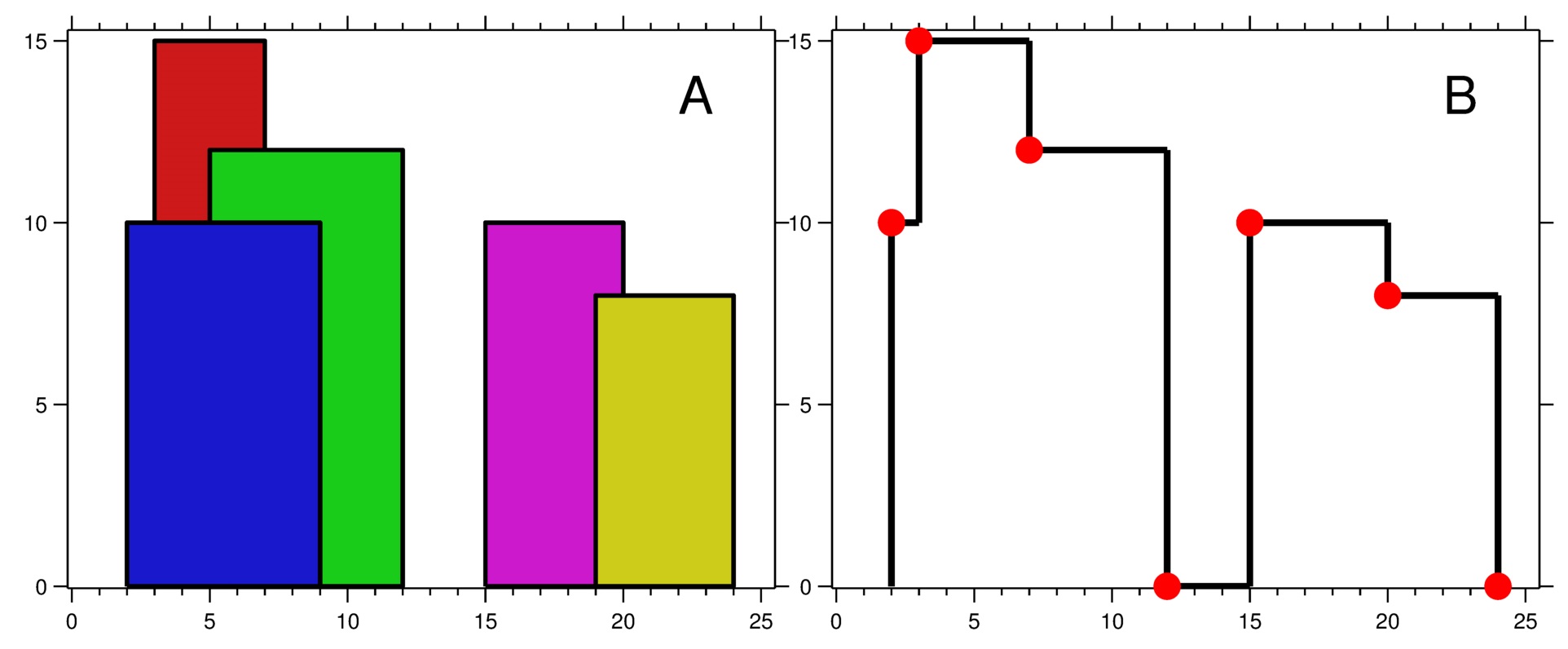
我们可以使用优先队列储存每个建筑物的高度和右端(这里使用 pair,其默认比较函数是先比较第一个值,如果相等则再比较第二个值),从而获取目前会拔高天际线、且妨碍到前一个建筑物(的右端端点)的下一个建筑物。
如果是「从下到上」转向「水平方向」,纵坐标最大的点是关键点,不pop();
如果是「从上到下」转向「水平方向」,纵坐标第二大的点是关键点,pop()。
class Solution {
public:
vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
vector<vector<int>> ans;
priority_queue<pair<int, int>> max_heap; // <高度, 右端>
int i = 0, len = buildings.size();
int cur_x, cur_h;
// 保证建筑没遍历完,或者遍历完了但是max_heap没遍历完
while(i < len || !max_heap.empty()){
// 如果当前建筑左坐标比优先队列最高建筑的右坐标小,判断上升转折点
if(max_heap.empty() || i < len && buildings[i][0] <= max_heap.top().second){
cur_x = buildings[i][0];
// 所有左端相同的建筑放入优先队列
while(i < len && cur_x == buildings[i][0]){
max_heap.emplace(buildings[i][2], buildings[i][1]);\
++i;
}
}else{
// 如果当前建筑左坐标比优先队列的最大高度建筑的右坐标大,说明一群建筑结束,可以开始判断该群建筑的所有下降转折点了
cur_x = max_heap.top().second;
// 把所有优先队列内比头右坐标小的剔除(下降点只会在最高点的右边)
while(!max_heap.empty() && cur_x >= max_heap.top().second){
max_heap.pop();
}
}
cur_h = (max_heap.empty())? 0: max_heap.top().first;
// 因为只有判断下降时才会pop优先队列,所以在同一群建筑中和优先队列最高高度不一样才加入输出
if(ans.empty() || cur_h != ans.back()[1]){
ans.push_back({cur_x, cur_h});
}
}
return ans;
}
};5. 双端队列
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
我们可以利用双端队列(单调队列)进行操作:每当向右移动时,把窗口左端的值从队列左端剔除,把队列右边小于窗口右端的值全部剔除。这样双端队列的最左端永远是当前窗口内的最大值。另外,这道题也是单调栈的一种延申:该双端队列利用从左到右递减来维持大小关系。
双端队列的作用是保证每次L边界右移时从队列头弹出的都是当前窗口的最大值,队列中存储元素下标即可。
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
deque<int> dq;
vector<int> ans;
for(int i=0; i<nums.size(); ++i){
// 如果首元素超过滑动窗口,弹出
if(!dq.empty() && dq.front() == i - k){
dq.pop_front();
}
// 构造单调递减队列
while(!dq.empty() && nums[i] > nums[dq.back()]){
dq.pop_back();
}
dq.push_back(i);
// 在滑动窗口内每次都要添加最大值
if(i >= k - 1){
ans.push_back(nums[dq.front()]);
}
}
return ans;
}
};6. 哈希表
哈希表,又称散列表,使用 O(n) 空间复杂度存储数据,通过哈希函数映射位置,从而实现近似 O(1) 时间复杂度的插入、查找、删除等操作。 C++ 中的哈希集合为 unordered_set,可以查找元素是否在集合中。如果需要同时存储键和值,则需要用 unordered_map,可以用来统计频率,记录内容等等。如果元素有穷,并且范围不大,那么可以用一个固定大小的数组来存储或统计元素。例如我们需要统计一个字符串中所有字母的出现次数,则可以用一个长度为 26 的数组来进行统计,其哈希函数即为字母在字母表的位置,这样空间复杂度就可以降低为常数。
一个简单的哈希表的实现如下。
// 一个简单的对整数实现的哈希函数
int MyHash(const int& key, const int& tableSize){
return key % tableSize;
}
template <typename T>;
class HashTable{
public:
// size最好是质数
HashTable(int size = 31){
hash_table_.reverse(size);
hash_table_.reverse(size);
}
~HashTable();
// 查找哈希表是否存在该值
bool Contains(const T& obj){
const list<T>& slot = hash_table_[Hash(obj)];
auto it = slot.cbegin();
for(;it != slot.cend() && *it != obj; ++it);
return it != slot.cend();
}
// 插入值
bool Insert(const T& obj){
if(Contains(obj)){
return false;
}
hash_table_[Hash(obj)].push_front(obj);
return true;
}
// 删除值
bool Remove(const T& obj){
list<T>& slot = hash_table_[Hash(obj)];
auto it = find(slot.begin(), slot.end(), obj);
if(it == slot.end()){
return false;
}
slot.erase(it);
return true;
}
private:
vector<list<T>> hash_table_;
// 哈希函数
int Hash(const T& obj) const{
return MyHash(obj, hash_table_.size());
}
}如果需要大小关系的维持,且插入查找并不过于频繁,则可以使用有序的 set/map 来代替 unordered_set/unordered_map。
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
// 键是数字,值是该数字在数组的位置
unordered_map<int, int> hash;
vector<int> ans;
for(int i=0; i<nums.size(); ++i){
int num = nums[i];
auto pos = hash.find(target - num);
if(pos == hash.end()){
hash[num] = i;
}else{
ans.push_back(pos->second);
ans.push_back(i);
break;
}
}
return ans;
}
};128. Longest Consecutive Sequence
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
我们可以把所有数字放到一个哈希表,然后不断地从哈希表中任意取一个值,并删除掉其之前之后的所有连续数字,然后更新目前的最长连续序列长度。重复这一过程,我们就可以找到所有的连续数字序列。
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
unordered_set<int> hash;
for(const int& num: nums){
hash.insert(num);
}
int ans = 0;
while(!hash.empty()){
int cur = *(hash.begin());
hash.erase(cur);
int next = cur + 1, pre = cur - 1;
while(hash.count(next)){
hash.erase(next++);
}
while(hash.count(pre)){
hash.erase(pre--);
}
ans = max(ans, next - pre - 1);
}
return ans;
}
}; 给你一个数组 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
对于每个点,我们对其它点建立哈希表,统计同一斜率的点一共有多少个。这里利用的原理 是,一条线可以由一个点和斜率而唯一确定。另外也要考虑斜率不存在和重复坐标的情况。 本题也利用了一个小技巧:在遍历每个点时,对于数组中位置 i 的点,我们只需要考虑 i 之 后的点即可,因为 i 之前的点已经考虑过 i 了。
class Solution {
public:
int maxPoints(vector<vector<int>>& points) {
unordered_map<double, int> hash;
int max_count = 0, same_y = 1, same = 1;
for(int i=0; i<points.size(); ++i){
same_y = 1, same = 1;
for(int j=i+1; j<points.size(); ++j){
if(points[i][1] == points[j][1]){
++same_y;
if(points[i][0] == points[j][0]){
++same;
}
}else{
double dx = points[i][0] - points[j][0];
double dy = points[i][1] - points[j][1];
++hash[dx/dy];
}
}
max_count = max(max_count, same_y);
for(auto item: hash){
max_count = max(max_count, same + item.second);
}
hash.clear();
}
return max_count;
}
};7. 多重集合和映射
给你一份航线列表 tickets ,其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。
例如,行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前。
假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。
本题可以先用哈希表记录起止机场,其中键是起始机场,值是一个多重集合,表示对应的终止机场。因为一个人可能坐过重复的线路,所以我们需要使用多重集合储存重复值。储存完成之后,我们可以利用栈来恢复从终点到起点飞行的顺序,再将结果逆序得到从起点到终点的顺序。
class Solution {
public:
vector<string> findItinerary(vector<vector<string>>& tickets) {
vector<string> ans;
if(tickets.empty()){
return ans;
}
unordered_map<string, multiset<string>> hash;
for(const auto& ticket: tickets){
hash[ticket[0]].insert(ticket[1]);
}
stack<string> s;
s.push("JFK");
while(!s.empty()){
string next = s.top();
if(hash[next].empty()){
ans.push_back(next);
s.pop();
}else{
s.push(*hash[next].begin());
hash[next].erase(hash[next].begin());
}
}
reverse(ans.begin(), ans.end());
return ans;
}
};8. 前缀和与积分图
一维的前缀和,二维的积分图,都是把每个位置之前的一维线段或二维矩形预先存储,方便 加速计算。如果需要对前缀和或积分图的值做寻址,则要存在哈希表里;如果要对每个位置记录 前缀和或积分图的值,则可以储存到一维或二维数组里,也常常伴随着动态规划。
303. Range Sum Query - Immutable
给定一个整数数组 nums,处理以下类型的多个查询:
计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left <= right
实现 NumArray 类:
NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ,包含 left 和 right 两点(也就是 nums[left] + nums[left + 1] + ... + nums[right] )
class NumArray {
vector<int> psum;
public:
NumArray(vector<int>& nums): psum(nums.size() + 1, 0){
partial_sum(nums.begin(), nums.end(), psum.begin() + 1);
}
int sumRange(int left, int right) {
return psum[right + 1] - psum[left];
}
};
/**
* Your NumArray object will be instantiated and called as such:
* NumArray* obj = new NumArray(nums);
* int param_1 = obj->sumRange(left,right);
*/304. Range Sum Query 2D - Immutable
给定一个二维矩阵 matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为(row2, col2) 。
实现 NumMatrix 类:
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化 int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和 。
类似于前缀和,我们可以把这种思想拓展到二维,即积分图(image integral)。我们可以先建 立一个 intergral 矩阵,intergral[i][j] 表示以位置 (0, 0) 为左上角、位置 (i-1, j-1) 为右下角的长方形 中所有数字的和。 如图 1 所示,我们可以用动态规划来计算 integral 矩阵:intergral[i][j] = matrix[i-1][j-1] + integral[i-1][j] + integral[i][j-1] - integral[i-1][j-1],即当前坐标的数字 + 上面长方形的数字和 + 左 边长方形的数字和 - 上面长方形和左边长方形重合面积(即左上一格的长方形)中的数字和。
如图 2 所示,假设我们要查询长方形 E 的数字和,因为 E = D − B − C + A,我们发现 E 其 实可以由四个位置的积分图结果进行加减运算得到。因此这个算法在预处理时的时间复杂度为 O(mn),而在查询时的时间复杂度仅为 O(1)。
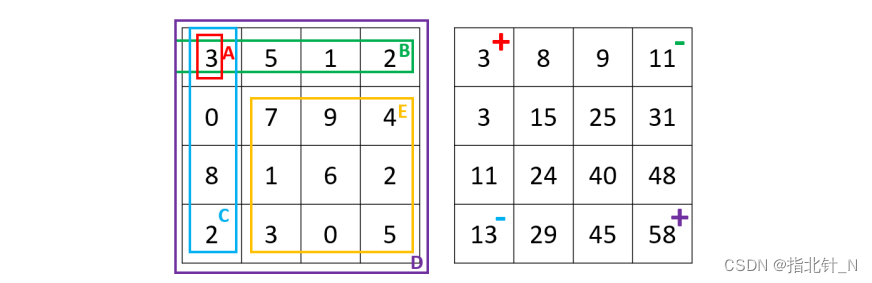
class NumMatrix {
vector<vector<int>> integral;
public:
NumMatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = m > 0? matrix[0].size(): 0;
integral = vector<vector<int>>(m + 1, vector<int>(n + 1, 0));
for(int i=1; i<=m; ++i){
for(int j=1; j<=n; ++j){
integral[i][j] = matrix[i - 1][j - 1] + integral[i - 1][j] + integral[i][j - 1] - integral[i - 1][j - 1];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
return integral[row2 + 1][col2 + 1] - integral[row1][col2 + 1] - integral[row2 + 1][col1] + integral[row1][col1];
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix* obj = new NumMatrix(matrix);
* int param_1 = obj->sumRegion(row1,col1,row2,col2);
*/ 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。
本题同样是利用前缀和,不同的是这里我们使用一个哈希表 hashmap,其键是前缀和,而值是 该前缀和出现的次数。在我们遍历到位置 i 时,假设当前的前缀和是 psum,那么 hashmap[psum-k] 即为以当前位置结尾、满足条件的区间个数。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int count = 0, psum = 0;
unordered_map<int, int> hashmap;
hashmap[0] = 1; // 初始化很重要
for(int i: nums){
psum += i;
count += hashmap[psum - k];
++hashmap[psum];
}
return count;
}
};三、巩固练习
欢迎大家共同学习和纠正指教