💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
💥1 概述
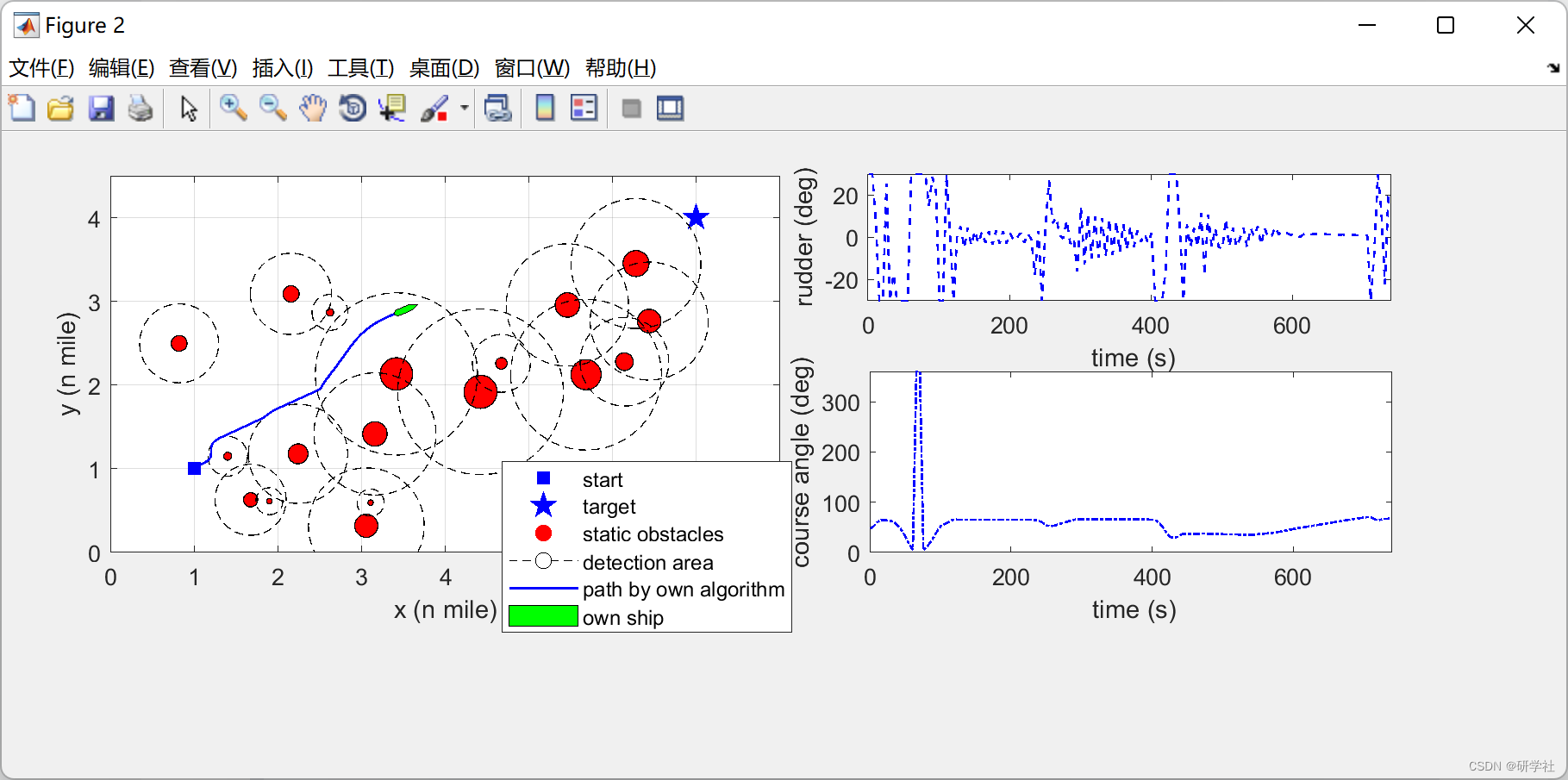
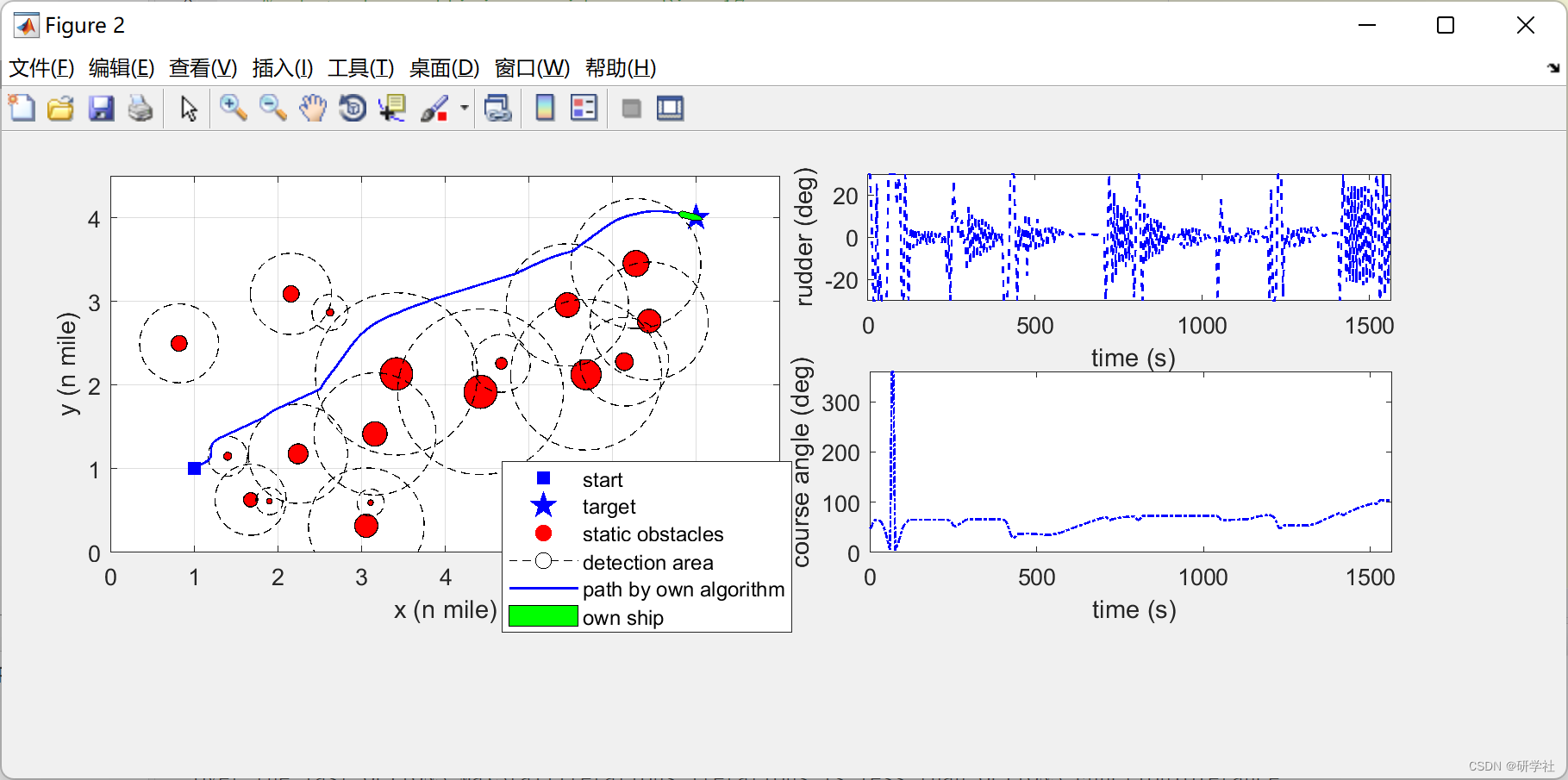
船舶运动规划是海上自主水面舰艇(MASS)自主导航的核心问题。该文提出一种考虑避碰规则的复杂遭遇场景模型预测人工势场(MPAPF)运动规划方法。建立了一个新的船舶域,其中设计了一个闭区间势场函数来表示船舶域的不可侵犯属性。在运动规划过程中,采用具有预定义速度的Nomoto模型来生成符合船舶运动学的可遵循路径。为解决传统人工势场(APF)方法的局部最优问题,保证复杂遭遇场景下的防撞安全,提出一种基于模型预测策略和人工势场的运动规划方法MPAPF。该方法将船舶运动规划问题转化为具有机动性、导航规则、通航航道等多重约束的非线性优化问题。4个算例的仿真结果表明,与APF、A星和快速探索随机树(RRT)的变体相比,所提出的MPAPF算法能够解决上述问题,并生成可行的运动路径,避免复杂遭遇场景下的船舶碰撞。
文献来源:

📚2 运行结果
输入预测步长(我们建议应该是1~10,在这个程序中,1步可能花费你120秒,而10步可能比1步高100倍。


部分代码:
%% initialization
static_obs_num = [12;6];
mailme = 0;
% static_obs_area = [0.8, 2, 7, 8;
% 2, 0.2, 10, 2];
static_obs_area = [0.5, 0, 4.5, 4;
4.5, 2, 6.5 3.5];
dynamic_ships = [1;1;1;1];
parameter.waterspeed = 0/1852;
parameter.waterangle = 45;
parameter.water = [sind(parameter.waterangle) cosd(parameter.waterangle)]*parameter.waterspeed;
parameter.minpotential = 0.001;
parameter.minpotential4ship = 0.01;
parameter.minobstacle = 0.03;
parameter.maxobstacle = 0.2;
parameter.safeobstacle = 5;
parameter.amplification = 5;
parameter.safecv = 2.5;%n mile safety collision aviodance distance
parameter.dangercv = 0.5;% danger collision aviodance distance
parameter.shipdomain = 5;
parameter.tsNum = 1;
%% simulation environment
map_size = [8,4.5];
start_point = [1 1];
end_point = [7,4];
tmp_end_point = end_point;
parameter.endbeta = -log(parameter.minpotential)/(norm(end_point-start_point)*2)^2;
mat_point = init_obstacles(static_obs_num,static_obs_area); % Generate static obstacles randomly
ship.speed = 8.23; % meters per second equal to 16 knots
ship.v = 0;
ship.data = [... data = [ U K T n3]
6 0.08 20 0.4
9 0.18 27 0.6
12 0.23 21 0.3 ];
% interpolate to find K and T as a function of U from MSS toolbox 'frigate'
prompt = 'Prediction Step\n'; % input the prediction step, 1~10
parameter.prediction_step = input(prompt);
ship.k = interp1(ship.data(:,1),ship.data(:,2),ship.speed,'linear','extrap'); %ship dynamic model you can change the dynamic model in shipdynamic.m
ship.T = interp1(ship.data(:,1),ship.data(:,3),ship.speed,'linear','extrap');
ship.n3 = interp1(ship.data(:,1),ship.data(:,4),ship.speed,'linear','extrap');
ship.Ddelta = 10*pi/180; % max rudder rate (rad/s)
ship.delta = 30*pi/180; % max rudder angle (rad)
ship.length = 100;
ship.p_leader = -8;
ship.alpha_leader = 3;
ship.yaw = 45;
ship.yaw_rate = 0;
ship.rudder = 0;
ship.rudder_rate = 0;
ship.position = [1 1];
ship.gamma = 1;
ship.lamda = log(1/parameter.minpotential4ship-1)/((parameter.shipdomain)^2-1);
ship.prediction_postion = [];
tsPath{parameter.tsNum} = [];
ship1 = ship;
parameter.scale = 1852; % 1852m in real world ,1 in simulation;
parameter.time = 5; % time per step
parameter.searching_step = 3000; % max searching step
parameter.map_size = map_size; % map size for display
parameter.map_min = 0.05; % minmum map details
parameter.end1 = 0.05;
% parameter.situs1 = [6.1 1.75 3.25 1.75];
parameter.situs1 = [6.1 3.9 3.25 1.75]; % a quaternion ship domain proposed in Wang 2010,situs1 means in head-on situation
parameter.situs2 = [6.1 3.9 3.25 1.75]; % a quaternion ship domain proposed in Wang 2010,situs2 means in crossing and give-way situation
parameter.situs3 = [0.0 0.0 0.00 0.00]; % a quaternion ship domain proposed in Wang 2010,situs3 means in crossing and stand-on situation
parameter.situs0 = [6.0 6.0 1.75 1.75]; % a quaternion ship domain proposed in Wang 2010,situs0 means in norm naviation situation
ship_scale = 1;
leader_stop = 0;
tic
draw2();
set(gcf,'position',[200 200 1361/1.5 750/2]);
hold on
LB_follower = [];
UB_follower = [];
for i = 1 : parameter.prediction_step
LB_follower = [LB_follower 0 -ship.delta];% lower limiting value
UB_follower = [UB_follower 0 ship.delta];% upper limiting value
end
parameter.navars = 2*parameter.prediction_step;% number of navars
targetship=init_ship(ship,'others',1000);
🎉3 参考文献
[1]He, Zhibo, et al. “A Novel Model Predictive Artificial Potential Field Based Ship Motion Planning Method Considering COLREGs for Complex Encounter Scenarios.” ISA Transactions, Elsevier BV, Sept. 2022, doi:10.1016/j.isatra.2022.09.007.