第一部分 --- 基本概念和排序方法概述
1.无序变有序的过程就称为排序
2.当参与排序的数据结点具有多个数据域的时候,我们的排序往往是真对某个数据域而言的
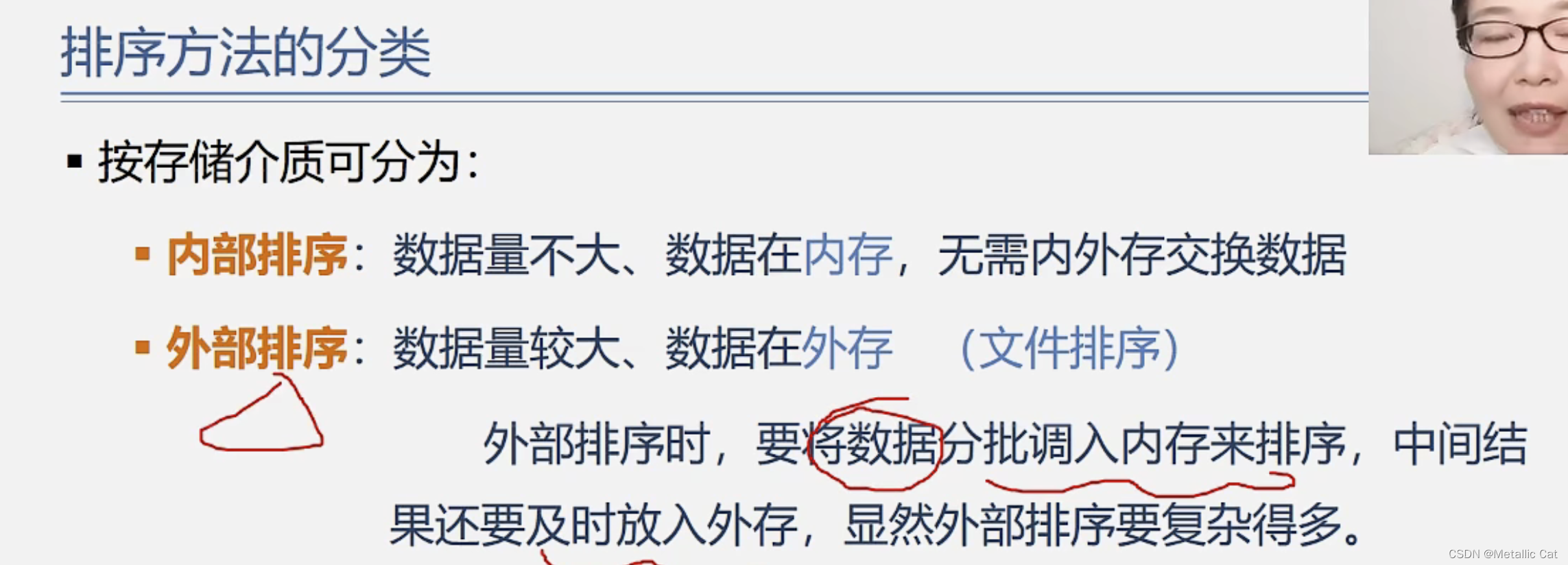
1.当要排序的数据量比较小的时候,我们可以直接在内存中实现排序,这就是内部排序
2.但是当数据量较大的时候(内存一次性装不下),我们需要先将数据存储到外存(文件等等)中,然后内存从外存中读取部分数据并进行排序,排好后再写入到外存中,然后再调用没被排序的数据进行排序,直到所有数据都排好序为止,这种就叫做外部排序

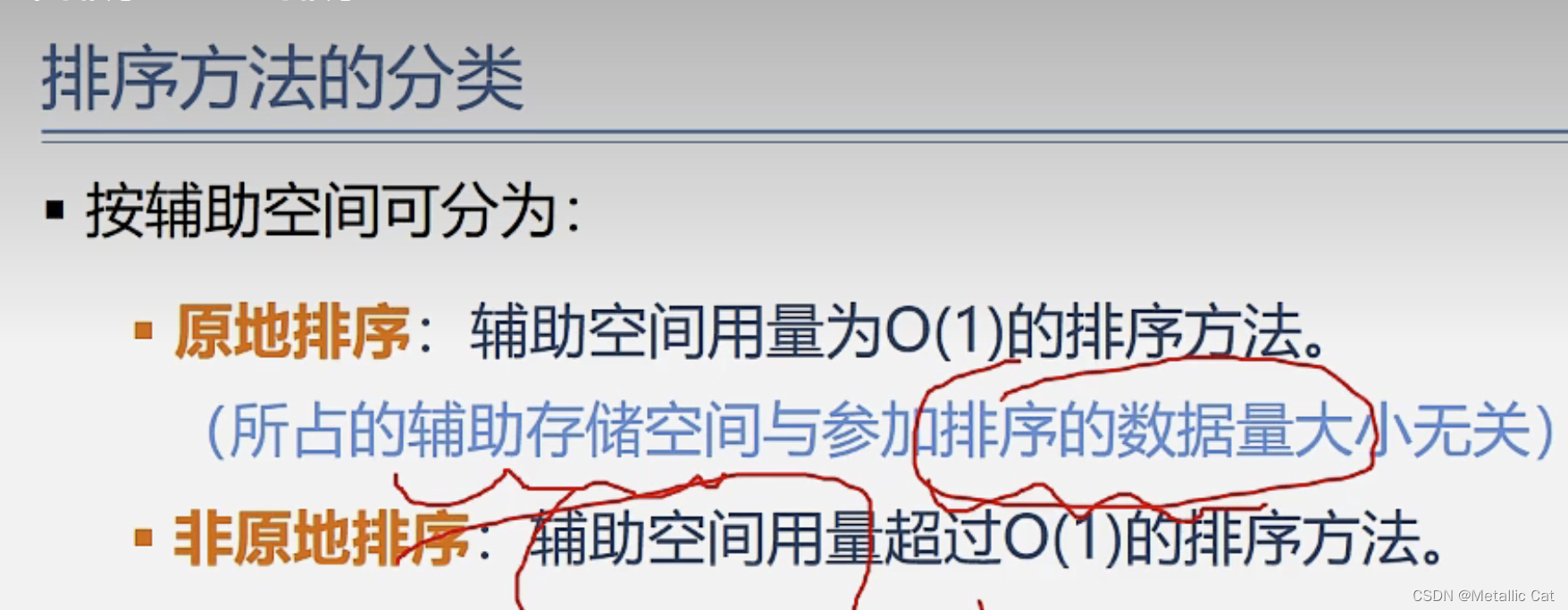
1.排序时只使用了一个空间(辅助控件用量为O(1)),称为原地排序
2.排序时使用了多个控件(辅助空间用来大于O(1)),称为非原地排序
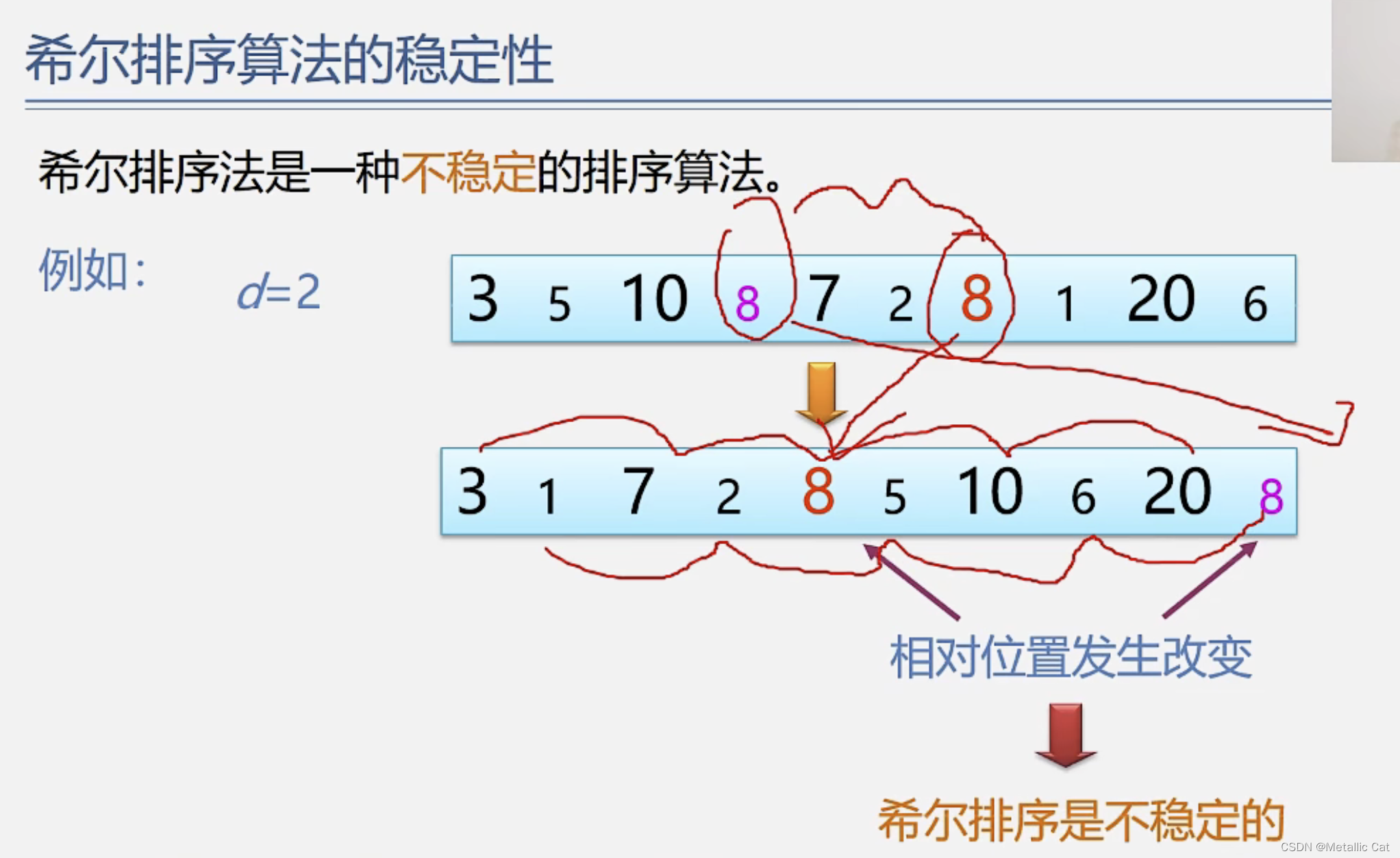
1.排序后相同元素之间的相对次序不发生改变就是稳定排序,反之就是不稳定排序(比如排序前有两个相同的元素A和B,其中A元素在B元素的前面,在进行排序后,如果A仍然在B的前面的话,则这个排序就是稳定排序)
1.示例1是稳定排序,示例2是非稳定排序

1.输入的数据越有序,排序的速度越慢,这就是非自然排序

1.第一步:进行各种宏定义
2.第二步:创建顺序表中要存储的数据元素(结构元素)对应的结构体类型,分别由一个整型还有其它数据域组成
3.第三步:创建顺序表类型,分别由存储具有第二步创建的结构体类型的元素的数组以及表示数组长度的整型。(其中数组的大小为我们要存储的元素 + 1,我们留一个下标为0的位置用作哨兵或者是缓冲区,从下标为1的位置开始存储元素)
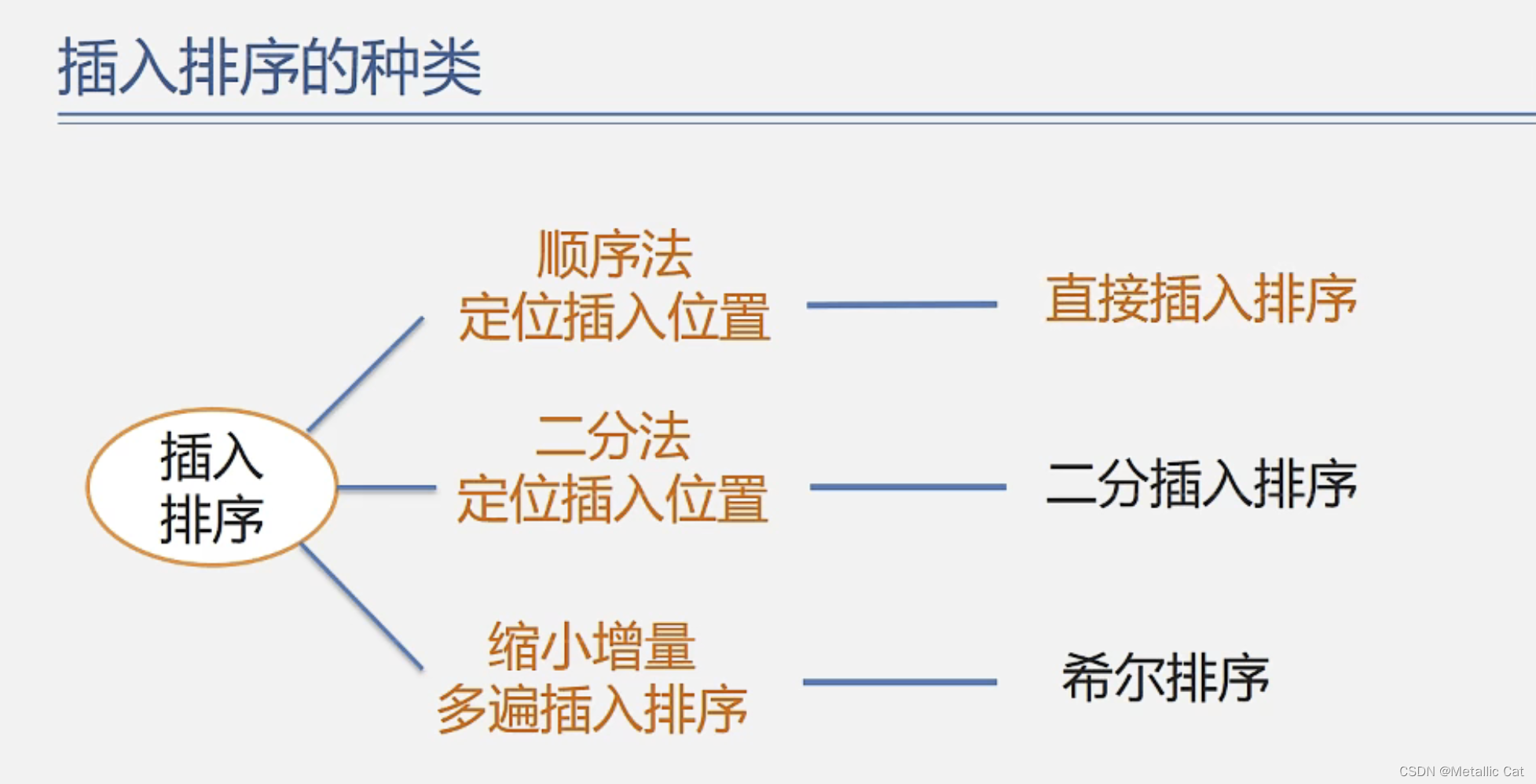
第二部分 --- 插入排序 之 直接插入排序
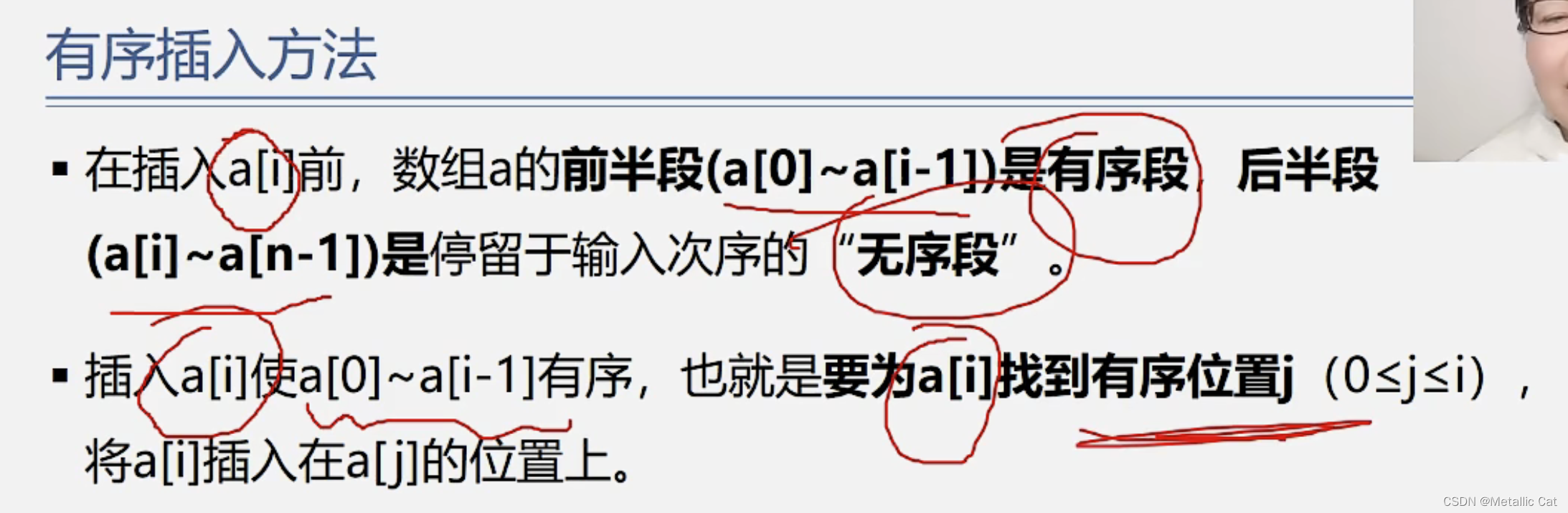
要执行插入操作的元素的后半段中都是还没有进行插入排序的元素,所以后半段是无序的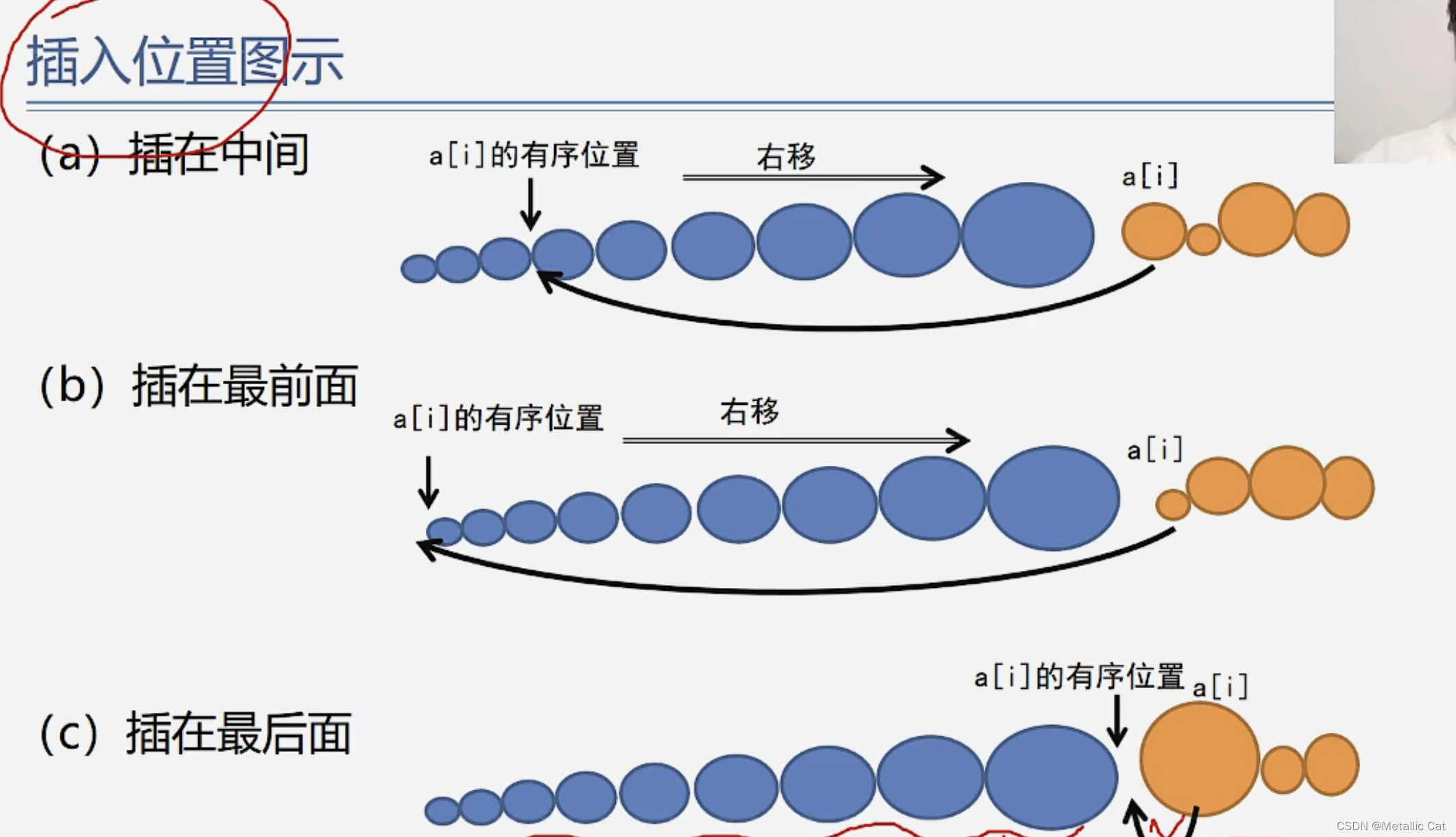
现在关键问题来了,我们如何获取某个元素的插入位置呢?

1.(在哨兵位置存放一份我们要插入的元素的拷贝,用这份拷贝来进行比较,并且当循环执行到这里的时候就会因为出现相等而自动停止循环,不需要我们加是否越界判断)
1.注意这里的直接插入排序的序列是由小到大排序,通过直接插入法按照顺序依次插入元素时,如果要插入的第i个元素比第i -1个元素大的话,第i个元素就不用变了(由小到大排,第i-1个元素就是前面有序序列的最大元素,要插入的元素比最大元素都大的话,那要插入的元素就是新的最大元素,位置不变)
2.如果比第 i -1个元素小的话,我们就需要从后往前依次比较,寻找可以插入的位置,当比较到哨兵时就会自动停止比较,此时要插入的元素就是比有序序列中的最小元素小(由小到排),则插入位置就是下标为1的位置,也就是哨兵的下标0 +1
3.寻找插入位置的过程中,每循环比较一次都需要将被比较的元素执行一次后移操作,为我们要插入的元素提供空间进行插入,并且保证有序序列依然有序

直接插入排序算法的平均比较次数和移动次数如下:
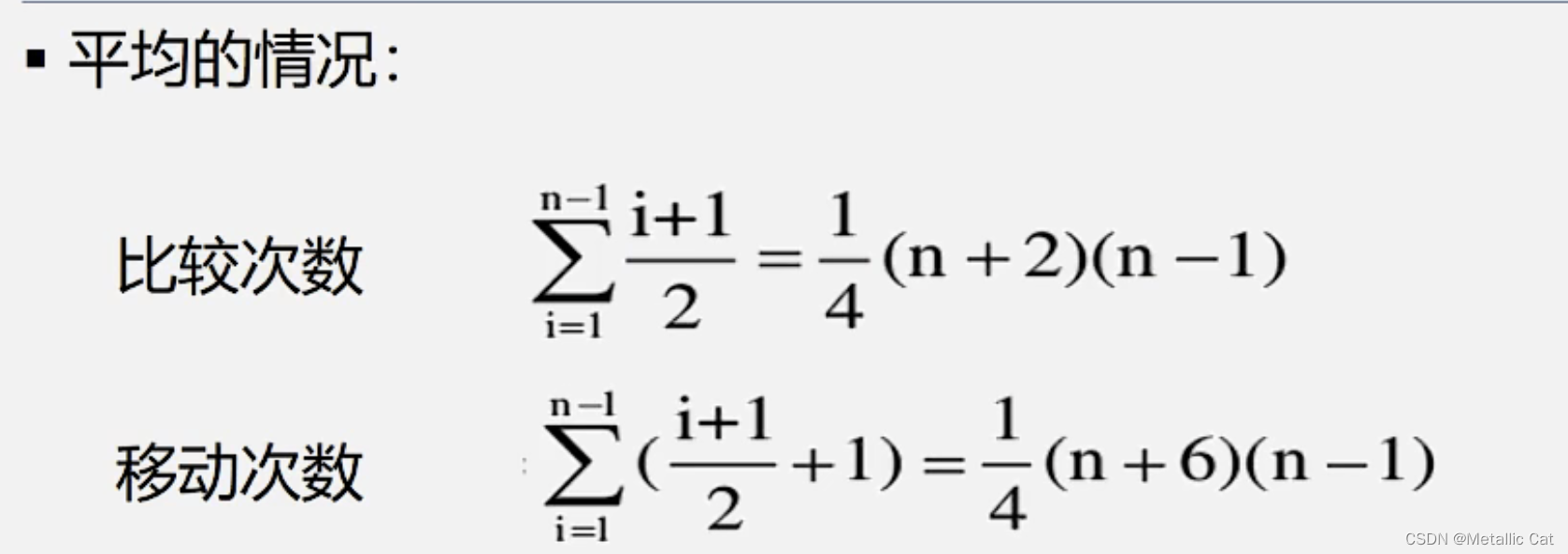

第三部分 --- 插入排序之折半插入排序

1.由于我们的元素要插入的部分是一个已经排好序的有序段,所以我们可以通过下面这几步来获得元素的插入位置
2.首先由于是顺序表存储的有序段,所以我们可以在这个表中使用二分查找,所以我们在这个有序段中使用二分查找方法去查找我们要插入的元素
3.由于有序段中一定没有我们要插入的元素(因为我们还没插入啊!),所以最终二分查找会在low > high(且low和high之间只差一) 的时候停止查找,此时我们的元素的插入位置就在下标为low和下标为high的元素之间,插入的步骤是:
4.由于是low大于high,所以我们要将下标为low的元素及其后面的元素都后移一位,然后将我们要插入的元素存放到空出来的下标为low的位置,这样我们就插入成功了
high + 1 对应的位置其实就是二分查找结束时low的位置(结束时low比high大,且low和high之间只差1)

1.对于直接插入排序而言,如果说待排序序列本身就已经是有序的话(由小到大排),那么我们每插入一个元素都只需要比较一次,假设有n个元素,总比较次数为n - 1次
但是当待排序序列为逆序的时候(由大到小排),总比较次数就变为 1 + 2 + 3 + ... + n - 1次
2.而对于折半插入排序而言,插入任意一个元素的比较次数不会受到待排序序列的初始排列的影响,而只与元素本身所处的位置有关
3.所以当待排序序列为无序/ 逆序的时候,折半插入排序的算法时间复杂度更低;当待排序序列为有序的时候,直接插入排序的算法时间复杂度更低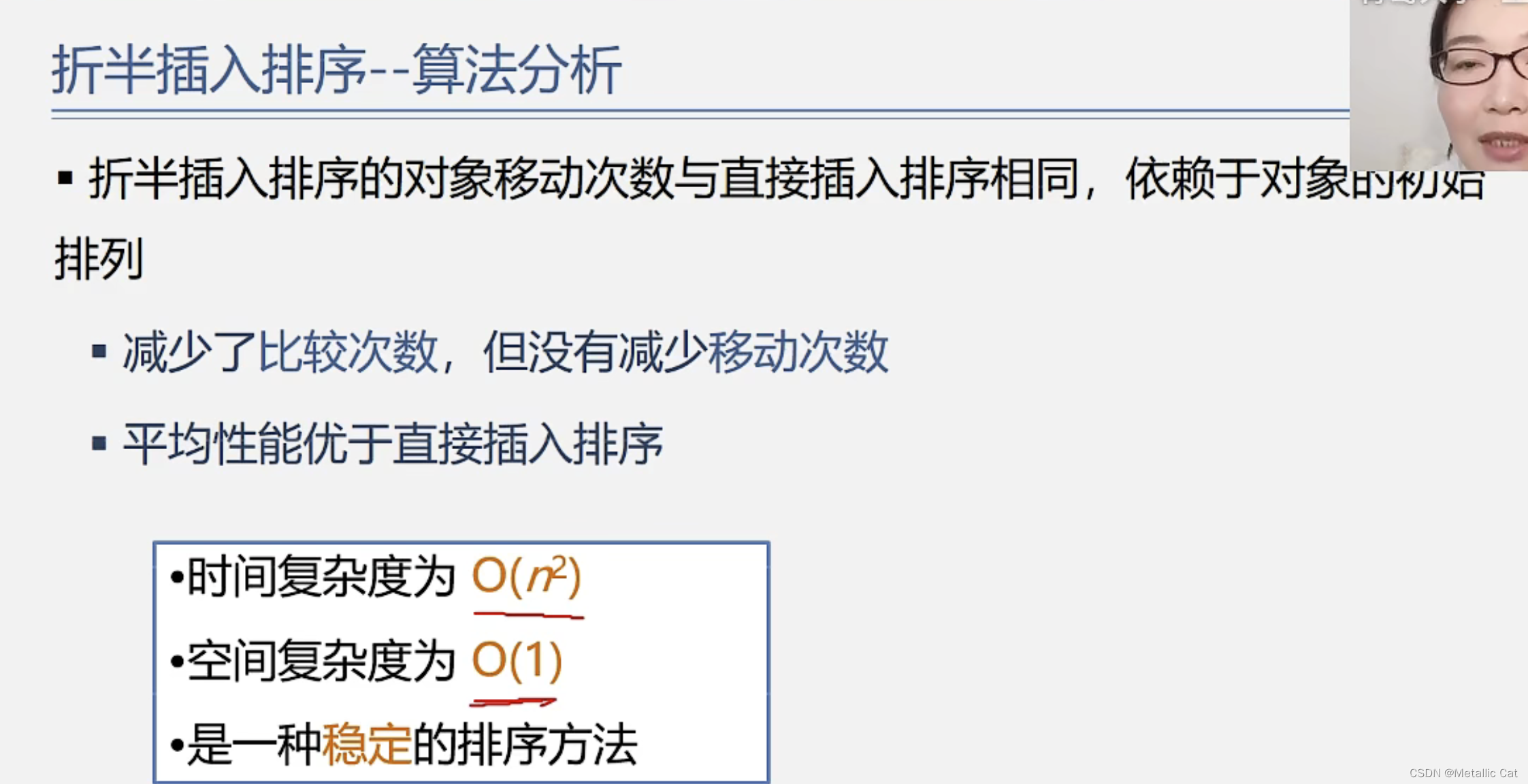
第四部分 --- 直接插入排序之希尔排序
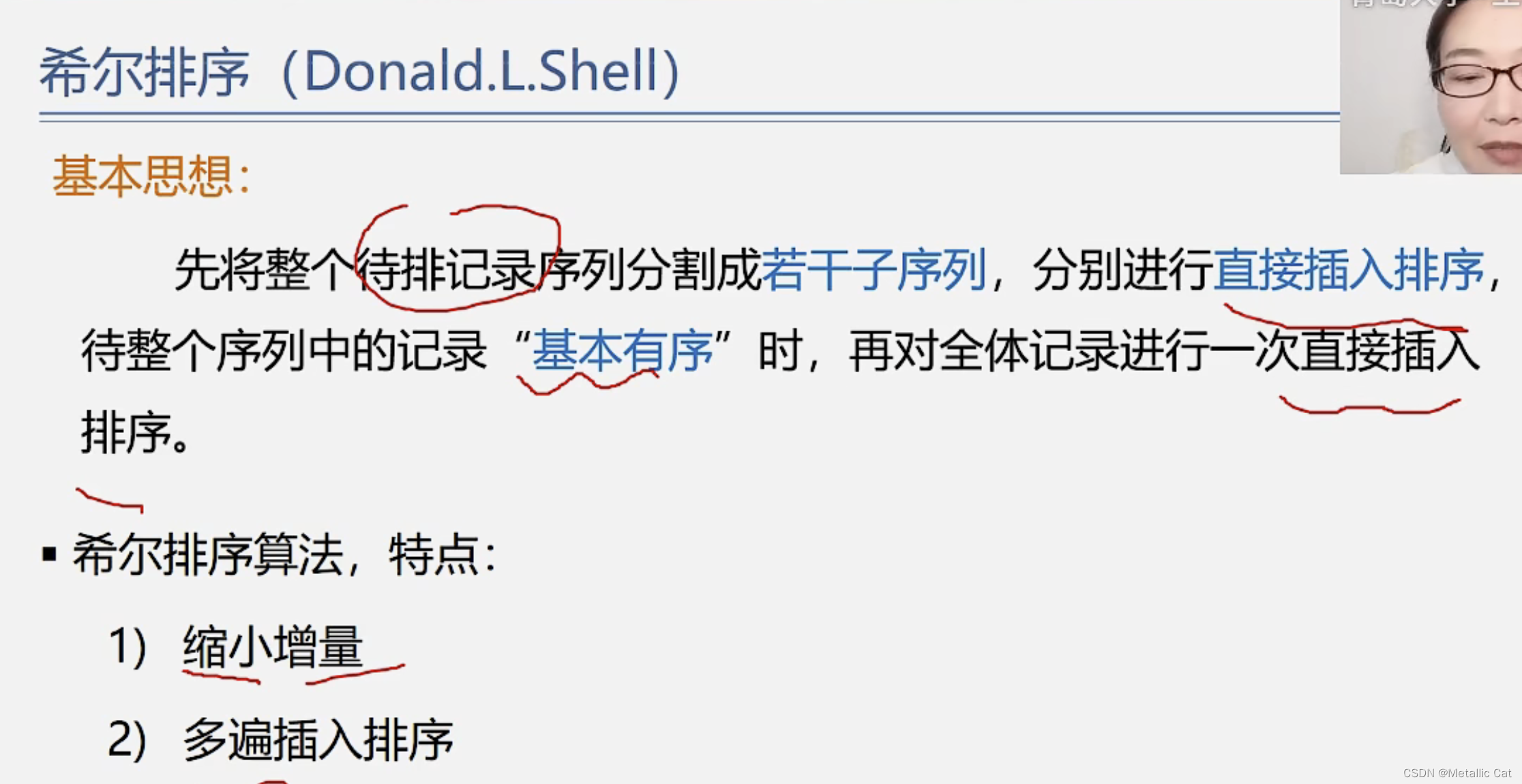

1.进行希尔排序的时候先设置一个增量,通过这个增量来选择元素,并对这些元素进行直接插入排序来交换它们的位置
2.所有元素都被选择一次之后再缩小增量(设置一个更小的增量),然后再将所有元素选择一次来进行排序
3.不停的缩小增量,当量增量为1的排序进行完毕后,希尔排序进行完毕,此时待排序序列也已经排好序了
4.通过设置增量来匹配元素进行排序可以实现两个目标:
一.增大元素移动的步伐,使得元素更快的接近自己在有序序列中的对应位置
二.每进行一次增量排序都能够使得序列的基本有序程度增大,降低下一次增量排序时的时间复杂度,不停的增量排序下去(增量递减),到最后我们就能够很好的降低增量为1(对所有元素进行直接插入排序)时的时间复杂度
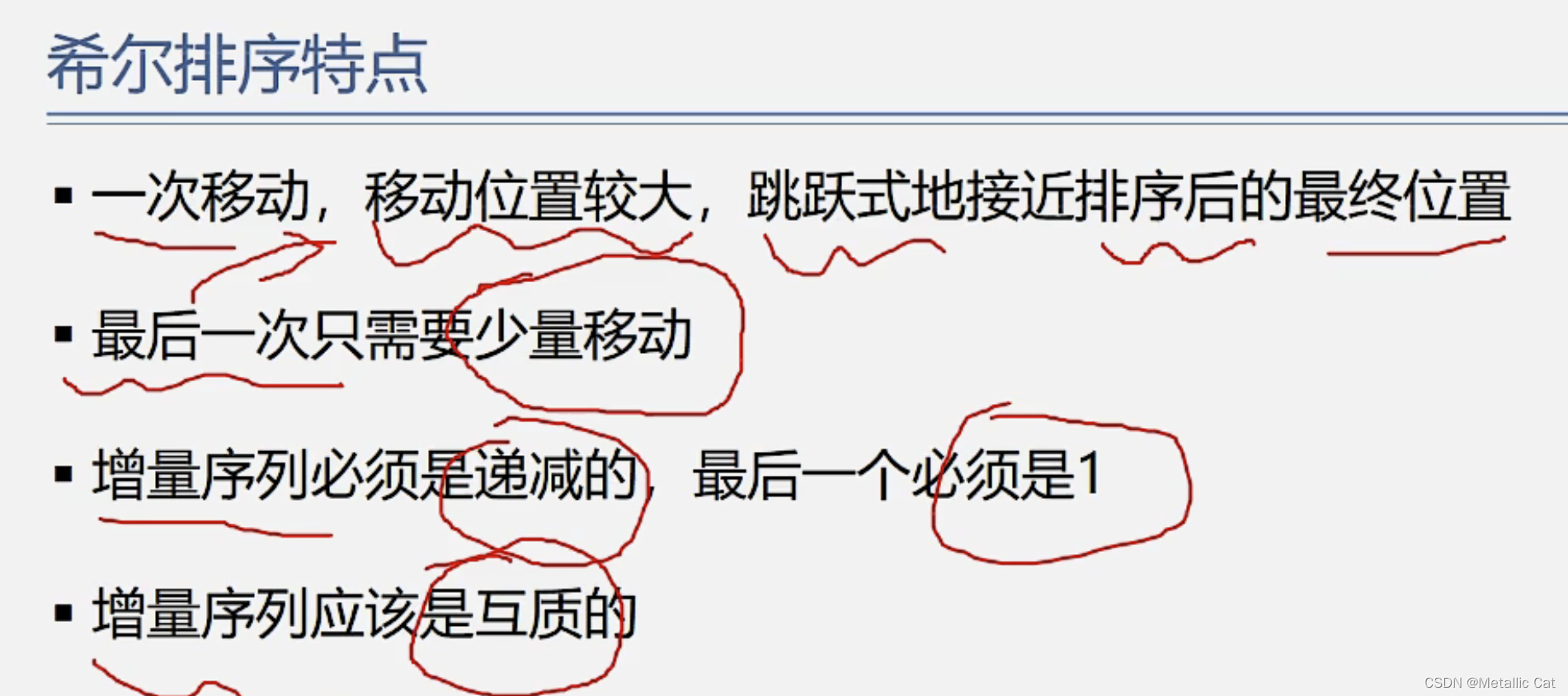
1.增量序列中的增量要求为质数(只能够被1和其本身整除的非负整数)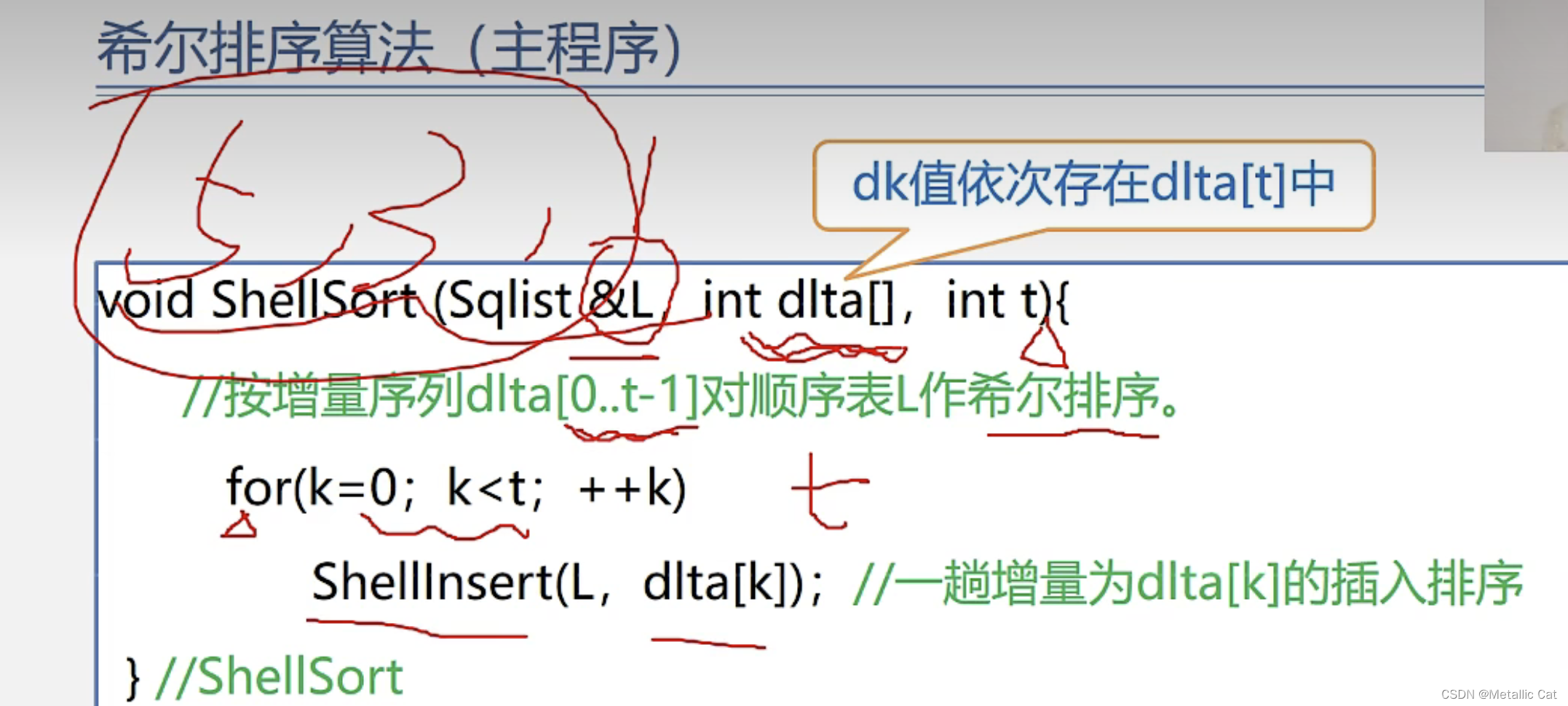
1.增量序列中有多少个增量我们就要进行多少次增量排序,这是第一层
2.每一次增量排序都要对应着执行一次插入排序,这是第二层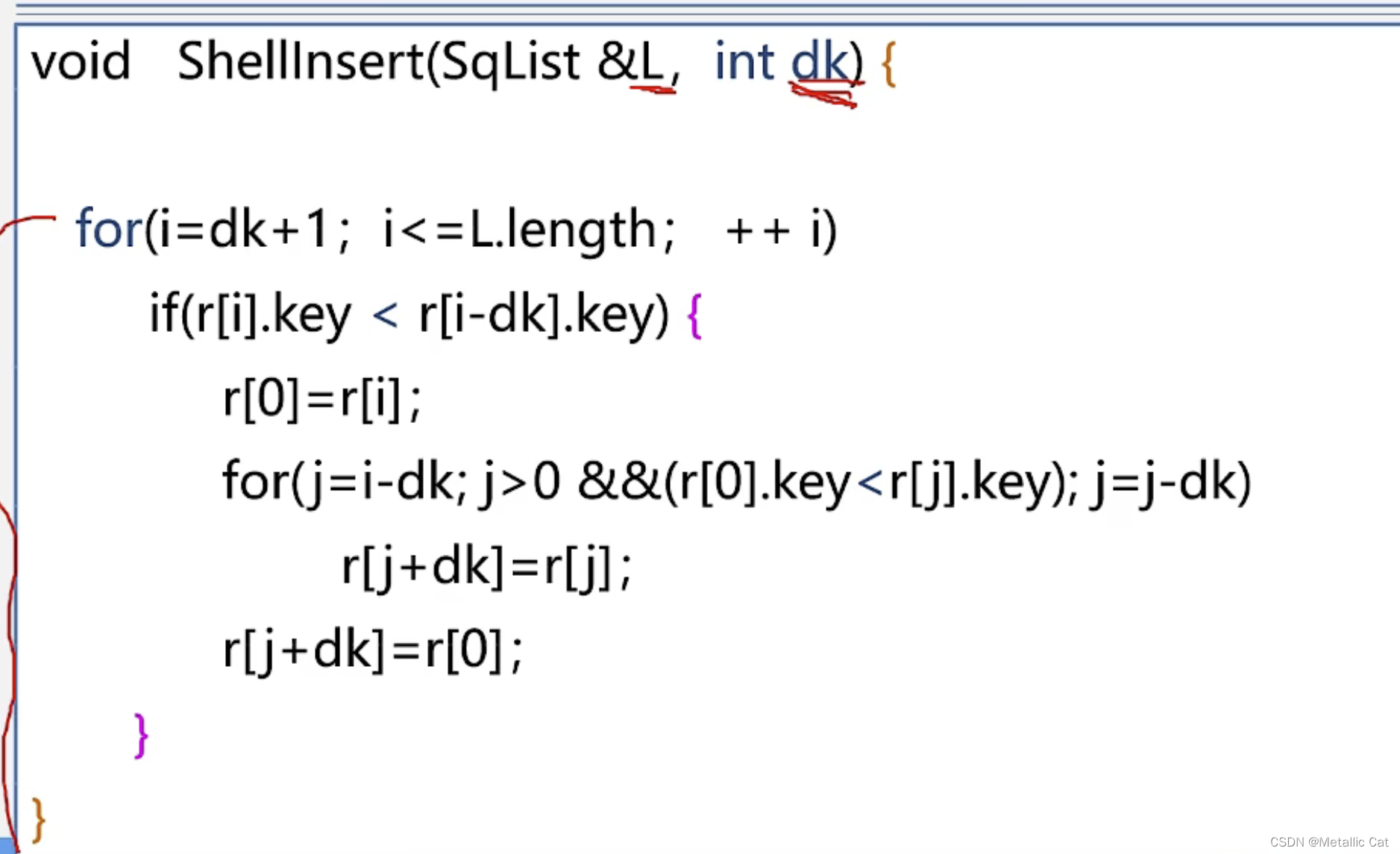
用上面这个循环是能够将所有元素都用增量进行匹配并排好序的
假设在增量K下,序列表中的元素可以匹配出 m 个子序列表,那我先进行第一次循环,将m个子序列表中第二个元素通过直接插入排序的方法插入到第一个元素构成的有序表中,所有子序列表都插入完毕后,再将m个子序列表中的第二个元素进行直接插入排序....就这样直到序列表中所有的元素都排好后循环结束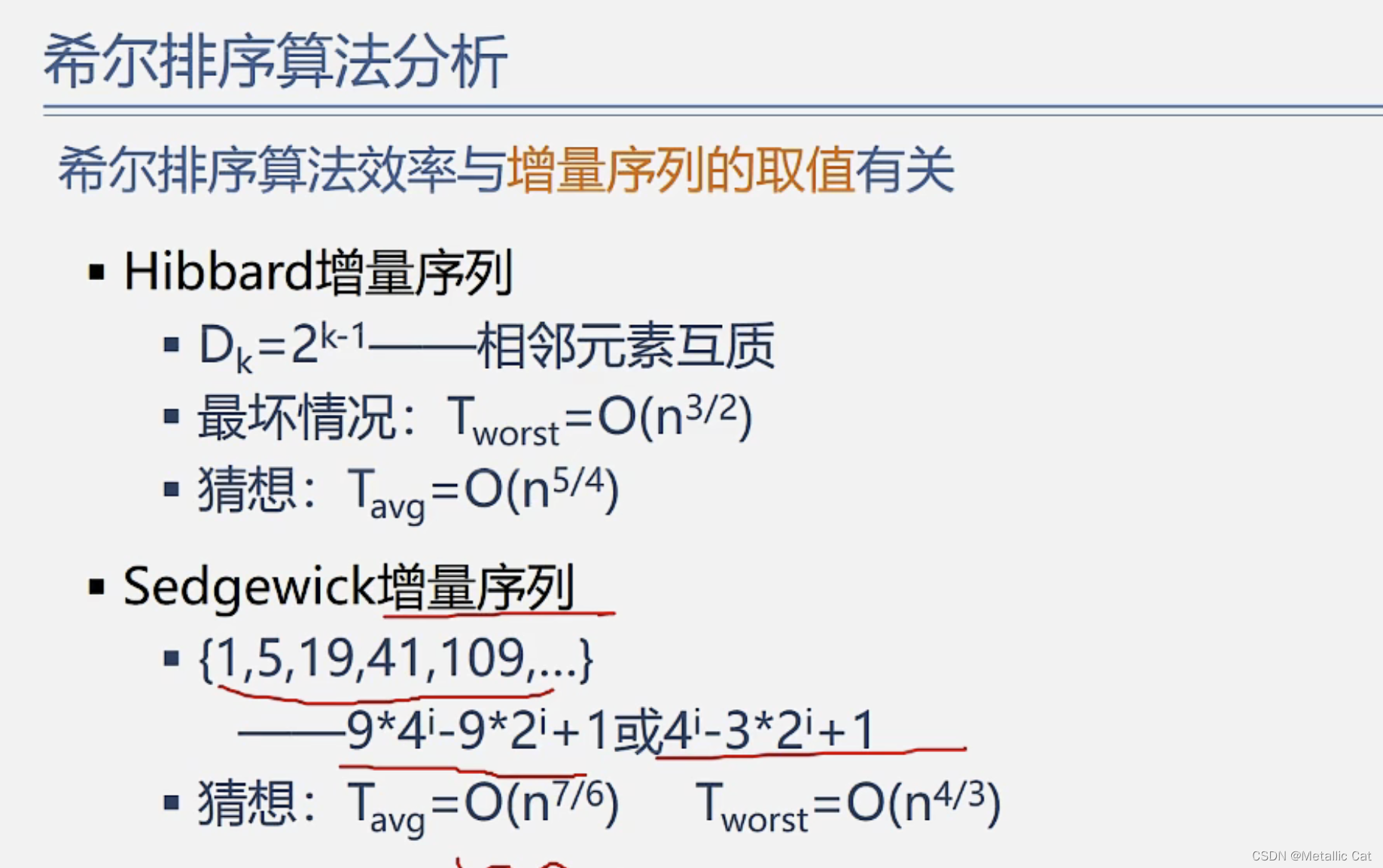
1.上面那个Hibbard增量序列应该是求出2的K次方后将结果减1,而不是2的(K - 1)次方

1.n是我们要排序的的元素个数,空间复杂度为O(1)是因为我们用了一个序列表中的一个空间作为辅助空间存放哨兵
2.增量序列中,最后一个增量必须为1,其它的增量则必须为质数