上一篇制造业综述中有提到该文章有提到从时间角度在线和离线故障诊断类型考虑因果关系,且用的是Granger因果。虽然文献有些老,感觉可能对自己有所启发,故特意找来看看。
Alizadeh E, El Koujok M, Ragab A, et al. A data-driven causality analysis tool for fault diagnosis in industrial processes[J]. IFAC-PapersOnLine, 2018, 51(24): 147-152.
知识点:
1. 过程的平稳性是在调查因果关系分析之前需要解决的一个重要部分。本文考虑了两种常见的平稳性,即趋势平稳性和差异平稳性。
(1)趋势平稳性:=常数+确定的平均趋势+均值问0的平稳状态
![]()
一般通过KPSS检验得到,就是假设H0平稳,如果拒绝H0那就是不平稳。
差异平稳DSP:D个不同趋势的时间,D=1时,可表示为![]() ,即△y=随机游走+极小值,故D=1,则y(t+1)=y(t)=c。
,即△y=随机游走+极小值,故D=1,则y(t+1)=y(t)=c。
(2)协整检验:Granger引入协整,考虑x(t)与 y(t)之间存在一阶差分平稳性。(一阶差分就是用于消除序列中随机游走的趋势,我们对时间序列进行一阶/多阶差分便可变为平稳性数据,然后我们就可用一些估计检验的方法了,这就是差分的意义。)
那么我们协整后对于Granger因果意味着啥?
如果x(t)与y(t)协整,那么我们认为它存在Granger因果关系,当然方向不确定。此外 ,反之,不满足。
Engle-Granger检验和Johansen检验被广泛用于确定随机过程是否协整。
2.Granger因果
设p阶VAR
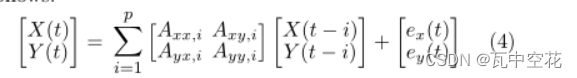
A为回归系数矩阵,e为残差。
可简化为: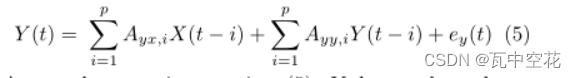
忽视X对Y的影响,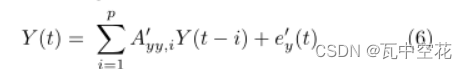 。
。
那么我们计算X对Y的Granger因果效应时可得:
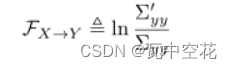 ,
,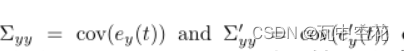
针对两个变量,上述还是好用的。但对X,Y,Z就不好用了。所以产生了conditional GC(2014) and partial GC (2008)。
3. 实验
实验一:
假设现有因果关系如图所示: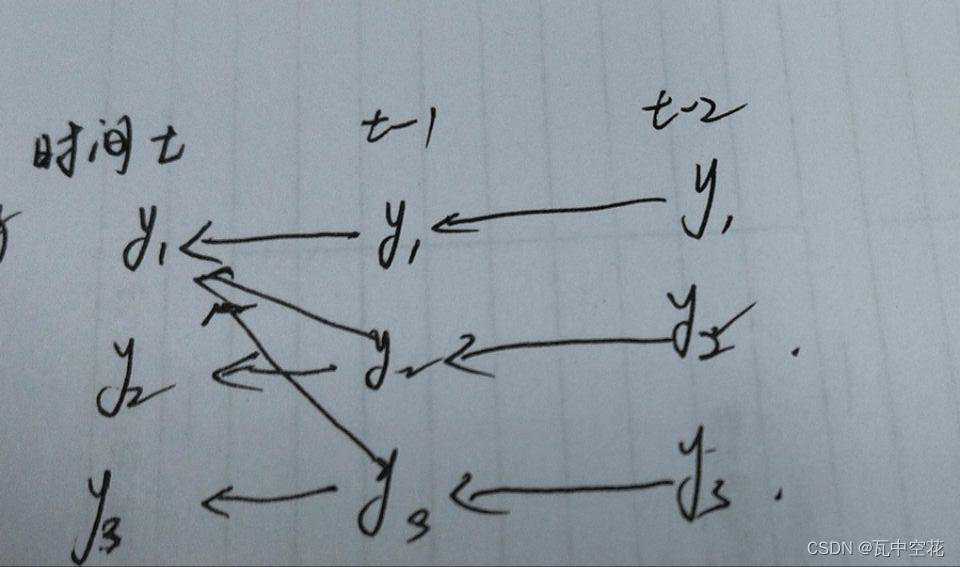
得出实验结果:
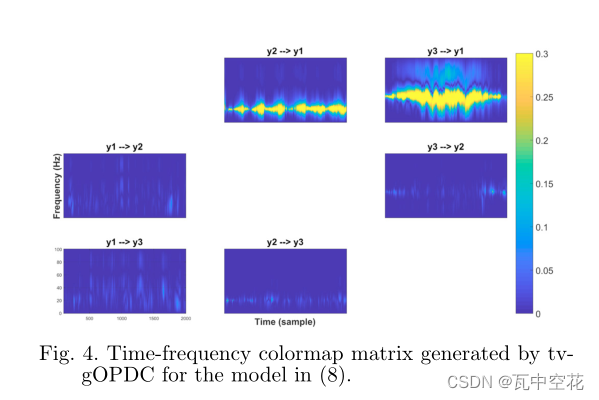
随时间变化,Granger因果大小在不断的变化。
当因果强度高于所有因果指数平均值时,认为存在格兰杰因果关系
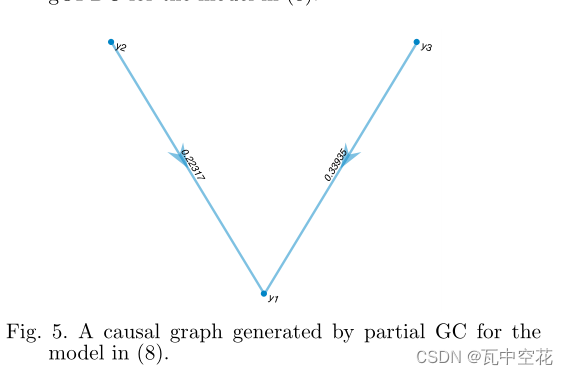
发现结果因果y2与y3对y1存在因果效应与之前的公式分析一致。
实验二:
在公共数据集上——田纳西-伊斯曼过程模拟。
IDV1 to IDV16故障已知,选IDV10作为实验对象构建一果图。因为它表示为过程中注入流4的C进料温度的随机变化,该故会导致非平稳过程。
首先用多向重建的贡献进行预处理,得到对故障IDV10贡献最大的变量。
具体MRBC的实现(需要对文章进行研究)。。。????
得到三个变量:Stripper Temp,XMV8,XMV7。
用 tv-gOPDC:一种可以研究非平稳时间序列数据因果关系分析的工具
当没有因果阀值时,可得:
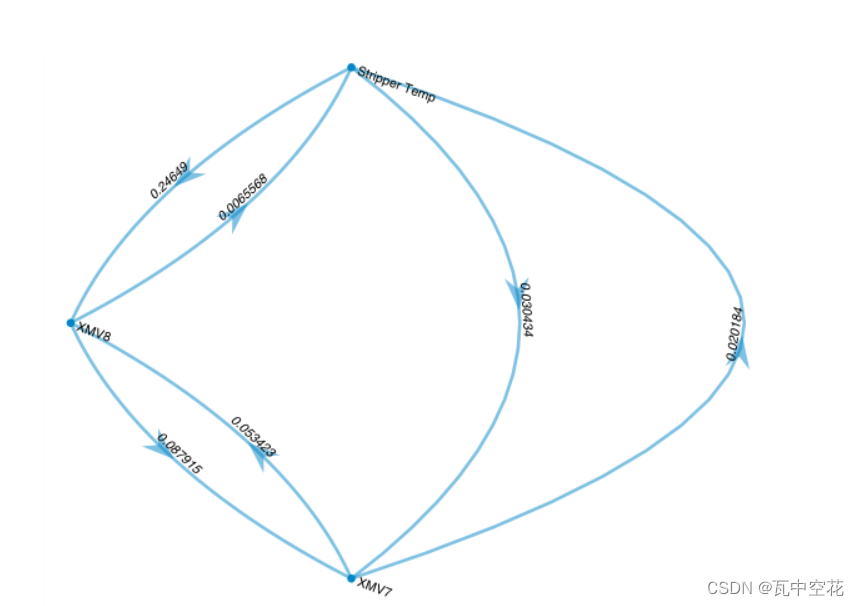
在平均因果阀值下,(提出疑问:阀值不一定是平均阀值吧,还有哪些方法呢?而且不通过阀值,是否可以通过其它系数进行区分?)
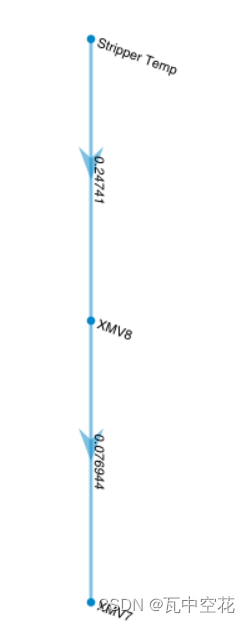
所以, C进料温度的升高将直接影响汽提塔的温度。
总结:
1.这是一篇应用性文章,未对GRanger因果进行方法性改进,更多是编写了一个应用程序。
没有接触过GRanger的可以看看,流程比较完备。
2.对Granger因果的溯源实现很简单,未进行推理量化,只是简单的得知此变量与其它变量有关。
但究竟有什么关系?关系强度多大?对预测有什么作用并未提及?
以及计算的因果指数强度大小和溯源的影响只是通过阀值简单排除,是否并不合理?
值得思考!