一、前言
该模型是和NFM模型结构上非常相似, 算是NFM模型的一个延伸,在NFM中, 不同特征域的特征embedding向量经过特征交叉池化层的交叉,将各个交叉特征向量进行“加和”, 然后后面跟了一个DNN网络, 这里面的问题是这个加和池化,它相当于“一视同仁”地对待所有交叉特征, 没有考虑不同特征对结果的影响程度,作者认为这可能会影响最后的预测效果, 因为不是所有的交互特征都能够对最后的预测起作用。 没有用的交互特征可能会产生噪声。
二、AFM模型原理
作者在提出NFM之后, 又对其进行了改进, 把注意力机制引入到了里面去, 来学习不同交叉特征对于结果的不同影响程度
AFM模型结构如下:
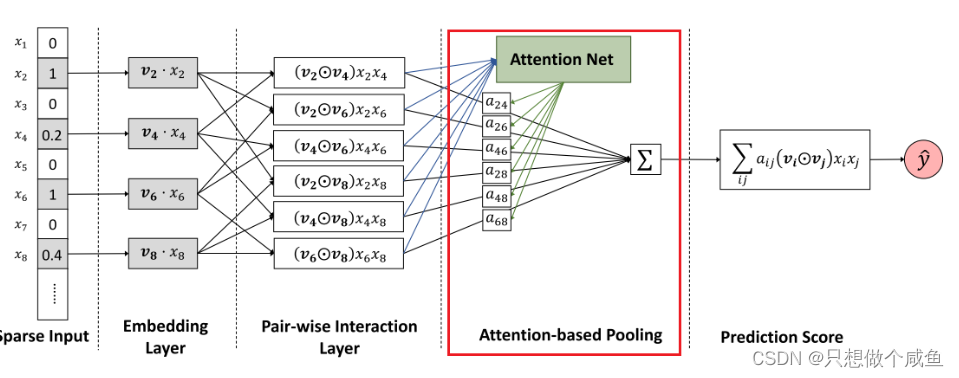
1、Input和embedding层
和NFM模型的一样,也是大部分深度学习模型的标配了, 这里为了简单,他们的输入把连续型的特征给省去了, 输入的是稀疏特征, 然后进入embedding层, 得到相应稀疏特征的embedding向量
2、Pair-wise Interaction Layer
这里和NFM是一样的,采用的也是每对Embedding向量进行各个元素对应相乘(element-wise product)交互, 这个和FM有点不太一样, 那里是每对embedding的内积, 而这里是对应元素相乘(不想加),这个要注意一下。 公式长下面这样子:

3、Attention based Pooling layer
本篇论文的一个核心创新 — Attention based Pooling layer。
这个想法是不同的特征交互向量在将它们压缩为单个表示时根据对预测结果的影响程度给其加上不同权重, 然后在对其进行求和。
计算公式如下:
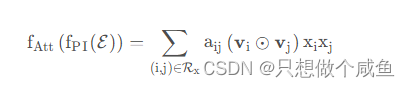
其中,表示
对的注意力分数, 表示该交互特征对于预测目标的重要性程度。为了解决泛化问题,这里才使用了一个多层感知器(MLP)将注意力得分参数化,就是上面的那个Attention Net。
该注意力网络的结构是一个简单的单全连接层加softmax输出层的结构, 数学表示如下:
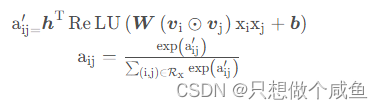
4、output
基于注意力的池化层的输出是一个k 维向量,该向量是所有特征交互向量根据重要性程度进行了区分了之后的一个聚合效果,然后我们将其映射到最终的预测得分中。所以AFM的总体公式如下:
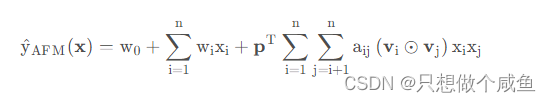
这个模型也是回归任务和分类任务皆可, 并且相对于NFM, 目前上面暂时没有用到DNN网络来学习高阶的交互了, 这个暂定为了作者未来的研究工作。
三、AFM的pytorch代码实现
老样子
1、DNN网络
(可以不加,加上效果更稳点,可以更好的处理高阶交互)
class Dnn(nn.Module):
def __init__(self, hidden_units, dropout=0.):
"""
hidden_units: 列表, 每个元素表示每一层的神经单元个数, 比如[256, 128, 64], 两层网络, 第一层神经单元128, 第二层64, 第一个维度是输入维度
dropout = 0.
"""
super(Dnn, self).__init__()
self.dnn_network = nn.ModuleList(
[nn.Linear(layer[0], layer[1]) for layer in list(zip(hidden_units[:-1], hidden_units[1:]))])
self.dropout = nn.Dropout(dropout)
def forward(self, x):
for linear in self.dnn_network:
x = linear(x)
x = F.relu(x)
x = self.dropout(x)
return x
2、Attention_layer网络
class Attention_layer(nn.Module):
def __init__(self, att_units):
"""
:param att_units: [embed_dim, att_vector]
"""
super(Attention_layer, self).__init__()
self.att_w = nn.Linear(att_units[0], att_units[1]) #8*8
self.att_dense = nn.Linear(att_units[1], 1) #8*1
def forward(self, bi_interaction): # bi_interaction (None, (field_num*(field_num-1)_/2, embed_dim)
a = self.att_w(bi_interaction) # (None, (field_num*(field_num-1)_/2, t) 这里是维度变化32*325*8→ 32*325*8
a = F.relu(a) # (None, (field_num*(field_num-1)_/2, t) 非线性激活
att_scores = self.att_dense(a) # (None, (field_num*(field_num-1)_/2, 1) 再次进行维度变化 32*325*8→ 32*325*1
att_weight = F.softmax(att_scores, dim=1) # (None, (field_num*(field_num-1)_/2, 1) 32*325*1 对分数进行0-1范围限定
att_out = torch.sum(att_weight * bi_interaction, dim=1) # (None, embed_dim) 32*325*8 求和后→32*8
return att_out
3、AFM网络
class AFM(nn.Module):
def __init__(self, feature_columns, mode, hidden_units, att_vector=8, dropout=0.5, useDNN=False):
"""
AFM:
:param feature_columns: 特征信息, 这个传入的是fea_cols array[0] dense_info array[1] sparse_info
:param mode: A string, 三种模式, 'max': max pooling, 'avg': average pooling 'att', Attention
:param att_vector: 注意力网络的隐藏层单元个数
:param hidden_units: DNN网络的隐藏单元个数, 一个列表的形式, 列表的长度代表层数, 每个元素代表每一层神经元个数, lambda文里面没加
:param dropout: Dropout比率
:param useDNN: 默认不使用DNN网络
"""
super(AFM, self).__init__()
self.dense_feature_cols, self.sparse_feature_cols = feature_columns
self.mode = mode
self.useDNN = useDNN
# embedding
self.embed_layers = nn.ModuleDict({
'embed_' + str(i): nn.Embedding(num_embeddings=feat['feat_num'], embedding_dim=feat['embed_dim'])
for i, feat in enumerate(self.sparse_feature_cols)
})
# 如果是注意机制的话,这里需要加一个注意力网络
if self.mode == 'att':
self.attention = Attention_layer([self.sparse_feature_cols[0]['embed_dim'], att_vector])
# 如果使用DNN的话, 这里需要初始化DNN网络
if self.useDNN:
# 这里要注意Pytorch的linear和tf的dense的不同之处, 前者的linear需要输入特征和输出特征维度, 而传入的hidden_units的第一个是第一层隐藏的神经单元个数,这里需要加个输入维度
self.fea_num = len(self.dense_feature_cols) + self.sparse_feature_cols[0]['embed_dim'] #13*8=21
hidden_units.insert(0, self.fea_num) #[21, 128, 64, 32]
self.bn = nn.BatchNorm1d(self.fea_num)
self.dnn_network = Dnn(hidden_units, dropout)
self.nn_final_linear = nn.Linear(hidden_units[-1], 1)
else:
self.fea_num = len(self.dense_feature_cols) + self.sparse_feature_cols[0]['embed_dim']
self.nn_final_linear = nn.Linear(self.fea_num, 1)
def forward(self, x):
dense_inputs, sparse_inputs = x[:, :len(self.dense_feature_cols)], x[:, len(self.dense_feature_cols):]
sparse_inputs = sparse_inputs.long() # 转成long类型才能作为nn.embedding的输入
sparse_embeds = [self.embed_layers['embed_' + str(i)](sparse_inputs[:, i]) for i in
range(sparse_inputs.shape[1])]
sparse_embeds = torch.stack(sparse_embeds) # embedding堆起来, (field_dim, None, embed_dim) 26*32*8
sparse_embeds = sparse_embeds.permute((1, 0, 2)) #32*26*8
# 这里得到embedding向量之后 sparse_embeds(None, field_num, embed_dim)
# 下面进行两两交叉, 注意这时候不能加和了,也就是NFM的那个计算公式不能用, 这里两两交叉的结果要进入Attention
# 两两交叉enbedding之后的结果是一个(None, (field_num*field_num-1)/2, embed_dim)
# 这里实现的时候采用一个技巧就是组合
# 比如fild_num有4个的话,那么组合embeding就是[0,1] [0,2],[0,3],[1,2],[1,3],[2,3]位置的embedding乘积操作
first = []
second = []
for f, s in itertools.combinations(range(sparse_embeds.shape[1]), 2): #这里就是从前面的(0-26) 产生2配对 n*(n-1)/2
first.append(f) #325
second.append(s) #325
# 取出first位置的embedding 假设field是3的话,就是[0, 0, 0, 1, 1, 2]位置的embedding
p = sparse_embeds[:, first, :] # (None, (field_num*(field_num-1)_/2, embed_dim)
q = sparse_embeds[:, second, :] # (None, (field_num*(field_num-1)_/2, embed_dim)
bi_interaction = p * q # (None, (field_num*(field_num-1)_/2, embed_dim) 32*325*8
if self.mode == 'max':
att_out = torch.sum(bi_interaction, dim=1) # (None, embed_dim)
elif self.mode == 'avg':
att_out = torch.mean(bi_interaction, dim=1) # (None, embed_dim)
else:
# 注意力网络
att_out = self.attention(bi_interaction) # (None, embed_dim) 32*8
# 把离散特征和连续特征进行拼接
x = torch.cat([att_out, dense_inputs], dim=-1) #32*21
if not self.useDNN:
outputs = F.sigmoid(self.nn_final_linear(x))
else:
# BatchNormalization
x = self.bn(x)
# deep
dnn_outputs = self.nn_final_linear(self.dnn_network(x)) #32*1
outputs = F.sigmoid(dnn_outputs)
return outputs补充:
1、产生组合排列(两两特征交叉)如下部分需要注意
first = []
second = []
for f, s in itertools.combinations(range(sparse_embeds.shape[1]), 2): #这里就是从前面的(0-26) 产生2配对 n*(n-1)/2
first.append(f) #325
second.append(s) #325
# 取出first位置的embedding 假设field是3的话,就是[0, 0, 0, 1, 1, 2]位置的embedding
p = sparse_embeds[:, first, :] # (None, (field_num*(field_num-1)_/2, embed_dim)
q = sparse_embeds[:, second, :] # (None, (field_num*(field_num-1)_/2, embed_dim)
bi_interaction = p * q # (None, (field_num*(field_num-1)_/2, embed_dim) 32*325*8这里没有采用这种for循环,才是采用了排列组合的方式,求得组合数,然后选出相应位置的embedding,最后相乘得到的。 假设有4个特征embedding的话,下标位置是[0,1,2,3], 考虑两两位置交叉, 那么位置就是[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]的6种交叉,这个会发现正好是个组合数, 我们直接用itertools.combinations函数产生上面的组合数,然后把左边位置上的这些embedding存到一个p矩阵, 右边位置上的embedding存入一个q矩阵, 然后两者对应位置的embedding相乘就是交叉结果了。 这样应该会快不少
2、对于注意力的理解
att_scores = self.att_dense(a) #32*325*132是我们的这一批次训练数量, 325是两两交互的特征 ,1是维度
可以理解为 某一个样本(共32样本),对这325个排列组合的感兴趣程度,1维(n维也一样)就是表示具体的权重值。
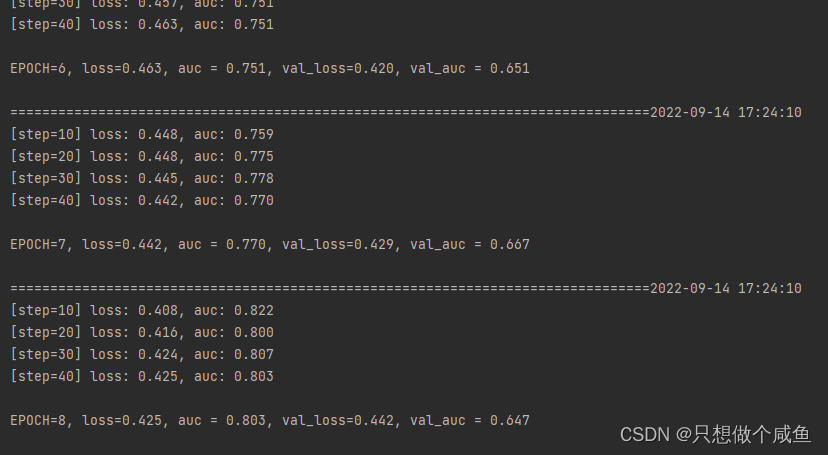
4、模型训练
总结
解决的痛点问题是各个特征交叉之后的embedding向量被同等看待,赋予对预测相同重要性的问题, 所以这里加了一个注意力机制,给各个特征交叉后的embedding向量不同的权重,这样表示了他们对预测结果的重要程度。