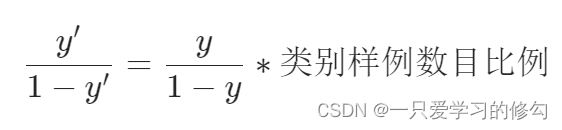目录
线性判别分析(Linear Discriminant Analysis /LDA)
基本形式
线性模型常表示为:
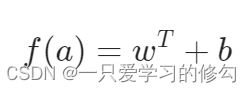
学习过程即是获取w以及b 的过程。
线性回归
属性表示
对于离散属性:
存在序的关系的,如“ 高,中 ,低 ”,可表示为:

不存在序的关系的,如“ 学生 ,老师 ”,可表示为:
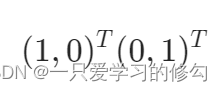
误差损失
常使用均方误差(square loss):
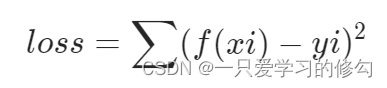
使loss对w以及b分别求导,令求导式都为0,通常可以求得w以及b 的最优解。
广义线性模型
通过联系函数将线性模型与目标联系起来,例如:
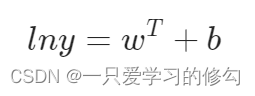
此时输出输出的空间映射是非线性的,对数函数即起到了联系作用。
对数几率回归
引入一个单调可微函数,使得线性模型能够用于分类问题。
对数几率函数(logistic function)可以实现将Z值转化为0到1之间的y值:
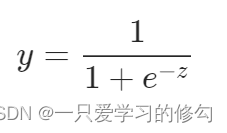
实际是一种分类方法,还能够近似概率,辅助决策。
线性判别分析(Linear Discriminant Analysis /LDA)
将样例投影到设定的一条直线上,同类点尽可能接近,异类点尽可能远离。分类点的位置用于进行分类。
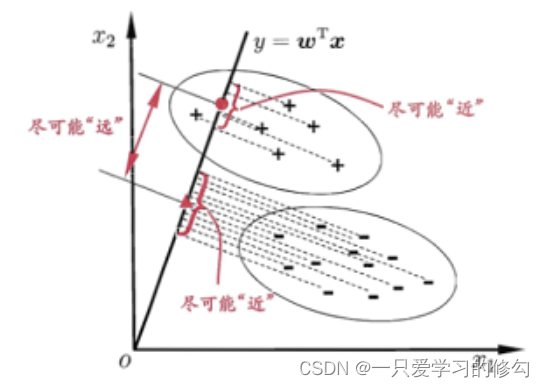
希望使得同类样例尽可能接近,异类样例尽可能远离,目标函数:
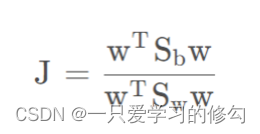
Sb为类间散度矩阵,Sw为类内散度矩阵,此处不展开。
多分类学习
基本的学习思路是进行拆解,将多分类问题拆解成多个二分类问题。常用的策略如下:
一对一(one VS one/OVO )
将N个类别两两配对进行二分类,多组投票结果作为多分类结果
一对其他(one VS rest/OVR)
将一个类别与其他所有类别进行配对进行二分类,多组投票结果作为多分类结果
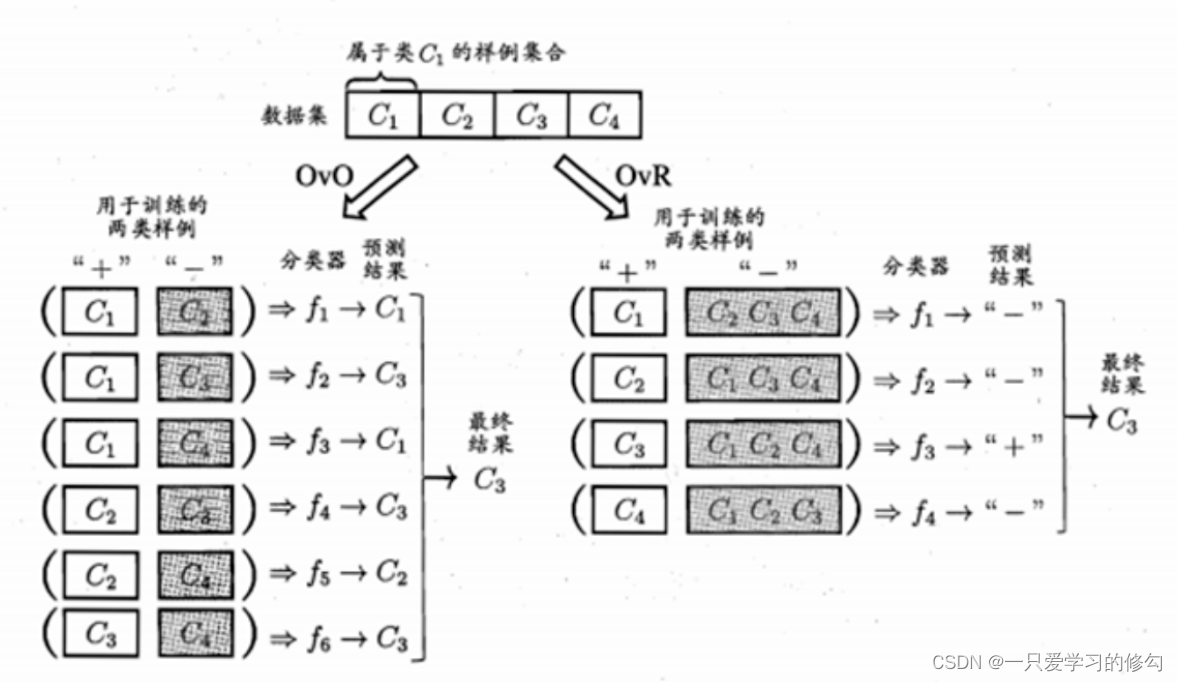
ovo使用更多的分类器,而ovr每次都需要使用所有的样例,多类别时,时间开销OVO较小,多数情况下差不多。
多对多(many vs many /MVM)
多用纠错输出码(ECOC)进行类别拆分,在编码矩阵中通过距离判定最终分类结果,此处不展开。
类别不平衡
对线性模型,不同类别的样例数量差距过大,学习结果可能不具有价值。
解决手法常见有:
欠采样(undersampling)
去除过多的样例使得正反例数目接近
过采样(oversampling)
增加较少的样例使得正反例数目接近
阈值移动(threshold-moving)
直接使用不平衡的类别样例进行学习,训练好的分类器在进行决策的时候,嵌入缩放式: