跟随carl代码随想录刷题
语言：python

110. 平衡二叉树

题目：给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
👉示例1：

输入：root = [3,9,20,null,null,15,7]
输出：true
👉示例2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
👉示例 3：
输入：root = []
输出：true

题目分析

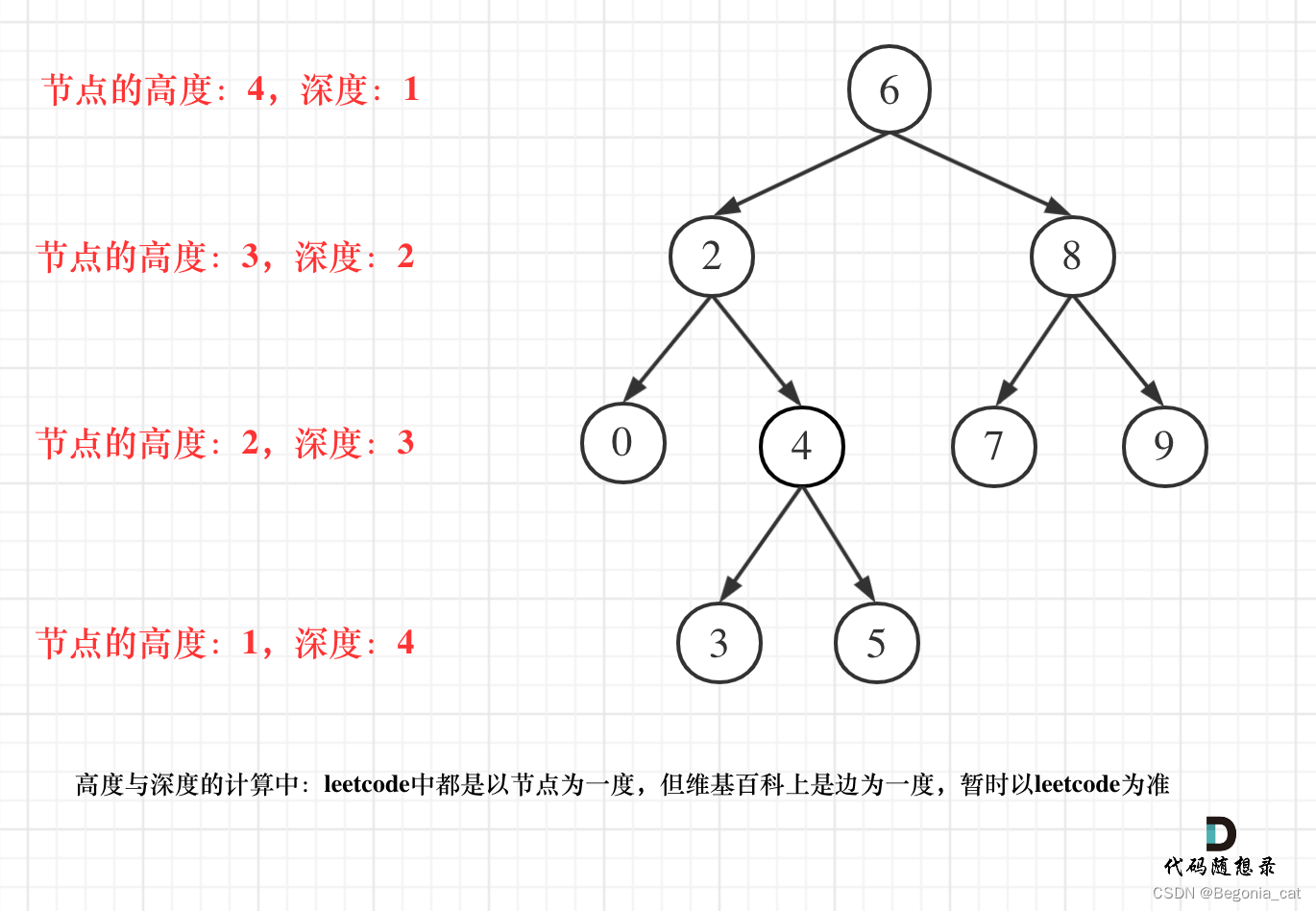
• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。

  • 求深度可以从上到下去查 所以需要前序遍历（中左右）

• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

  • 而高度只能从下到上去查，所以只能后序遍历（左右中）

• 二叉树的最大深度即根节点的高度

但leetcode中强调的深度和高度很明显是按照节点来计算的，如图：

完整代码如下

因为求高度平衡，所以用后序遍历

后序遍历——递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        if self.getHeight(root) != -1:
            return True
        else:
            return False

    def getHeight(self, root):
        if not root:
            return 0  # 终止条件：遇到空节点后返回0
        leftHeight = self.getHeight(root.left)
        if leftHeight == -1: return -1
        rightHeight = self.getHeight(root.right)
        if rightHeight == -1:return -1

        if abs(leftHeight - rightHeight) > 1:
            return -1  # -1表示不是平衡二叉树
        else:
            return 1 + max(leftHeight, rightHeight)  # 以当前节点为根节点的最大高度
        

后序遍历——迭代法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True
        
        height_map = {}
        stack = [root]

        while stack:  # 后序遍历
            node = stack.pop()
            if node:
                stack.append(node)  # 中
                stack.append(None)
                if node.right:
                    stack.append(node.right)  # 右
                if node.left:
                    stack.append(node.left)  # 左
                
            else:
                real_node = stack.pop()
                left, right = height_map.get(real_node.left, 0), height_map.get(real_node.right, 0)
                print(height_map)
                if abs(left-right)>1:
                    return False
                height_map[real_node] = 1 + max(left, right)
        return True

查看一下height_map信息：

{}
{TreeNode{val: 9, left: None, right: None}: 1}
{TreeNode{val: 9, left: None, right: None}: 1, TreeNode{val: 15, left: None, right: None}: 1}
{TreeNode{val: 9, left: None, right: None}: 1, TreeNode{val: 15, left: None, right: None}: 1, TreeNode{val: 7, left: None, right: None}: 1}
{TreeNode{val: 9, left: None, right: None}: 1, TreeNode{val: 15, left: None, right: None}: 1, TreeNode{val: 7, left: None, right: None}: 1, TreeNode{val: 20, left: TreeNode{val: 15, left: None, right: None}, right: TreeNode{val: 7, left: None, right: None}}: 2}