1.栈

1.1栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。 进行数据插入和删除操作的一端 称为栈顶，另一端称为栈底。 栈中的数据元素遵守后进先出 LIFO （ Last In First Out）的原则。

压栈：栈的插入操作叫做进栈 / 压栈 / 入栈， 入数据在栈顶 。

出栈：栈的删除操作叫做出栈。 出数据也在栈顶 。

1.2栈的实现

栈的实现一般可以使用 数组或者链表实现 ，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

// 支持动态增长的栈

typedef int STDataType ;

typedef struct Stack

{

        STDataType * _a ;

        int _top ; // 栈顶

        int _capacity ; // 容量

} Stack ;

// 初始化栈

void StackInit ( Stack * ps );

// 入栈

void StackPush ( Stack * ps , STDataType data );

// 出栈

void StackPop ( Stack * ps );

// 获取栈顶元素

STDataType StackTop ( Stack * ps );

// 获取栈中有效元素个数

int StackSize ( Stack * ps );

// 检测栈是否为空，如果为空返回非零结果，如果不为空返回 0

int StackEmpty ( Stack * ps );

// 销毁栈

void StackDestroy ( Stack * ps );

// 初始化栈 
void StackInit(Stack* ps)
{
	assert(ps);
	ps->_a = NULL;
	ps->_top = 0;
	ps->_capacity = 0;
}
// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
	if (ps->_capacity == ps->_top )
	{
		int newcapacity =ps->_capacity== 0 ? 4 : ps->_capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->_a, sizeof(STDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc ::");
			exit(-1);
		}
		ps->_a = tmp;
		ps->_capacity = newcapacity;
	}
	ps->_a[ps->_top] = data;
	ps->_top++;
}
// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	ps->_top--;
}
// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->_a[ps->_top-1];
}
// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->_top;
}
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->_top == 0;
}
// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->_a);
	ps->_a = NULL;
	ps->_top = ps->_capacity = 0;
}

2.队列

2.1队列的概念及结构

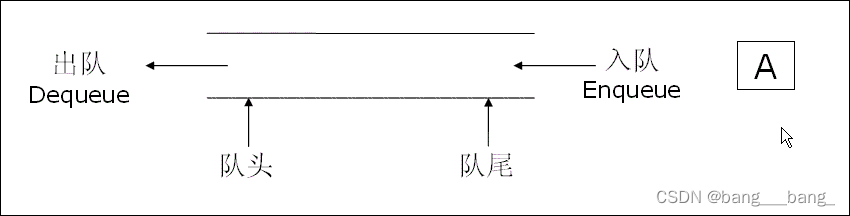
队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出 FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾出队列：进行删除操作的一端称为 队头。

2.2队列的实现

队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低。

// 链式结构：表示队列

typedef struct QListNode

{

        struct QListNode * _next ;

        QDataType _data ;

} QNode ;

// 队列的结构

typedef struct Queue

{

        QNode * _front ;

        QNode * _rear ;

} Queue ;

// 初始化队列

void QueueInit ( Queue * q );

// 队尾入队列

void QueuePush ( Queue * q , QDataType data );

// 队头出队列

void QueuePop ( Queue * q );

// 获取队列头部元素

QDataType QueueFront ( Queue * q );

// 获取队列队尾元素

QDataType QueueBack ( Queue * q );

// 获取队列中有效元素个数

int QueueSize ( Queue * q );

// 检测队列是否为空，如果为空返回非零结果，如果非空返回 0

int QueueEmpty ( Queue * q );

// 销毁队列

void QueueDestroy ( Queue * q );

// 初始化队列 
void QueueInit(Queue* q)
{
	assert(q);
	q->_front = q->_rear = NULL;
}
// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc faile!\n");
		exit(-1);
	}
	newnode->_data = data;
	newnode->_next = NULL;
	if (q->_front ==NULL)
	{
		q->_front = q->_rear = newnode;
	}
	else
	{
		q->_rear->_next = newnode;
		q->_rear = q->_rear->_next;
	}
}
// 队头出队列 
void QueuePop(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	//1.1个结点
	//2.多个结点
	if (q->_front->_next == NULL)
	{
		free(q->_front);
		q->_front = q->_rear = NULL;
	}
	else
	{
		QNode* next = q->_front->_next;
		free(q->_front);
		q->_front = next;
	}
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->_front->_data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->_rear->_data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);
	int  size = 0;
	QNode* cur = q->_front;
	while (cur)
	{
		++size;
		cur = cur->_next;
	}
	return size;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
bool QueueEmpty(Queue* q)
{
	assert(q);
	return q->_front == NULL;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* cur = q->_front;
	while (cur)
	{
		QNode* next = cur->_next;
		free(cur);
		cur = next;
	}
	q->_front =q->_rear= NULL;
}

2.3循环队列

实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型

时可以就会使用循环队列。环形队列可以使用数组实现，也可以使用循环链表实现。

循环队列OBJ

这里我们采用数组的方式实现循环队列，多开辟一个数组空间用来区分满状态和空状态的条件不同。需要注意在入队列的时候，如果越过数组需要把下标置回开头，入一个数据rear向后移1。

出队列的时候，只需要把head向后移1，与入队列一样需要注意越过数组置回0。

队尾元素是rear前一个位置，需要判断当rear在0处时，将rear置到k+1处，再访问前一个位置即可。

typedef struct {
    int k;
    int head;
    int tail;
    int *a;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->k=k;
    obj->head=obj->tail=0;
    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->head==obj->tail;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    int next=obj->tail+1;
    if(next==obj->k+1)
        next=0;
    return next==obj->head;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;
    obj->a[obj->tail]=value;
    obj->tail++;
    if(obj->tail==obj->k+1)
        obj->tail=0;
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;
    obj->head++;
    if(obj->head==obj->k+1)
        obj->head=0;
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    return obj->a[obj->head];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    int prev=obj->tail;
    if(prev==0)
        prev=obj->k+1;
    return obj->a[prev-1];
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
    obj==NULL;
}

拓展：栈可以通过2个队列来回倒数据模拟实现。OBJ

队列可以通过2个栈，1个当压栈，1个当出栈模拟实现。OBJ

本文含有隐藏内容，请开通VIP 后查看

《数据结构》——栈和队列

1.栈

1.1栈的概念及结构

1.2栈的实现

2.队列

2.1队列的概念及结构

2.2队列的实现

2.3循环队列

网站公告

今日签到

热门文章

最新发布