课程主页:CS224W | Home
课程视频链接:【双语字幕】斯坦福CS224W《图机器学习》课程(2021) by Jure Leskovec
文章目录
1 前言
在我们的印象中,网络通常是这个样子的,就像社交网络一样:由许多个节点团(社团)联系而成,节点团内的节点联系紧密,节点团之间的节点联系稀疏。

这一节的内容就是来探讨怎样去自动发掘网络中的社团(Community)。
2 预备知识和案例
2.1 弱连接理论
弱连接理论由美国社会学家马克·格拉诺维特(mark granovetter)于1974年提出。
格兰诺维特指出:在传统社会,每个人接触最频繁的是自己的亲人、同学、朋友,这是一种十分稳定的然而传播范围有限的社会认知,这是一种"强连接" (strong ties)现象;同时,还存在另外一类相对于前一种社会关系更为广泛的,然而却是肤浅的社会认知。例如一个被人无意间被人提到或者打开收音机偶然听到的一个人,格兰诺维特把后者称为"弱连接"(weak ties)。
研究发现:其实与一个人的工作和事业关系最密切的社会关系并不是"强连接",而常常是"弱连接"。一个人的亲朋好友圈子里的人可能相互认识,因此,在这样圈子中,他人提供的交流信息总是冗余。比如,我从这个朋友或亲戚听到的,可能早已经在另一个朋友那里听说了,而他们之间也都相互交谈过此话题。日常生活中不乏这样的事例。
弱链接在我们与外界交流时发挥了关键的作用,为了得到新的信息,我们必须充分发挥弱链接的作用。这些弱链接,或是熟人,都是我们与外界沟通的桥梁,不同地方的人通过弱链接可以得到不同的信息。最亲近的朋友可能生活圈子和你差不多,你们的生活几乎完全重合。而那些久不见面的人,他们可能掌握了很多你并不了解的情况。只有这些"微弱关系"的存在,信息才能在不同的圈子中流传。弱链接的威力正在于此。
总结:从信息获取的角度上看,长范围的关系(弱连接)可以帮助我们获取更丰富的、更不同的、更新的信息;而经常联系的密友(强连接)会形成一个圈子,大家获取信息的来源是大致是一样的,从信息获取的角度来说是冗余的——这就解释了为什么我们会选择从熟人而不是密友那里获取信息。
2.2 三元闭包(triadic closure)

解释:如果B和C都认识A,那么B认识C的机会增加,B和C的信任增加,A使B和C共处的动机增加。
2.3 边重合(Edge Overlap)
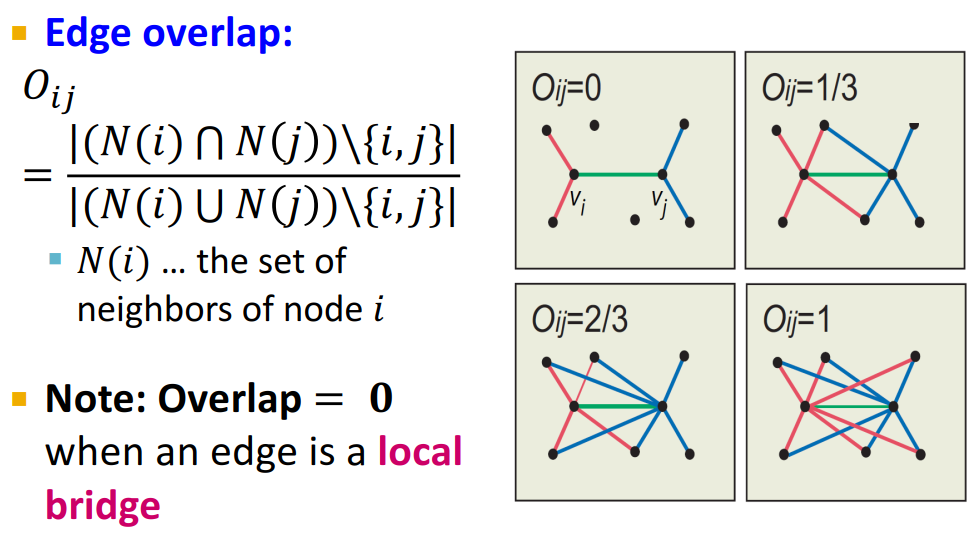
边重合度Oij:分子是与节点i和节点j共有邻居的数量,分母是节点i和节点j所有邻居的数量。
即:两点的共同邻居在它们所有邻居中的占比,表示了两个人社交圈子的重合程度。
- 当两个节点的Overlap=0,即没有共同邻居时,说明两个节点之间是“弱连接”;
- 当两个节点的Overlap=1时,说明两个节点之间是“强连接”。
2.4 通话网络(边的重合度 vs. 边的强度)

从上图中可以看出:
- 蓝线是真实的通话网络,边的重合度(通讯录中共同好友的数量)越高,边的强度(彼此打电话的概率),即边的重合度和边的强度成正比关系。
- 红色的是保持网络结构不变,给网络中的节点随机分配边的强度之后统计的边的重合度,会发现朋友的重合度与联系的紧密程度无关了,几乎是一条水平直线。
除此之外,如果我们按照“边的strength”(左图)或“边的overlap”(右图)两个指标的高低逐渐移除通话网络中的边,其最大连通子图的减小快慢也是不同的,如下图所示: 
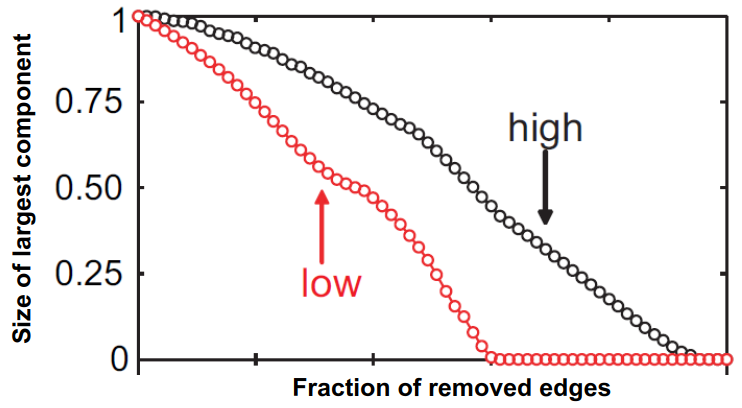
从图中可以看出:
- 左图中,移除低stength(通话次数更少)的边,最大连通子图减小的更快,网络崩溃的更快;
- 右图中,移除低overlap(共同好友更少)的边,最大连通子图减小的更快,网络崩溃的更快;
2.5 小结
通话网络的案例指出,强连接的边重合度也很高,能形成更加紧密连接的社团(Community),弱连接的边重合度不高,但在整个社交网络中有着更为关键的作用。同时,这些例子也说明了网络(Netwoks)中普遍存在集群的现象。

3 社团发现
根据前文Granovetter的理论,网络是由紧密相连的节点组成的。而Community是具有大量内部连通性很强的节点和较少外部连通性较弱的节点组成。
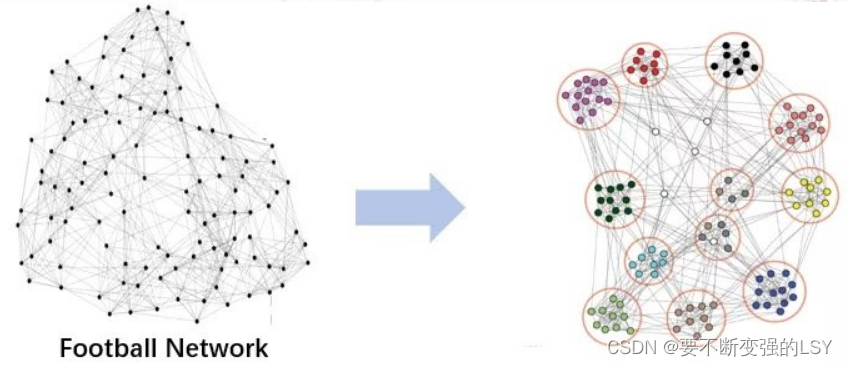
下图中表示的是从众多球队组成的网络中找到同属于一个部门的球队。那么,怎样去自动检测到网络中有密切联系的Community呢?这就是我们本篇要研究的重头戏——社团发现。
3.1 评价指标
定义:
- 模块化程度
(用来度量一个网络划分成社团的程度)
- 互不相交的分组s(S表示所有分组的集合)

思想:一个社团内部的连接要比随机生成的连接情况下更紧密。
解释:s组内实际边的数量和随机生成的s组内边的数量之间的差值代表s组中节点的紧密程度,而这个差值和参数Q成正比,所以就可以用Q来衡量一个社团的紧密程度。
那么,如何随机构造一个新的Null Model呢?如下图,新网络和原网络的每个节点有相同的度数分布,是一个允许有重边和自环的多重图。

在这个新的网络中,两个节点间预期存在的边可以由下面的公式计算:
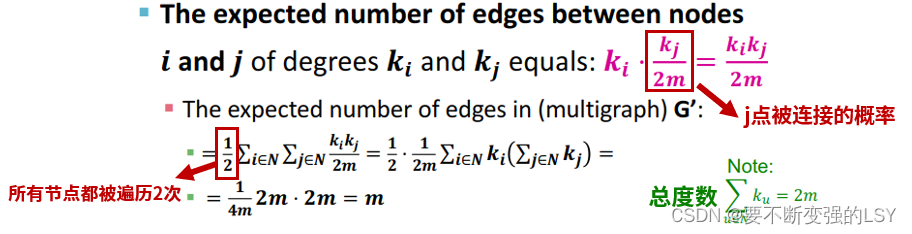
最后经过计算验证,整个图的边数依然是m,证明我们的新网络
是合理的。
这样,我们最后就得到了Modularity 的计算公式:

- 归一化处理后的 Q 的取值在-1到1之间
- 如果划分的分组内节点之间的边数大于预期的边数,则 Q 为正
- 通常来时,Q 值越大,发现的社团内部连接越紧密,效果越好
- 在实际情况中,大多数网络在划分后的 Q 值出现在0.3-0.7之间表示社团发现的结果较好
上面Q值计算的公式等价于下面这个式子:

可以发现,计算模块度 Q 可以衡量目前的社团划分是否合理,那么,怎么找到社团呢?自然可以通过最大化 Q 值来发现社团。这就是接下来要介绍的社团发现算法——Louvain算法的思想。
3.2 非重叠社团发现算法——Louvain算法
Louvain算法是一种贪心算法,被广泛应用于非重叠社团发现。
3.2.1 算法优点
- 时间复杂度为
(n为节点数)
- 支持权重图
- 能找出分层的社团结果(hierarchical communities),可根据需要选择层级。
- 适用于研究大型网络,因为它速度快,收敛快,高模块化输出。
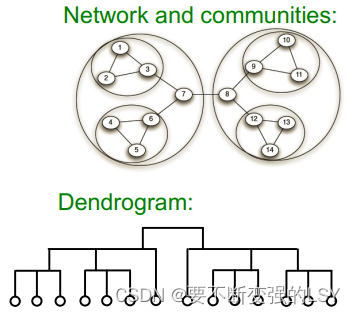
3.2.2 算法过程
整体过程分为三步:
第一步:以最大化为原则进行社团划分
- 将图中的每一个节点看作一个单独的社团;
- 遍历该图中的每一个节点
,进行以下两个计算:
① 将节点放入其邻居节点
所在的社团中,并计算此时的模块度变化值
② 将节点移动到能产生最大
的节点
所在的社团
3. 重复以上步骤直到没有节点移动(即不再增大)为止。
第二步:按照划分结果进一步构建新网络
将第一步识别出的一个个社团聚合为一个个超级节点(super-nodes)以构建新的网络,这时边的权重为两个社团内所有原始结点的边权重之和。
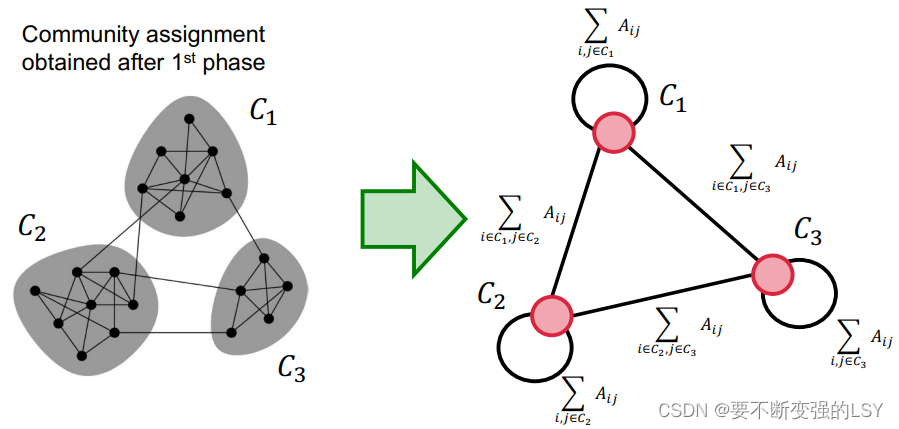
第三步:回到步骤一,循环迭代以上两个步骤直至算法稳定
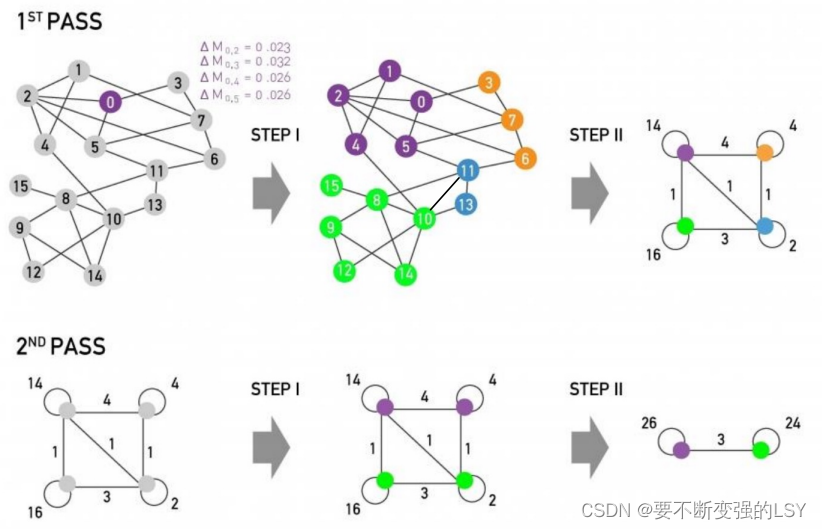
注:在第一步计算时,选取节点的顺序对最终结果是有影响的,但不显著。
3.2.3 ΔQ值的计算过程详解
在该算法的第一步中,要将节点移动到能产生最大
值的社团中,那么在将节点
从社团D移动到社团C的过程中,
值由以下两个部分组成:
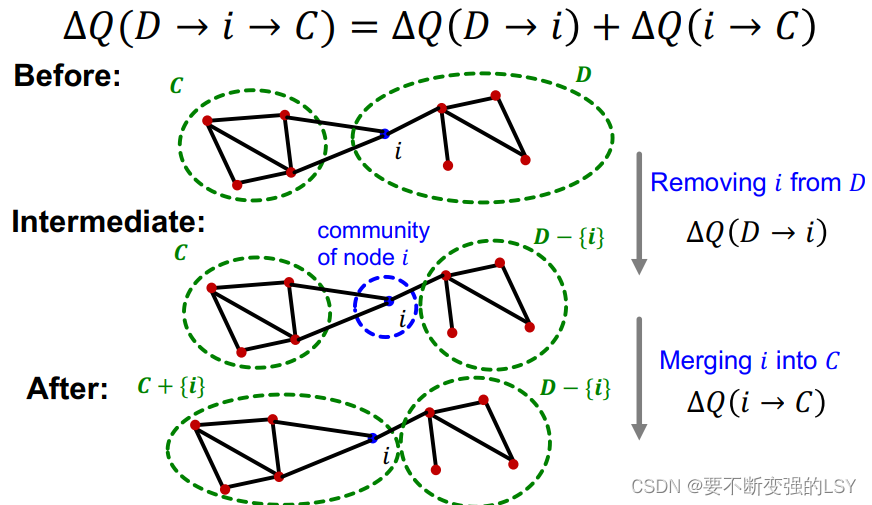
我们不仅要计算将节点加入社团C的
,还要计算将节点
移除社团D所产生的
。
接下来,具体推导一下的计算过程:
先定义关于社团C的两个量:
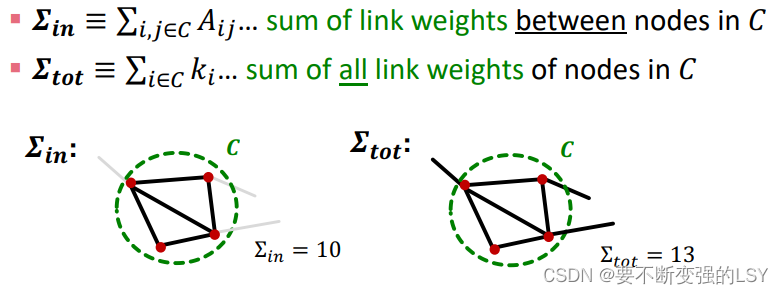
根据Q值的计算公式,可以得到社团C的Q:

接着,我们再定义将节点i加入社团C过程中涉及到的两个量:
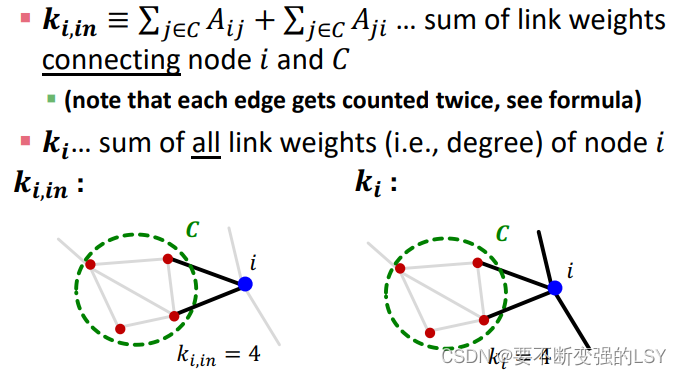
那么就可以得到节点i加入社团C前后的Q值:
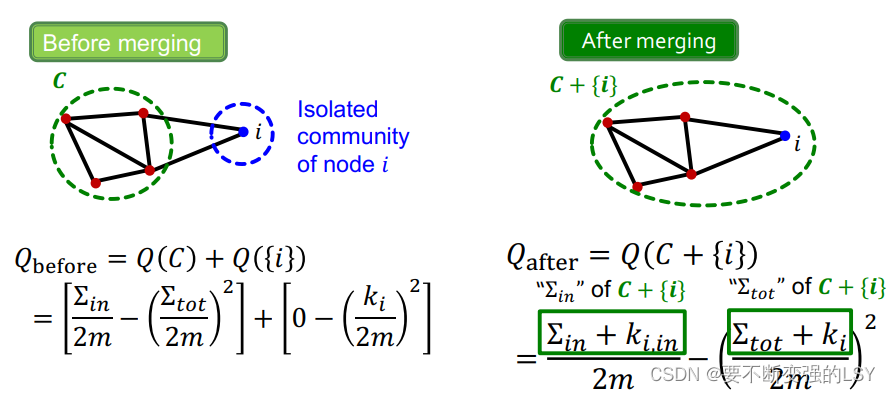
最后,我们就得到了以及整个
的计算公式:

最后,我们将反复循环迭代直到不再变化,即没有节点再移动:

该算法的伪代码如下:

4 总结
本篇笔记主要介绍了以下两个方面:
- Modularity
:用来度量一个网络划分成社团的程度,并决定着网络中社团数量的多少;
- Louvain算法:一种能在较大规模的非重叠网络上发现社团且结果较好的贪心算法。