A. Turtle Puzzle: Rearrange and Negate
Problem Statement
You are given an array a a a of n n n integers. You must perform the following two operations on the array (the first, then the second):
- Arbitrarily rearrange the elements of the array or leave the order of its elements unchanged.
- Choose at most one contiguous segment of elements and replace the signs of all elements in this segment with their opposites. Formally, you can choose a pair of indices l , r l, r l,r such that 1 ≤ l ≤ r ≤ n 1 \le l \le r \le n 1≤l≤r≤n and assign a i = − a i a_i = -a_i ai=−ai for all l ≤ i ≤ r l \le i \le r l≤i≤r (negate elements). Note that you may choose not to select a pair of indices and leave all the signs of the elements unchanged.
What is the maximum sum of the array elements after performing these two operations (the first, then the second)?
Input
The first line of the input contains a single integer t t t ( 1 ≤ t ≤ 1000 1 \le t \le 1000 1≤t≤1000) — the number of test cases. The descriptions of the test cases follow.
The first line of each test case contains a single integer n n n ( 1 ≤ n ≤ 50 1 \le n \le 50 1≤n≤50) — the number of elements in array a a a.
The second line of each test case contains n n n integers a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an ( − 100 ≤ a i ≤ 100 -100 \le a_i \le 100 −100≤ai≤100) — elements of the array.
Output
For each test case, output the maximum sum of the array elements after sequentially performing the two given operations.
Example
Example
| input |
|---|
| 8 |
| 3 |
| -2 3 -3 |
| 1 |
| 0 |
| 2 |
| 0 1 |
| 1 |
| -99 |
| 4 |
| 10 -2 -3 7 |
| 5 |
| -1 -2 -3 -4 -5 |
| 6 |
| -41 22 -69 73 -15 -50 |
| 12 |
| 1 2 3 4 5 6 7 8 9 10 11 12 |
| output |
|---|
| 8 |
| 0 |
| 1 |
| 99 |
| 22 |
| 15 |
| 270 |
| 78 |
Note
In the first test case, you can first rearrange the array to get [ 3 , − 2 , − 3 ] [3,-2,-3] [3,−2,−3] (operation 1), then choose l = 2 , r = 3 l = 2, r = 3 l=2,r=3 and get the sum 3 + − ( ( − 2 ) + ( − 3 ) ) = 8 3 + -((-2) + (-3)) = 8 3+−((−2)+(−3))=8 (operation 2).
In the second test case, you can do nothing in both operations and get the sum 0 0 0.
In the third test case, you can do nothing in both operations and get the sum 0 + 1 = 1 0 + 1 = 1 0+1=1.
In the fourth test case, you can first leave the order unchanged (operation 1), then choose l = 1 , r = 1 l = 1, r = 1 l=1,r=1 and get the sum − ( − 99 ) = 99 -(-99) = 99 −(−99)=99 (operation 2).
In the fifth test case, you can first leave the order unchanged (operation 1), then choose l = 2 , r = 3 l = 2, r = 3 l=2,r=3 and get the sum 10 + − ( ( − 2 ) + ( − 3 ) ) + 7 = 22 10 + -((-2) + (-3)) + 7 = 22 10+−((−2)+(−3))+7=22 (operation 2).
In the sixth test case, you can first leave the order unchanged (operation 1), then choose l = 1 , r = 5 l = 1, r = 5 l=1,r=5 and get the sum − ( ( − 1 ) + ( − 2 ) + ( − 3 ) + ( − 4 ) + ( − 5 ) ) = 15 -((-1)+(-2)+(-3)+(-4)+(-5))=15 −((−1)+(−2)+(−3)+(−4)+(−5))=15 (operation 2).
Solution
具体见文后视频。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
const int MAXN = 55;
int N;
int A[MAXN];
void solve()
{
cin >> N;
for (int i = 1; i <= N; i ++)
cin >> A[i];
sort(A + 1, A + 1 + N);
for (int i = 1; i <= N; i ++)
if (A[i] < 0)
A[i] = -A[i];
int Sum = 0;
for (int i = 1; i <= N; i ++)
Sum += A[i];
cout << Sum << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
B. Turtle Math: Fast Three Task
Problem Statement
You are given an array a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an.
In one move, you can perform either of the following two operations:
- Choose an element from the array and remove it from the array. As a result, the length of the array decreases by 1 1 1;
- Choose an element from the array and increase its value by 1 1 1.
You can perform any number of moves. If the current array becomes empty, then no more moves can be made.
Your task is to find the minimum number of moves required to make the sum of the elements of the array a a a divisible by 3 3 3. It is possible that you may need 0 0 0 moves.
Note that the sum of the elements of an empty array (an array of length 0 0 0) is equal to 0 0 0.
Input
The first line of the input contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \le t \le 10^4 1≤t≤104) — the number of test cases.
The first line of each test case contains a single integer n n n ( 1 ≤ n ≤ 1 0 5 1 \le n \le 10^5 1≤n≤105).
The second line of each test case contains n n n integers a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an ( 1 ≤ a i ≤ 1 0 4 1 \le a_i \le 10^4 1≤ai≤104).
The sum of n n n over all test cases does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.
Output
For each test case, output a single integer: the minimum number of moves.
Example
Example
| input |
|---|
| 8 |
| 4 |
| 2 2 5 4 |
| 3 |
| 1 3 2 |
| 4 |
| 3 7 6 8 |
| 1 |
| 1 |
| 4 |
| 2 2 4 2 |
| 2 |
| 5 5 |
| 7 |
| 2 4 8 1 9 3 4 |
| 2 |
| 4 10 |
| output |
|---|
| 1 |
| 0 |
| 0 |
| 1 |
| 1 |
| 2 |
| 1 |
| 1 |
Note
In the first test case, initially the array a = [ 2 , 2 , 5 , 4 ] a = [2, 2, 5, 4] a=[2,2,5,4]. One of the optimal ways to make moves is:
- remove the current 4 4 4th element and get a = [ 2 , 2 , 5 ] a = [2, 2, 5] a=[2,2,5];
As a result, the sum of the elements of the array a a a will be divisible by 3 3 3 (indeed, a 1 + a 2 + a 3 = 2 + 2 + 5 = 9 a_1 + a_2 + a_3 = 2 + 2 + 5 = 9 a1+a2+a3=2+2+5=9).
In the second test case, initially, the sum of the array is 1 + 3 + 2 = 6 1+3+2 = 6 1+3+2=6, which is divisible by 3 3 3. Therefore, no moves are required. Hence, the answer is 0 0 0.
In the fourth test case, initially, the sum of the array is 1 1 1, which is not divisible by 3 3 3. By removing its only element, you will get an empty array, so its sum is 0 0 0. Hence, the answer is 1 1 1.
Solution
具体见文后视频。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
const int MAXN = 1e5 + 10;
int N;
int A[MAXN];
void solve()
{
cin >> N;
int Sum = 0, Vis[3] = {0};
for (int i = 1; i <= N; i ++)
cin >> A[i], Sum += A[i], Vis[A[i] % 3] = 1;
if (Sum % 3 == 0) cout << 0 << endl;
else if (Vis[Sum % 3]) cout << 1 << endl;
else if ((Sum + 2) / 3 * 3 - Sum == 1) cout << 1 << endl;
else cout << 2 << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
C. Turtle Fingers: Count the Values of k
Problem Statement
You are given three positive integers a a a, b b b and l l l ( a , b , l > 0 a,b,l>0 a,b,l>0).
It can be shown that there always exists a way to choose non-negative (i.e. ≥ 0 \ge 0 ≥0) integers k k k, x x x, and y y y such that l = k ⋅ a x ⋅ b y l = k \cdot a^x \cdot b^y l=k⋅ax⋅by.
Your task is to find the number of distinct possible values of k k k across all such ways.
Input
The first line contains the integer t t t ( 1 ≤ t ≤ 1 0 4 1 \le t \le 10^4 1≤t≤104) — the number of test cases.
The following t t t lines contain three integers, a a a, b b b and l l l ( 2 ≤ a , b ≤ 100 2 \le a, b \le 100 2≤a,b≤100, 1 ≤ l ≤ 1 0 6 1 \le l \le 10^6 1≤l≤106) — description of a test case.
Output
Output t t t lines, with the i i i-th ( 1 ≤ i ≤ t 1 \le i \le t 1≤i≤t) line containing an integer, the answer to the i i i-th test case.
Example
| input |
|---|
| 11 |
| 2 5 20 |
| 2 5 21 |
| 4 6 48 |
| 2 3 72 |
| 3 5 75 |
| 2 2 1024 |
| 3 7 83349 |
| 100 100 1000000 |
| 7 3 2 |
| 2 6 6 |
| 17 3 632043 |
| output |
|---|
| 6 |
| 1 |
| 5 |
| 12 |
| 6 |
| 11 |
| 24 |
| 4 |
| 1 |
| 3 |
| 24 |
Note
In the first test case, a = 2 , b = 5 , l = 20 a=2, b=5, l=20 a=2,b=5,l=20. The possible values of k k k (and corresponding x , y x,y x,y) are as follows:
- Choose k = 1 , x = 2 , y = 1 k = 1, x = 2, y = 1 k=1,x=2,y=1. Then k ⋅ a x ⋅ b y = 1 ⋅ 2 2 ⋅ 5 1 = 20 = l k \cdot a^x \cdot b^y = 1 \cdot 2^2 \cdot 5^1 = 20 = l k⋅ax⋅by=1⋅22⋅51=20=l.
- Choose k = 2 , x = 1 , y = 1 k = 2, x = 1, y = 1 k=2,x=1,y=1. Then k ⋅ a x ⋅ b y = 2 ⋅ 2 1 ⋅ 5 1 = 20 = l k \cdot a^x \cdot b^y = 2 \cdot 2^1 \cdot 5^1 = 20 = l k⋅ax⋅by=2⋅21⋅51=20=l.
- Choose k = 4 , x = 0 , y = 1 k = 4, x = 0, y = 1 k=4,x=0,y=1. Then k ⋅ a x ⋅ b y = 4 ⋅ 2 0 ⋅ 5 1 = 20 = l k \cdot a^x \cdot b^y = 4 \cdot 2^0 \cdot 5^1 = 20 = l k⋅ax⋅by=4⋅20⋅51=20=l.
- Choose k = 5 , x = 2 , y = 0 k = 5, x = 2, y = 0 k=5,x=2,y=0. Then k ⋅ a x ⋅ b y = 5 ⋅ 2 2 ⋅ 5 0 = 20 = l k \cdot a^x \cdot b^y = 5 \cdot 2^2 \cdot 5^0 = 20 = l k⋅ax⋅by=5⋅22⋅50=20=l.
- Choose k = 10 , x = 1 , y = 0 k = 10, x = 1, y = 0 k=10,x=1,y=0. Then k ⋅ a x ⋅ b y = 10 ⋅ 2 1 ⋅ 5 0 = 20 = l k \cdot a^x \cdot b^y = 10 \cdot 2^1 \cdot 5^0 = 20 = l k⋅ax⋅by=10⋅21⋅50=20=l.
- Choose k = 20 , x = 0 , y = 0 k = 20, x = 0, y = 0 k=20,x=0,y=0. Then k ⋅ a x ⋅ b y = 20 ⋅ 2 0 ⋅ 5 0 = 20 = l k \cdot a^x \cdot b^y = 20 \cdot 2^0 \cdot 5^0 = 20 = l k⋅ax⋅by=20⋅20⋅50=20=l.
In the second test case, a = 2 , b = 5 , l = 21 a=2, b=5, l=21 a=2,b=5,l=21. Note that l = 21 l = 21 l=21 is not divisible by either a = 2 a = 2 a=2 or b = 5 b = 5 b=5. Therefore, we can only set x = 0 , y = 0 x = 0, y = 0 x=0,y=0, which corresponds to k = 21 k = 21 k=21.
In the third test case, a = 4 , b = 6 , l = 48 a=4, b=6, l=48 a=4,b=6,l=48. The possible values of k k k (and corresponding x , y x,y x,y) are as follows:
- Choose k = 2 , x = 1 , y = 1 k = 2, x = 1, y = 1 k=2,x=1,y=1. Then k ⋅ a x ⋅ b y = 2 ⋅ 4 1 ⋅ 6 1 = 48 = l k \cdot a^x \cdot b^y = 2 \cdot 4^1 \cdot 6^1 = 48 = l k⋅ax⋅by=2⋅41⋅61=48=l.
- Choose k = 3 , x = 2 , y = 0 k = 3, x = 2, y = 0 k=3,x=2,y=0. Then k ⋅ a x ⋅ b y = 3 ⋅ 4 2 ⋅ 6 0 = 48 = l k \cdot a^x \cdot b^y = 3 \cdot 4^2 \cdot 6^0 = 48 = l k⋅ax⋅by=3⋅42⋅60=48=l.
- Choose k = 8 , x = 0 , y = 1 k = 8, x = 0, y = 1 k=8,x=0,y=1. Then k ⋅ a x ⋅ b y = 8 ⋅ 4 0 ⋅ 6 1 = 48 = l k \cdot a^x \cdot b^y = 8 \cdot 4^0 \cdot 6^1 = 48 = l k⋅ax⋅by=8⋅40⋅61=48=l.
- Choose k = 12 , x = 1 , y = 0 k = 12, x = 1, y = 0 k=12,x=1,y=0. Then k ⋅ a x ⋅ b y = 12 ⋅ 4 1 ⋅ 6 0 = 48 = l k \cdot a^x \cdot b^y = 12 \cdot 4^1 \cdot 6^0 = 48 = l k⋅ax⋅by=12⋅41⋅60=48=l.
- Choose k = 48 , x = 0 , y = 0 k = 48, x = 0, y = 0 k=48,x=0,y=0. Then k ⋅ a x ⋅ b y = 48 ⋅ 4 0 ⋅ 6 0 = 48 = l k \cdot a^x \cdot b^y = 48 \cdot 4^0 \cdot 6^0 = 48 = l k⋅ax⋅by=48⋅40⋅60=48=l.
Solution
具体见文后视频。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
void solve()
{
int A, B, L;
cin >> A >> B >> L;
set<int> S;
for (int a = 1; a <= L; a *= A)
for (int b = 1; b <= L; b *= B)
if (L % (a * b) == 0)
S.insert(L / (a * b));
cout << S.size() << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
D. Turtle Tenacity: Continual Mods
Problem Statement
Given an array a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an, determine whether it is possible to rearrange its elements into b 1 , b 2 , … , b n b_1, b_2, \ldots, b_n b1,b2,…,bn, such that b 1 m o d b 2 m o d … m o d b n ≠ 0 b_1 \bmod b_2 \bmod \ldots \bmod b_n \neq 0 b1modb2mod…modbn=0.
Here x m o d y x \bmod y xmody denotes the remainder from dividing x x x by y y y. Also, the modulo operations are calculated from left to right. That is, x m o d y m o d z = ( x m o d y ) m o d z x \bmod y \bmod z = (x \bmod y) \bmod z xmodymodz=(xmody)modz. For example, 2024 m o d 1000 m o d 8 = ( 2024 m o d 1000 ) m o d 8 = 24 m o d 8 = 0 2024 \bmod 1000 \bmod 8 = (2024 \bmod 1000) \bmod 8 = 24 \bmod 8 = 0 2024mod1000mod8=(2024mod1000)mod8=24mod8=0.
Input
The first line of the input contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \le t \le 10^4 1≤t≤104) — the number of test cases.
The first line of each test case contains a single integer n n n ( 2 ≤ n ≤ 1 0 5 2 \le n \le 10^5 2≤n≤105).
The second line of each test case contains n n n integers a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an ( 1 ≤ a i ≤ 1 0 9 1 \le a_i \le 10^9 1≤ai≤109).
The sum of n n n over all test cases does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.
Output
For each test case, output “YES” if it is possible, “NO” otherwise.
You can output the answer in any case (upper or lower). For example, the strings “yEs”, “yes”, “Yes”, and “YES” will be recognized as positive responses.
Example
Example
| input |
|---|
| 8 |
| 6 |
| 1 2 3 4 5 6 |
| 5 |
| 3 3 3 3 3 |
| 3 |
| 2 2 3 |
| 5 |
| 1 1 2 3 7 |
| 3 |
| 1 2 2 |
| 3 |
| 1 1 2 |
| 6 |
| 5 2 10 10 10 2 |
| 4 |
| 3 6 9 3 |
| output |
|---|
| YES |
| NO |
| YES |
| NO |
| YES |
| NO |
| YES |
| NO |
Note
In the first test case, rearranging the array into b = [ 1 , 2 , 3 , 4 , 5 , 6 ] b = [1, 2, 3, 4, 5, 6] b=[1,2,3,4,5,6] (doing nothing) would result in 1 m o d 2 m o d 3 m o d 4 m o d 5 m o d 6 = 1 1 \bmod 2 \bmod 3 \bmod 4 \bmod 5 \bmod 6 = 1 1mod2mod3mod4mod5mod6=1. Hence it is possible to achieve the goal.
In the second test case, the array b b b must be equal to [ 3 , 3 , 3 , 3 , 3 ] [3, 3, 3, 3, 3] [3,3,3,3,3], which would result in 3 m o d 3 m o d 3 m o d 3 m o d 3 = 0 3 \bmod 3 \bmod 3 \bmod 3 \bmod 3 = 0 3mod3mod3mod3mod3=0. Hence it is impossible to achieve the goal.
In the third test case, rearranging the array into b = [ 3 , 2 , 2 ] b = [3, 2, 2] b=[3,2,2] would result in 3 m o d 2 m o d 2 = 1 3 \bmod 2 \bmod 2 = 1 3mod2mod2=1. Hence it is possible to achieve the goal.
Solution
具体见文后视频。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
const int MAXN = 2e5 + 10;
int N;
int A[MAXN];
void solve()
{
unordered_map<int, int> Cnt;
cin >> N;
for (int i = 1; i <= N; i ++)
cin >> A[i], Cnt[A[i]] ++;
sort(A + 1, A + 1 + N);
if (Cnt[A[1]] == 1) cout << "YES" << endl;
else
{
int mn = 1e18;
for (int i = 1; i <= N; i ++)
if (A[i] % A[1] != 0)
mn = min(mn, A[i] % A[1]);
if (mn == 1e18) cout << "NO" << endl;
else cout << "YES" << endl;
}
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
E. Turtle vs. Rabbit Race: Optimal Trainings
Problem Statement
Isaac begins his training. There are n n n running tracks available, and the i i i-th track ( 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n) consists of a i a_i ai equal-length sections.
Given an integer u u u ( 1 ≤ u ≤ 1 0 9 1 \le u \le 10^9 1≤u≤109), finishing each section can increase Isaac’s ability by a certain value, described as follows:
- Finishing the 1 1 1-st section increases Isaac’s performance by u u u.
- Finishing the 2 2 2-nd section increases Isaac’s performance by u − 1 u-1 u−1.
- Finishing the 3 3 3-rd section increases Isaac’s performance by u − 2 u-2 u−2.
- … \ldots …
- Finishing the k k k-th section ( k ≥ 1 k \ge 1 k≥1) increases Isaac’s performance by u + 1 − k u+1-k u+1−k. (The value u + 1 − k u+1-k u+1−k can be negative, which means finishing an extra section decreases Isaac’s performance.)
You are also given an integer l l l. You must choose an integer r r r such that l ≤ r ≤ n l \le r \le n l≤r≤n and Isaac will finish each section of each track l , l + 1 , … , r l, l + 1, \dots, r l,l+1,…,r (that is, a total of ∑ i = l r a i = a l + a l + 1 + … + a r \sum_{i=l}^r a_i = a_l + a_{l+1} + \ldots + a_r ∑i=lrai=al+al+1+…+ar sections).
Answer the following question: what is the optimal r r r you can choose that the increase in Isaac’s performance is maximum possible?
If there are multiple r r r that maximize the increase in Isaac’s performance, output the smallest r r r.
To increase the difficulty, you need to answer the question for q q q different values of l l l and u u u.
Input
The first line of input contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \le t \le 10^4 1≤t≤104) — the number of test cases.
The descriptions of the test cases follow.
The first line contains a single integer n n n ( 1 ≤ n ≤ 1 0 5 1 \le n \le 10^5 1≤n≤105).
The second line contains n n n integers a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an ( 1 ≤ a i ≤ 1 0 4 1 \le a_i \le 10^4 1≤ai≤104).
The third line contains a single integer q q q ( 1 ≤ q ≤ 1 0 5 1 \le q \le 10^5 1≤q≤105).
The next q q q lines each contain two integers l l l and u u u ( 1 ≤ l ≤ n , 1 ≤ u ≤ 1 0 9 1 \le l \le n, 1 \le u \le 10^9 1≤l≤n,1≤u≤109) — the descriptions to each query.
The sum of n n n over all test cases does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105. The sum of q q q over all test cases does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.
Output
For each test case, output q q q integers: the i i i-th integer contains the optimal r r r for the i i i-th query. If there are multiple solutions, output the smallest one.
Example
| input |
|---|
| 5 |
| 6 |
| 3 1 4 1 5 9 |
| 3 |
| 1 8 |
| 2 7 |
| 5 9 |
| 1 |
| 10 |
| 1 |
| 1 1 |
| 9 |
| 5 10 9 6 8 3 10 7 3 |
| 5 |
| 8 56 |
| 1 12 |
| 9 3 |
| 1 27 |
| 5 45 |
| 5 |
| 7 9 2 5 2 |
| 10 |
| 1 37 |
| 2 9 |
| 3 33 |
| 4 32 |
| 4 15 |
| 2 2 |
| 4 2 |
| 2 19 |
| 3 7 |
| 2 7 |
| 10 |
| 9 1 6 7 6 3 10 7 3 10 |
| 5 |
| 10 43 |
| 3 23 |
| 9 3 |
| 6 8 |
| 5 14 |
| output |
|---|
| 3 4 5 |
| 1 |
| 9 2 9 4 9 |
| 5 2 5 5 5 2 4 5 4 2 |
| 10 6 9 7 7 |
Note
For the 1 1 1-st query in the first test case:
- By choosing r = 3 r = 3 r=3, Isaac finishes a 1 + a 2 + a 3 = 3 + 1 + 4 = 8 a_1 + a_2 + a_3 = 3 + 1 + 4 = 8 a1+a2+a3=3+1+4=8 sections in total, hence his increase in performance is u + ( u − 1 ) + … + ( u − 7 ) = 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36 u+(u-1)+\ldots+(u-7)=8+7+6+5+4+3+2+1 = 36 u+(u−1)+…+(u−7)=8+7+6+5+4+3+2+1=36.
- By choosing r = 4 r = 4 r=4, Isaac finishes a 1 + a 2 + a 3 + a 4 = 3 + 1 + 4 + 1 = 9 a_1 + a_2 + a_3 + a_4 = 3 + 1 + 4 + 1 = 9 a1+a2+a3+a4=3+1+4+1=9 sections in total, hence his increase in performance is u + ( u − 1 ) + … + ( u − 8 ) = 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 36 u+(u-1)+\ldots+(u-8)=8+7+6+5+4+3+2+1+0 = 36 u+(u−1)+…+(u−8)=8+7+6+5+4+3+2+1+0=36.
Both choices yield the optimal increase in performance, however we want to choose the smallest r r r. So we choose r = 3 r = 3 r=3.
For the 2 2 2-nd query in the first test case, by choosing r = 4 r = 4 r=4, Isaac finishes a 2 + a 3 + a 4 = 1 + 4 + 1 = 6 a_2 + a_3 + a_4 = 1 + 4 + 1 = 6 a2+a3+a4=1+4+1=6 sections in total, hence his increase in performance is u + ( u − 1 ) + … + ( u − 5 ) = 7 + 6 + 5 + 4 + 3 + 2 = 27 u+(u-1)+\ldots+(u-5)=7+6+5+4+3+2 = 27 u+(u−1)+…+(u−5)=7+6+5+4+3+2=27. This is the optimal increase in performance.
For the 3 3 3-rd query in the first test case:
- By choosing r = 5 r = 5 r=5, Isaac finishes a 5 = 5 a_5 = 5 a5=5 sections in total, hence his increase in performance is u + ( u − 1 ) + … + ( u − 4 ) = 9 + 8 + 7 + 6 + 5 = 35 u+(u-1)+\ldots+(u-4)=9+8+7+6+5 = 35 u+(u−1)+…+(u−4)=9+8+7+6+5=35.
- By choosing r = 6 r = 6 r=6, Isaac finishes a 5 + a 6 = 5 + 9 = 14 a_5 + a_6 = 5 + 9 = 14 a5+a6=5+9=14 sections in total, hence his increase in performance is u + ( u − 1 ) + … + ( u − 13 ) = 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + ( − 1 ) + ( − 2 ) + ( − 3 ) + ( − 4 ) = 35 u+(u-1)+\ldots+(u-13)=9+8+7+6+5+4+3+2+1+0+(-1)+(-2)+(-3)+(-4) = 35 u+(u−1)+…+(u−13)=9+8+7+6+5+4+3+2+1+0+(−1)+(−2)+(−3)+(−4)=35.
Both choices yield the optimal increase in performance, however we want to choose the smallest r r r. So we choose r = 5 r = 5 r=5.
Hence the output for the first test case is [ 3 , 4 , 5 ] [3, 4, 5] [3,4,5].
Solution
具体见文后视频。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
const int MAXN = 2e5 + 10;
int N, Q;
int A[MAXN];
int F(int l, int r, int u)
{
int Section = A[r] - A[l - 1];
return (2 * u + 1 - Section) * Section / 2;
}
void solve()
{
cin >> N;
for (int i = 1; i <= N; i ++)
cin >> A[i], A[i] += A[i - 1];
cin >> Q;
while (Q --)
{
int L, U;
cin >> L >> U;
int l = L, r = N;
while(l < r) {
int lmid = l + (r - l) / 3;
int rmid = r - (r - l) / 3;
if(F(L, lmid, U) < F(L, rmid, U)) l = lmid + 1;
else r = rmid - 1;
}
cout << l << " ";
}
cout << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
F. Turtle Mission: Robot and the Earthquake
Problem Statement
The world is a grid with n n n rows and m m m columns. The rows are numbered 0 , 1 , … , n − 1 0, 1, \ldots, n-1 0,1,…,n−1, while the columns are numbered 0 , 1 , … , m − 1 0, 1, \ldots, m-1 0,1,…,m−1. In this world, the columns are cyclic (i.e. the top and the bottom cells in each column are adjacent). The cell on the i i i-th row and the j j j-th column ( 0 ≤ i < n , 0 ≤ j < m 0 \le i < n, 0 \le j < m 0≤i<n,0≤j<m) is denoted as ( i , j ) (i,j) (i,j).
At time 0 0 0, the cell ( i , j ) (i,j) (i,j) (where 0 ≤ i < n , 0 ≤ j < m 0 \le i < n, 0 \le j < m 0≤i<n,0≤j<m) contains either a rock or nothing. The state of cell ( i , j ) (i,j) (i,j) can be described using the integer a i , j a_{i,j} ai,j:
- If a i , j = 1 a_{i,j} = 1 ai,j=1, there is a rock at ( i , j ) (i,j) (i,j).
- If a i , j = 0 a_{i,j} = 0 ai,j=0, there is nothing at ( i , j ) (i,j) (i,j).
As a result of aftershocks from the earthquake, the columns follow tectonic plate movements: each column moves cyclically upwards at a velocity of 1 1 1 cell per unit of time. Formally, for some 0 ≤ i < n , 0 ≤ j < m 0 \le i < n, 0 \le j < m 0≤i<n,0≤j<m, if ( i , j ) (i,j) (i,j) contains a rock at the moment, it will move from ( i , j ) (i, j) (i,j) to ( i − 1 , j ) (i - 1, j) (i−1,j) (or to ( n − 1 , j ) (n - 1, j) (n−1,j) if i = 0 i=0 i=0).
The robot called RT is initially positioned at ( 0 , 0 ) (0,0) (0,0). It has to go to ( n − 1 , m − 1 ) (n-1,m-1) (n−1,m−1) to carry out an earthquake rescue operation (to the bottom rightmost cell). The earthquake doesn’t change the position of the robot, they only change the position of rocks in the world.
Let RT’s current position be ( x , y ) (x,y) (x,y) ( 0 ≤ x < n , 0 ≤ y < m 0 \le x < n, 0 \le y < m 0≤x<n,0≤y<m), it can perform the following operations:
- Go one cell cyclically upwards, i.e. from ( x , y ) (x,y) (x,y) to ( ( x + n − 1 ) m o d n , y ) ((x+n-1) \bmod n, y) ((x+n−1)modn,y) using 1 1 1 unit of time.
- Go one cell cyclically downwards, i.e. ( x , y ) (x,y) (x,y) to ( ( x + 1 ) m o d n , y ) ((x+1) \bmod n, y) ((x+1)modn,y) using 1 1 1 unit of time.
- Go one cell to the right, i.e. ( x , y ) (x,y) (x,y) to ( x , y + 1 ) (x, y+1) (x,y+1) using 1 1 1 unit of time. (RT may perform this operation only if y < m − 1 y < m-1 y<m−1.)
Note that RT cannot go left using the operations nor can he stay at a position.
Unfortunately, RT will explode upon colliding with a rock. As such, when RT is at ( x , y ) (x,y) (x,y) and there is a rock at ( ( x + 1 ) m o d n , y ) ((x+1) \bmod n, y) ((x+1)modn,y) or ( ( x + 2 ) m o d n , y ) ((x+2) \bmod n, y) ((x+2)modn,y), RT cannot move down or it will be hit by the rock.
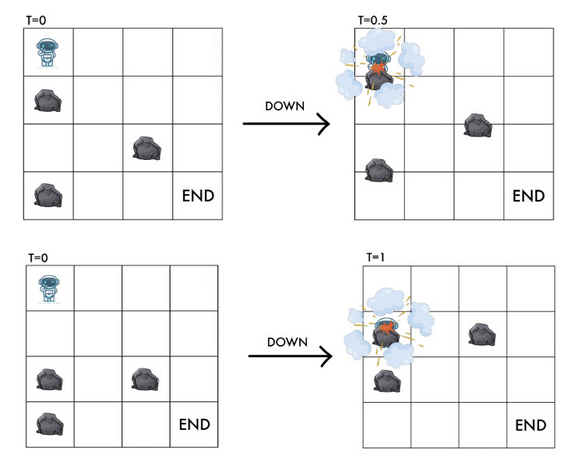
Similarly, if y + 1 < m y+1 < m y+1<m and there is a rock at ( ( x + 1 ) m o d n , y + 1 ) ((x+1) \bmod n, y+1) ((x+1)modn,y+1), RT cannot move right or it will be hit by the rock.
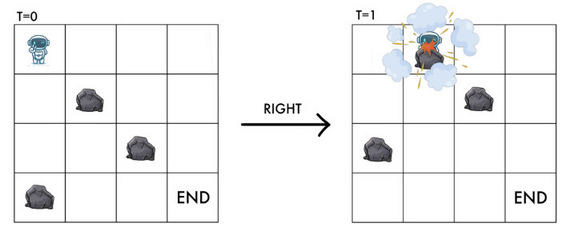
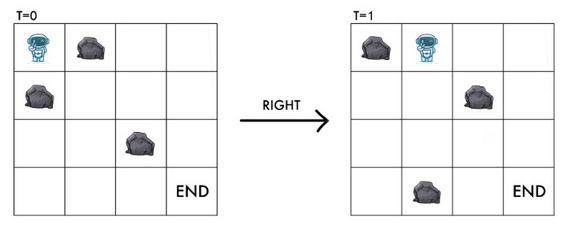
However, it is worth noting that if there is a rock at ( x m o d n , y + 1 ) (x \bmod n, y+1) (xmodn,y+1) and ( ( x + 1 ) m o d n , y ) ((x+1) \bmod n, y) ((x+1)modn,y), RT can still move right safely.
Find the minimum amount of time RT needs to reach ( n − 1 , m − 1 ) (n-1,m-1) (n−1,m−1) without colliding with any rocks. If it is impossible to do so, output − 1 -1 −1.
Input
The first line of the input contains one integer t t t ( 1 ≤ t ≤ 1 0 4 1 \le t \le 10^4 1≤t≤104) — the number of test cases.
In each test case, the first line contains two integers n n n, m m m ( 3 ≤ n , m ≤ 1 0 3 3 \le n, m \le 10^3 3≤n,m≤103) — the size of the planet’s boundaries.
Each of the next n n n lines contains m m m integers. The ( j + 1 ) (j+1) (j+1)-th integer on the ( i + 1 ) (i+1) (i+1)-th line ( 0 ≤ i < n , 0 ≤ j < m 0 \le i < n, 0 \le j < m 0≤i<n,0≤j<m) is a i , j a_{i,j} ai,j ( 0 ≤ a i , j ≤ 1 0 \le a_{i,j} \le 1 0≤ai,j≤1), which denotes whether or not there is a rock at ( i , j ) (i,j) (i,j) at time 0 0 0.
Additionally, it is guaranteed that a 0 , 0 = 0 a_{0,0} = 0 a0,0=0, and a i , m − 1 = 0 a_{i, m-1} = 0 ai,m−1=0 for 0 ≤ i < n 0 \le i < n 0≤i<n. In other words, there is no rock at RT’s initial position as well as column m − 1 m-1 m−1.
The sum of n ⋅ m n \cdot m n⋅m over all test cases does not exceed 1 0 6 10^6 106.
Output
For each test case:
- If the destination can be reached without colliding with any rocks, output a single integer — the minimum amount of time RT needs to reach ( n − 1 , m − 1 ) (n-1,m-1) (n−1,m−1).
- Otherwise, output − 1 -1 −1.
Example
| input |
|---|
| 6 |
| 4 5 |
| 0 1 0 0 0 |
| 0 0 1 0 0 |
| 1 0 1 1 0 |
| 0 0 0 0 0 |
| 3 3 |
| 0 0 0 |
| 1 0 0 |
| 0 0 0 |
| 5 3 |
| 0 0 0 |
| 0 0 0 |
| 1 0 0 |
| 0 0 0 |
| 1 0 0 |
| 3 7 |
| 0 0 1 0 0 1 0 |
| 1 0 1 0 1 0 0 |
| 0 1 0 0 0 0 0 |
| 3 4 |
| 0 1 0 0 |
| 1 0 0 0 |
| 0 1 1 0 |
| 5 5 |
| 0 0 0 0 0 |
| 0 1 0 1 0 |
| 0 1 0 1 0 |
| 0 1 0 1 0 |
| 0 0 0 1 0 |
| output |
|---|
| 7 |
| 3 |
| 3 |
| 8 |
| -1 |
| 12 |
| input |
|---|
| 6 |
| 3 3 |
| 0 0 0 |
| 0 0 0 |
| 0 0 0 |
| 4 3 |
| 0 1 0 |
| 1 0 0 |
| 0 1 0 |
| 1 0 0 |
| 4 3 |
| 0 1 0 |
| 0 1 0 |
| 0 1 0 |
| 0 1 0 |
| 3 3 |
| 0 0 0 |
| 1 1 0 |
| 0 0 0 |
| 3 3 |
| 0 1 0 |
| 0 0 0 |
| 0 1 0 |
| 5 5 |
| 0 0 0 0 0 |
| 0 1 1 0 0 |
| 0 1 1 0 0 |
| 0 0 0 0 0 |
| 0 0 1 0 0 |
| output |
|---|
| 3 |
| 3 |
| -1 |
| -1 |
| 3 |
| 8 |
Note
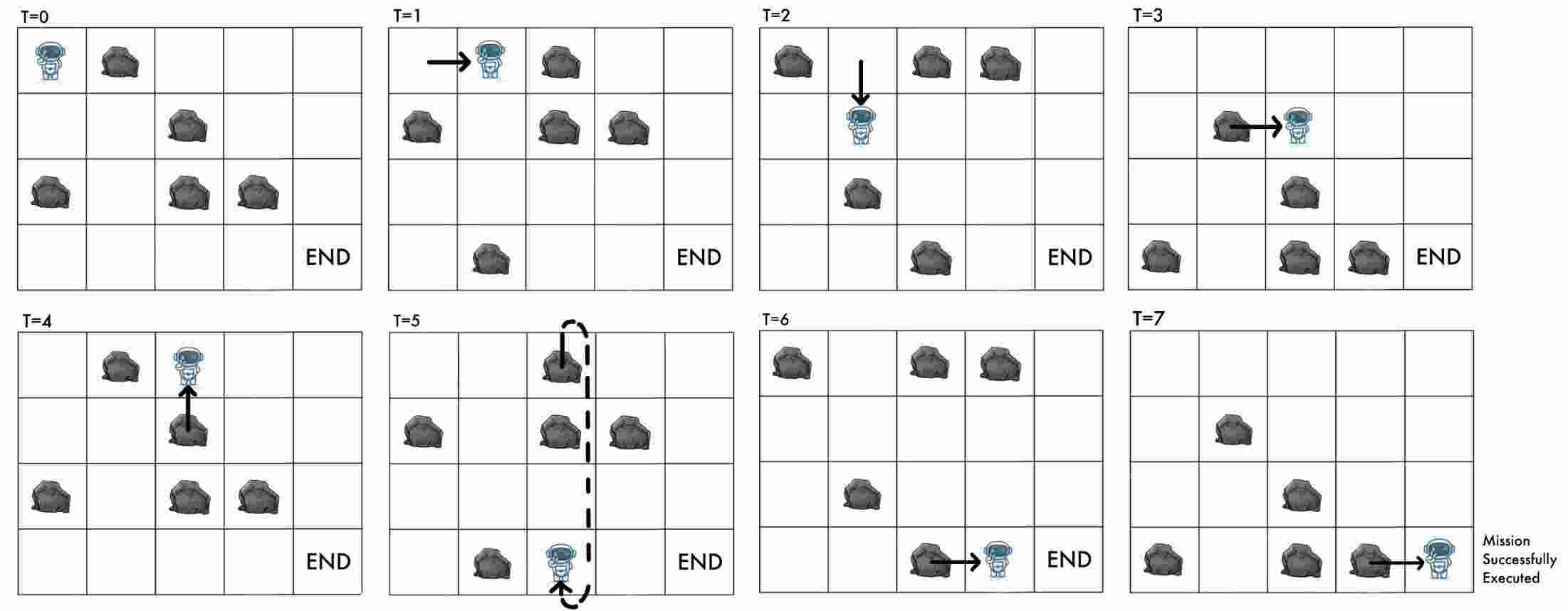
Visual explanation of the first test case in the example:
Solution
具体见文后视频。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
const int MAXN = 1e3 + 10;
int N, M;
int Gr[MAXN][MAXN];
int dist[MAXN][MAXN], Vis[MAXN][MAXN];
void solve()
{
cin >> N >> M;
for (int i = 0; i < N; i ++)
for (int j = 0; j < M; j ++)
cin >> Gr[i][j];
for (int i = 0; i < N; i ++)
for (int j = 0; j < M; j ++)
dist[i][j] = -1;
queue<PII> Q;
Q.emplace(0, 0), dist[0][0] = 0;
while (Q.size())
{
auto P = Q.front();
Q.pop();
int x = P.first, y = P.second;
if (!Gr[(x + 2) % N][y] && !Gr[(x + 1) % N][y] && dist[(x + 2) % N][y] == -1)
{
dist[(x + 2) % N][y] = dist[x][y] + 1;
Q.emplace((x + 2) % N, y);
}
if (y + 1 < M && !Gr[(x + 1) % N][y + 1] && dist[(x + 1) % N][y + 1] == -1)
{
dist[(x + 1) % N][y + 1] = dist[x][y] + 1;
Q.emplace((x + 1) % N, y + 1);
}
}
int res = 1e18;
for (int i = 0; i < N; i ++)
{
if (dist[i][M - 1] == -1) continue;
int finish = (N - 1 + dist[i][M - 1]) % N;
res = min(res, dist[i][M - 1] + min((finish - i + N) % N, (i - finish + N) % N));
}
if (res == 1e18) cout << -1 << endl;
else cout << res << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
G. Turtle Magic: Royal Turtle Shell Pattern
Problem Statement
Turtle Alice is currently designing a fortune cookie box, and she would like to incorporate the theory of LuoShu into it.
The box can be seen as an n × m n \times m n×m grid ( n , m ≥ 5 n, m \ge 5 n,m≥5), where the rows are numbered 1 , 2 , … , n 1, 2, \dots, n 1,2,…,n and columns are numbered 1 , 2 , … , m 1, 2, \dots, m 1,2,…,m. Each cell can either be empty or have a single fortune cookie of one of the following shapes: circle or square. The cell at the intersection of the a a a-th row and the b b b-th column is denoted as ( a , b ) (a, b) (a,b).
Initially, the entire grid is empty. Then, Alice performs q q q operations on the fortune cookie box. The i i i-th operation ( 1 ≤ i ≤ q 1 \le i \le q 1≤i≤q) is as follows: specify a currently empty cell ( r i , c i ) (r_i,c_i) (ri,ci) and a shape (circle or square), then put a fortune cookie of the specified shape on cell ( r i , c i ) (r_i,c_i) (ri,ci). Note that after the i i i-th operation, the cell ( r i , c i ) (r_i,c_i) (ri,ci) is no longer empty.
Before all operations and after each of the q q q operations, Alice wonders what the number of ways to place fortune cookies in all remaining empty cells is, such that the following condition is satisfied:
No three consecutive cells (in horizontal, vertical, and both diagonal directions) contain cookies of the same shape. Formally:
- There does not exist any ( i , j ) (i,j) (i,j) satisfying 1 ≤ i ≤ n , 1 ≤ j ≤ m − 2 1 \le i \le n, 1 \le j \le m-2 1≤i≤n,1≤j≤m−2, such that there are cookies of the same shape in cells ( i , j ) , ( i , j + 1 ) , ( i , j + 2 ) (i,j), (i,j+1), (i,j+2) (i,j),(i,j+1),(i,j+2).
- There does not exist any ( i , j ) (i,j) (i,j) satisfying 1 ≤ i ≤ n − 2 , 1 ≤ j ≤ m 1 \le i \le n-2, 1 \le j \le m 1≤i≤n−2,1≤j≤m, such that there are cookies of the same shape in cells ( i , j ) , ( i + 1 , j ) , ( i + 2 , j ) (i,j), (i+1,j), (i+2,j) (i,j),(i+1,j),(i+2,j).
- There does not exist any ( i , j ) (i,j) (i,j) satisfying 1 ≤ i ≤ n − 2 , 1 ≤ j ≤ m − 2 1 \le i \le n-2, 1 \le j \le m-2 1≤i≤n−2,1≤j≤m−2, such that there are cookies of the same shape in cells ( i , j ) , ( i + 1 , j + 1 ) , ( i + 2 , j + 2 ) (i,j), (i+1,j+1), (i+2,j+2) (i,j),(i+1,j+1),(i+2,j+2).
- There does not exist any ( i , j ) (i,j) (i,j) satisfying 1 ≤ i ≤ n − 2 , 1 ≤ j ≤ m − 2 1 \le i \le n-2, 1 \le j \le m-2 1≤i≤n−2,1≤j≤m−2, such that there are cookies of the same shape in cells ( i , j + 2 ) , ( i + 1 , j + 1 ) , ( i + 2 , j ) (i,j+2), (i+1,j+1), (i+2,j) (i,j+2),(i+1,j+1),(i+2,j).
You should output all answers modulo 998 244 353 998\,244\,353 998244353. Also note that it is possible that after some operations, the condition is already not satisfied with the already placed candies, in this case you should output 0 0 0.
Input
The first line of the input contains a single integer t t t ( 1 ≤ t ≤ 1 0 3 1 \le t \le 10^3 1≤t≤103) — the number of test cases.
The first line of each test case contains three integers n n n, m m m, q q q ( 5 ≤ n , m ≤ 1 0 9 , 0 ≤ q ≤ min ( n × m , 1 0 5 ) 5 \le n, m \le 10^9, 0 \le q \le \min(n \times m, 10^5) 5≤n,m≤109,0≤q≤min(n×m,105)).
The i i i-th of the next q q q lines contains two integers r i r_i ri, c i c_i ci and a single string shape i \text{shape}_i shapei ( 1 ≤ r i ≤ n , 1 ≤ c i ≤ m 1 \le r_i \le n, 1 \le c_i \le m 1≤ri≤n,1≤ci≤m, shape i = \text{shape}_i= shapei= “circle” or “square”), representing the operations. It is guaranteed that the cell on the r i r_i ri-th row and the c i c_i ci-th column is initially empty. That means, each ( r i , c i ) (r_i,c_i) (ri,ci) will appear at most once in the updates.
The sum of q q q over all test cases does not exceed 1 0 5 10^5 105.
Output
For each test case, output q + 1 q+1 q+1 lines. The first line of each test case should contain the answer before any operations. The i i i-th line ( 2 ≤ i ≤ q + 1 2 \le i \le q+1 2≤i≤q+1) should contain the answer after the first i − 1 i-1 i−1 operations. All answers should be taken modulo 998 244 353 998\,244\,353 998244353.
Example
| input |
|---|
| 2 |
| 6 7 4 |
| 3 3 circle |
| 3 6 square |
| 5 3 circle |
| 5 4 square |
| 5 5 3 |
| 1 1 circle |
| 1 2 circle |
| 1 3 circle |
| output |
|---|
| 8 |
| 4 |
| 3 |
| 1 |
| 0 |
| 8 |
| 4 |
| 1 |
| 0 |
Note
In the second sample, after placing a circle-shaped fortune cookie to cells ( 1 , 1 ) (1,1) (1,1), ( 1 , 2 ) (1,2) (1,2) and ( 1 , 3 ) (1,3) (1,3), the condition is already not satisfied. Therefore, you should output 0 0 0.
Solution
具体见文后视频。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
int get(int x, int y, int i)
{
if (i >= 4) return get(y, x, i - 4);
y += i;
return (x & 1) ^ ((y % 4 <= 2) && (y % 4 >= 1));
}
void solve()
{
int n, m, q;
cin >> n >> m >> q;
int res = 8, flg[8] = {0};
cout << res << endl;
while (q --)
{
int x, y;
string s;
cin >> x >> y >> s;
int v = s[0] == 'c';
for (int i = 0; i < 8; i ++)
if (!flg[i] && get(x, y, i) != v)
res --, flg[i] = 1;
cout << res << endl;
}
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
视频讲解
Codeforces Round 929 (Div. 3)(A ~ G 题讲解)
最后祝大家早日