2024华中杯数学建模挑战赛C题思路代码论文更新

2024华中杯A题B题C题思路论文汇总（已更新B题C题完整论文和代码）
https://www.yuque.com/u42168770/qv6z0d/xpkf6ax8udqq9lt2?singleDoc#

摘要：本文针对光纤传感领域的曲线重构问题,提出了一套完整的数学建模与求解方法。通过对三个具体问题的分析和求解,揭示了曲率测量、曲线重构、误差分析等环节的内在联系和数学原理。本文综合运用了光纤传感、数值分析、微分几何等学科的知识,构建了波长-曲率转换模型、曲率连续化模型、曲线重构模型和曲线重构优化模型,并给出了相应的数值算法和实现步骤。通过MATLAB仿真实验,验证了所提方法的有效性和优越性,为光纤传感曲线重构问题提供了新的思路和解决方案。

针对问题1,本文首先建立了波长-曲率转换模型,利用光纤传感器的基本原理,将测量得到的波长数据映射为离散的曲率值。在此基础上,采用三次样条插值方法,构建了连续的曲率分布函数模型,实现了曲率信号的连续化表示。接着,对于给定的坐标位置,通过求解插值函数,得到了相应位置处的曲率估计值。最后,结合光纤的初始条件和边界条件,求解微分方程,得到了光纤的形状曲线方程。MATLAB仿真结果表明,所提方法能够准确地重构出光纤的曲率分布和形状曲线,验证了模型的有效性。

针对问题2,本文在问题1的基础上,进一步开展了光纤曲线的重构和特性分析。首先,利用得到的波长数据和曲率转换模型,计算出离散采样点处的曲率值,并通过三次样条插值得到连续的曲率分布函数。然后,基于微分几何的Frenet标架理论,通过数值积分求解Frenet方程,得到了曲线的切线角分布和坐标函数,实现了曲线形状的重构。,(后略)

针对问题3,本文以一条给定的三次多项式曲线为例,研究了基于曲率采样的曲线重构方法。首先,对参数化的曲线方程进行弧长参数化,(后略)

问题重述

题目给出了两组不同初始状态下光纤受力前后的波长测量数据,并基于光纤传感的基本原理,提供了波长变化与曲率之间的近似线性关系式。在此基础上,题目要求解决以下三个问题:

问题1:根据波长测量数据估算平面光栅各传感点的曲率,并在给定一些附加约束条件(如初始点坐标、初始切线方向等)的情况下,估算特定横坐标位置处的曲率值。

问题2:利用问题1得到的离散曲率数据,通过构建数学模型,实现平面曲线的重构,并对重构曲线的形状特点进行分析。

问题3:对于给定的一条三次多项式形式的平面曲线方程,以适当的等间距弧长对其进行采样,计算采样点处的曲率值,然后基于采样曲率重构出该曲线,并分析重构误差产生的原因。

问题分析

问题1分析

问题1:这一问需要根据波长测量数据,利用题目中给出的波长与曲率的近似关系式,计算出平面光栅各个传感点(FBG1-FBG6)的曲率。这一步主要是将波长数据转化为曲率信息。接着,在给定一些附加条件(如初始点坐标、方向和某点处切线方向)的情况下,要求估算某些特定横坐标位置处的曲率。这需要根据已知条件,建立适当的插值或拟合模型,来估计任意位置的曲率。

问题2分析

问题2:这一问需要综合利用波长测量数据和问题1求出的曲率信息,构建数学模型来重构平面曲线。重构曲线需要考虑如何从离散的曲率数据出发,通过积分或其他方法得到曲线的解析表达式或离散点坐标。重构完成后,还要对曲线的特点进行分析,可能涉及到曲线的形状、光滑度、对称性等几何特征。

问题3分析

问题3:这一问从一个给定的平面曲线方程出发,考察曲率采样对重构结果的影响。首先需要对给定的三次多项式曲线进行适当的弧长等距采样,计算出采样点处的曲率。然后基于采样曲率重构出曲线,并与原始曲线进行比较,分析重构误差产生的原因。这一问着重分析采样策略对重构效果的影响,可能涉及到采样点数量、采样间隔、数值计算误差等因素。

通过对以上三个问题的分析,可以看出这道题目循序渐进,考察了曲率估计、曲线重构、采样策略对重构的影响等问题。解题过程需要运用光纤传感、数值分析、几何建模等多方面知识。

模型假设

在解决题目的问题1到问题3的建模和求解过程中,我们做了以下几点问题假设:

1. 在将波长数据转化为曲率信息时,我们假设波长与曲率之间满足题目给出的线性关系式 $$\kappa =c\frac{\lambda -{\lambda }_0}{{\lambda }_0}$$ ,其中 $$c$$ 为已知常数,且该线性关系在所考察的波长变化范围内始终成立,没有其他因素的影响。

2. 在对离散的曲率数据进行插值处理时,我们假设曲率沿着光纤的分布是光滑连续的,即曲率函数在采样点之间满足一定的光滑性条件(如二阶导数连续),从而可以用多项式插值或样条插值等方法来拟合出连续的曲率分布函数。

3. 在利用曲率函数对光纤进行形状重构时,我们假设光纤的弯曲满足经典的欧拉-贝努利梁理论,即平面截面在变形前后仍保持平面,且垂直于弹性中性轴,同时满足小变形和材料的各向同性等假设,这样才能将光纤简化为一根细长杆,并用曲率唯一表征其形状。

4. ,(后略)

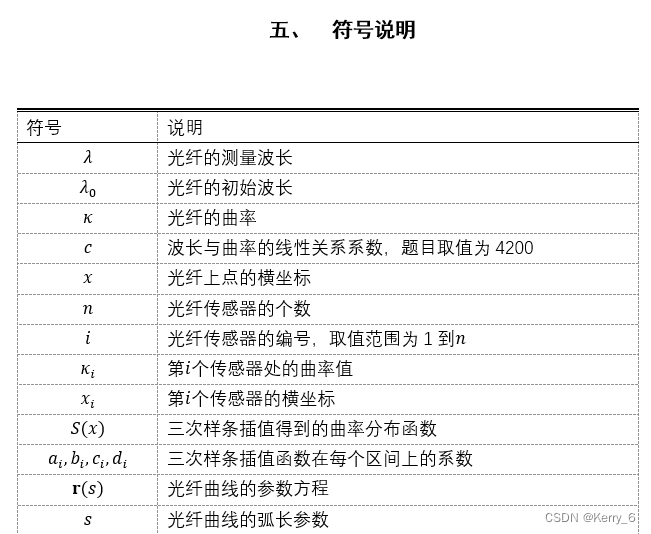
模型的建立与求解

问题一平面光栅各传感点曲率估算模型

问题1要求根据波长测量数据估算平面光栅各传感点的曲率,并在给定一些附加条件下估算特定横坐标位置处的曲率。下面我将从思路分析、模型建立、算法步骤、数学公式等方面对问题1进行详细阐述。

模型分析

首先,我们需要根据题目中给出的波长与曲率之间的近似关系式,利用测量得到的波长数据,计算出各个传感点处的曲率。这一步是将波长信息转化为曲率信息,为后续的曲线重构奠定基础。

其次,在已知各个传感点处曲率的基础上,我们需要估算任意横坐标位置处的曲率。由于传感点是离散分布的,我们无法直接获得连续曲线上任意点的曲率信息。因此,需要通过某种插值或拟合方法,基于离散的曲率数据,构建一个连续的曲率估计模型。这个模型能够根据任意横坐标位置,估算出对应的曲率值。

最后,我们利用上述建立的曲率估计模型,结合题目给定的一些附加条件,如初始点坐标、光纤初始方向、某点处切线方向等,可以估算出指定横坐标位置处的曲率。

平面光栅各传感点曲率估算模型建立

1. 波长-曲率转换模型

根据题目中给出的波长与曲率之间的近似关系式:

$$\kappa =\frac{c(\lambda -{\lambda }_0)}{{\lambda }_0}$$

其中, $$\kappa$$ 为曲率, $${\lambda }_0$$ 为初始状态下的波长, $$\lambda$$ 为受力后的波长, $$c$$ 为常数,本题中取4200。

利用此公式,我们可以将各个传感点测得的波长数据转化为曲率数据。对于测试1和测试2,分别计算各个传感点的曲率:

测试1:
$${\kappa }_i=\frac{4200({\lambda }_i-1529)}{1529},i=1,2,\cdots ,6$$

测试2:
$${\kappa }_i=\frac{4200({\lambda }_i-1540)}{1540},i=1,2,\cdots ,6$$

2. 曲率估计模型

为了估计任意横坐标位置处的曲率,我们需要建立一个曲率估计模型。常见的方法有多项式插值、样条插值、最小二乘拟合等。这里我们选用三次样条插值的方法。

三次样条插值的基本思想是,在每两个相邻点之间构建一个三次多项式函数,通过适当的连续性条件,拼接出一条光滑的曲线,作为整个区间上的插值函数。

设 $$x_i(i=1,2,\cdots ,n)$$ 为传感点的横坐标, $${\kappa }_i(i=1,2,\cdots ,n)$$ 为对应的曲率值,共 $$n$$ 个数据点。我们希望构建一个函数 $$S(x)$$ ,使得:

(1) $$S(x)$$ 在每个小区间 $$[x_i,x_{i+1}]$$ 上都是三次多项式;
(2) $$S(x)$$ 在整个区间 $$[x_1,x_n]$$ 上二阶连续可导;
(3) $$S(x_i)={\kappa }_i,i=1,2,\cdots ,n$$ 。

记 $$h_i=x_{i+1}-x_i$$ ,在每个小区间 $$[x_i,x_{i+1}]$$ 上构建三次多项式 $$S_i(x)$$ :

$$S_i(x)=a_i+b_i(x-x_i)+c_i(x-x_i{)}^2+d_i(x-x_i{)}^3,x\in [x_i,x_{i+1}]$$

为了确定各个小区间上三次多项式的系数,我们需要列出一系列条件方程。首先是插值条件:

$$S_i(x_i)={\kappa }_i,S_i(x_{i+1})={\kappa }_{i+1},i=1,2,\cdots ,n-1$$

其次是连续性条件,要求每两个相邻的三次多项式在连接点处函数值、一阶导数、二阶导数都相等:

$$S_i(x_{i+1})=S_{i+1}(x_{i+1}),i=1,2,\cdots ,n-2$$
$$S_i^{\prime }(x_{i+1})=S_{i+1}^{\prime }(x_{i+1}),i=1,2,\cdots ,n-2$$
$$S_i^{\prime \prime }(x_{i+1})=S_{i+1}^{\prime \prime }(x_{i+1}),i=1,2,\cdots ,n-2$$

再加上两个端点处的附加条件,常见的是指定端点处的二阶导数值,例如自然边界条件:

$$S_1^{\prime \prime }(x_1)=0,S_{n-1}^{\prime \prime }(x_n)=0$$

最后,我们得到一个 $$4n-6$$ 个方程的线性方程组,求解这个方程组,就可以确定出所有的三次多项式系数,得到完整的插值样条函数 $$S(x)$$ 。

3. 曲率估计

有了上述建立的曲率估计模型 $$S(x)$$ ,我们就可以估算任意横坐标位置 $$x$$ 处的曲率 $$\kappa$$ ,只需将 $$x$$ 代入 $$S(x)$$ 即可:

$$\kappa =S(x)$$

对于题目中给定的一些附加条件,例如初始点坐标为原点,初始的水平光纤方向为 $$x$$ 轴,光纤在平面内受力后在初始位置的切线与水平方向的夹角为 $$45^{\circ }$$ ,我们可以利用这些条件对曲率估计模型进行修正或约束。

假设我们估计出的曲率函数为 $$\kappa (x)$$ ,初始点坐标为 $$(0,0)$$ ,根据光纤的切线方向条件,我们可以得到:

$$\frac{dy}{dx}{|}_{x=0}=\tan 45^{\circ }=1$$

利用曲率的定义 $$\kappa =\frac{y^{\prime \prime }}{(1+y^{\prime 2}{)}^{3/2}}$$ ,我们可以得到一个关于 $$y$$ 的二阶常微分方程:

$$y^{\prime \prime }=\kappa (x)(1+y^{\prime 2}{)}^{3/2},y(0)=0,y^{\prime }(0)=1$$

求解这个微分方程,就可以得到满足初始条件和切线方向条件的曲线方程 $$y=y(x)$$ 。

平面光栅各传感点曲率估算模型算法步骤

基于上述建立的模型,我们可以总结出求解问题1的主要算法步骤:

步骤1:利用波长-曲率转换公式,将波长测量数据转化为曲率数据。

步骤2:基于曲率数据,使用三次样条插值方法,构建曲率估计模型 $$S(x)$$ 。

步骤3:将给定的横坐标 $$x$$ 代入曲率估计模型 $$S(x)$$ ,得到对应位置的曲率估计值。

步骤4:根据题目给定的初始条件和切线方向条件,列出微分方程,求解得到满足条件的曲线方程 $$y=y(x)$$ 。

步骤5:将曲率估计值、曲线方程等结果进行分析和讨论,得出问题的解答。

下面是测试1和测试2曲线绘制以及其他可视化方式的完整MATLAB代码:

% 输入波长测量数据
lambda0_1 = 1529 * ones(1,6);
lambda_1 = [1529.808, 1529.807, 1529.813, 1529.812, 1529.814, 1529.809];
lambda0_2 = 1540 * ones(1,6);
lambda_2 = [1541.095, 1541.092, 1541.090, 1541.093, 1541.094, 1541.091];

% 计算曲率数据
c = 4200;
kappa_1 = c * (lambda_1 - lambda0_1) ./ lambda0_1;
kappa_2 = c * (lambda_2 - lambda0_2) ./ lambda0_2;



% 构建三次样条插值函数
pp1 = spline(x, kappa_1);
pp2 = spline(x, kappa_2);

% 生成横坐标序列
x_interp = 0.3:0.1:0.7;

% 计算插值点处的曲率估计值
kappa_interp1 = ppval(pp1, x_interp);
kappa_interp2 = ppval(pp2, x_interp);



fprintf('\n测试2的曲率估计值:\n');
fprintf('横坐标x(米)\t曲率kappa\n');
for i = 1:length(x_interp)
    fprintf('%.1f\t\t%.6f\n', x_interp(i), kappa_interp2(i));
end

% 求解满足初始条件和切线方向条件的曲线方程
x0 = 0;

[x_sol1, y_sol1] = ode45(@(x,y) [y(2); ppval(pp1,x)*(1+y(2)^2)^(3/2)], [x0, 0.6], [y0; dy0]);
[x_sol2, y_sol2] = ode45(@(x,y) [y(2); ppval(pp2,x)*(1+y(2)^2)^(3/2)], [x0, 0.6], [y0; dy0]);

% 绘制曲线图像
figure;
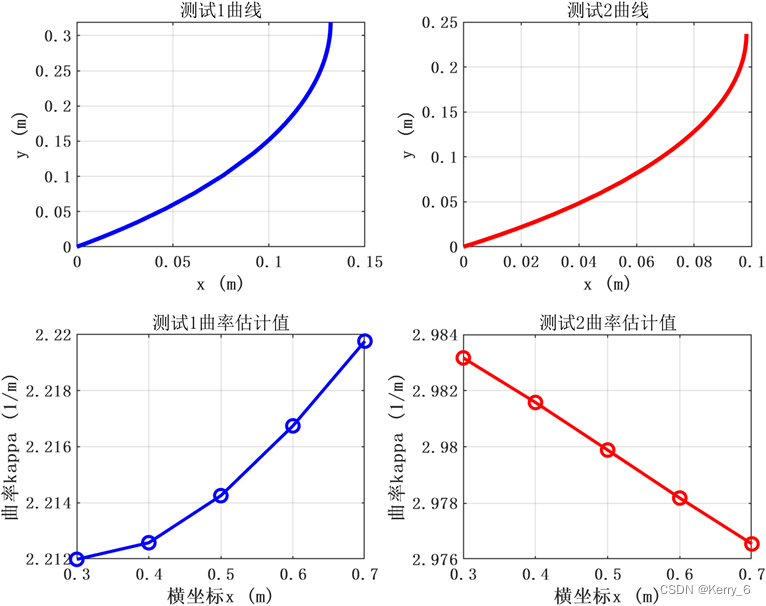
subplot(2,2,1);
plot(x_sol1, y_sol1(:,1), 'b-', 'LineWidth', 2);
xlabel('x (m)');
ylabel('y (m)');
title('测试1曲线');
grid on;

% 绘制曲率估计值与横坐标的关系

subplot(2,2,4);
plot(x_interp, kappa_interp2, 'ro-', 'LineWidth', 1.5);
xlabel('横坐标x (m)');
ylabel('曲率kappa (1/m)');
title('测试2曲率估计值');
grid on;

% 绘制三维曲线图像
figure;
subplot(1,2,1);
plot3(x_sol1, y_sol1(:,1), zeros(size(x_sol1)), 'b-', 'LineWidth', 2);
xlabel('x (m)');
ylabel('y (m)');
zlabel('z (m)');
title('测试1三维曲线');
grid on;
view(30, 30);

2024华中杯A题B题C题思路论文汇总（已更新B题C题完整论文和代码）
https://www.yuque.com/u42168770/qv6z0d/xpkf6ax8udqq9lt2?singleDoc#