2024电工杯数学建模思路 - 案例：ARIMA模型-EW帮帮网

文章目录

0 前言
1 基本概念
2 自回归（AR）部分
3 差分（I）部分
4 移动平均（MA）部分
5 ARIMA模型的组合
6 参数选择
7 模型拟合与预测
8 示例代码
9 模型优缺点
10 建模资料

0 前言

2024中国电机工程学会杯数学建模赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog

1 基本概念

ARIMA模型是一种广泛应用于时间序列数据预测的统计模型，全称为自回归差分移动平均模型（AutoRegressive Integrated Moving Average Model）。它结合了自回归（AR）模型、差分（I）操作和移动平均（MA）模型的特点，能够有效处理和预测具有特定统计特性的时间序列数据。下面将详细介绍ARIMA模型的基本组成和原理。

2 自回归（AR）部分

自回归（AR）部分是ARIMA模型中的关键组成部分之一，它描述了时间序列当前值与其过去值之间的关系。自回归模型的基本思想是，时间序列中的每一个值都是其前几个时间点值的线性组合加上一个随机扰动项。这种模型可以捕捉时间序列的动态特征和依赖结构。

AR模型的数学表达

一个AR模型可以表示为：

$X_t$ = c + $\phi_1$ $X_{t-1}$ + $\phi_2 X_{t-2}$ + … + $\phi_p X_{t-p}$ + $\epsilon_t$

其中：

$X_t$ 是时间序列在时间点t的观测值。
$c$ 是常数项（也称为截距）。
$\phi_1$ , $\phi_2$ , …, $\phi_p$ 是自回归系数，表示时间序列当前值与其前p个时间点值的线性关系。
$\epsilon_t$ 是随机扰动项，通常假设为白噪声过程，即均值为0且具有恒定方差的随机变量序列，且之间相互独立。
$p$ 是模型的阶数，即考虑多少个过去的观测值来预测当前的值。

AR模型的特点

线性关系：AR模型假设时间序列的当前值与其过去的值之间存在线性关系。这意味着模型可以通过调整系数来近似时间序列的真实路径。
阶数（p）：AR模型的阶数决定了模型复杂度和需要考虑的历史信息量。阶数的选择通常基于统计检验和信息准则，如AIC（赤池信息准则）或BIC（贝叶斯信息准则）。
平稳性：AR模型通常适用于平稳时间序列。如果时间序列是非平稳的，可能需要通过差分等方法将其转换为平稳序列，然后再应用AR模型。
预测能力：AR模型可以用于预测时间序列的未来值。一旦模型参数被估计出来，就可以通过已知的历史数据来预测未来的值。

AR模型的参数估计

在实际应用中，估计AR模型的参数通常涉及以下步骤：

模型识别：通过观察时间序列的自相关函数（ACF）和偏自相关函数（PACF）图来确定合适的阶数p。
参数估计：使用最大似然估计（MLE）或其他方法来估计模型参数 $\phi_1$ , $\phi_2$ , …, $\phi_p$ 和常数项 $c$ 。
模型检验：对估计的模型进行检验，以确保模型能够充分捕捉时间序列的特征。这可能包括残差分析、模型拟合优度检验等。
预测：利用拟合好的AR模型进行预测，并评估预测的准确性。

AR模型是时间序列分析中的一个强大工具，可以用于多种领域的数据分析和预测任务。然而，选择合适的模型阶数和参数对于建立有效的AR模型至关重要。在实际应用中，可能需要结合领域知识和多种模型选择准则来确定最佳的AR模型。

3 差分（I）部分

ARIMA模型中的差分（I）部分是处理非平稳时间序列的关键步骤。非平稳时间序列是指其统计特性（如均值、方差等）随时间变化的数据序列。为了使时间序列平稳，从而能够应用ARIMA模型中的自回归（AR）和移动平均（MA）部分，我们需要对原始时间序列进行差分处理。

差分是一种将时间序列转换为平稳序列的数学操作。对于一个时间序列 $X_t$ ，其一阶差分定义为：

$\Delta X_t$ = $X_t$ - $X_{t-1}$

这里的 $\Delta X_t$ 表示时间序列在时间点t的变化量，即当前值与前一个时间点值的差。如果一阶差分后的序列仍然非平稳，可能需要进行更高阶的差分。例如，二阶差分定义为：

$\Delta^2 X_t$ = $\Delta X_t$ - $\Delta X_{t-1}$

差分的主要目的是消除时间序列中的长期趋势和季节性变化，使得序列的均值和方差随时间保持不变，即达到平稳状态。平稳时间序列是ARIMA模型建立和预测的基础。

差分的步骤

确定差分次数：首先，需要通过图形分析（如趋势图和自相关图）或统计检验（如ADF检验）来确定时间序列是否平稳，以及需要进行几次差分才能达到平稳。
执行差分操作：根据确定的差分次数，对原始时间序列进行相应次数的差分操作。
检验平稳性：对差分后的时间序列再次进行平稳性检验，确保序列已经平稳。
建立ARIMA模型：在差分后平稳的时间序列上，建立ARIMA模型的AR和MA部分。

在ARIMA模型中，差分部分通常用字母“I”表示，后面的数字d表示差分的次数。例如，ARIMA(1, d, 1)模型表示该模型包含一阶自回归（AR）部分，d次差分，以及一阶移动平均（MA）部分。

示例

假设我们有一个时间序列数据集，通过ADF检验发现它是非平稳的。我们可以首先对其进行一阶差分，然后再次进行ADF检验。如果差分后的时间序列平稳，我们就可以在差分后的数据上建立AR和MA模型。最后，我们可以使用建立的ARIMA模型进行预测，并根据需要将预测结果通过反向差分恢复到原始时间序列的尺度。

总之，差分是ARIMA模型中处理非平稳时间序列的重要步骤，它使得模型能够捕捉时间序列的内在特性，并进行有效的预测。

4 移动平均（MA）部分

移动平均（MA）部分是ARIMA模型中的另一个关键组成部分，它描述了时间序列当前值与其过去误差项之间的关系。移动平均模型的基本思想是，时间序列中的每一个值可以通过前几个时间点的误差项的线性组合来表示。

MA模型的数学表达

一个MA模型可以表示为：

$X_t$ = $\mu$ + $\epsilon_t$ + $\theta_1$ $\epsilon_{t-1}$ + $\theta_2$ $\epsilon_{t-2}$ + … + $\theta_q$ $\epsilon_{t-q}$

其中：

$X_t$ 是时间序列在时间点t的观测值。
$\mu$ 是常数项（也称为均值）。
$\epsilon_t$ 是时间序列在时间点t的随机误差项，通常假设为白噪声过程，即均值为0且具有恒定方差的随机变量序列。
$\theta_1$ , $\theta_2$ , …, $\theta_q$ 是移动平均系数，表示时间序列当前值与其前q个时间点误差项的线性关系。
$q$ 是模型的阶数，即考虑多少个过去的误差项来预测当前的值。

MA模型的特点

线性关系：MA模型假设时间序列的当前值与其过去的误差项之间存在线性关系。这意味着模型可以通过调整系数来近似时间序列的真实路径。
阶数（q）：MA模型的阶数决定了模型复杂度和需要考虑的历史误差项的数量。阶数的选择通常基于统计检验和信息准则。
平稳性：MA模型通常适用于平稳时间序列。如果时间序列是非平稳的，可能需要通过差分等方法将其转换为平稳序列，然后再应用MA模型。
预测能力：MA模型可以用于预测时间序列的未来值。一旦模型参数被估计出来，就可以通过已知的历史数据来预测未来的值。

MA模型的参数估计

在实际应用中，估计MA模型的参数通常涉及以下步骤：

模型识别：通过观察时间序列的偏自相关函数（PACF）图来确定合适的阶数q。
参数估计：使用最大似然估计（MLE）或其他方法来估计模型参数 $\theta_1$ , $\theta_2$ , …, $\theta_q$ 和常数项 $\mu$ 。
模型检验：对估计的模型进行检验，以确保模型能够充分捕捉时间序列的特征。这可能包括残差分析、模型拟合优度检验等。
预测：利用拟合好的MA模型进行预测，并评估预测的准确性。

MA模型是时间序列分析中的一个重要工具，可以用于多种领域的数据分析和预测任务。然而，选择合适的模型阶数和参数对于建立有效的MA模型至关重要。在实际应用中，可能需要结合领域知识和多种模型选择准则来确定最佳的MA模型。在ARIMA模型中，MA部分与AR部分共同作用，提供了一种强大的方法来捕捉时间序列的动态特性和预测未来值。

5 ARIMA模型的组合

ARIMA模型通过组合AR、I、MA三部分来处理时间序列数据。一个ARIMA(p, d, q)模型可以表示为：

$(1$ - $\phi_1 z$ - $\phi_2 z^2 - ... - \phi_p z^p)$ $1 - z)^d X_t$ = $\mu$ + $\theta_1$ $\epsilon_{t-1}$ + $\theta_2$ $\epsilon_{t-2}$ + … + $\theta_q$ $\epsilon_{t-q}$ + $\epsilon_t$

在这个方程中：

$z$ 是后移算子， $z^k X_t$ 表示时间序列在k个时间点之前的值。
$\phi_1$ , $\phi_2$ , …, $\phi_p$ 是自回归部分的系数。
$\epsilon_t$ 是白噪声误差项。
$\mu$ 是常数项（或均值）。
$\theta_1$ , $\theta_2$ , …, $\theta_q$ 是移动平均部分的系数。
$d$ 是使时间序列达到平稳状态所需的差分次数。

ARIMA模型的组合步骤

模型识别：首先，需要识别时间序列的性质，包括是否平稳、是否存在明显的趋势或季节性等。这通常通过图形分析（如时间序列图、自相关图和偏自相关图）和统计检验（如ADF检验）来完成。
差分处理：如果时间序列非平稳，需要进行差分处理，使序列平稳。差分的次数d根据时间序列的特性确定。
参数选择：确定AR部分的阶数p和MA部分的阶数q。这通常通过分析时间序列的自相关图（ACF）和偏自相关图（PACF）来完成。
模型拟合：使用选定的参数（p, d, q）来拟合ARIMA模型。这可以通过最大似然估计或其他优化方法来完成。
模型检验：对拟合的模型进行检验，包括残差分析、模型拟合优度检验等，以确保模型的有效性和准确性。
预测：利用拟合好的ARIMA模型进行预测。模型的预测能力可以通过交叉验证或对未来数据的预测来评估。

应用示例

假设我们有一个时间序列数据集，我们首先通过图形分析和ADF检验确定它是非平稳的。接下来，我们对数据进行一阶差分，并再次检验平稳性。然后，我们通过ACF和PACF图确定AR部分和MA部分的阶数。假设我们选择了ARIMA(1, 1, 2)模型，我们可以使用相应的统计软件（如R、Python的statsmodels库等）来拟合模型，并进行预测。

ARIMA模型的组合提供了一种灵活且强大的方法来处理和预测各种类型的时间序列数据，无论是平稳的还是非平稳的，都可以找到合适的ARIMA模型来进行分析和预测。

6 参数选择

ARIMA模型的关键步骤之一是选择合适的p、d、q参数。这通常通过观察时间序列的自相关函数（ACF）和偏自相关函数（PACF）图来实现。ACF图反映了时间序列在不同时间滞后下的相关性，而PACF图则显示了时间序列与其过去值之间的直接关系。

7 模型拟合与预测

确定参数后，可以使用极大似然估计或其他估计方法来估计模型参数，并拟合ARIMA模型。拟合好的模型可以用来进行历史数据的诊断检验，以及未来值的预测。

ARIMA模型因其强大的理论基础和良好的预测性能，在时间序列分析领域得到了广泛的应用。然而，需要注意的是，ARIMA模型假设时间序列的未来值只依赖于其过去的值，因此对于某些受外部因素影响较大的时间序列，可能需要考虑更复杂的模型或引入其他变量。

8 示例代码

为了提供一个可运行的ARIMA模型示例代码，我们将使用Python的statsmodels库。以下是一个简单的示例，展示如何使用ARIMA模型对合成的时间序列数据进行拟合和预测。注意，这个示例是在一个假设的数据集上进行的，实际应用中需要使用自己的数据集。

确保已经安装了statsmodels和pandas库。如果没有安装，可以使用以下命令安装：

pip install statsmodels pandas

ARIMA模型的示例代码：

import pandas as pd
import numpy as np
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.stattools import adfuller
import matplotlib.pyplot as plt

# 创建合成的时间序列数据
np.random.seed(100)  # 为了结果的可重复性，设置随机种子
n = 100  # 数据点的数量
t = np.arange(n)  # 创建时间序列的时间索引
data = np.random.randn(n).cumsum()  # 创建一个随机游走时间序列
df = pd.DataFrame(data, index=pd.date_range(start='1/1/2020', periods=n))  # 将数据转换为DataFrame

# 检查时间序列的平稳性
result = adfuller(df)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])

# 根据ADF检验的结果，判断是否需要进行差分
# 这里我们的数据已经是随机游走，可以认为是平稳的，但为了演示，我们进行一阶差分
df_diff = df.diff().dropna()

# 确定ARIMA模型的参数(p, d, q)
# 这通常通过观察ACF和PACF图来完成，但在这里我们将直接指定参数
# 假设我们选择了ARIMA(2, 1, 2)模型
model = ARIMA(df_diff, order=(2, 1, 2))

# 拟合ARIMA模型
results = model.fit()

# 打印模型的摘要信息
print(results.summary())

# 使用拟合的模型进行预测
# 预测未来12个时间点的值
forecast = results.get_forecast(steps=12)
forecast_mean = forecast.predicted_mean
forecast_ci = forecast.conf_int()

# 绘制原始数据和预测结果
plt.figure(figsize=(12, 6))
plt.plot(df.index, df, label='Observed', color='blue', alpha=0.5)
plt.plot(forecast_mean.index, forecast_mean, label='Forecast', color='red', alpha=0.8)
plt.fill_between(forecast_mean.index, forecast_ci.iloc[:, 0], forecast_ci.iloc[:, 1], color='pink', alpha=0.3)
plt.title('ARIMA Model Forecast')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()

首先创建了一个合成的时间序列数据集，然后进行了ADF检验以判断其是否平稳。对数据进行了一阶差分，并选择了一个ARIMA(2, 1, 2)模型进行拟合。最后使用拟合的模型进行了未来12个时间点的预测，并将结果绘制出来。
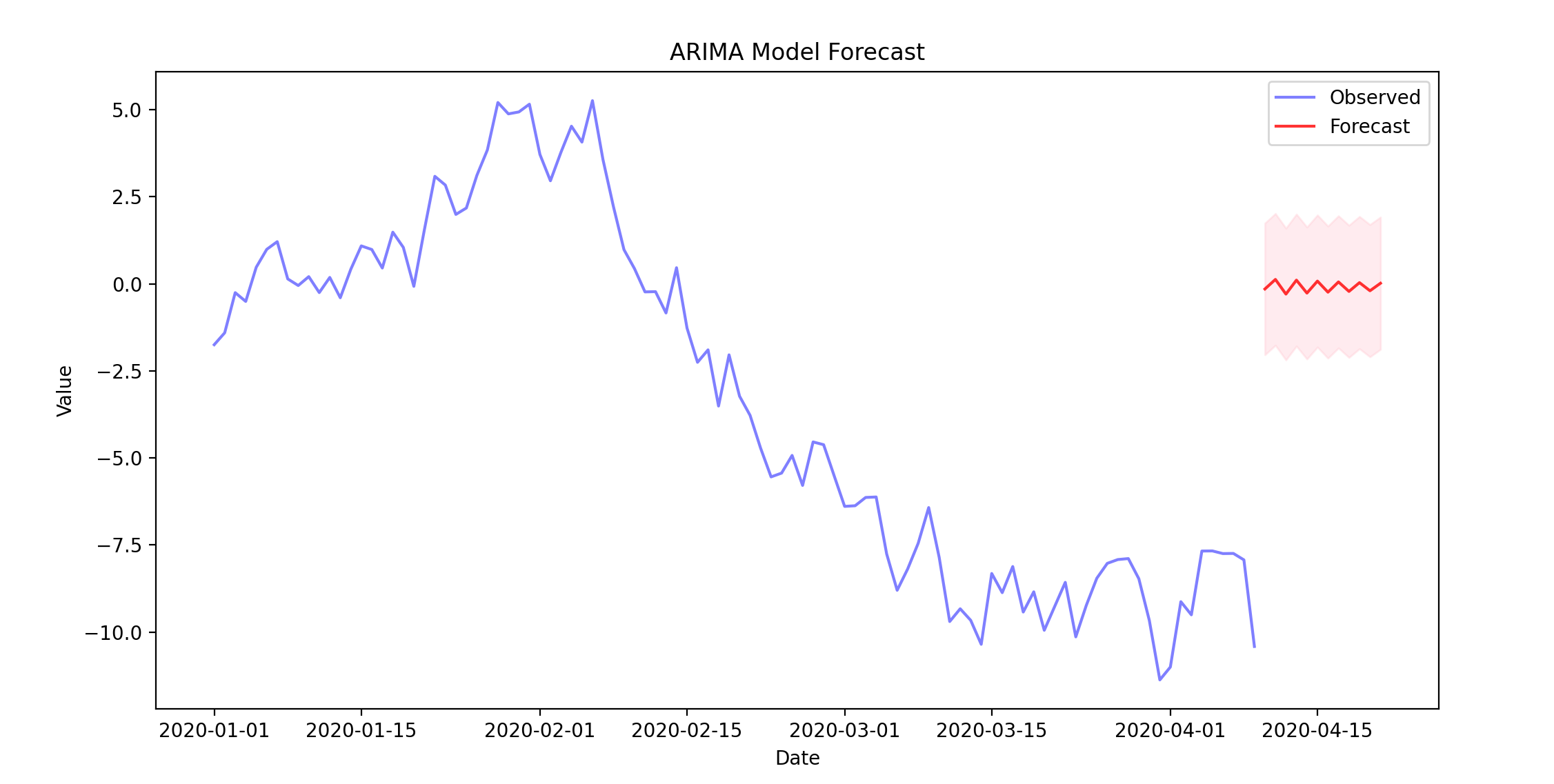
在这里插入图片描述
这个示例是在一个合成的数据集上进行的。在实际应用中，需要根据自己的数据集来确定ARIMA模型的参数，并进行模型的拟合和预测。

9 模型优缺点

ARIMA模型是一种广泛应用于时间序列分析和预测的统计模型，它具有一些明显的优点，同时也存在一些局限性。

优点

简单易懂：ARIMA模型结构清晰，易于理解和解释，只需内生变量而不需要外生变量。
处理非平稳性：通过差分操作，ARIMA能够有效处理非平稳时间序列数据，使其平稳后进行分析。
考虑历史数据：模型能够利用历史数据来预测未来趋势，捕捉时间序列的数据特征。
灵活性：ARIMA模型可以适应多种时间序列的特性，通过调整p（自回归项）、d（差分阶数）和q（移动平均项）参数来适应不同的数据需求。
可解释性：模型参数具有明确的统计学含义，可以帮助理解时间序列的动态特性。

缺点

平稳性要求：ARIMA模型要求时间序列数据是平稳的，对于非平稳数据需要进行预处理，如差分等，这可能增加模型构建的复杂性。
线性模型限制：ARIMA本质上是一个线性模型，无法捕捉数据中的非线性关系，对于具有复杂非线性特征的时间序列预测效果可能不佳。
过拟合风险：如果模型参数选择不当，可能存在过拟合的问题，需要通过模型选择和参数调整来避免。
单变量限制：ARIMA模型通常用于单变量时间序列，无法同时考虑多个相关因素的影响。
长期预测局限：对于长期预测，ARIMA模型可能效果不理想，因为它主要依赖历史数据，没有考虑未来可能发生的外部影响。

10 建模资料

在这里插入图片描述

2024电工杯数学建模思路 - 案例：ARIMA模型