文章目录
存储结构
队列是只允许在一端进行插入,在另一端进行删除操作的线性表。
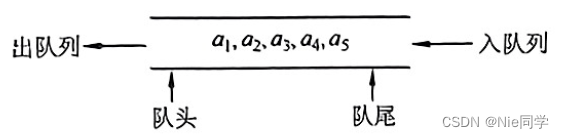
物理结构
顺序队列
利用静态数组实现,并需要记录队头和队尾指针,且队列的大小不可改变。
typedef struct {
int data; // 数据域
int front, rear; // 队头队尾指针域
} SqQueue;
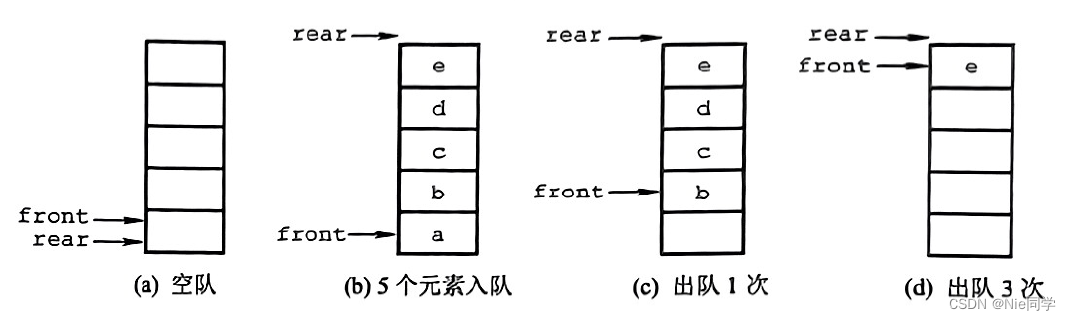
在图d队列中,仅有一个元素。这时入队出现“上溢出”,但这种溢出并不是真正的溢出,在data 数组中依然存在可以存放元素的空位置,所以是一种 “假溢出”,极大的浪费了存储空间以及大小不可扩充的问题 。
循环队列
为了解决 “假溢出” 的问题,我们引入循环队列。将顺序队列想象成一个环状的空间,将存储队列从逻辑上视为一个环,称之为循环队列。
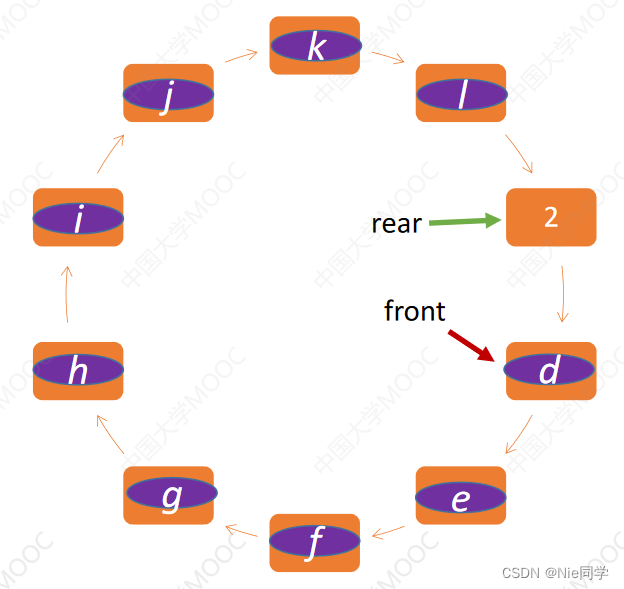
定义与顺序队列一样,区别在于判满和判空的逻辑不同。解决了“假溢出”的问题,但是没有解决队列不可扩充的问题。
链式队列
利用单链表实现,需要头指针和队尾指针,解决了顺序队列中队列的大小不可扩充的问题。

定义结点
typedef struct LinkNode {
int data; // 数据域
struct LinkNode *next; // 指针域
} LinkNode;
定义队列
typedef struct {
LinkNode *front, *rear; // 定义队头队尾指针
} LinkQueue;
双端队列
双端队列是指允许两端都可以进行插入和删除操作的线性表,双端队列两端的地位是平等的,为了方便理解,将左端也视为前端,右端也视为后端。
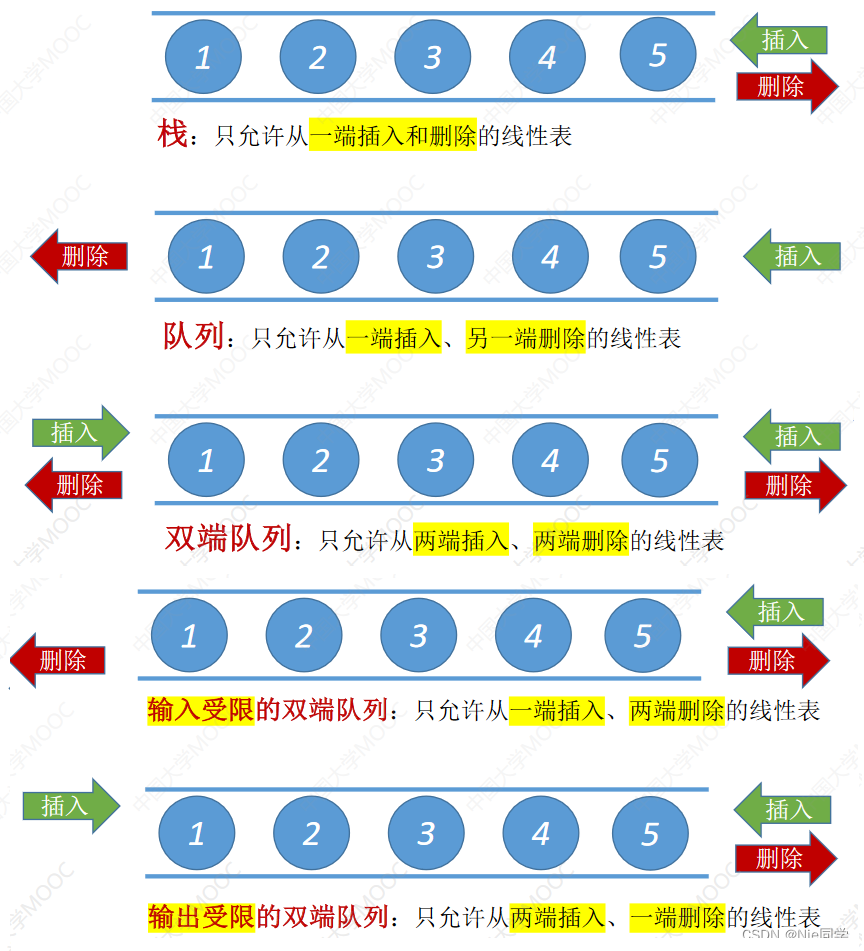
链式存储
typedef struct DequeNode { // 定义双端队列结点
int data; // 数据域
struct DequeNode *pre, *next; // 前后指针域
} DequeNode;
typedef struct { // 定义双端队列
DequeNode *front, *rear; // 头尾指针域
} Deque;
数据的操作
顺序队列的基本操作
初始化
void InitQueue(SqQueue &q)
{
q.front = q.rear = 0;
}
判断队列为空
bool isEmpty(SqQueue q)
{
if (q.front == q.rear) return true;
return false;
}
判断队列为满
bool isFull(SqQueue q)
{
if (q.rear == Maxsize) return true;
return false;
}
入队列
bool EnQueue(SqQueue &q, int &x)
{
if (!isFull(q))
{
q.data[q.rear ++ ] = x;
return true;
}
return false;
}
出队列
bool DeQueue(SqQueue &q, int &x)
{
if (!isEmpty(q))
{
x = q.data[q.front ++ ];
return true;
}
return false;
}
循环队列的基本操作
初始化
void InitQueue(SqQueue &q)
{
q.rear = q.front = 0;
}
判空/判满/入队/出队(三种处理方式)
若用循环队列的话,判断队空的条件是Q.front==Q.rear,判断队满的条件也是Q.front==Q.rear。这就会区分不出来到底是队空还是队满。
为了区分是队空还是队满的情况,有三种处理方式:
- 牺牲一个单元来区分队空和队满,入队时少用一个队列单元,约定以“队头指针在队尾指针的下一位置作为队满的标志”。
bool isEmpty(SqQueue q)
{
if (q.rear == q.front) return true;
return false;
}
bool isFull(SqQueue q)
{
if ((q.rear + 1) % Maxsize == q.front) return true;
return false;
}
bool EnQueue(SqQueue &q, int x)
{
if (!isFull(q))
{
q.data[q.rear] = x;
q.rear = (q.rear + 1) % Maxsize;
return true;
}
return false;
}
bool DeQueue(SqQueue &q, int &x)
{
if (!isEmpty(q))
{
x = q.data[q.front];
q.front = (q.front + 1) % Maxsize;
return true;
}
return false;
}
- 类型中增设
size数据成员,表示元素个数。
typedef struct {
int data[Maxsize]; // 数据域
int front, rear; // 队头队尾指针域
int size; // 队中元素个数
} SqQueue;
void InitQueue(SqQueue &q)
{
q.front = q.rear = 0;
q.size = 0;
}
bool isEmpty(SqQueue q)
{
if (q.size == Maxsize) return true;
return false;
}
bool isFull(SqQueue q)
{
if (q.size == 0) return true;
return false;
}
bool EnQueue(SqQueue &q, int x)
{
if (!isFull(q))
{
q.data[q.rear] = x;
q.rear = (q.rear + 1) % Maxsize;
q.size ++ ;
return true;
}
return false;
}
bool DeQueue(SqQueue &q, int &x)
{
if (!isFull(q))
{
x = q.data[q.front];
q.front = (q.front + 1) % Maxsize;
q.size -- ;
return true;
}
return false;
}
- 类型中增设
tag数据成员,以区分是队满还是队空。删除成功置tag=0,插入成功置tag=1。只有删除操作才能使得队空,只有插入操作才能使得队满。
typedef struct {
int data[Maxsize]; // 数据域
int front, rear; // 队头队尾指针
int tag; // 标志域
} SqQueue;
void InitQueue(SqQueue &q)
{
q.front = q.rear = 0;
q.tag = 0;
}
bool isEmpty(SqQueue q)
{
if (q.rear == q.front && tag == 0) return true;
return false;
}
bool isFull(SqQueue q)
{
if (q.rear == q.front && tag == 1) return true;
return false;
}
bool EnQueue(SqQueue &q, int x)
{
if (!isFull(q, x))
{
q.data[q.rear] = x;
q.rear = (q.rear + 1) % Maxsize;
q.tag = 1;
return true;
}
return false;
}
bool DeQueue(SqQueue &q, int &x)
{
if (!isEmpty(q))
{
x = q.data[q.front];
q.front = (q.front + 1) % Maxsize;
q.tag = 0;
return true;
}
return false;
}
链式队列的基本操作
初始化
void InitQueue(LinkQueue &q)
{
q.rear = q.front = (LinkNode *) malloc (sizeof(LinkNode));
q.front->next = NULL;
}
判空
bool isEmpty(LinkQueue q)
{
if (q.front == q.rear) return true;
return false;
}
入队
bool EnQueue(LinkQueue &q, int x)
{
LinkNode *t = (LinkNode *) malloc (sizeof(LinkNode));
t->data = x;
t->next = NULL;
q.rear->next = t;
q.rear = t;
return true;
}
出队
bool DeQueue(LinkQueue &q, int &x)
{
if (!isEmpty(q))
{
LinkNode *t = q.front->next;
x = t->data;
q.front->next = t->next;
if (q.rear == t) // 若只有一个结点,删除后使其变为空队列
q.rear = q.front;
free(t);
return true;
}
return false;
}
双端队列的基本操作
初始化
void InitQueue(Deque &q)
{
q.front = q.rear = NULL;
}
判空
bool isEmpty(Deque q)
{
if (q.front == NULL && q.rear == NULL) return true;
return false;
}
队头插入
bool InsertFront(Deque &q, int x)
{
DequeNode *newNode = (DequeNode *) malloc(sizeof(DequeNode));
newNode->data = x;
newNode->pre = NULL;
newNode->next = q->front;
if (isEmpty(q))
q->rear = newNode;
else
q->front->pre = newNode;
q->front = newNode;
return true;
}
队尾插入
bool InsertRear(Deque &q, int x)
{
DequeNode *newNode = (DequeNode *) malloc(sizeof(DequeNode));
newNode->data = x;
newNode->next = NULL;
newNode->pre = q->rear;
if (isEmpty(q))
q->front = newNode;
else
q->rear->next = newNode;
q->rear = newNode;
return true;
}
队头删除
bool DeleteFront(Deque &q, int &x)
{
if (isEmpty(q)) return false;
DequeNode *temp = q->front;
x = temp->data;
q->front = q->front->next;
if (q->front) // 如果队列不为空,更新新的队首节点的 prev 指针
q->front->prev = NULL;
else // 如果删除后队列为空,更新队尾指针
q->rear = NULL;
free(temp);
return true;
}
队尾删除
bool DeleteRear(Deque &q, int &x)
{
if (isEmpty(q)) return false;
DequeNode *temp = q->rear;
x = temp->data;
q->rear = q->rear->prev;
if (q->rear) // 如果队列不为空,更新新的队尾节点的 next 指针
q->rear->next = NULL;
else // 如果删除后队列为空,更新队首指针
q->front = NULL;
free(temp);
return true;
}
数据结构的应用
队列在层次遍历中的应用
队列适用于逐层或逐行处理,使用队列是为了保存下一步的处理顺序。下面用二叉树(见图 3.17)层次遍历的例子,说明队列的应用。
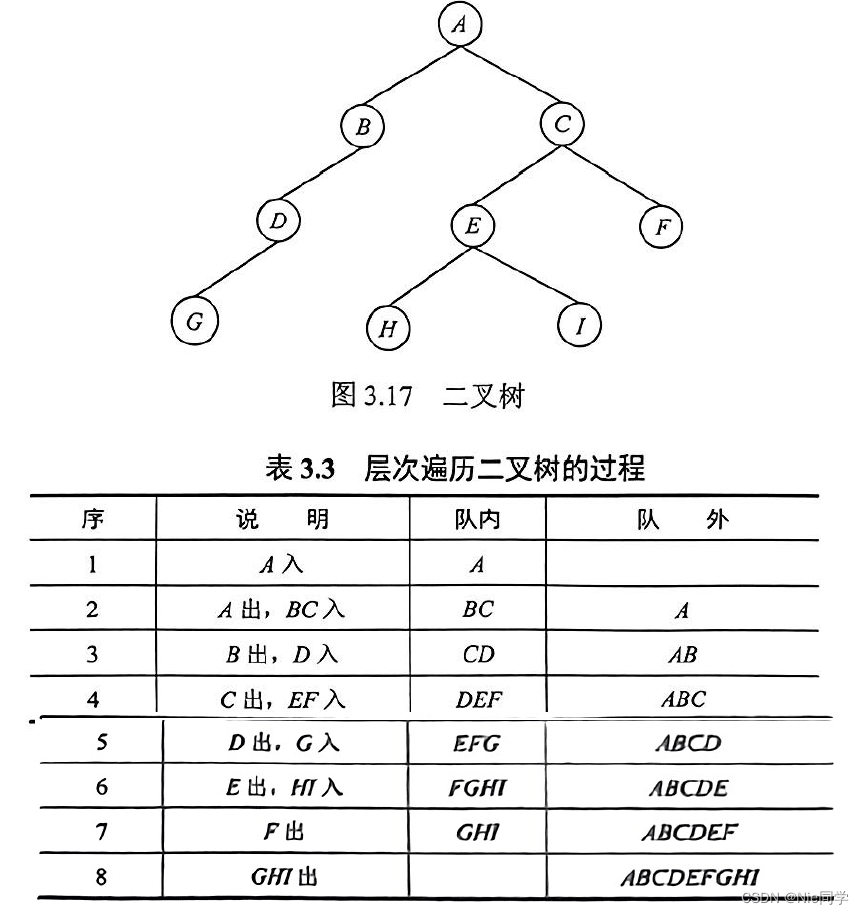
该过程的简单描述如下:
① 根结点入队,
② 若队空(所有结点都已处理完毕),则结束遍历;否则重复③操作。
③队列中第一个结点出队,并访问之。若其有左孩子,则将左孩子入队;若其有右孩子,则将右孩子入队,返回②。
void InverLevel(BiTree T)
{
SqQueue q, InitQueue(q);
BiTNode *p = T; // 遍历指针
EnQueue(q, p);
while (!isEmpty(q))
{
DeQueue(q, p);
visit(p);
if (p->lchild) Enqueue(q, p->lchild);
if (p->rchild) Enqueue(q, p->rchild);
}
}
队列在计算机系统中的应用(OS)
缓冲区的逻辑结构:
主机输出数据给打印机打印,输出数据的速度比打印数据的速度要快得多,因为速度不匹配,若直接把输出的数据送给打印机打印,则显然是不行的。解决的方法是设置一个打印数据缓冲区,主机把要打印输出的数据依次写入这个缓冲区,写满后就暂停输出,转去做其他的事情。打印机就从缓冲区中按照先进先出的原则依次取出数据并打印,打印完后再向主机发出请求。主机接到请求后再向缓冲区写入打印数据。这样做既保证了打印数据的正确,又使主机提高了效率。由此可见,打印数据缓冲区中所存储的数据就是一个队列。
队列出队入队操作的应用:
CPU资源的竞争就是一个典型的例子。在一个带有多终端的计算机系统上,有多个用户需要CPU各自运行自己的程序,它们分别通过各自的终端向操作系统提出占用CPU 的请求。操作系统通常按照每个请求在时间上的先后顺序,把它们排成一个队列,每次把CPU分配给队首请求的用户使用。当相应的程序运行结束或用完规定的时间间隔后,令其出队,再把CPU 分配给新的队首请求的用户使用。这样既能满足每个用户的请求,又使CPU能够正常运行。