Python 全栈体系【四阶】（四十八）

第五章 深度学习

十一、扩散模型

1. 概述

扩散模型（Diffusion Model）是最近几年流行起来的一种新的图像生成模式，扩散模型的原理类似给图片去噪，通过学习给一张图片去噪的过程来理解有意义的图像是如何生成，因此扩散模型生成的图片相比 GAN 模型精度更高，更符合人类视觉和审美逻辑，同时随着样本数量和深度学习时长的累积，扩散模型展现出对艺术表达风格较好的模仿能力。

扩散模型( Diffusion Models )的灵感来自非平衡热力学。定义了扩散步骤的马尔可夫链，以缓慢地将随机噪声添加到数据中，然后学习逆向扩散过程以从噪声中构造所需的数据样本。下图对几种主要图像生成技术原理进行了对比：

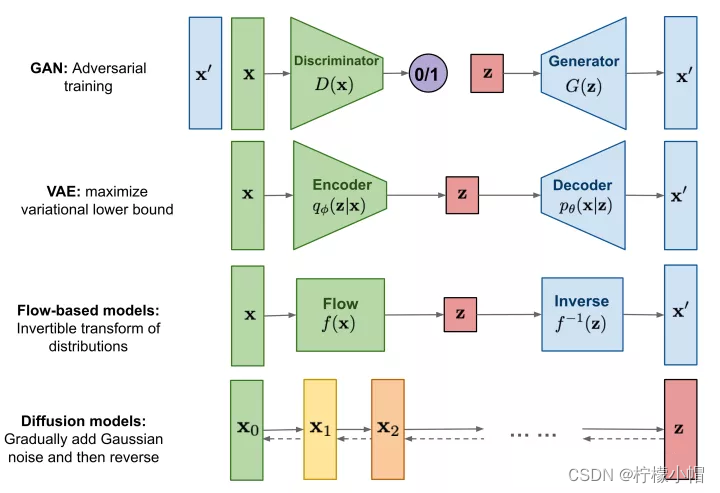
GAN模型（上图第一行）通过使得生成器（Generator）生成的图片$x^{\prime }$尽可能逼近真实图片$x$，从而达到以假乱真的目的，本质上还是去生成和真实图片接近的新图片，因此GAN生成的图片可能没有太多亮点。而DDPM是拟合整个从真实图片$x_0$到随机高斯噪声$Z$的过程，再通过反向过程生成新的图片。

2. DDPM（2020）

DDPM全称是Denoising Diffusion Probabilistic Models（去噪扩散概率模型），2020年由加州大学伯克利分校的研究人员提出。

2.1 基本原理

DDPM包括两个过程：前向过程（forward process）和反向过程（reverse process），其中前向过程又称为扩散过程（diffusion process），其作用是不断向图像中添加高斯噪声，直到图像逐渐被噪声掩盖，变成完全（或近似完全）的高斯噪声图像；反向在前向过程生成的噪声图像上，通过预测噪声，将噪声逐步分离，直到还原为原图的过程。

2.1.1 前向过程

前向过程就是对原始图片$x_0$中不断添加高斯噪声的过程，当经过T次添加后，生成随机噪声图像$x_T$，由$x_{t-1}$到$x_t$的过程可表示为：

$$x_t=\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}$$

其中${\alpha }_t$是一个很小的超参数，${ϵ}_{t-1}\sim N(0,1)$为高斯噪声。经过推导，最终可得到由$x_0$直接计算出$x_t$的公式：

$$x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ$$

其中${\bar{\alpha }}_t={\prod }_{i=1}^t{\alpha }_i$, ${ϵ}_t\sim N(0,1)$为高斯噪声。这样，就可以根据公式，直接由输入图像计算出随机噪声图像$x_t$，从而简化计算.

2.1.2 反向过程

反向过程是通过预测随机噪声$ϵ$，将前向过程生成的随机图像$x_t$逐步还原为原图$x_0$的过程.反向过程公式如下：

$$x_{t-1}=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))+{\sigma }_{t}z$$

其中${ϵ}_{\theta }$是噪声估计函数（一般使用神经网络模型），用于估计噪声；$\theta$是模型参数；$z\sim N(0,1)$为高斯噪声，${\sigma }_{t}z$表示预测噪声和真实噪声的误差值. DDPM模型的关键，就是训练噪声估计模型${ϵ}_{\theta }(x_t,t)$，用于估计真实噪声$ϵ$.

2.2 训练过程

DDPM的关键是训练噪声估计模型${ϵ}_{\theta }(x_t,t)$，损失函数用来表示估计噪声与真实噪声之间的误差：

$$Loss=||ϵ-{ϵ}_{\theta }(x_t,t)|{|}^2=||ϵ-{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{x}_{t-1}+\sqrt{1-{\bar{\alpha }}_t}ϵ,t)|{|}^2$$

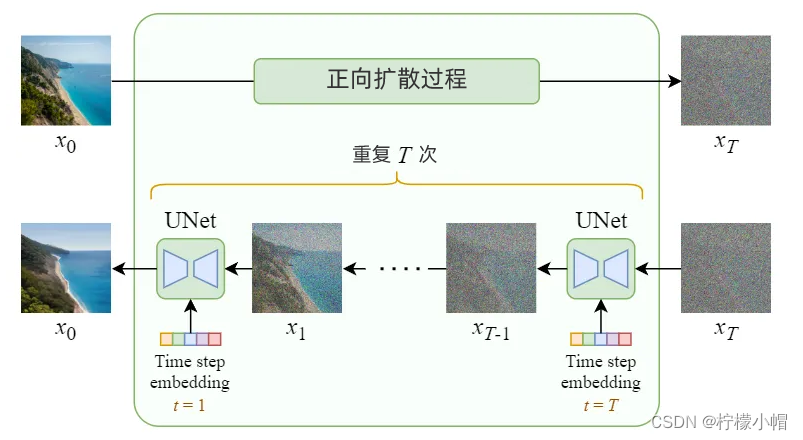
训练过程可表示为下图所示过程：

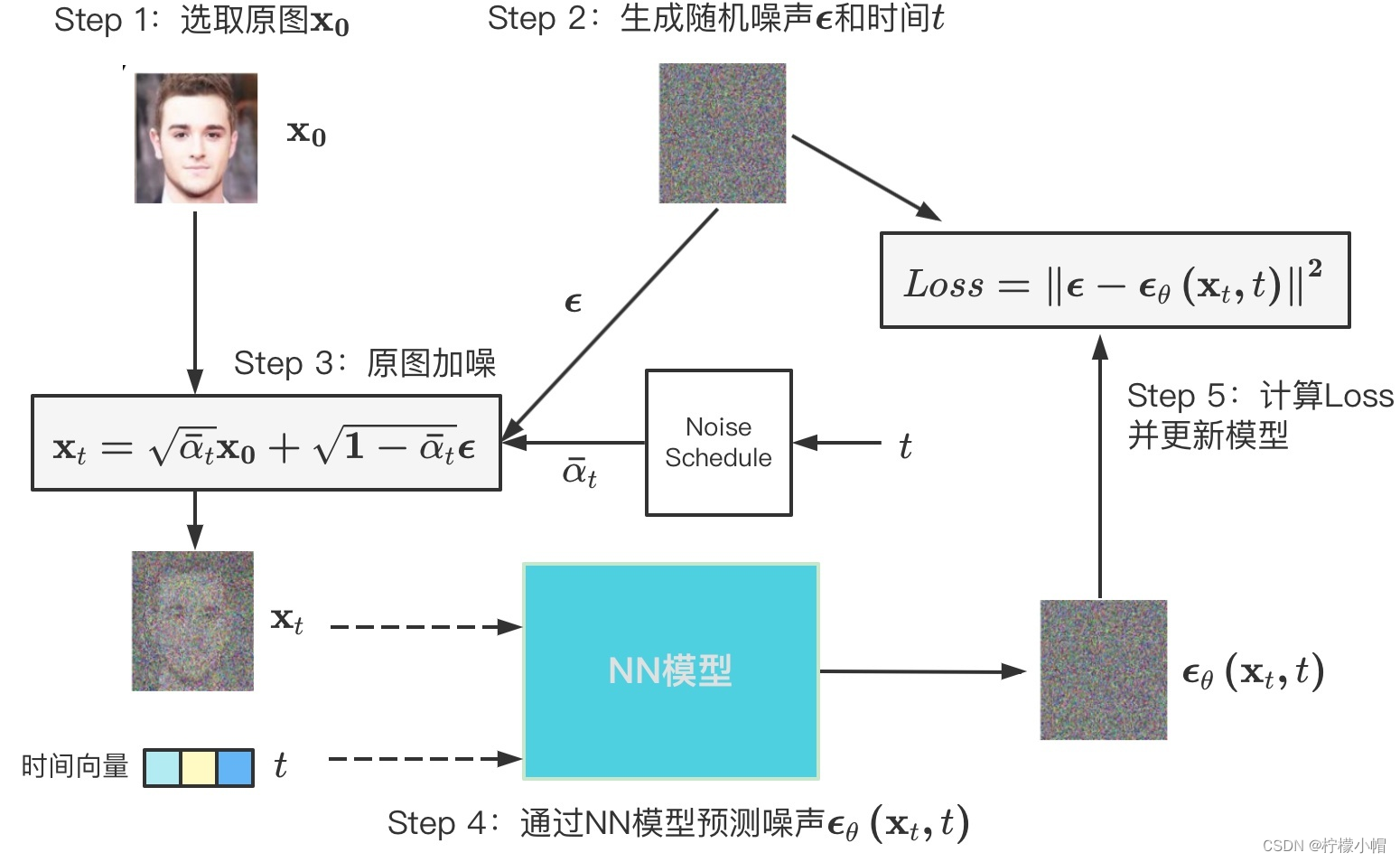
算法表示为：

• 第一步：$x_0$符合分布$q(x_0)$，也就是从训练集中采样数据
• 第二步：随机生成一个时刻$t$
• 第三步：生成标准正态分布噪声，均值为$0$，方差为$I$
• 第四步：执行梯度下降，其中${ϵ}_{\theta }$是一个神经网络

2.3 生成图像

在噪声预测模型预测出噪声后，就可以按反向过程公式（3）逐步得到最终的图片$x_0$，算法表示如下：

第一步：$x_T$从一个标准正态分布开始

第二步：从T开始到$1$，执行循环

第三步：从正态分布中采样$z$

第四步：用第三步采样的$z$乘以当前分布的标准差，再加上均值，就可以得到$x_{t-1}$，经过若干次迭代后就能得到$x_0$返回

3. Stable Diffusion（2022）

由于DDPM模型扩散过程是在图片空间里完成的，所以它的计算过程非常慢，基本无法在单个GPU上运行。

例如，一张512 x 512的彩色图像（包含3个颜色通道：红、绿、蓝），它的计算空间是786,432维。

Stable Diffusion一开始的名称是“潜在扩散模型”（Latent Diffusion Model） ，主要解决扩散模型速度问题，它的正向扩散和逆向扩散过程不是在原图像空间完成，而是将图片压缩到一个“潜空间”（latent space）中，潜空间比图片空间小了48倍，所以它可以节省大量计算，继而运行速度更快。

3.1 基本流程

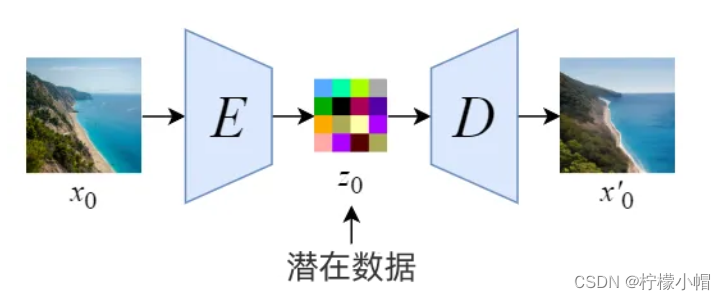
1）编码。通过使用经过训练的编码器E，将全尺寸的图像编码为低维度的潜空间中（潜空间可以理解为原图像的压缩，数据量小很多，但信息缺不产生损失，因为自然界的图像并不是完全随机的，而是有很强的规律性）；

2）解码。通过使用经过训练的解码器D，根据潜空间还原为图像。如下图所示：

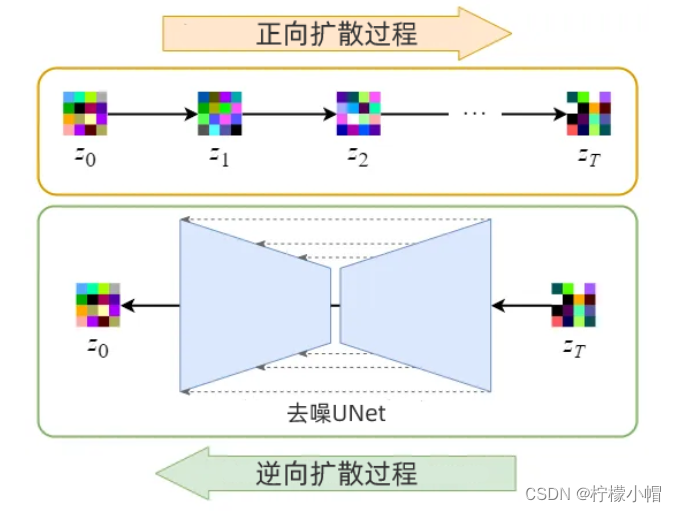
3.2 扩散过程

Stable Diffusion正向、逆向扩散过程都是在潜空间中进行，由于潜空间维度较低，所以具有较快的扩散速度。正向扩散过程，不断向前潜空间中添加噪声；逆向扩散过程，是不断从潜空间中去除噪声的过程。

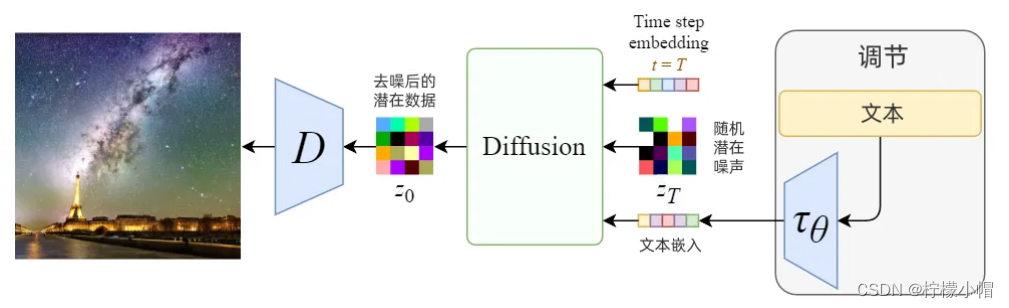
3.3 调节机制

Stable Diffusion是一个多模态模型，能实现文生图、图生图等功能。调节机制（Conditioning Mechanisms）是指，模型接收文本、图像或其它数据作为输入，作为条件或约束，生成符合该文本或图像描述的数据。如下图所示：

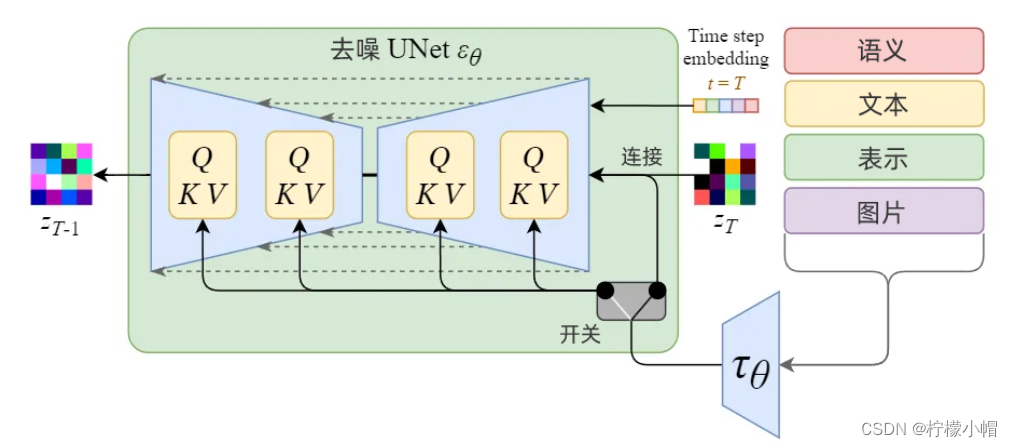
上图中，根据不同输入，分别做不同处理：

• 如果输入文本，经过语义模型${\tau }_{\theta }$转换为词嵌入表示，然后通过多头注意力Attension(Q, K, V)映射到U-Net层；
• 如果输入图片或其它语义表示，使用连接完成调节。

3.4 目标函数

Stable Diffusion的目标函数和扩散模型非常相似，不同点主要有两处：（1）输入潜在数据$z_t$而不是原图像$x_t$；（2）向U-Net中添加了调节输入${\tau }_{\theta }(y)$，表达式如下所示：

$$L_{LDT}={\mathbb{E}}_{t,z0,ϵ,y}[||ϵ-{ϵ}_{\theta }(z_t,t,{\tau }_{\theta }(y))|{|}^2]$$

其中，$z_t={\bar{\alpha }}_t+1-{\bar{\alpha }}_tϵ,z_0=E(x_0);{\tau }_{\theta }(y)$是输入调节。

3.5 Diffusion和Stable Diffusion的比较

1）Diffusion在图像空间进行扩散计算，Stable Diffusion在低维度的潜空间上进行扩散计算，所以后者更快

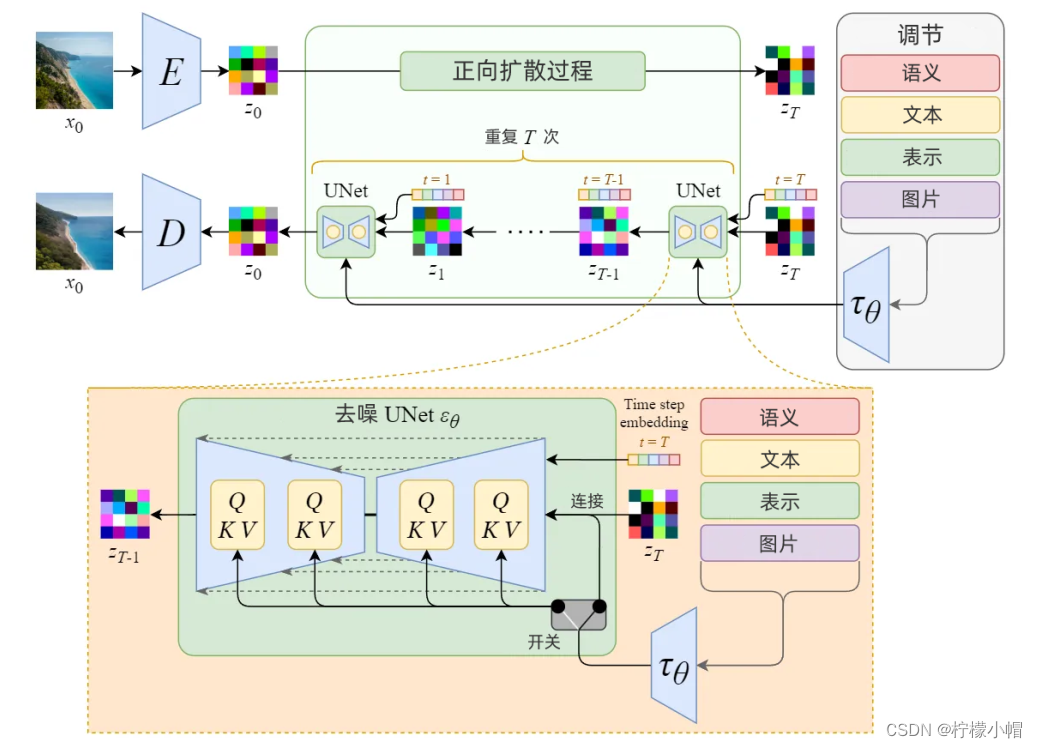
2）Stable Diffusion接收条件输入，是多模态模型，能根据文生图、图生图，应用更广泛。

3.6 实验

在线演示案例：https://huggingface.co/spaces/stabilityai/stable-diffusion