文章目录

摘要
创建逼真的虚拟世界需要对各种对象的 3D 表面几何体进行精确建模。为此,网格很有吸引力,因为它们 1) 使用逼真的材质和照明实现基于物理的快速渲染,2) 支持物理模拟,以及 3) 对于现代图形管道来说非常节省内存。然而,最近关于重建和统计建模 3D 形状的工作批评网格在拓扑上不灵活。为了捕获各种物体形状,任何 3D 表示都必须能够对固体、水密形状以及薄而开放的表面进行建模。最近的工作集中在前者上,重建开放表面的方法不支持使用材料和照明或无条件生成建模进行快速重建。受到开放表面可以被视为漂浮在水密表面上的岛屿的观察的启发,我们通过在水密模板上定义流形有符号距离场来参数化开放表面。通过这种参数化,我们进一步开发了一种基于网格的可微分表示,该表示对任意拓扑的水密和非水密网格进行参数化。我们的新表示称为 Ghost-on-the-Shell (G-SHELL),支持两个重要的应用:从多视图图像进行基于可微分光栅化的重建和非水密网格的生成建模。我们实证证明,G-SHELL 在非水密网格重建和生成任务上实现了最先进的性能,同时对水密网格也有效执行。
引言
创建高保真 3D 虚拟世界需要 3D 形状的表示,该表示可以高效、逼真地进行渲染和模拟。最常见的是,3D 形状表示为现代图形管道经过高度优化的网格。由于手动创建 3D 网格资产非常耗时,因此研究主要集中在从图像或生成模型自动创建。虽然最近的大部分工作都集中在水密网格上 [55, 56, 60, 67],许多 3D 对象(如衣服、纸张或树叶)是非水密的、开放的1 和薄的。此类表面的捕获和生成建模相对未得到充分探索。
现有的非水密网格建模方法通常会构建一个无符号距离场 (UDF) [35, 38],即 3D 坐标到最近表面的绝对距离的标量场。使用 UDF,可以通过提取和离散零 UDF 水平集来获得非水密网格。然而,与有符号距离场 (SDF) 相比,从 UDF 中提取等值面是一项艰巨的任务:Marching Cubes [39] 等经典算法中的等分搜索策略并不仅仅适用于 UDF。常见的解决方法包括 1) 后处理双层水密网格 [48, 70],引入局部伪符号进行二分搜索 [15],以及使用隐式无点到网格重建方法 [10]。这些方法不可避免地会引入建模误差,对非水密网格重建和生成构成挑战。
我们采用不同的方法来模拟非水密网格,具有以下关键观察结果:大多数开放表面可以被视为漂浮在水密表面上的实体,类似于漂浮在地球表面的大陆。换句话说,在某个水密表面模板上对开放表面边界进行建模就足够了。为了正式化这个想法,我们在水密模板上定义了一个流形有符号距离场 (mSDF),其中符号表示点是否位于开放表面,绝对比例表示到边界的测地线距离。现在可以通过使用 mSDF 的等值线提取来提取开放表面。
我们遵循这个直觉,设计了一个通用表示,Ghost-on-the-Shell(称为 G-SHELL),它共同参数化了水密模板和生活在其上的非水密网格。具体来说,我们将 3D 空间离散为单元网格,其中顶点存储 SDF 和 mSDF 值,然后应用类似 Marching-Cube 的提取来获得 SDF 等值面和 mSDF 等值线。我们的实现利用了一种高效的网格提取算法,而不是遵循 “等值面到等值线” 的天真两阶段方法。简而言之,我们在类似 Marching-Cube 的算法中调整了查找表,该算法根据 SDF 和 mSDF 符号枚举了每个单元中等值面的所有可能配置。这种实现有效地减少了创建的网格面的数量,从而减少了网格到网格映射的计算成本。
由于 G-SHELL 仅使用简单、确定性和可并行化的作进行网格提取,因此基于网格的逆向渲染现在可以应用于非水密网格,因为优化景观表现良好(使用简单的类似 Marching-Cube 的提取)和内存友好的计算(使用高效的网格光栅器)。这种高效的网格光栅化意味着我们现在能够通过利用基于物理的网格渲染来优化像素信息的材质和照明。此外,G-SHELL 的规则网格结构首次允许将最新的生成方法(例如扩散模型)扩展到非水密网格。
总括而言,我们的主要贡献如下:
网格表示。G-SHELL 是一种可微表示,可有效地参数化不同形状拓扑的水密和非水密网格。
效率。通过为 G-SHELL 设计的网格提取算法,我们实现了使用可微分光栅器快速重建非水密网格。具体来说,我们为 G-SHELL 设计了一种高效的网格提取算法。
基于物理的反向渲染。G-SHELL 支持水密和非水密网格的拓扑、材质和光照的联合优化。
网格生成。G-SHELL 的网格参数化和高效网格提取支持使用扩散模型对水密和非水密网格进行有效的生成建模。
我们将 G-SHELL 与当前流行的 3D 表示进行了定性和定量比较,以从逼真图像重建以及无条件生成水密和非水密网格,证明了 G-SHELL 在表示一般 3D 形状方面的优越性。
2 相关工作
网格参数化和提取。在现代计算机图形管道和软件中,3D 网格是关键的基础表示。网格重建的方法主要可以分为三类:从网格模板、从点云和从隐式领域。网格模板能够优化顶点位置以与对象表面对齐,但对于不同的拓扑结构来说可能是不灵活的 [16, 64]。一些方法 [45, 59, 61] 利用重新网格划分 [5, 20] 来适应拓扑变化,但仔细初始化仍然是必不可少的,以避免在优化过程中出现不良的局部最小值。与网格模板相比,点云可以直接从 Lidar 扫描中获得,同时为捕获各种形状拓扑提供了灵活性。这种灵活性的代价是推断点连通性的挑战 - 两个点在目标表面上是否彼此相邻。从点云构建表面的常用方法,如 Ball-Pivoting [3] 和 Delaunay Triangulation [28],不仅由于不可并行化作而速度慢,而且容易受到源点云中的噪声的影响。
因此,从隐式场中提取网格更为常见,隐式场可能是从泊松重建的点云 [24, 46, 54] 或多视图图像 [41, 67] 构建的。随后,可以通过使用 Marching Cubes [39]、Marching Tetrahedra [58] 和 Dual Contouring [23] 等方法识别和三角化零水平集来提取网格。其中许多算法是可微分的,例如 Deep Marching Cubes [30]、Neural Dual Contouring [9]、MeshSDF [49]、DMTet [55] 和 FlexiCubes [56]。但是,由于使用了 SDF,它们中的大多数仅适用于水密网格。为了处理非水密网格,一些论文提出了使用 UDF 的可微分方法。例如,MeshUDF [15] 计算网格顶点上的伪符号 —— 网格顶点上 UDF 渐变之间的内积符号 —— 并重用行进立方体从生成的伪 SDF 中提取网格。这些方法对输入噪声很敏感,因为从非负场中定位零电平集具有挑战性。虽然存在 UDF 以外的隐式表示,例如广义绕组编号 [2, 11, 21] 和 DeepCurrents [44] 的变体,但它们没有有效的可微分网格参数化。相比之下,我们的方法通过以类似 Marching-Cube 的方式提取零水平集,稳健而有效地模拟了非水密网格。
可微分逆向渲染。近年来,通过隐式表示进行可微逆渲染很流行,例如 NeRF [41] 和 SDF [60, 67],人们可以使用可微体积渲染 [37, 41] 或表面渲染 [22, 32, 67] 方法。这些方法适用于使用 UDF(例如 NeuralUDF [38]、NeUDF [35])和 SDF(例如 NeAT [40])重建非水密表面。但是,使用隐式表示进行渲染通常需要对渲染图像中的每个像素进行多次且可能昂贵的查询。由于几何体和颜色是以隐式方式编码的,因此在反向渲染过程中解开几何体、材质和照明相对困难。相比之下,显式表示,如点云和网格,可以通过光栅化 [25, 33] 有效地渲染,并允许轻松解开物理属性 [17, 34, 42]。与非水密网格建模的隐式方法相比,我们的方法利用基于网格的光栅化来实现多视图图像中形状、材料和照明的快速联合优化。
几何的生成建模。3D 生成被广泛研究用于各种表示,包括网格 [12, 13, 36, 43]、点云 [65, 68]、体素 [62] 等显式表示,以及有符号距离函数 (SDF) [6, 69] 和神经辐射场 (NeRF) [6, 7, 26, 53] 等隐式表示。然而,除了少数基于网格的方法外,所有其他方法都不会直接生成具有任意拓扑的网格。因此,通常必须执行额外的后处理步骤来提取网格,这可能非常耗时,并且可能会引入额外的错误。
最近,已经提出了使用中间网格表示生成网格的方法,要么通过直接 3D 建模 [12, 13, 36] 或通过从 2D 生成模型中提取信息 [8, 31]。虽然这些方法在生成水密 3D 网格方面取得了成功,但它们都无法生成非水密网格。也可以以自回归的方式直接生成网格:例如,PolyGen [43] 构建了一个基于变压器的自回归模型来交替生成顶点和边。然而,自回归模型可以非常灵活,以至于它们几乎无法扩展到具有非常密集的顶点集的复杂网格(尤其是那些不是由设计师创建的网格),并且经常产生自相交网格。相反,我们的方法能够生成具有精细几何细节且没有自相交的水密和非水密网格。
3 前提:基于 SDF 的网格提取
我们简要总结了 Marching Cubes,一种基于 SDF 的经典网格提取方法,并介绍了它的一些变体。简而言之,Marching Cubes 使用 3D 立方体网格离散 3D 空间,并使用简单的线性假设从每个立方体单元中提取面:每个单元中任何点的 SDF 值都是单元角上点的重心插值。具体来说,给定一个有 8 个角的单元格 ( p 1 , p 2 , . . . , p 8 ) (p_{1}, p_{2}, ..., p_{8}) (p1,p2,...,p8) ,我们首先得到重心坐标 ( c 1 , c 2 , . . . , c 8 ) (c_{1}, c_{2}, ..., c_{8}) (c1,c2,...,c8) 使得 x = ∑ i c i p i x=\sum_{i} c_{i} p_{i} x=∑icipi 。在线性假设下,提取的网格必须是多边形,其顶点位于立方单元边缘上。因此,用 SDF 值 s i < 0 < s j s_{i}<0<s_{j} si<0<sj 分别计算每条边上的网格顶点位置 ( p i , p j ) (p_{i}, p_{j}) (pi,pj) 就足够了。顶点位置只是 p i p_{i} pi 和 p j : u = ( s i p j − s j p i ) / ( s i − s j ) p_{j}: u=(s_{i} p_{j}-s_{j} p_{i}) /(s_{i}-s_{j}) pj:u=(sipj−sjpi)/(si−sj) 之间的线性插值。
这些提取的网格顶点的连通性可以通过查找表有效地推断出来。人们可以改用四面体网格,从而产生称为行进四面体的变体,为此,我们在图 2 中可视化了查找表。由于顶点是通过简单的可微分运算计算的,因此可以使用可能可变形的 SDF 值网格( e . g e.g e.g)、深行进立方体(有一些松弛)[30] 和 DMTet [55] 来参数化水密网格。

图 2:行进四面体的查找表(直到旋转对称)。带红点和不带红点的栅格折点都具有相反符号的 SDF 值。
4 G 壳:一般 3D 形状的富有表现力的表示
4.1 生活在水密表面上的开放表面
我们从以下对一类开放表面的简单观察开始,这将指导我们了解参数化具有位于水密表面上的开放表面的一般 3D 形状。
任何平滑且简单连接的开放曲面都可以平滑变形,成为球体的子集。
这是经典曲面拓扑理论的直接结果,附录 A 中给出了更多的数学细节。事实上,通过首先收缩孔,然后将其变形成球体,可以将大量表面(例如普通 T 恤)完成为水密表面。受这一观察结果的启发,我们在模板球体 M 上定义了一个连续且可微分的映射 ν : M → R \nu: M \to \mathbb{R} ν:M→R,以表征一个点是否属于开放表面 M 0 M_{0} M0
编号:
ν ( x ) > 0 , ∀ x ∈ I n t e r i o r ( M o ) ⏟ C a s e 1 : i n s i d e t h e o p e n s u r f a c e , ν ( x ) = 0 , ∀ x ∈ ∂ M o ⏟ C a s e 2 : o n t h e s u r f a c e b o u n d a r y ν ( x ) < 0 , O t h e r w i s e , ⏟ C a s e 3 : o u t s i d e t h e o p e n s u r f a c e \underbrace{\nu(x)>0, \forall x \in Interior\left(\mathcal{M}_{o}\right)}_{Case 1: inside the open surface }, \underbrace{\nu(x)=0, \forall x \in \partial \mathcal{M}_{o}}_{Case 2: on the surface boundary } \underbrace{\nu(x)<0, Otherwise, }_{Case 3: outside the open surface } Case1:insidetheopensurface
ν(x)>0,∀x∈Interior(Mo),Case2:onthesurfaceboundary
ν(x)=0,∀x∈∂MoCase3:outsidetheopensurface
ν(x)<0,Otherwise,
其中 ν 可以实例化为到位于水密模板上的开放表面边界的有符号测地线距离。虽然给定一些 M 和 M 0 M_{0} M0 的选择数可以是无限的,在不失去通用性的情况下,我们将 2 个流形的场称为有符号距离场 (mSDF),因为它是在流形表面上定义的,并以类似于 SDF 的方式表征边界。
现在,该问题实际上可以简化为学习由零等值线 2 定义的“2D 网格”。正如零等值面上的 3D 网格可以通过深行进立方体中的 3D 立方体网格进行参数化一样,“2D 网格”(多边形曲线)也可以通过“2D " 2 D "2D "2D 网格”、 i . e . i.e. i.e. 参数化,用于(变形的)球体的网格:只需学习 24 24 24 值在每个球体网格顶点上,我们从中提取非水密网格。此过程如图 3 所示。直观地说,一个开放的表面可以看作是 3D 壳体上切出空心真空后的剩余本质,因此我们将提出的 3D 表示命名为 Ghost-on-the-Shell2。

图 3:从一些水密三角网格中提取非水密网格的图示。 p 1 p_{1} p1 , p 2 p_{2} p2 是(水密)网格顶点的位置。 Δ p = ∥ p 1 − p 2 ∥ \Delta p=\left\|p_{1}-p_{2}\right\| Δp=∥p1−p2∥ 和 ν 1 > 0 > ν 2 \nu_{1}>0>\nu_{2} ν1>0>ν2 是相应的 mSDF 值。提取橙色三角形,丢弃蓝色多边形。
然而,这种幼稚的结构在应用于一般对象时会带来建模挑战。首先,它无法捕获与球体同胚的非同态表面(例如,甜甜圈)。此外,表面在 3D 中的一些简单变形可能会导致自相交,因此需要额外的正则化和/或建模技术来解决这个问题。

图 4:四面体网格的 G-SHELL 查找表(最高旋转对称)。带红点和不带红点的栅格顶点具有相反符号的 SDF 值,水密网格顶点上的绿点表示负 mSDF 值。粉红色区域表示最终提取的面,而蓝色区域是水密模板网格上的丢弃区域。除三角形以外的彩色多边形将沿虚线剪切。
4.2 使用 G-SHELL 进行高效网格提取
将 SDF 和 mSDF 值存储在同一个 3D 网格中,我们为 G-SHELL 获得了一种高效的类似 Marching-Cube 的算法,该算法重用了插值系数(公式 3)进行 mSDF 符号计算。具体来说,以边 ( p i , p j ) (p_{i}, p_{j}) (pi,pj) ,对应的 SDF 值 s i < 0 < s j s_{i}<0<s_{j} si<0<sj 和 mSDF 值 ν i \nu_{i} νi , ν j \nu_{j} νj ,我们可以计算提取的网格顶点上的 mSDF 值为 ν ′ = \nu'= ν′= ( s i ν j − s j ν i ) / ( s i − s j ) (s_{i} \nu_{j}-s_{j} \nu_{i}) /(s_{i}-s_{j}) (siνj−sjνi)/(si−sj) 。我们在图 4 中给出了四面体网格的查找表示例,该表列举了 SDF 符号(在网格顶点上)和 mSDF 符号(在水密网格顶点上)的所有可能情况。尽管以四面体网格为例,但我们注意到 G-SHELL 通常适用于其他网格结构,不仅限于四面体网格。
5 G-SHELL 的应用
5.1 从 MULTIVIEW 图像重建网格
借助 G-SHELL,现有的基于可微分光栅化的渲染方法(例如 [17, 42])可以无缝地应用于从多视图 RGB 和二进制掩码图像中端到端重建 3D 水密和非水密网格。使用光栅化进行重建不仅可以在没有姿势处理的情况下显式优化最终几何体,而且与使用 UDF 的体积渲染相比,还可以节省内存和时间 [35, 38] - 不再需要评估每条光线的多个采样点的密度。此外,通过基于物理的网格渲染,可以在单个阶段中共同优化几何体、材质和照明。
然而,我们注意到从图像中重建非水密网格时存在一些特别的困难。与永远无法看到内表面的水密网格不同,非水密表面有两面,一侧可能比另一侧更明显。例如,长裙的内部可能无法完全观察,而且当实际看到时,它也很可能光线不足。同样,间接照明必须与逼真的材质(尤其是高度镜面反射的材质)和潜在的复杂几何体一起考虑。为了简化问题,同时仍然能够证明 G-SHELL 表示的有效性,我们使用了 Nvdiffrecmc [17],这是一种遮挡感知的可微分渲染器,它忽略间接照明但考虑阴影光线。
另一个技术挑战是如何仅用 2D 图像识别拓扑孔的存在和位置,尤其是在只有有限数量的视图可用时。因此,我们建议通过引入“开孔”损失来正则化重建网格的 mSDF 值(mSDF 由具有一些参数集 θ m S D F \theta_{mSDF} θmSDF 的函数参数化):
L m S D F − r e g ( θ m S D F ) = ∑ u : ν θ m S T F ( u ) ≥ 0 L h u b e r ( ν θ m S D F ( u ) ) ⏟ E n c o u r a g e h o l e o p e n i n g + τ ⋅ ∑ u ′ : ν θ m N e w ( u ′ ) = 0 u ′ v i s i b l e f r o m s o m e q ∈ Q L h u b e r ( ν θ m S D F ( u ′ ) − ϵ ) ⏟ U ′ v i s i b l e f r o m s o m e q ∈ Q L R e g u l i x i r e l e s f o b l e n g t o l a r g e L_{mSDF-reg }\left(\theta_{mSDF}\right)=\underbrace{\sum_{u: \nu_{\theta_{mSTF}}(u) \geq 0} L_{huber }\left(\nu_{\theta_{mSDF}}(u)\right)}_{Encourage hole opening }+\underbrace{\tau \cdot \sum_{\substack{u': \nu_{\theta_{mNew}}\left(u'\right)=0 \\ u' visible from some q \in Q}} L_{huber }\left(\nu_{\theta_{mSDF}}\left(u'\right)-\epsilon\right)}_{U' visible from some q \in Q} L_{R e g u l i x i r e l e s f o b l e n g to large } LmSDF−reg(θmSDF)=Encourageholeopening u:νθmSTF(u)≥0∑Lhuber(νθmSDF(u))+U′visiblefromsomeq∈Q τ⋅u′:νθmNew(u′)=0u′visiblefromsomeq∈Q∑Lhuber(νθmSDF(u′)−ϵ)LRegulixirelesfoblengtolarge
其中 Q 是训练相机姿势的集合,T 和 ε 是一些正标量, L h u b e r L_{huber } Lhuber 是 Huber 损失函数。我们引入了第二个正则化项,以阻止拓扑空穴过大,尤其是在优化过程的早期阶段。我们在附录 B 中提供了有关剩余正则化损失和其他训练设置的所有详细信息。
5.2 G-MESHDIFFUSION:几何的生成建模
使用 G-SHELL 参数化的常规网格结构,可以直接训练生成模型以生成网格属性(SDF、mSDF 和潜在的网格变形),从而生成非水密网格。事实上,G-SHELL 支持使用扩散模型 [19] 进行生成建模,其中需要常规的输入结构。
为了演示 G-SHELL 的生成建模,我们考虑了 MeshDiffusion [36],它通过在 3D 四面体网格中对 SDF 和网格变形进行采样来生成水密网格,以生成非水密网格。虽然可以简单地在网格顶点属性上引入 mSDF 的附加维度,但生成的形状可能会产生噪声,如 [36] 中指出的那样。具体来说,生成的非水密网格的边界顶点是通过 mSDF 的插值来计算的:
u ′ = ∣ ν 1 ∣ ∣ ν 1 − ν 2 ∣ ⋅ u 2 − ∣ ν 2 ∣ ∣ ν 1 − ν 2 ∣ ⋅ u 1 , ν 1 < 0 < ν 2 , u'=\frac{\left|\nu_{1}\right|}{\left|\nu_{1}-\nu_{2}\right|} \cdot u_{2}-\frac{\left|\nu_{2}\right|}{\left|\nu_{1}-\nu_{2}\right|} \cdot u_{1}, \nu_{1}<0<\nu_{2}, u′=∣ν1−ν2∣∣ν1∣⋅u2−∣ν1−ν2∣∣ν2∣⋅u1,ν1<0<ν2,
其中 ( u 1 , u 2 ) (u_{1}, u_{2}) (u1,u2) 是提取的水密模板上的一条边,ν1、ν2 是相应的 mSDF 值。因为 ν i \nu_{i} νi 可以是任何实数,所以朴素的扩散损失会导致对 u ′ u' u′ 的加权预测不均匀。可以将 2 比 1 归一化,类似于 MeshDiffusion 对 SDF 值所做的作,但这是以牺牲表现力为代价的,因为网格变形已经用于补偿 SDF 值归一化产生的误差。
因此,我们提出了 MeshDiffusion 架构的修改版本来生成连续的 mSDF 值。具体来说,通过设置 α = ∣ ν 1 ∣ / ∣ ν 1 − ν 2 ∣ \alpha=|\nu_{1}| /|\nu_{1}-\nu_{2}| α=∣ν1∣/∣ν1−ν2∣ ,我们将方程 2 重写为 ( u 1 , u 2 ) (u_{1}, u_{2}) (u1,u2) : u ′ = α u 2 − ( 1 − α ) u 1 u'=\alpha u_{2}-(1-\alpha) u_{1} u′=αu2−(1−α)u1 的线性映射。因此,我们也可以生成线性插值系数 α,其界定在 [0, 1] 中。在 DMTet 中的四面体网格的情况下,每个单个单元中有 12 条候选边 ( u i , u j ) (u_{i}, u_{j}) (ui,uj),因为 u i ′ s u_{i} 's ui′s 始终位于四面体网格边缘上。我们只需将扩散模型设置为为每个单个单元格中的这些候选边生成所有 α ′ s \alpha 's α′s 。要使用的α最终根据每个生成的四面体单元的配置进行选择(如图 4 所示)。与 MeshDiffusion 类似,我们通过在 3D 对象的多视图数据集上运行逆向渲染来收集非水密网格数据集。我们将 G-SHELL 表示上的最终扩散模型称为 G -MeshDiffusion。更多详细信息可以在附录 C 中找到。
6 实验和结果
6.1 从多视角图像重建
基线。我们将我们的方法与当前最先进的非水密网格重建方法进行了比较:NeuralUDF [38]、NeUDF [35] 和 NeAT [40]。我们还评估了水密重建方法,包括 NeuS [60] 和 Nvdiffrecmc [17] (使用 DMTet [55])。我们遵循这些基线的原始设置,但对它们进行 400,000 次迭代的训练,掩码损失权重为 0.1。在测试期间,将呈现新视图,然后以 512 的分辨率进行评估。对于基于 UDF 的方法,非水密显式网格使用 MeshUDF [15] 提取,而对于基于 SDF 的方法 (NeuS/NeAT),网格使用具有相同分辨率的行进立方体 [39] 提取。对于带有 DMTet 的 Nvdiffrecmc,我们使用 128 的网格分辨率。
数据。我们使用 DeepFashion3D-v2 [18] 定量评估 G-SHELL 在非水密网格上的重建性能。具体来说,我们使用 9 个实例的 ground truth 网格与 [35, 38] 中使用的 DeepFashion3D-v1 实例重叠。与之前使用反照率图像进行训练和测试的工作(例如 NeuralUDF)不同,我们改用使用逼真的照明和阴影渲染的图像。具体来说,对于每个实例,我们使用带有 Cycles 引擎和真实环境光照贴图的 Blender 来渲染 72 个视图(RGB 图像和二进制分割掩码)用于训练,渲染 200 个视图用于测试。

图 5:在 DeepFashion3D 数据集上使用 G-SHELL 重建与其他基线方法进行多视图重建的比较。顶行:重建的纹理。底部 3 行:重建的网格。
| Method \ Instance ID | 30 | 92 | 117 | 133 | 164 | 320 | 448 | 522 | 591 | Avg |
|---|---|---|---|---|---|---|---|---|---|---|
| NeuS [ 60 ] | 31.876 | 26.850 | 29.234 | 29.692 | 30.405 | 33.827 | 31.591 | 32.846 | 26.282 | 30.289 |
| Nvdiffrecmc w/ DMTet [ 55 ] | 32.570 | 33.542 | 28.143 | 30.814 | 28.781 | 32.336 | 33.917 | 32.144 | 32.872 | 31.677 |
| NeuralUDF [ 38 ] | 30.264 | 25.887 | 28.908 | 31.115 | 28.463 | 30.739 | 32.185 | 29.965 | 32.574 | 30.011 |
| NeUDF [ 35 ] | 30.312 | 31.957 | 27.448 | 30.275 | 28.324 | 32.568 | 32.511 | 31.371 | 34.898 | 31.074 |
| NeAT [ 40 ] | 27.407 | 28.228 | 24.129 | 26.944 | 24.887 | 29.630 | 30.846 | 27.149 | 29.841 | 27.674 |
| Nvdiffrecmc w/ G-S HELL | 33.165 | 33.959 | 30.204 | 33.164 | 31.139 | 33.429 | 34.997 | 32.724 | 34.579 | 33.039 |
| Nvdiffrecmc w/ G-S HELL (FC) | 33.169 | 34.615 | 30.223 | 33.368 | 31.735 | 33.611 | 34.897 | 32.499 | 35.427 | 33.277 |
表 1:DeepFashion3D 服装实例上的 PSNR (↑)。标记:1 级和 2 级。
设置。对于使用 G-SHELL 的多视图重建,我们将四面体网格的网格分辨率设置为 128,将 FlexiCube 的网格分辨率设置为 80,并使用 2 个视图的批量大小训练 5000 次迭代的模型。对于所有基线方法,我们使用其论文中的默认设置。如果没有特别说明,我们的实验默认使用 G-SHELL 的四面体网格实现进行。为了证明 G-SHELL 的概念可以相当普遍,我们还评估了使用 FlexiCubes [56] 实现的 G-SHELL 的简单变体,在表 1 和表 2 中用 G-SHELL (FC) 表示。
重建质量。表 1 显示了所有测试视图的平均 PSNR。对于所有使用基于隐式的基线方法拟合的形状(即,除了带有 DMTet 的 Nvdiffrecmc),我们直接从学习的隐式场而不是提取的网格中渲染图像。我们还通过计算双向点云到网格倒角距离来评估所有方法对重建几何质量的影响。结果如表 2 所示,从中我们可以看到 G-SHELL 实现了出色的重建质量,并且优于许多最先进的方法。图 5 给出了定性比较,其中正面和背面网格面(重新定向以使其与相邻网格一致)涂有不同的颜色。图 6 中的定性结果表明,使用 FlexiCubes 的 G-SHELL 重建的网格拓扑比使用四面体网格的 G-SHELL 更规则,使其更适合物理仿真。更多结果见附录 F。
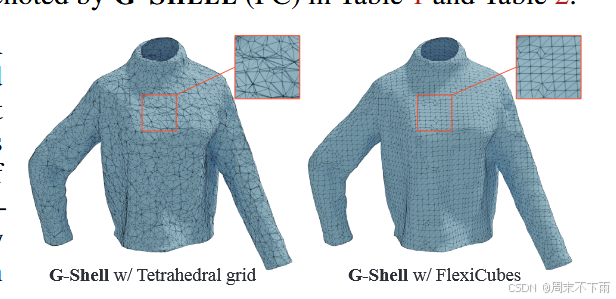
图 6:具有四面体网格的 G-SHELL 和具有 Flexicubes 的 G-SHELL 的重建网格拓扑。
| Method \ Instance ID | 30 | 92 | 117 | 133 | 164 | 320 | 448 | 522 | 591 | Avg |
|---|---|---|---|---|---|---|---|---|---|---|
| NeuS [60] | 0.450 | 1.244 | 0.505 | 0.709 | 0.528 | 0.426 | 0.734 | 0.598 | 1.737 | 0.770 |
| Nvdiffrernc w/ DMTet [55] | 0.629 | 0.466 | 0.724 | 0.856 | 0.722 | 0.444 | 0.444 | 0.649 | 1.026 | 0.662 |
| NeuralUDF [38] | 0.457 | 0.867 | 0.281 | 0.215 | 0.198 | 0.554 | 0.197 | 0.561 | 0.206 | 0.393 |
| NeUDF [35] | 0.315 | 0.458 | 0.204 | 0.107 | 0.184 | 0.432 | 0.159 | 0.585 | 0.128 | 0.286 |
| NeAT [40] | 0.605 | 0.325 | 1.010 | 0.873 | 0.538 | 0.305 | 0.323 | 0.591 | 0.237 | 0.534 |
| Nvdiffrernc w/ G-SHELL | 0.212 | 0.207 | 0.133 | 0.144 | 0.160 | 0.173 | 0.173 | 0.208 | 0.178 | 0.177 |
| Nvdiffrernc w/ G-SHELL (FC) | 0.235 | 0.227 | 0.146 | 0.154 | 0.165 | 0.229 | 0.195 | 0.261 | 0.234 | 0.203 |
表 2:DeepFashion3D 服装实例上的倒角距离 (cm ↓)。标记:1 级和 2 级。
| Method \ Metalness | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 | Avg |
|---|---|---|---|---|---|---|---|
| NeuS [60] | 33.59 | 32.03 | 31.62 | 31.21 | 30.58 | 30.45 | 31.58 |
| NeuralUDF [38] | 31.42 | 29.54 | 29.45 | 29.39 | 29.25 | 28.98 | 29.67 |
| NeUDF [35] | 32.45 | 29.32 | 29.04 | 29.19 | 29.13 | 29.18 | 29.72 |
| NeAT [40] | 28.41 | 27.37 | 28.07 | 26.93 | 26.58 | 26.85 | 27.37 |
| G-SHELL | 36.01 | 34.23 | 32.86 | 33.08 | 32.93 | 32.31 | 33.57 |
| Method \ Metalness | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 | Avg |
|---|---|---|---|---|---|---|---|
| NeuS [60] | 0.47 | 0.59 | 0.50 | 0.57 | 0.68 | 0.72 | 0.59 |
| NeuralUDF [38] | 0.51 | 1.06 | 1.05 | 0.98 | 0.53 | 0.85 | 0.83 |
| NeUDF [35] | 0.26 | 0.52 | 0.40 | 0.45 | 0.70 | 0.44 | 0.46 |
| NeAT [40] | 0.59 | 0.65 | 0.61 | 0.68 | 0.70 | 0.73 | 0.66 |
| G-SHELL | 0.20 | 0.22 | 0.28 | 0.24 | 0.24 | 0.27 | 0.24 |
表 3:金属材料的烧蚀研究。我们在实验中使用 Nvdiffrecmc 和提出的 G-SHELL 进行重建。上:PSNR (↑)。下:倒角距离 (cm ↓)。
从图 5 中,我们可以观察到,由于对照明、遮挡和材质的建模更好,我们的方法对新视图的预测比其他基线要好得多。由于服装内部的高度凹陷结构,我们还可以看到,在 DeepFashion3D 数据集中,水密重建基线往往无法重建服装的内侧。
训练和推理的效率。此外,我们还比较了所有非水密方法的运行时间(在具有单个 NVIDIA RTX 6000 GPU 的同一台计算机上进行测试)。与 Nvdiffrecmc 一起,G-SHELL 只需 3 小时即可拟合真值形状,而 NeuralUDF、NeUDF 和 NeAT 分别需要 17.3、16.4 和 4.3 小时。对于所有图像都以 512×512 的分辨率渲染的新视图合成,我们的方法以 2.7 秒/img 的速度运行(使用 Nvdiffrast 光栅器从学习的四面体网格推断 [27]),而 NeuralUDF、NeUDF 和 NeAT 分别以 1.8 min/img、1.4 min/img 和 9.7 min/img 运行。与其他方法相比,由于其高效的光栅化,我们的方法在训练和推理方面都明显更快。
6.2 混合水密和非水密网格重建
为了证明 G-SHELL 可以同时用于重建水密和非水密形状,我们在合成 NeRF 数据集 [41] 的一个实例上测试了我们的方法,其中所有图像都取自上方的物体,而不是下方的物体。我们采用一个极简主义假设,即看不见的区域应该始终为空,并使用 G-SHELL 重建目标形状。在图 7 的左侧,我们展示了目标形状的上表面得到了很好的重建,没有添加任何不必要的下表面面。在图 7 的右侧,我们还通过随机对表面附近的点进行采样来量化局部流形,从而可视化广义绕组数场 [2, 21]。它表明,使用 G-SHELL 进行逆向渲染可以重建水密和非水密部分的混合形状,其中只有可见上表面的区域被重建为单层网格。

图 7:左:重建的网格,背面涂成橙色。右:广义绕组编号字段;网格边界附近的点为白色。
6.3 镜面照明下的重建
网格反向渲染的一个关键优势是,在复杂的照明和材料的情况下,可以重建几何体。为了证明这种优势,我们进行了烧蚀实验,并比较了非水密网格重建方法在具有镜面表面的形状上的性能。具体来说,我们通过将粗糙度参数设置为 0.4 来修改图 5 中所示的毛衣网格的材料,并创建一组金属度参数范围为 0 到 1 的网格。我们对实验使用相同的超参数集。表 1 和表 3 中的结果验证了 G-SHELL 在复杂的照明和材料下可以很好地重建图像和形状。

图 8:G-MeshDiffusion 无条件生成的上衣和下衣样本。

表 4:所提出的 G-SHELL 扩散模型 (G-MeshDiffusion) 的定量结果。
6.4 生成式 3D 网格建模
基线。由于没有适用于流形结构的开放表面的网格生成模型,我们将我们的方法与两个水密网格生成模型进行了比较:MeshDiffusion [36] 和 GET3D [12],两者都使用基于 SDF 的 DMTet [55] 作为表示。详细的训练设置推迟到附录 C。在这个实验中,我们用四面体网格实现了 G-SHELL。
数据。我们从 Cloth3D 数据集 [4] 中收集了 4 个类别(T 恤、上衣、裙子、裤子)的网格,并将它们重新分为两个新类别:上衣(包括 T 恤和上衣)和下衣(包括裙子和裤子)。对于 MeshDiffusion(使用 DMTet 表示)G-MeshDiffusion(使用 G-SHELL 表示),我们使用 RGB、二进制掩码和深度监督在具有已知环境光照贴图和已知材质的网格上运行反向渲染。我们通常对 G-MeshDiffusion 遵循 [36] 的相同设置。对于 GET3D,我们遵循与 [12] 相同的训练设置,并渲染多视图 RGB 图像进行训练。
评估指标。对于每个模型,我们使用 100 步 DDIM [57] 对一组网格进行采样,其大小与测试集的大小相同,并将标准的拉普拉斯平滑应用于这些网格。与 [12, 36] 类似,我们评估从生成的网格中采样的点云与从真实网格中采样的点云之间的点云指标。为了弥补点云指标中感知测量的不足,我们还使用多视图 FID (MV-FID) [36, 69] 评估生成的结果,该结果由 20 个视图(使用固定光源渲染)的 FID(Fréchet Inception Distance)分数的平均值计算得出和仅漫反射网格材质)。在渲染过程中,我们不会将面法线重新定向到摄像机,以便可以考虑水密表面和开放表面之间的差异。

图 9:我们生成的样本的插值结果。

图 10:我们在训练集中生成的样本的最近邻。
定性和定量结果。定量结果见表 4。我们观察到,G-MeshDiffusion 通常比水密网格生成方法(MeshDiffusion 和 GET3D)具有更好的性能,但更重要的是,G-MeshDiffusion 可以更好地捕捉非水密网格的单面性质,因为它获得了明显更好的 MV-FID 分数。此外,我们在图 8 中定性地展示了来自 G-MeshDiffusion 的一些无条件采样网格。在 [36] 之后,我们还在图 9 中提供了一些插值序列(通过使用 100 步 DDIM 推理对初始高斯噪声进行球面线性插值获得)。插值结果显示了不同服装样式之间的平滑过渡。最后,我们在图 10 中展示了训练集中生成的网格的最近邻。结果表明,G-MeshDiffusion 不会记住训练样本,并且可以生成新的形状。
7 关于限制的讨论
表示法。G-SHELL 无法对具有自相交的形状进行建模。它也不对莫比乌斯带等不可定向的曲面进行建模,因为使用 SDF 意味着可定向性。此外,与分辨率可以被视为 “无限” 的隐式方法相比,G-SHELL 通常需要更高的分辨率才能对微小的拓扑孔进行建模。
网格重建。当目标几何体复杂时,网格渲染的不连续性会带来严重的优化问题,因为几何体和间接照明之间的纠缠会发挥作用。在本文中,我们只考虑了阴影光线,但在更复杂的场景中,可能需要对间接照明进行建模。
网格生成。3D U-Net 不节省内存,并且很难将它们缩放到高分辨率。使用 G-SHELL 进行更好的生成建模的未来工作可能包括更高效的架构,例如使用三平面特征的架构 [6],以及类似于 GET3D [12] 的替代 3D 生成方法。
8 结束语
我们提出的 G-SHELL 是一种通用的 3D 网格表示,它对水密和非水密网格进行建模。通过在具有不同拓扑结构的可学习水密网格模板上引入新的流形有符号距离场 (mSDF) 数量,我们实现了基于光栅化的重建和基于扩散模型的无条件生成非水密网格。这种设计可以在非水密网格建模中实现更好的性能和更大的灵活性。尽管如此,GSHELL 只能参数化有限的网格子集,尤其是在计算资源有限的情况下。此外,它还需要更好的反向渲染和生成建模技术,以充分利用 G-SHELL 的灵活性。
参考文献
[1] L.V. Ahlfors and L. Sario. Riemann Surfaces: (PMS-26). Princeton Mathematical Series. Princeton
University Press, 2015.
[2] Gavin Barill, Neil G Dickson, Ryan Schmidt, David IW Levin, and Alec Jacobson. Fast winding numbers
for soups and clouds. ACM Transactions on Graphics, 37(4):1–12, 2018.
[3] Fausto Bernardini, Joshua Mittleman, Holly Rushmeier, Cláudio Silva, and Gabriel Taubin. The ball-
pivoting algorithm for surface reconstruction. IEEE transactions on visualization and computer graphics,
5(4):349–359, 1999.
[4] Hugo Bertiche, Meysam Madadi, and Sergio Escalera. Cloth3d: clothed 3d humans. In ECCV, 2020.
[5] Mario Botsch and Leif Kobbelt. A remeshing approach to multiresolution modeling. In Eurographics,
2004.
[6] Eric R Chan, Connor Z Lin, Matthew A Chan, Koki Nagano, Boxiao Pan, Shalini De Mello, Orazio Gallo,
Leonidas J Guibas, Jonathan Tremblay, Sameh Khamis, et al. Efficient geometry-aware 3d generative
adversarial networks. In CVPR, 2022.
[7] Eric R Chan, Marco Monteiro, Petr Kellnhofer, Jiajun Wu, and Gordon Wetzstein. pi-gan: Periodic implicit
generative adversarial networks for 3d-aware image synthesis. In CVPR, 2021.
[8] Rui Chen, Yongwei Chen, Ningxin Jiao, and Kui Jia. Fantasia3d: Disentangling geometry and appearance
for high-quality text-to-3d content creation. In ICCV, 2023.
[9] Zhiqin Chen, Andrea Tagliasacchi, Thomas Funkhouser, and Hao Zhang. Neural dual contouring. ACM
Transactions on Graphics, 41(4), 2022.
[10] Julian Chibane, Gerard Pons-Moll, et al. Neural unsigned distance fields for implicit function learning. In
NeurIPS, 2020.
[11] Thor V Christiansen, Jakob Andreas Bærentzen, Rasmus R Paulsen, and Morten R Hannemose. Neural
representation of open surfaces. In Computer Graphics Forum, volume 42, page e14916. Wiley Online
Library, 2023.
[12] Jun Gao, Tianchang Shen, Zian Wang, Wenzheng Chen, Kangxue Yin, Daiqing Li, Or Litany, Zan Gojcic,
and Sanja Fidler. Get3d: A generative model of high quality 3d textured shapes learned from images. In
NeurIPS, 2022.
[13] William Gao, April Wang, Gal Metzer, Raymond A Yeh, and Rana Hanocka. Tetgan: A convolutional
neural network for tetrahedral mesh generation. In BMVC, 2022
[14] Amos Gropp, Lior Yariv, Niv Haim, Matan Atzmon, and Yaron Lipman. Implicit geometric regularization
for learning shapes. In ICML, 2020.
[15] Benoit Guillard, Federico Stella, and Pascal Fua. Meshudf: Fast and differentiable meshing of unsigned
distance field networks. In ECCV, 2022.
[16] Rana Hanocka, Gal Metzer, Raja Giryes, and Daniel Cohen-Or. Point2mesh: A self-prior for deformable
meshes. ACM Trans. Graph., 39(4), 2020.
[17] Jon Hasselgren, Nikolai Hofmann, and Jacob Munkberg. Shape, Light, and Material Decomposition from
Images using Monte Carlo Rendering and Denoising. In NeurIPS, 2022.
[18] Zhu Heming, Cao Yu, Jin Hang, Chen Weikai, Du Dong, Wang Zhangye, Cui Shuguang, and Han
Xiaoguang. Deep fashion3d: A dataset and benchmark for 3d garment reconstruction from single images.
In ECCV, 2020.
[19] Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. In NeurIPS, 2020.
[20] Jingwei Huang, Hao Su, and Leonidas Guibas. Robust watertight manifold surface generation method for
shapenet models. arXiv preprint arXiv:1802.01698, 2018.
[21] Alec Jacobson, Ladislav Kavan, and Olga Sorkine-Hornung. Robust inside-outside segmentation using
generalized winding numbers. ACM Transactions on Graphics, 32(4):1–12, 2013.
[22] Yue Jiang, Dantong Ji, Zhizhong Han, and Matthias Zwicker. Sdfdiff: Differentiable rendering of signed
distance fields for 3d shape optimization. In CVPR, 2020.
[23] Tao Ju, Frank Losasso, Scott Schaefer, and Joe Warren. Dual contouring of hermite data. In SIGGRAPH,
2002.
[24] Michael Kazhdan, Matthew Bolitho, and Hugues Hoppe. Poisson surface reconstruction. In SGP, 2006.
[25] Bernhard Kerbl, Georgios Kopanas, Thomas Leimkühler, and George Drettakis. 3d gaussian splatting for
real-time radiance field rendering. ACM Transactions on Graphics, 42(4):1–14, 2023.
[26] Adam R Kosiorek, Heiko Strathmann, Daniel Zoran, Pol Moreno, Rosalia Schneider, Sona Mokrá, and
Danilo Jimenez Rezende. Nerf-vae: A geometry aware 3d scene generative model. In ICML, 2021.
[27] Samuli Laine, Janne Hellsten, Tero Karras, Yeongho Seol, Jaakko Lehtinen, and Timo Aila. Modular
primitives for high-performance differentiable rendering. ACM Transactions on Graphics, 39(6):1–14,
2020.
[28] Der-Tsai Lee and Bruce J Schachter. Two algorithms for constructing a delaunay triangulation. Interna-
tional Journal of Computer & Information Sciences, 9(3):219–242, 1980.
[29] J. Lee. Introduction to Topological Manifolds. Graduate Texts in Mathematics. Springer New York, 2010.
[30] Yiyi Liao, Simon Donne, and Andreas Geiger. Deep marching cubes: Learning explicit surface representa-
tions. In CVPR, 2018.
[31] Chen-Hsuan Lin, Jun Gao, Luming Tang, Towaki Takikawa, Xiaohui Zeng, Xun Huang, Karsten Kreis,
Sanja Fidler, Ming-Yu Liu, and Tsung-Yi Lin. Magic3d: High-resolution text-to-3d content creation. In
CVPR, 2023.
[32] Shaohui Liu, Yinda Zhang, Songyou Peng, Boxin Shi, Marc Pollefeys, and Zhaopeng Cui. Dist: Rendering
deep implicit signed distance function with differentiable sphere tracing. In CVPR, 2020.
[33] Shichen Liu, Shunsuke Saito, Weikai Chen, and Hao Li. Learning to infer implicit surfaces without 3d
supervision. In NeurIPS, 2019.
[34] Weiyang Liu, Zhen Liu, Liam Paull, Adrian Weller, and Bernhard Schölkopf. Structural causal 3d
reconstruction. In ECCV, 2022.
[35] Yu-Tao Liu, Li Wang, Jie Yang, Weikai Chen, Xiaoxu Meng, Bo Yang, and Lin Gao. Neudf: Leaning
neural unsigned distance fields with volume rendering. In CVPR, 2023.
[36] Zhen Liu, Yao Feng, Michael J. Black, Derek Nowrouzezahrai, Liam Paull, and Weiyang Liu. Meshdiffu-
sion: Score-based generative 3d mesh modeling. In ICLR, 2023
[37] Stephen Lombardi, Tomas Simon, Jason Saragih, Gabriel Schwartz, Andreas Lehrmann, and Yaser Sheikh.
Neural volumes: learning dynamic renderable volumes from images. ACM Transactions on Graphics,
38(4):1–14, 2019.
[38] Xiaoxiao Long, Cheng Lin, Lingjie Liu, Yuan Liu, Peng Wang, Christian Theobalt, Taku Komura, and
Wenping Wang. Neuraludf: Learning unsigned distance fields for multi-view reconstruction of surfaces
with arbitrary topologies. In CVPR, 2023.
[39] William E Lorensen and Harvey E Cline. Marching cubes: A high resolution 3d surface construction
algorithm. In SIGGRAPH, 1987.
[40] Xiaoxu Meng, Weikai Chen, and Bo Yang. Neat: Learning neural implicit surfaces with arbitrary topologies
from multi-view images. In CVPR, 2023.
[41] Ben Mildenhall, Pratul P Srinivasan, Matthew Tancik, Jonathan T Barron, Ravi Ramamoorthi, and Ren Ng.
Nerf: Representing scenes as neural radiance fields for view synthesis. In ECCV, 2020.
[42] Jacob Munkberg, Jon Hasselgren, Tianchang Shen, Jun Gao, Wenzheng Chen, Alex Evans, Thomas
Mueller, and Sanja Fidler. Extracting Triangular 3D Models, Materials, and Lighting From Images. In
CVPR, 2022.
[43] Charlie Nash, Yaroslav Ganin, SM Ali Eslami, and Peter Battaglia. Polygen: An autoregressive generative
model of 3d meshes. In ICML, 2020.
[44] David Palmer, Dmitriy Smirnov, Stephanie Wang, Albert Chern, and Justin Solomon. Deepcurrents:
Learning implicit representations of shapes with boundaries. In CVPR, 2022.
[45] Junyi Pan, Xiaoguang Han, Weikai Chen, Jiapeng Tang, and Kui Jia. Deep mesh reconstruction from
single rgb images via topology modification networks. In ICCV, 2019.
[46] Songyou Peng, Chiyu Jiang, Yiyi Liao, Michael Niemeyer, Marc Pollefeys, and Andreas Geiger. Shape as
points: A differentiable poisson solver. In NeurIPS, 2021.
[47] Xuebin Qin, Hang Dai, Xiaobin Hu, Deng-Ping Fan, Ling Shao, and Luc Van Gool. Highly accurate
dichotomous image segmentation. In ECCV, 2022.
[48] Lingteng Qiu, Guanying Chen, Jiapeng Zhou, Mutian Xu, Junle Wang, and Xiaoguang Han. Rec-mv:
Reconstructing 3d dynamic cloth from monocular videos. In CVPR, 2023.
[49] Edoardo Remelli, Artem Lukoianov, Stephan Richter, Benoit Guillard, Timur Bagautdinov, Pierre Baque,
and Pascal Fua. Meshsdf: Differentiable iso-surface extraction. In NeurIPS, 2020.
[50] Ian Richards. On the classification of noncompact surfaces. Transactions of the American Mathematical
Society, 106(2):259–269, 1963.
[51] Johannes Lutz Schönberger and Jan-Michael Frahm. Structure-from-motion revisited. In CVPR, 2016.
[52] Johannes Lutz Schönberger, Enliang Zheng, Marc Pollefeys, and Jan-Michael Frahm. Pixelwise view
selection for unstructured multi-view stereo. In ECCV, 2016.
[53] Katja Schwarz, Yiyi Liao, Michael Niemeyer, and Andreas Geiger. Graf: Generative radiance fields for
3d-aware image synthesis. In NeurIPS, 2020.
[54] Silvia Sellán and Alec Jacobson. Stochastic poisson surface reconstruction. ACM Transactions on Graphics,
2022.
[55] Tianchang Shen, Jun Gao, Kangxue Yin, Ming-Yu Liu, and Sanja Fidler. Deep marching tetrahedra: a
hybrid representation for high-resolution 3d shape synthesis. In NeurIPS, 2021.
[56] Tianchang Shen, Jacob Munkberg, Jon Hasselgren, Kangxue Yin, Zian Wang, Wenzheng Chen, Zan
Gojcic, Sanja Fidler, Nicholas Sharp, and Jun Gao. Flexible isosurface extraction for gradient-based mesh
optimization. ACM Transactions on Graphics, 42(4):1–16, 2023.
[57] Jiaming Song, Chenlin Meng, and Stefano Ermon. Denoising diffusion implicit models. In ICLR, 2020.
[58] Graham M Treece, Richard W Prager, and Andrew H Gee. Regularised marching tetrahedra: improved
iso-surface extraction. Computers & Graphics, 23(4):583–598, 1999.
[59] Nanyang Wang, Yinda Zhang, Zhuwen Li, Yanwei Fu, Wei Liu, and Yu-Gang Jiang. Pixel2mesh:
Generating 3d mesh models from single rgb images. In ECCV, 2018.
[60] Peng Wang, Lingjie Liu, Yuan Liu, Christian Theobalt, Taku Komura, and Wenping Wang. Neus: Learning
neural implicit surfaces by volume rendering for multi-view reconstruction. NeurIPS, 2021.
[61] Xingkui Wei, Zhengqing Chen, Yanwei Fu, Zhaopeng Cui, and Yinda Zhang. Deep hybrid self-prior for
full 3d mesh generation. In ICCV, 2021.
[62] Jiajun Wu, Chengkai Zhang, Tianfan Xue, Bill Freeman, and Josh Tenenbaum. Learning a probabilistic
latent space of object shapes via 3d generative-adversarial modeling. In NIPS, 2016.
[63] Yuliang Xiu, Jinlong Yang, Xu Cao, Dimitrios Tzionas, and Michael J. Black. ECON: Explicit Clothed
humans Optimized via Normal integration. In CVPR, June 2023.
[64] Yuxuan Xue, Bharat Lal Bhatnagar, Riccardo Marin, Nikolaos Sarafianos, Yuanlu Xu, Gerard Pons-Moll,
and Tony Tung. Nsf: Neural surface fields for human modeling from monocular depth. In ICCV, 2023.
[65] Guandao Yang, Xun Huang, Zekun Hao, Ming-Yu Liu, Serge Belongie, and Bharath Hariharan. Pointflow:
3d point cloud generation with continuous normalizing flows. In ICCV, 2019.
[66] Guandao Yang, Abhijit Kundu, Leonidas J Guibas, Jonathan T Barron, and Ben Poole. Learning a diffusion
prior for nerfs. arXiv preprint arXiv:2304.14473, 2023.
[67] Lior Yariv, Yoni Kasten, Dror Moran, Meirav Galun, Matan Atzmon, Basri Ronen, and Yaron Lipman.
Multiview neural surface reconstruction by disentangling geometry and appearance. In NeurIPS, 2020.
[68] Xiaohui Zeng, Arash Vahdat, Francis Williams, Zan Gojcic, Or Litany, Sanja Fidler, and Karsten Kreis.
Lion: Latent point diffusion models for 3d shape generation. In NeurIPS, 2022.
[69] Xin-Yang Zheng, Yang Liu, Peng-Shuai Wang, and Xin Tong. Sdf-stylegan: Implicit sdf-based stylegan
for 3d shape generation. In SGP, 2022.
[70] Heming Zhu, Lingteng Qiu, Yuda Qiu, and Xiaoguang Han. Registering explicit to implicit: Towards
high-fidelity garment mesh reconstruction from single images. In CVPR, 2022.
节省内存空间、对于水密和非水密都有很好的效果。
提出一种全新的msdf,大大提升了非水密物体的重建质量。