目录
概述
TSP,也就是旅行商问题,是给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路的问题,而这个回路也称为最短哈密尔顿回路。
这是一个NP难问题,也就是到目前为止还没有确定出多项式级别复杂度算法的问题,不过不要紧,我们可以利用状压DP求解数据规模 n <= 20 的问题,这也是状压DP的主流应用之一。
标准TSP:最短哈密尔顿回路
AcWing 91:
给定一张 n 个点的带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数,其中第 i 行第 j 个整数表示点 i 到 j 的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤1e7输入样例:
5 0 2 4 5 1 2 0 6 5 3 4 6 0 8 3 5 5 8 0 5 1 3 3 5 0输出样例:
18
注意本题的要求是求解起点为0,终点为 n - 1 的e最短哈密尔顿回路,也就是没有严格成环。
算法过程
我们来思考如何定义dp数组。
状压DP,无疑是需要存储状态信息,也就是当前已经到访过的节点构成的二进制集合,第 i 位为1则代表节点 i 已经到访,例如:
19 = (10011),就代表0、1、4这三个节点已经到访(注意二进制位的下标从右向左递增)。
那我们还要存什么呢?考虑从一个状态转移到下一个状态的路径,还是刚才的例子:
(10011) -> (10111)
,节点3可能来自0、1、4这三个节点,因此我们还需要存储一个信息:当前站在哪个节点上,用于后续从这个节点进行转移。
于是定义dp[k][i],表示当前走过的节点由 k 的二进制状态表示,且此时站在 i 节点上的最短路。
初始条件下,k 等于1,即dp[(00...01)][0] = 0,表示站在0节点的初值,其余任意dp[k][i]为无穷大,表示未计算。
从 k = 2 开始枚举状态,对于每个 k ,枚举第 i 位是否为1(即 (k & (1 << i )) == 1)。
若第 i 位是1,则这是一个有效状态,k ^ (1 << i) 扣去第 i 位1得到前一个状态pre_k,在这个状态下枚举第 j 位 1,尝试从 pre_k 的第 j 位1转移到 k 的第 i 位1,也就是找到不包含 i 的节点集合pre_k,选其中一个点最优的抵达 i 。
转移方程 dp[k][i] = min(dp[k][i], dp[pre_k][j] + g[j][i]);
有两个细节:
由于合法状态必须从0节点开始走,所以任何0位不为1的 k 都不合法。
由于 k 从2开始,i 必不可能为0,因为不能从别的节点转移到0节点上,所以 i 从 1 开始枚举。
答案为dp[(1 << n) - 1][n - 1],(1 << n) - 1也即 n 位全1的状态,Code中称之为mx。
Code
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 20;
int g[N][N], dp[1 << N][N];
int n, mx;
int solve(){
memset(dp, 0x3f, sizeof(dp));
dp[1][0] = 0;
for (int k = 2; k <= mx; k++) if (k & 1)
for (int i = 1; i < n; i++) if (k & (1 << i)) {
int pre_k = k ^ (1 << i);
for (int j = 0; j < n; j++) if (pre_k & (1 << j))
dp[k][i] = min(dp[k][i], dp[pre_k][j] + g[j][i]);
}
return dp[mx][n - 1];
}
int main(){
cin >> n;
mx = (1 << n) - 1;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> g[i][j];
cout << solve();
return 0;
}复杂度
时间复杂度: O(n²
)
空间复杂度: O(n
)
扩展TSP:局部复重路径
LeetCode 847:
存在一个由
n个节点组成的无向连通图,图中的节点按从0到n - 1编号。给你一个数组
graph表示这个图。其中,graph[i]是一个列表,由所有与节点i直接相连的节点组成。返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止,也可以多次重访节点,并且可以重用边。
示例 1:
输入:graph = [[1,2,3],[0],[0],[0]] 输出:4 解释:一种可能的路径为 [1,0,2,0,3]
如果可以走回头路怎么办?
算法过程
我们来想一下回头路该怎么走。
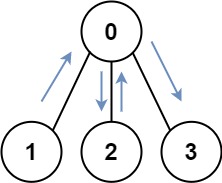
例如:
1 ← 0 → 2
↑ ← ↓对于dp[(111)][0],要从dp[(111)
][2]转移,注意到它们的二进制状态是相同的。
我把在状态 k 时,需要从相同状态转移的节点称为称为内部节点,反之,即符合标准TSP的节点称为外部节点。
一种思路是对于 k 的所有内部节点,都由 k 的外部节点作 BFS 求解。
但是这样太蠢了,甚至失去了状压的意义,因为可以直接 BFS 求解本题。
我们不妨换一个思路:从一个状态的某外部节点到下一个状态的某外部节点一定会有一条乃至多条最短路,他们会跨过内部节点。这些最短路是在一开始就确定的,如果直接用这些最短路一次转移到下个外部节点,就不用考虑一步一步地计算内部节点的更新了。
这样一来,问题就变回了标准TSP。
在这种想法下,我们可以直接预处理出最短路,使用Floyd最短路径算法求解全源最短路。
关于Floyd最短路径算法,请看图相关的文章。
Code
class Solution {
public:
int shortestPathLength(vector<vector<int>>& graph) {
const int n = graph.size(), mx = (1 << n) - 1;
vector g(n, vector(n, INT_MAX / 2));
for (int u = 0; u < n; u++)
for (int v : graph[u])
g[u][v] = g[v][u] = 1;
for (int k = 0; k < n; k++)
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++)
if (g[i][k] + g[k][j] < g[i][j])
g[i][j] = g[j][i] = g[i][k] + g[k][j];
vector dp(mx + 1, vector(n, 1ll * INT_MAX));
for (int i = 0; i < n; i++)
dp[1 << i][i] = 0;
for (int k = 1; k <= mx; k++)
for (int i = 0; i < n; i++) if(k & (1 << i)) {
int pre_k = k ^ (1 << i);
for (int j = 0; j < n; j++) if (pre_k & (1 << j))
dp[k][i] = min(dp[k][i], dp[pre_k][j] + g[i][j]);
}
return *min_element(dp[mx].begin(), dp[mx].end());
}
};复杂度
时间复杂度: O(n²
+ n³)
空间复杂度: O(n
+ n²)
路径追踪
LeetCode 943:
给定一个字符串数组
words,找到以words中每个字符串作为子字符串的最短字符串。如果有多个有效最短字符串满足题目条件,返回其中 任意一个 即可。我们可以假设
words中没有字符串是words中另一个字符串的子字符串。
示例 1:
输入:words = ["alex","loves","leetcode"] 输出:"alexlovesleetcode" 解释:"alex","loves","leetcode" 的所有排列都会被接受。示例 2:
输入:words = ["catg","ctaagt","gcta","ttca","atgcatc"] 输出:"gctaagttcatgcatc"
本质依然是TSP,但是要返回路径详细信息,怎么办?
算法过程
dp[k][i] 存储状态为 k ,后缀串为 i 的最短长度,计算和上面是相同的。
预处理出字符串 i 为前缀, j 为后缀的重叠长度 same[i][j],考虑没有字符串是另一个字符串的子字符串,因此 前缀 i 和后缀 j 必不重合,压缩时也不会发生跨越,same[i][j] 是合法的。
我们额外存储 from[k][i] ,表示 dp[k][i] 的来源。
初始状态 from[1 << i][i] = -1,单独的字符串 i 没有来源。
状态转移应该是这样的:
int new_dp = dp[pre_k][j] + words[i].size() - same[j][i];
if (new_dp < dp[k][i]){
dp[k][i] = new_dp;
from[k][i] = j;
}返回答案时,找到最短压缩串的后缀x,令 x 从后向前还原整条路径:
for (int mask = mx; mask; ) {
if (from[mask][x] != -1)
ans = words[x].substr(same[from[mask][x]][x]) + ans;
else
ans = words[x] + ans;
int pre_mask = mask;
mask ^= (1 << x);
x = from[pre_mask][x];
}Code
class Solution {
int dp[1 << 12][13], from[1 << 12][13];
int same[13][13];
string minstr(string& left, string& right){
if (left.empty()) return right;
else return left.size() <= right.size() ? left : right;
}
public:
string shortestSuperstring(vector<string>& words) {
const int n = words.size(), mx = (1 << n) - 1;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
string& a = words[i], b = words[j];
int l1 = a.length(), l2 = b.length(), len = min(l1, l2);
for (int k = len; k >= 1; k--)
if (a.substr(l1 - k) == b.substr(0, k)) {
same[i][j] = k;
break;
}
}
memset(dp, 0x3f, sizeof(dp));
for (int i = 0; i < n; i++) {
dp[1 << i][i] = words[i].size();
from[1 << i][i] = -1;
}
for (int k = 1; k <= mx; k++)
for (int i = 0; i < n; i++) if (k & (1 << i)) {
int pre_k = k ^ (1 << i);
for (int j = 0; j < n; j++) if (pre_k & (1 << j)) {
int new_dp = dp[pre_k][j] + words[i].size() - same[j][i];
if (new_dp < dp[k][i]){
dp[k][i] = new_dp;
from[k][i] = j;
}
}
}
string ans;
int x = 0;
for (int i = 1; i < n; i++)
if (dp[mx][x] > dp[mx][i])
x = i;
for (int mask = mx; mask; ) {
if (from[mask][x] != -1)
ans = words[x].substr(same[from[mask][x]][x]) + ans;
else
ans = words[x] + ans;
int pre_mask = mask;
mask ^= (1 << x);
x = from[pre_mask][x];
}
return ans;
}
};复杂度
时间复杂度: O(n²
+ n²m²) // m:单个字符串长度
空间复杂度: O(n
+ m²)
总结
燃尽了,这就是状压DP求解TSP必知必会的几个内容:从标准到泛化,从只输出结果到路径追踪,希望你有所收货。