『 C++ 入门到放弃』- 红黑树-EW帮帮网

1. 红黑树的概念

红⿊树是⼀棵⼆叉搜索树，他的每个结点增加⼀个数据来表⽰结点的颜⾊，可以是红⾊或者⿊⾊。通过对任何⼀条从根到叶⼦的路径上各个结点的颜⾊进⾏约束，红⿊树确保没有⼀条路径会⽐其他路径⻓出2倍，因⽽是接近平衡的

红黑树有以下几条规则

每个结点不是红⾊就是⿊⾊

根结点是⿊⾊的

如果⼀个结点是红⾊的，则它的两个孩⼦结点必须是⿊⾊的，也就是说任意⼀条路径不会有连续的
红⾊结点

对于任意⼀个结点，从该结点到其所有NULL结点的简单路径上，均包含相同数量的⿊⾊结点

2. 红黑树的实现

2.1 基本结构

// 枚举 => 用来表示一个节点是红还是黑
enum Color{
  RED,
  BLACK
};
// Node的结构 ( 以key/value 做演示 )
template<class K,class V>
  struct RBTNode{
    RBTNode(const K& key,const V& value):_left(nullptr),_right(nullptr),_parent(nullptr),_key(key),_value(value),_color(RED){}
    RBTNode<K,V>* _left;
    RBTNode<K,V>* _right;
    RBTNode<K,V>* _parent;
    K _key;
    V _value;
    Color _color;
  };
// 树的结构
template <class K, class V> class RBT {
  typedef RBTNode<K, V> Node;
  private:
  Node *_root = nullptr;
};

2.2 插入

红黑树的插入也需要针对不同情况作处理 => 插入一个新节点后不能破坏红黑树的性质

如果是空树插⼊，新增结点是⿊⾊结点；如果是⾮空树插⼊，新增结点必须红⾊结点，因为⾮空树插⼊，新增⿊⾊结点就破坏了规则4，规则4是很难维护的。
⾮空树插⼊后，新增结点必须红⾊结点，如果⽗亲结点是⿊⾊的，则没有违反任何规则，插⼊结束
⾮空树插⼊后，新增结点必须红⾊结点，如果⽗亲结点是红⾊的，则违反规则3 => 此时需要根据不同情况作处理

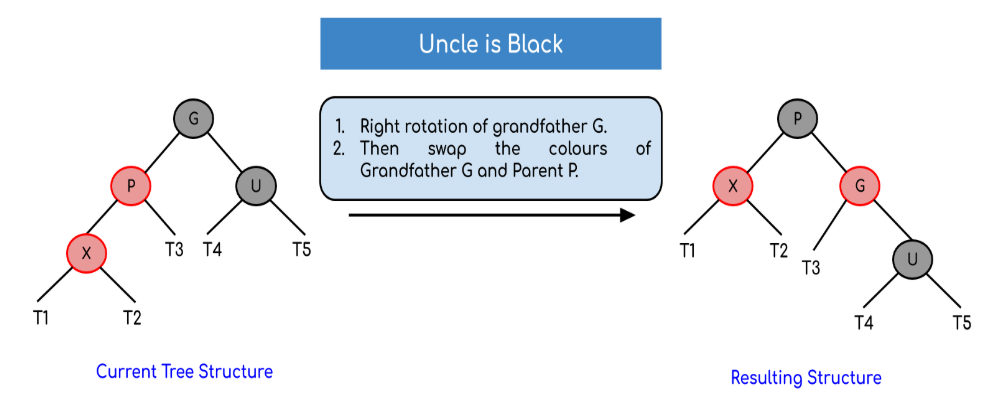
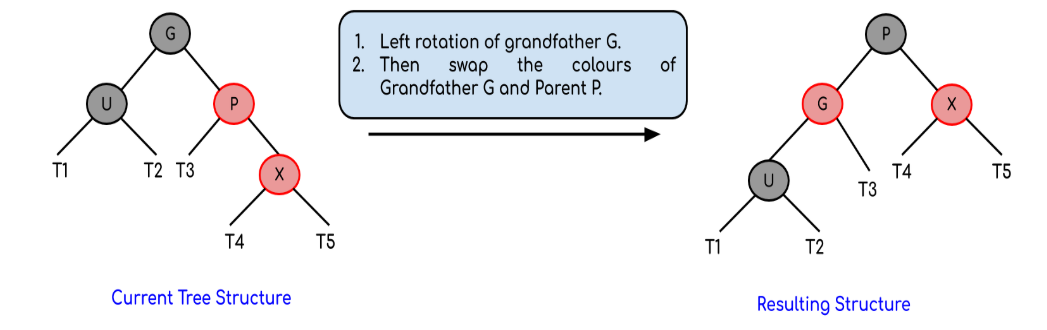
(1) 变色、不旋转 => 连续红节点且叔叔节点为红节点

旋转的特点为叔叔节点是黑节点

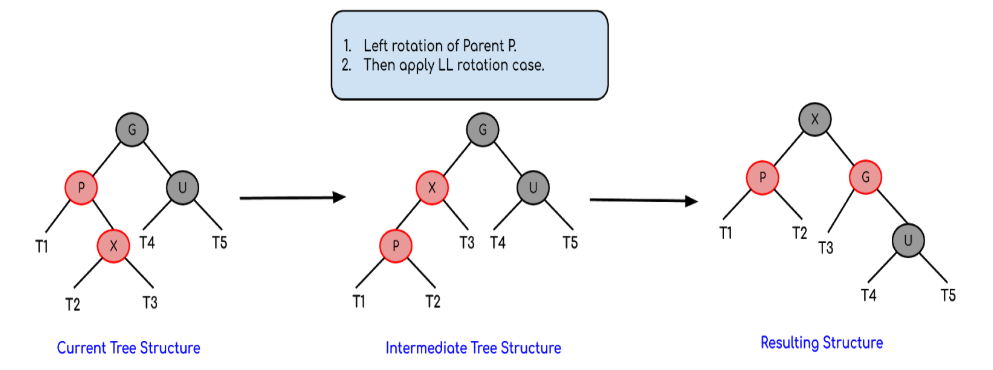
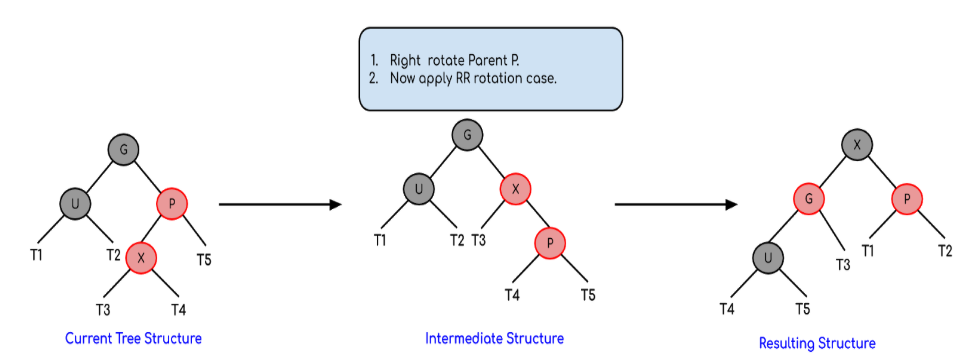
(2) 变色、单旋

//右旋逻辑 => 和AVL树是一样的，只是不用调整平衡因子
void RotateR(Node *parent) {
/*
 右旋的目标：
    1. 将parent的左子节点subL提升为新的根节点
    2. 将subL的右子节点subLR接到parent的左子节点位置
    3. 将parent接到subL的右子节点位置
    4. 更新所有相关的父节点指针，维护树的完整性
    */
  Node *subL = parent->_left; // 获取左子节点（将成为新的根节点）
  Node *subLR = subL->_right; // 获取左子节点的右子节点（需要重新接）

  // 步骤1：将subLR接到parent的左子节点位置
  parent->_left = subLR;
  if (subLR) {
    subLR->_parent = parent; // 更新subLR的父节点指针
  }
  // 步骤2：将parent接到subL的右子节点位置
  subL->_right = parent;
  // 步骤3：更新祖父节点的指向关系
  Node *parentParent = parent->_parent; // 获取祖父节点
  parent->_parent = subL;               // 更新parent的父节点指针
  if (parentParent == nullptr) {
    // 情况A：parent是根节点，subL成为新的根节点
    _root = subL;
    subL->_parent = nullptr; // 根节点没有父节点
  } else {
    // 情况B：parent不是根节点，需要更新祖父节点的指向
    if (parent == parentParent->_left) {
      parentParent->_left = subL; // parent原本是左子节点，subL也成为左子节点
    } else {
      parentParent->_right = subL; // parent原本是右子节点，subL也成为右子节点
    }
    subL->_parent = parentParent; // 更新subL的父节点指针
  }
}

// 左旋逻辑
void RotateL(Node *parent) {
  /*
    左旋的目标：
    1. 将parent的右子节点subR提升为新的根节点
    2. 将subR的左子节点subRL接到parent的右子节点位置
    3. 将parent接到subR的左子节点位置
    4. 更新所有相关的父节点指针，维护树的完整性
   */
  Node *subR = parent->_right; // 获取右子节点（将成为新的根节点）
  Node *subRL = subR->_left;   // 获取右子节点的左子节点（需要重新接）

  // 步骤1：将subRL接到parent的右子节点位置
  parent->_right = subRL;
  if (subRL) {
    subRL->_parent = parent; // 更新subRL的父节点指针
  }

  // 步骤2：将parent接到subR的左子节点位置
  subR->_left = parent;

  // 步骤3：更新祖父节点的指向关系
  Node *parentParent = parent->_parent; // 获取祖父节点
  parent->_parent = subR;               // 更新parent的父节点指针
  if (parentParent == nullptr) {
    // 情况A：parent是根节点，subR成为新的根节点
    _root = subR;
    subR->_parent = nullptr; // 根节点没有父节点
  } else {
    // 情况B：parent不是根节点，需要更新祖父节点的指向
    if (parent == parentParent->_right) {
      parentParent->_right = subR; // parent原本是右子节点，旋转后subR成为新的右子节点
    } else {
      parentParent->_left = subR; // parent原本是左子节点，旋转后subR成为新的左子节点
    }
    subR->_parent = parentParent; // 更新subR的父节点指针
  }
}

(3) 双旋、变色

bool insert(const pair<K, V> &kv) {
  // 1. 如果根节点为空，直接插入为根节点，并设为黑色
  if (_root == nullptr) {
    _root = new Node(kv);
    _root->_color = BLACK;
    return true;
  }
  // 2. 根节点不为空，寻找插入位置
  Node *parent = nullptr;
  Node *cur = _root;
  while (cur) {
    // 如果当前节点的key小于插入key，往右子树找
    if (cur->_kv.first < kv.first) {
      parent = cur;
      cur = cur->_right;
    } else if (cur->_kv.first >
               kv.first) { // 如果当前节点的key大于插入key，往左子树找
      parent = cur;
      cur = cur->_left;
    } else { // 如果已经存在相同key，不插入
      return false;
    }
  }
  // 2.2 插入新节点到找到的位置
  cur = new Node(kv);
  if (parent->_kv.first < kv.first) {
    parent->_right = cur;
  } else {
    parent->_left = cur;
  }
  cur->_parent = parent;
  // 2.3 插入后进行红黑树性质调整
  while (parent && parent->_color == RED) {
    Node *grandfather = parent->_parent; // 祖父节点
    // 情况1：父节点是祖父的左孩子
    if (grandfather->_left == parent) {
      Node *uncle = grandfather->_right; // 叔叔节点
      // 1.1 叔叔存在且为红色，进行颜色翻转
      if (uncle && uncle->_color == RED) {
        parent->_color = BLACK;
        uncle->_color = BLACK;
        grandfather->_color = RED;
        // 继续向上调整
        cur = grandfather;
        parent = cur->_parent;
      }
      // 1.2 叔叔不存在或为黑色，需要旋转
      else {
        // 当前节点是父节点的左孩子，右旋祖父
        if (cur == parent->_left) {
          RotateR(grandfather);
          parent->_color = BLACK;
          grandfather->_color = RED;
        } else { // 当前节点是父节点的右孩子，先左旋父节点再右旋祖父
          RotateL(parent);
          RotateR(grandfather);
          parent->_color = BLACK;
          grandfather->_color = RED;
        }
        break; // 调整完毕，跳出循环
      }
      // 情况2：叔叔不存在或为黑
    } else {
      Node *uncle = grandfather->_left; // 叔叔节点
      // 2.1 叔叔存在且为红
      if (uncle && uncle->_color == RED) {
        parent->_color = BLACK;
        uncle->_color = BLACK;
        grandfather->_color = RED;
        // 继续向上调整
        cur = grandfather;
        parent = cur->_parent;
      }
      // 2.2 叔叔不存在或为黑
      else {
        // 当前节点是父节点的右孩子，左旋祖父
        if (cur == parent->_right) {
          RotateL(grandfather);
          parent->_color = BLACK;
          
          grandfather->_color = RED;
        } else { // 当前节点是父节点的左孩子，先右旋父节点再左旋祖父
          RotateR(parent);
          RotateL(grandfather);
          parent->_color = BLACK;
          grandfather->_color = RED;
        }
        break; // 调整完毕，跳出循环
      }
    }
  }
  // 最后确保根节点为黑色
  _root->_color = BLACK;
  return true;
}

2.3 查找

Node *find(const K &key) {
  Node *cur = _root;
  while (cur) {
    if (cur->_kv.first < key) {
      cur = cur->_right;
    } else if (cur->_kv.first > key) {
      cur = cur->_left;
    } else {
      return cur;
    }
  }
  return nullptr;
}

2.4 判断红黑树是否平衡

// 检查红黑树是否满足所有性质
  // root: 当前检查的节点
  // blackNum: 当前路径经过的黑色节点数
  // refNum: 标准黑色节点数（根到最左叶子的黑色节点数）
  // 返回true表示满足红黑树性质
  bool Check(Node *root, int blackNum, const int refNum) {
    if (root == nullptr) {
      // 遍历到空节点，检查黑色节点数是否一致
      if (refNum != blackNum) {
        cout << "存在黑色结点的数量不相等的路径" << endl;
        return false;
      }
      return true;
    }
    // 检查是否有连续红色节点
    if (root->_color == RED && root->_parent->_color == RED) {
      cout << root->_kv.first << "存在连续的红色结点" << endl;
      return false;
    }
    if (root->_color == BLACK) {
      blackNum++;
    }
    return Check(root->_left, blackNum, refNum) &&
           Check(root->_right, blackNum, refNum);
  }

  // 判断红黑树是否平衡（即是否满足红黑树所有性质）
  bool IsBalance() {
    if (_root == nullptr) {
      return true;
    }
    if (_root->_color == RED) {
      cout << "根节点是红色" << endl;
      return false;
    }
    int refNum = 0;
    Node *left = _root;
    // 统计根到最左叶子的黑色节点数
    while (left) {
      if (left->_color == BLACK) {
        refNum++;
      }
      left = left->_left;
    }
    return Check(_root, 0, refNum);
  }

3. AVL树 vs. 红黑树

与红黑树相比，AVL 树更加平衡，但在插入和删除操作中可能需要更多旋转。因此，如果应用程序涉及频繁的插入和删除操作，则应优先选择红黑树。如果插入和删除操作较少，而搜索操作较为频繁，则应优先选择AVL 树而非红黑树。

此外，AVL树性质被破坏时一定会旋转，而红黑树不一定 ( 可能只是变色 )

4. set 和 map 的实现

set 和 map 的实现底层是用红黑树实现的，因此在这里也模拟实现

再模拟实现 set 和 map 前要先修改一下我们前面写的红黑树

enum Color { RED, BLACK };

// 红黑树节点结构体模板
// T：节点存储的数据类型（如 pair<K, V> 或自定义 struct）
// 设计原因：模板化节点类型，支持多种数据结构
template <class T> 
  struct RBTNode {
    // 构造函数，初始化数据并默认颜色为红色
    RBTNode(const T &data)
      : _left(nullptr), _right(nullptr), _parent(nullptr), _data(data),
    _color(RED) {}
    RBTNode<T> *_left;   
    RBTNode<T> *_right;  
    RBTNode<T> *_parent; 
    T _data;  // 节点存储的数据类型    
    Color _color;       
  };

// 红黑树迭代器模板
// T：节点数据类型，Ref/Ptr：引用和指针类型
template <class T, class Ref, class Ptr> 
  struct RBTreeIterator {
    typedef RBTNode<T> Node;
    typedef RBTreeIterator<T, Ref, Ptr> Self;
    Node *_node; // 当前迭代器指向的节点
    Node *_root; // 整棵树的根节点（用于--到end时定位最大节点）
    RBTreeIterator(Node *node, Node *root) : _node(node), _root(root) {}


    Ref operator*() { return _node->_data; }   // 解引用，返回节点数据
    Ptr operator->() { return &_node->_data; } // 指针访问
    // 前置++，移动到下一个节点（中序遍历）
    Self &operator++() {
      if (_node->_right) {
        Node *leftmost = _node->_right;
        while (leftmost->_left)
          leftmost = leftmost->_left;
        _node = leftmost;
      } else {
        Node *cur = _node, *parent = cur->_parent;
        while (parent && cur == parent->_right) {
          cur = parent;
          parent = parent->_parent;
        }
        _node = parent;
      }
      return *this;
    }
    // 前置--，移动到上一个节点（中序遍历）
    Self &operator--() {
      if (_node == nullptr) { // 如果为空 => 找最右边的节点
        Node *rightmost = _root;
        while (rightmost->_right)
          rightmost = rightmost->_right;
        _node = rightmost;
        // 如果左子树存在 => 找左子树的最右的节点
      } else if (_node->_left) {
        Node *rightmost = _node->_left;
        while (rightmost->_right)
          rightmost = rightmost->_right;
        _node = rightmost;
      } else {
        Node *cur = _node, *parent = cur->_parent;
        while (parent && cur == parent->_left) {
          cur = parent;
          parent = parent->_parent;
        }
        _node = parent;
      }
      return *this;
    }
    bool operator!=(const Self &s) const { return _node != s._node; }
    bool operator==(const Self &s) const { return _node == s._node; }
  };

// 红黑树主类模板
// K：键类型，T：节点数据类型，KeyOfT：仿函数，从T中提取K
// 设计原因：支持泛型键值类型，KeyOfT适配不同数据结构
template <class K, class T, class KeyOfT> class RBT {
  typedef RBTNode<T> Node;

  public:
  typedef RBTreeIterator<T, T &, T *> Iterator;
  typedef RBTreeIterator<T, const T &, const T *> ConstIterator;
  RBT() = default;

  // 返回最左节点的迭代器（begin）
  Iterator begin() {
    Node *leftmost = _root;
    while (leftmost && leftmost->_left)
      leftmost = leftmost->_left;
    return Iterator(leftmost, _root);
  }
  // 返回end迭代器（空节点）
  Iterator end() { return Iterator(nullptr, _root); }
  ConstIterator begin() const {
    Node *leftmost = _root;
    while (leftmost && leftmost->_left)
      leftmost = leftmost->_left;
    return ConstIterator(leftmost, _root);
  }
  ConstIterator end() const { return ConstIterator(nullptr, _root); }

  // 析构函数，递归释放所有节点
  ~RBT() {
    Destroy(_root);
    _root = nullptr;
  }

  // 插入数据，返回插入位置和是否插入成功
  // 设计思路：先查找插入位置，若已存在则返回已存在节点，否则插入并调整红黑树
  pair<Iterator, bool> insert(const T &data) {
    if (_root == nullptr) {
      _root = new Node(data);
      _root->_color = BLACK;
      return make_pair(Iterator(_root, _root), true);
    }
    KeyOfT kot;
    Node *parent = nullptr, *cur = _root;
    while (cur) {
      if (kot(cur->_data) < kot(data)) {
        parent = cur;
        cur = cur->_right;
      } else if (kot(cur->_data) > kot(data)) {
        parent = cur;
        cur = cur->_left;
      } else {
        // 已存在
        return make_pair(Iterator(cur, _root), false);
      }
    }
    cur = new Node(data);
    if (kot(parent->_data) < kot(data))
      parent->_right = cur;
    else
      parent->_left = cur;
    cur->_parent = parent;
    // 插入后调整红黑树性质
    while (parent && parent->_color == RED) {
      Node *grandfather = parent->_parent;
      if (grandfather->_left == parent) {
        Node *uncle = grandfather->_right;
        if (uncle && uncle->_color == RED) {
          parent->_color = BLACK;
          uncle->_color = BLACK;
          grandfather->_color = RED;
          cur = grandfather;
          parent = cur->_parent;
        } else {
          if (cur == parent->_left) {
            RotateR(grandfather);
            parent->_color = BLACK;
            grandfather->_color = RED;
          } else {
            RotateL(parent);
            RotateR(grandfather);
            parent->_color = BLACK;
            grandfather->_color = RED;
          }
          break;
        }
      } else {
        Node *uncle = grandfather->_left;
        if (uncle && uncle->_color == RED) {
          parent->_color = BLACK;
          uncle->_color = BLACK;
          grandfather->_color = RED;
          cur = grandfather;
          parent = cur->_parent;
        } else {
          if (cur == parent->_right) {
            RotateL(grandfather);
            parent->_color = BLACK;
            grandfather->_color = RED;
          } else {
            RotateR(parent);
            RotateL(grandfather);
            parent->_color = BLACK;
            grandfather->_color = RED;
          }
          break;
        }
      }
    }
    _root->_color = BLACK;
    return make_pair(Iterator(cur, _root), true);
  }

  // 查找数据，返回迭代器
  Iterator find(const T &data) {
    KeyOfT kot;
    Node *cur = _root;
    while (cur) {
      if (kot(cur->_data) < kot(data))
        cur = cur->_right;
      else if (kot(cur->_data) > kot(data))
        cur = cur->_left;
      else
        return Iterator(cur, _root);
    }
    return end();
  }

  // 检查红黑树是否满足所有性质
  bool Check(Node *root, int blackNum, const int refNum) {
    if (root == nullptr) {
      if (refNum != blackNum) {
        cout << "存在黑色节点数量不相等的路径" << endl;
        return false;
      }
      return true;
    }
    if (root->_color == RED && root->_parent && root->_parent->_color == RED) {
      cout << "存在连续的红色节点" << endl;
      return false;
    }
    if (root->_color == BLACK)
      blackNum++;
    return Check(root->_left, blackNum, refNum) &&
      Check(root->_right, blackNum, refNum);
  }

  // 判断红黑树是否平衡
  bool IsBalance() {
    if (_root == nullptr)
      return true;
    if (_root->_color == RED) {
      cout << "根节点是红色" << endl;
      return false;
    }
    int refNum = 0;
    Node *left = _root;
    while (left) {
      if (left->_color == BLACK)
        refNum++;
      left = left->_left;
    }
    return Check(_root, 0, refNum);
  }

  private:
  // 递归销毁所有节点
  void Destroy(Node *root) {
    if (root == nullptr)
      return;
    Destroy(root->_left);
    Destroy(root->_right);
    delete root;
  }
  Node *_root = nullptr; // 红黑树根节点

  // 右旋操作，维护红黑树平衡
  void RotateR(Node *parent) {
    Node *subL = parent->_left;
    Node *subLR = subL->_right;
    parent->_left = subLR;
    if (subLR)
      subLR->_parent = parent;
    subL->_right = parent;
    Node *parentParent = parent->_parent;
    parent->_parent = subL;
    if (parentParent == nullptr) {
      _root = subL;
      subL->_parent = nullptr;
    } else {
      if (parent == parentParent->_left)
        parentParent->_left = subL;
      else
        parentParent->_right = subL;
      subL->_parent = parentParent;
    }
  }

  // 左旋操作，维护红黑树平衡
  void RotateL(Node *parent) {
    Node *subR = parent->_right;
    Node *subRL = subR->_left;
    parent->_right = subRL;
    if (subRL)
      subRL->_parent = parent;
    subR->_left = parent;
    Node *parentParent = parent->_parent;
    parent->_parent = subR;
    if (parentParent == nullptr) {
      _root = subR;
      subR->_parent = nullptr;
    } else {
      if (parent == parentParent->_right)
        parentParent->_right = subR;
      else
        parentParent->_left = subR;
      subR->_parent = parentParent;
    }
  }
};

// myset.h
// 要include 红黑树的代码，再复用
template <class K> class set {
  // 仿函数，直接返回key本身
  // 设计原因：set的元素就是key，不需要从pair中提取d
  struct SetKeyOfT {
    const K &operator()(const K &key) { return key; }
  };

public:
  // 迭代器类型定义，直接复用RBT的迭代器
  typedef typename RBT<K, K, SetKeyOfT>::Iterator iterator;
  typedef typename RBT<K, K, SetKeyOfT>::ConstIterator const_iterator;

  // begin/end接口，支持范围for遍历
  iterator begin() { return _t.begin(); }
  iterator end() { return _t.end(); }
  const_iterator begin() const { return _t.begin(); }
  const_iterator end() const { return _t.end(); }

  // 插入元素，返回插入结果
  pair<iterator, bool> insert(const K &key) { return _t.insert(key); }
  // 查找元素，返回迭代器
  iterator find(const K &key) { return _t.find(key); }

private:
  RBT<K, K, SetKeyOfT> _t; // 底层用红黑树实现
};

// mymap.h

// map模板类，K为key类型，V为value类型
template <class K, class V> class map {
  // 仿函数，从pair<K, V>中提取key
  struct MapKeyOfT {
    const K &operator()(const pair<K, V> &kv) { return kv.first; }
  };

public:
  // 迭代器类型定义，复用RBT的迭代器
  typedef typename RBT<K, pair<const K, V>, MapKeyOfT>::Iterator iterator;
  typedef typename RBT<K, pair<const K, V>, MapKeyOfT>::ConstIterator
      const_iterator;

  iterator begin() { return _t.begin(); }
  iterator end() { return _t.end(); }
  const_iterator begin() const { return _t.begin(); }
  const_iterator end() const { return _t.end(); }

  // 下标操作符，若key不存在则插入默认值
  V &operator[](const K &key) {
    pair<iterator, bool> ret = insert(make_pair(key, V()));
    return ret.first->second;
  }

  // 插入键值对
  pair<iterator, bool> insert(const pair<K, V> &kv) { return _t.insert(kv); }
  // 查找key，返回迭代器
  iterator find(const K &key) { return _t.find(key); }

private:
  RBT<K, pair<K, V>, MapKeyOfT> _t; // 底层用红黑树实现
};

『 C++ 入门到放弃』- 红黑树

1. 红黑树的概念

2. 红黑树的实现

2.1 基本结构

2.2 插入

2.3 查找

2.4 判断红黑树是否平衡

3. AVL树 vs. 红黑树

4. set 和 map 的实现

网站公告

今日签到

热门文章

最新发布

『 C++ 入门到放弃 』- 红黑树

1. 红黑树的概念

2. 红黑树的实现

2.1 基本结构

2.2 插入

2.3 查找

2.4 判断红黑树是否平衡

3. AVL树 vs. 红黑树

4. set 和 map 的实现

网站公告

今日签到

热门文章

最新发布

『 C++ 入门到放弃』- 红黑树