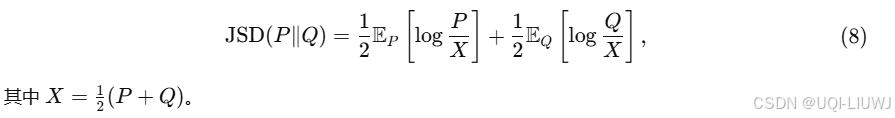Journal of Data Science 2021
1 intro
- 轨迹数据已被用于交通拥堵分析、出行模式与行为分析、个性化路线推荐等应用
- 然而,由于企业和个人对隐私保护的需求,获取大规模轨迹数据依然困难
- 因此,研究者致力于生成具备类似特征的新轨迹数据。
- 大多数序列轨迹合成模型侧重于预测人类或其他目标的移动轨迹。
- 以往研究中,如马尔可夫链和循环神经网络等序列模型因其捕捉隐含移动模式的能力而被广泛应用
- 然而,若未考虑地理信息及邻近轨迹间的关联性,这些序列模型在大范围区域的应用效果并不理想。
- 一些研究采用轨迹点的网格表示作为 GAN 模型的输入,但由于精度受限于网格大小,限制了生成轨迹的准确性。
- 以往研究中,如马尔可夫链和循环神经网络等序列模型因其捕捉隐含移动模式的能力而被广泛应用
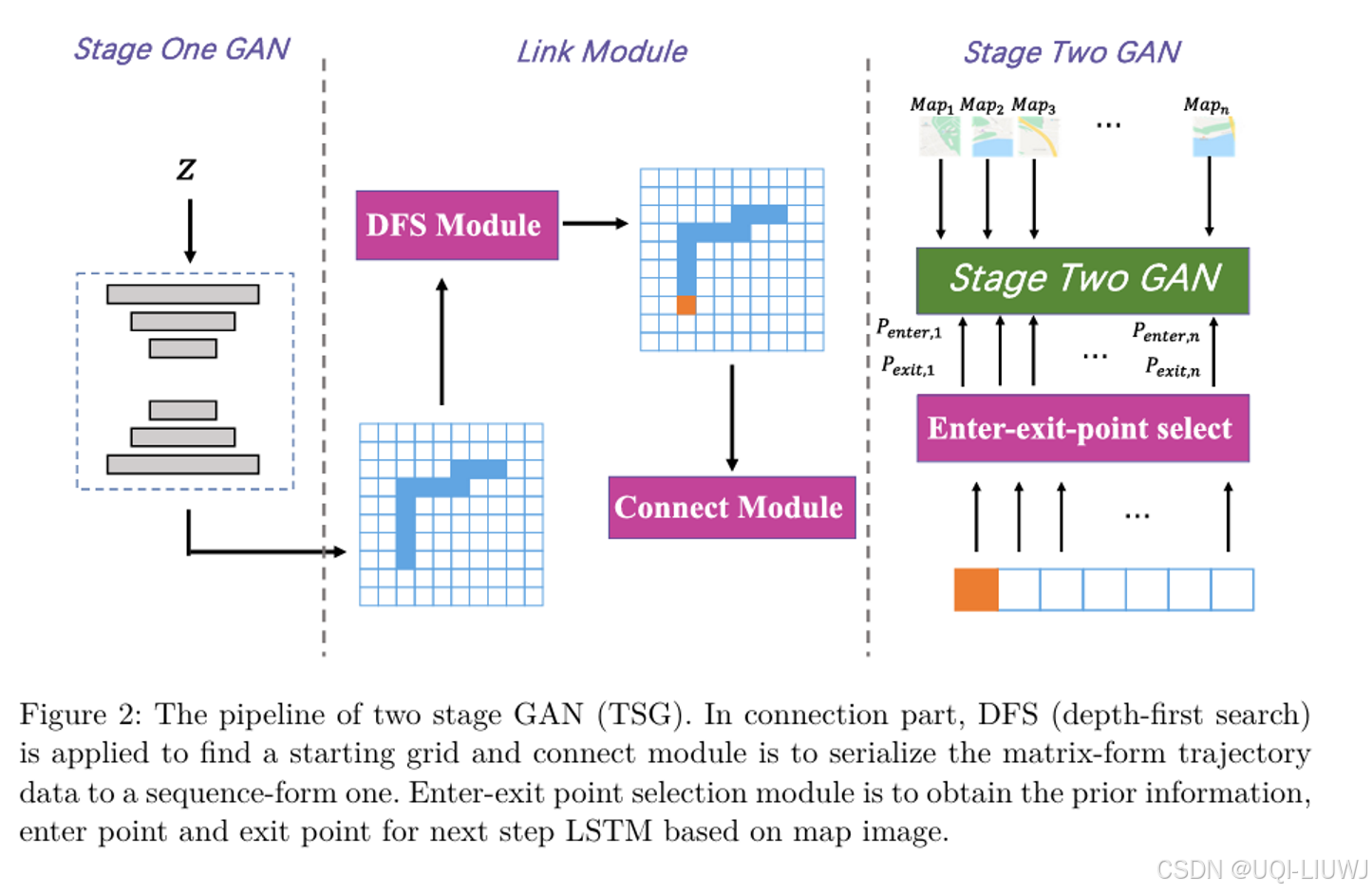
- 论文提出了一种两阶段的 GAN 方法,用于生成与原始数据集分布相似且符合道路网络的车辆轨迹
- 首先,将轨迹数据离散为网格形式,通过生成对抗网络模型生成网格形式的合成轨迹。
- 然后,为了在每个网格内具体化轨迹,将地图信息以图像形式作为条件输入,引入第二阶段的 GAN。
- 使用全卷积神经网络对地图图像进行编码(encoder),并使用两个并行的 LSTM 网络作为解码器(decoder)或生成器
- 判别器(discriminator)也以编码器的输出作为条件输入。
2 方法
2.1 符号说明
为原始轨迹数据
表示第 i 个 GPS 采样点的坐标
及其时间戳ti
- 在第一阶段的 GAN 中,我们将区域离散化为
的网格,每个轨迹点根据其位置落入某个网格
- 为记录轨迹信息,我们构建一个轨迹矩阵
- 矩阵中的元素
表示轨迹在第 (i,j) 个网格中停留的时间,
- 为记录轨迹信息,我们构建一个轨迹矩阵
- 当合成的轨迹数据采用网格表示后,第二阶段的 GAN 会将矩阵
转换为原始 GPS 点的序列,长度为 n,记为
2.2 第一阶段 GAN:基于网格的表示
- 同时训练两个模型:
- 一个生成模型 G,用于捕捉数据分布
- 一个判别模型D,用于判断样本是否来自训练数据而非 G
- 在第一阶段中,输入为网格表示形式的轨迹矩阵
- 训练目标是最小化训练轨迹数据分布 Pr 与生成数据分布 Pg 的联合分布之间的距离。
- WGAN-GP采用 Wasserstein 距离来设定优化目标,并引入梯度惩罚项以避免梯度消失或爆炸。
- 其损失函数为:
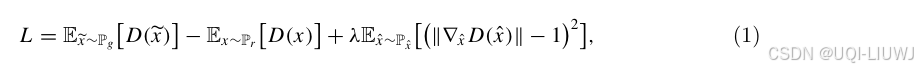
-
是在真实分布
与生成分布
之间的直线中均匀采样的点;
- D表示判别器
2.3 第二阶段:网格内的基于地图条件的 GAN
- 本部分旨在生成轨迹点在网格内的精确坐标。
- 给定某对起点
和终点
,需要生成一个轨迹点序列
,使其在对应地图图像中看起来真实可信。
- 相应的地图需要被编码为一个潜在向量,作为第二阶段 GAN 的条件输入
- 给定某对起点
- 我们注意到轨迹生成与图像描述在任务目标上有些相似,但也存在三点不同:
该问题是在连续空间中进行回归预测,而非离散的分类问题;
与图像描述从
<start>token 开始逐词生成不同,轨迹生成需要从一开始就考虑起点和终点,确保前几个点不偏离方向;轨迹生成和图像描述都从图像中提取信息,但前者更注重空间信息,后者更多使用语义信息。
判别器的作用是判断生成轨迹是否合理地位于道路网络中,从而对生成器进行约束
2.3.1 编码器
- 从原始地图图像中提取潜在特征,作为生成器的条件输入
- 与图像描述任务不同,这里采用了一个简单的全卷积架构FCN,因为道路图像更类似于语义分割任务
- 编码器接收原始地图图像
作为输入,得到道路特征图
2.3.2 生成器/解码器:对称 LSTM
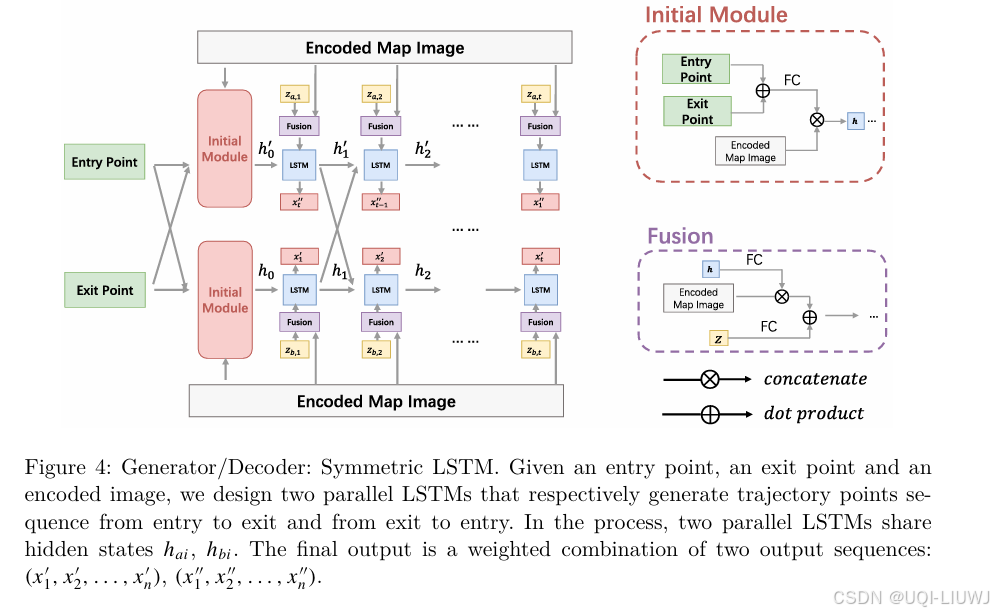
2.3.2.1 图像作为条件
- 所有轨迹点的坐标 (x, y) 在输入前都已归一化到 (-1, 1)范围内
- 借鉴神经图像描述的方式将地图图像作为条件信息,即将经过 FCN 编码的图像特征作为 LSTM 初始隐藏状态

是编码器提取的特征图
- E是位置嵌入层
,
是两层全连接网络
,
表示起点和终点
表示张量拼接
2.3.2.2 对称 LSTM
- 作者尝试过 vanilla LSTM,但发现其存在“暴露偏差”(exposure bias)问题(
- 即从起点开始递归生成会导致尾部轨迹偏离真实终点
- 论文观察到本问题具有对称性:从头到尾生成轨迹和从尾到头生成是等价的
- 受 Social-LSTM和 Bi-directional LSTM启发,提出一个由两个 LSTM 组成的解码器
- 分别从正序和逆序两个方向生成轨迹
- 在训练阶段,这两个 LSTM 分别按正序和逆序处理轨迹序列,采用“Teacher Forcing”策略,同时共享隐藏状态信息,以便选择正确方向
- 生成器损失函数结合了传统的对抗损失和
预测损失
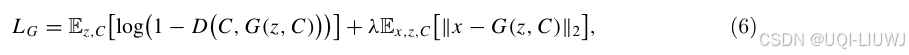
- x表示真实轨迹
- C表示地图特征作为条件输入
- 第一项是来自判别器的损失
- G(z, C)是生成器以潜变量 z 和条件 C$为输入生成的轨迹
2.3.3 基于 CNN 的判别器
- 我们在轨迹序列生成子任务中使用了基于 CNN 的判别器
- 给定一张地图图像和对应的轨迹点序列,判别器的任务是判断该点序列是否合理,即它应符合道路网络,且遵循真实轨迹所具有的模式。
- 地图图像已被编码为
,目标网格被划分为
的子网格
- 然后轨迹点序列也被转换为
的轨迹矩阵
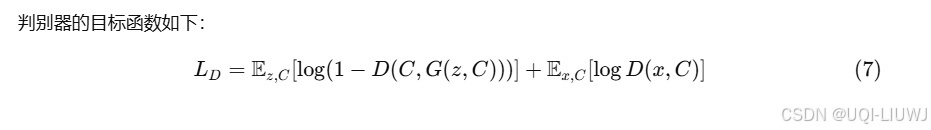
2.4 连接模块
- 在第一阶段中,GAN 生成多个轨迹矩阵,每一个代表一条合成轨迹
- 对于每一个生成的轨迹矩阵
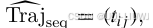 ,中 tij 表示在对应网格内的停留时间
,中 tij 表示在对应网格内的停留时间 - 应用连接算法(Connection Algorithm 1)将其转化为
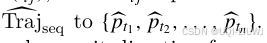
- 对于每一个生成的轨迹矩阵
- 根据网格序列,我们可以为每个网格确定一个入口方向和出口方向
- 基于道路网络,出口点可以从道路出口方向的边界中随机选择,而入口点则可由前一个网格的出口点推断
- 对于初始网格,我们从道路边界中随机选择一个入口点。
在获得了入口点、出口点和停留时间后,模型的第二部分便可继续执行任务,生成网格内的 GPS 点序列。
2.4.1 连接算法



也就是说,这个 Traj_mat 中的 非零网格 并不是全部都要用上的。
3 实验
3.1 数据集
- porto出租车数据集
- 整整一年内(2013 年 7 月 1 日至 2014 年 6 月 30 日),总计约 157 万条轨迹。
- 数据集中包含了 GPS 点序列,两个点之间的时间间隔为 15 秒。
- 考虑到行驶中的出租车 15 秒可能已移动很远的距离,为了获取更详细的道路信息并缩短时间间隔,在预处理阶段采用了三次插值方法,将点间间隔压缩到 3 秒,使数据更加稠密。
- 编码器所需的地图图像,我们使用地图 API 进行截图,裁剪并调整所有图像,使其与目标区域划分的网格区域相匹配
3.2 生成轨迹分布
3.2.1 整体分布
- 为评估生成轨迹分布与真实轨迹分布之间的统计相似性,选用了 Jensen-Shannon 散度(JSD)作为评价指标
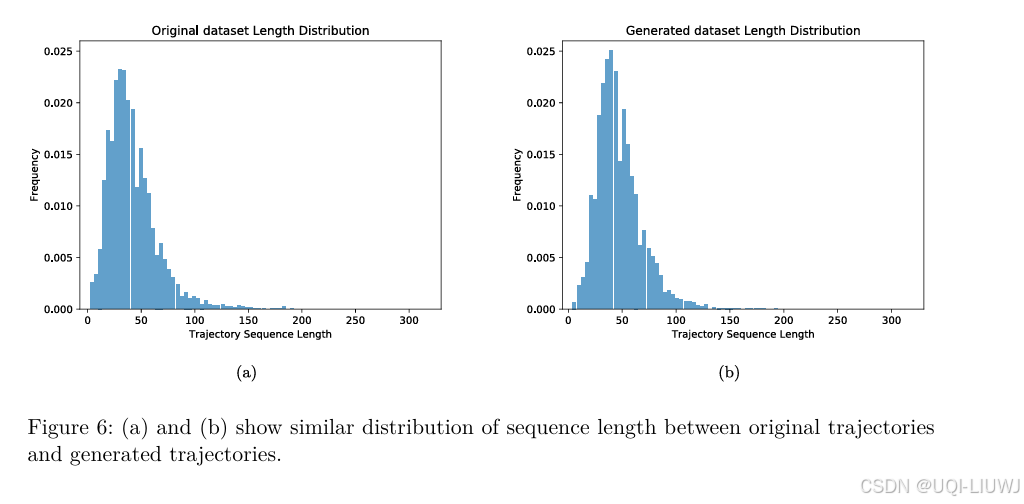
3.2.2 轨迹长度分布
- 从两个角度评估轨迹的“长度”分布:序列长度和距离长度
- ps(l) 表示轨迹序列长度为 l 的概率。
- 由于点与点之间的时间间隔是固定的,ps(l)实际上反映了行驶时间的分布。
- pd(l)表示轨迹实际距离为 lll 的概率。
- 轨迹距离通过公式
计算,其中 dis(pi,pi+1)表示两个点之间的地理距离。
- 轨迹距离通过公式
- ps(l) 表示轨迹序列长度为 l 的概率。
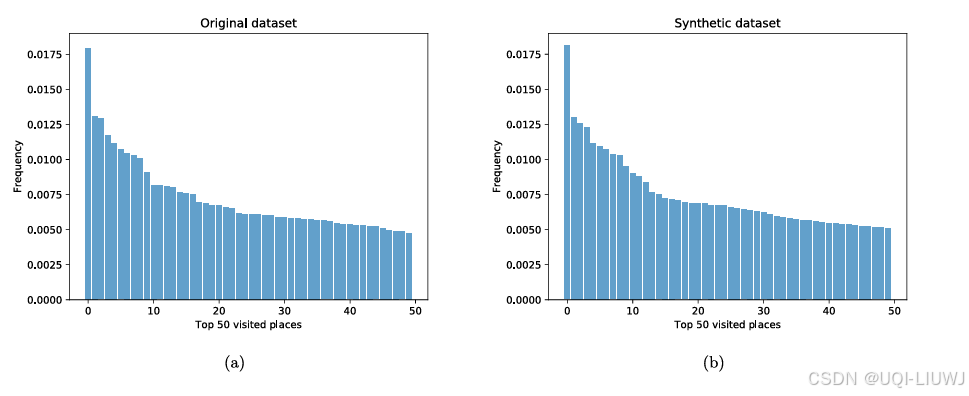
3.2.3 访问次数最多的前 N 个地点(Top N Visited Places)
一个地点定义为可在第一阶段网格中近似表示的小区域
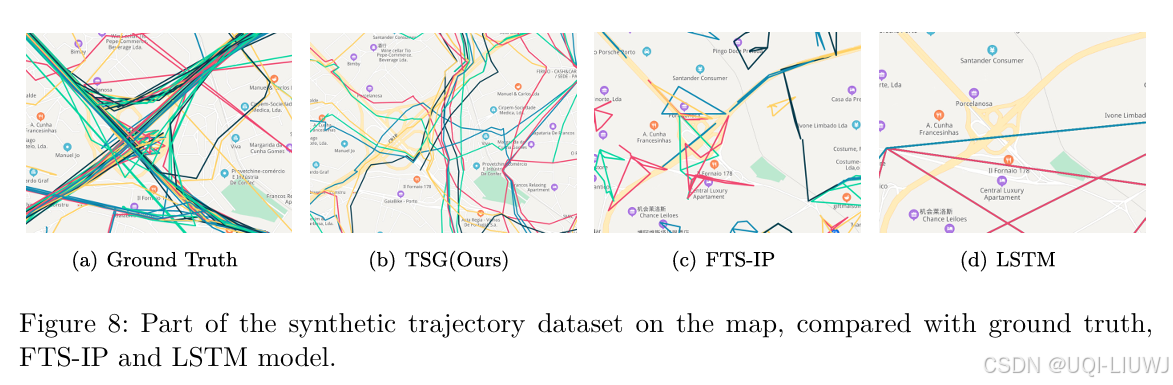
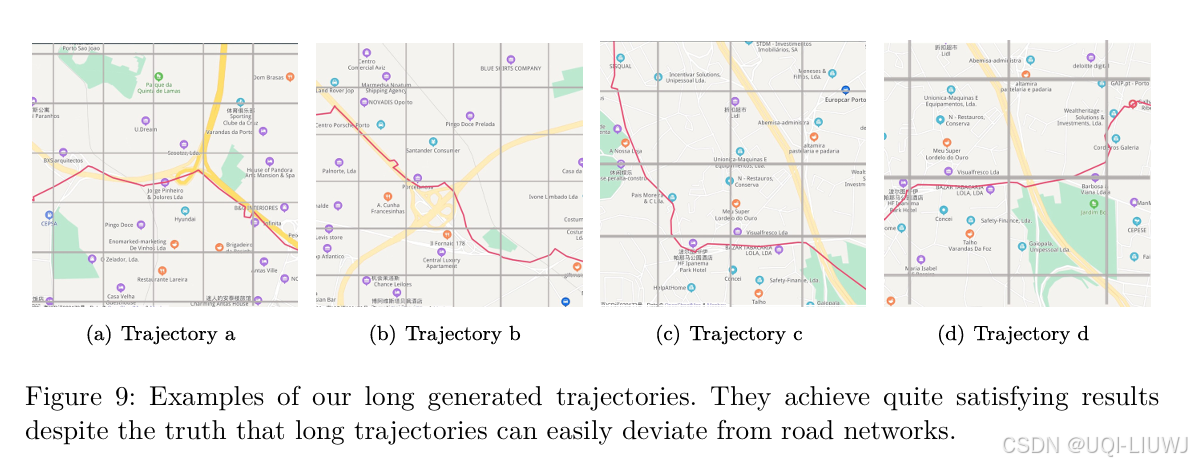
3.3 道路网络匹配准确率
- 将生成的轨迹绘制在地图上,与其他模型进行对比,以判断其真实性
4 总结
最终轨迹生成的时候,流程是这样的
- 第一阶段:输入一个随机向量,输出一个轨迹矩阵
Traj_mat(每个网格的停留时间) - 中间步骤:连接模块 Link Module
从
Traj_mat中找出一个连接路径(即网格序列)Grid_seq,并确定其起点、终点
第二阶段:输入地图图像、起点坐标、终点坐标,输出一条连续的 GPS 点轨迹
Traj_seq = [(x₁, y₁), (x₂, y₂), ..., (x_T, y_T)]