一、结构
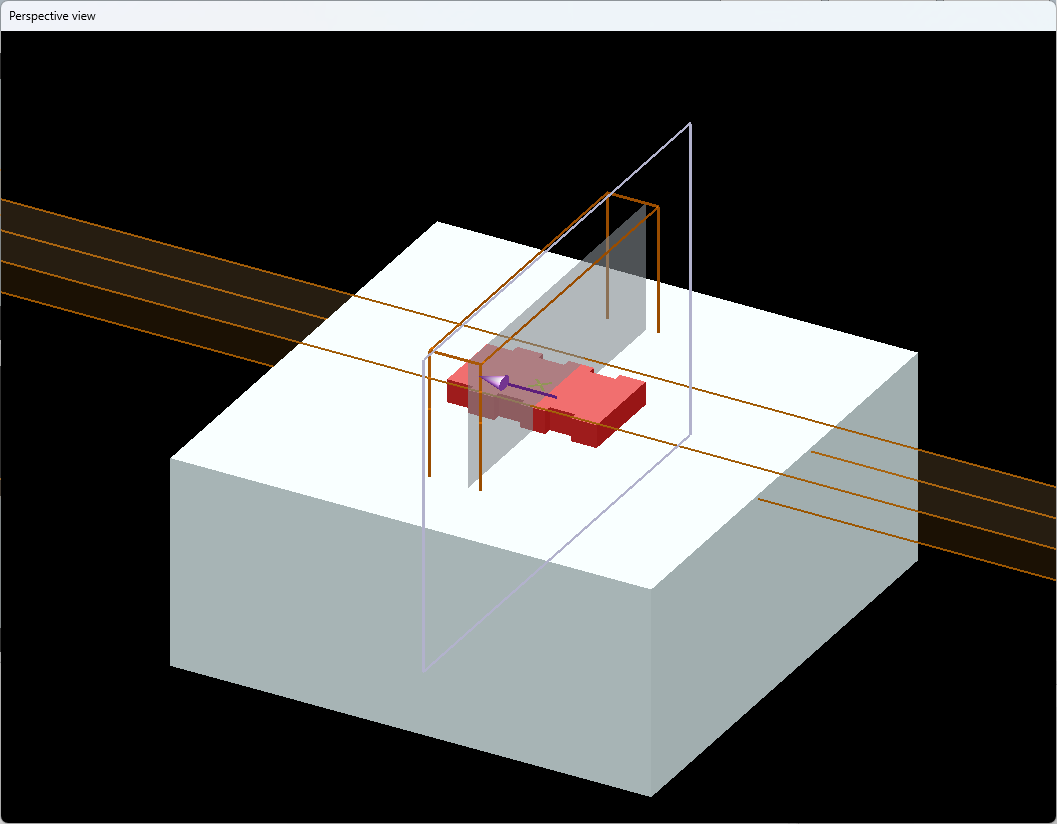
波导布拉格光栅本质上是一种"光学波长筛子"——通过在直波导(如光纤或集成光路)内部制造纳米级周期性折射率调制(相当于每隔固定距离刻一道"光学刻痕"),使得当光传播时,只有满足布拉格条件(λ=2nΛ)的特定波长会因相干叠加被强烈反射,就像面对一面智能镜子,而其他波长则直接透射。这种周期性结构形成了一维光子带隙(即针对特定波长范围的光禁止传播),其原理类似于晶体对X射线的布拉格衍射,但限制在一维空间实现。作为介电镜(不依赖金属反射的光学反射镜),它能以极高效率(>99%)和窄带宽(可小于0.1nm)实现波长选择,因此成为波分复用系统中的关键滤光片、激光器的波长锁定元件以及高精度传感器的核心部件,其性能由光栅周期Λ、折射率调制深度Δn和作用长度L共同决定。
主要用作"光学筛子",例如:
- 在光纤通信中分离不同颜色的信号
- 在激光器中锁定特定波长
- 在传感中检测波长变化(如温度/应力测量)
构建二氧化硅衬底
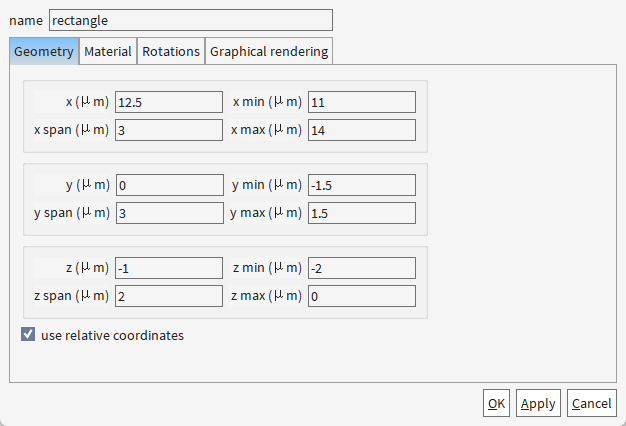
为什么要选择二氧化硅呢?
(1)光学波导衬底
低光学损耗:在通信波段(如1550nm)损耗极低(<0.1dB/cm),避免干扰光栅性能仿真
折射率匹配:n≈1.44(@1550nm),与硅(n≈3.48)形成强光场约束,适合构建高对比度波导结构
(2)热力学稳定平台
热膨胀系数低(0.5×10⁻⁶/°C):保证光栅在温度变化时周期Λ稳定性
熔点高(~1700°C):兼容高温工艺(如硅光栅的退火处理)
(3)化学钝化层
保护光栅结构免受环境腐蚀(尤其对氢敏的光纤光栅)
注:通常取≥2μm以满足光场衰减至<1%(防止衬底泄漏模),本例选择的是2um
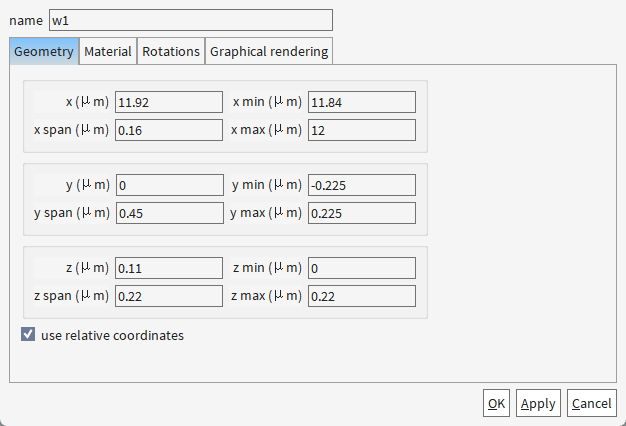
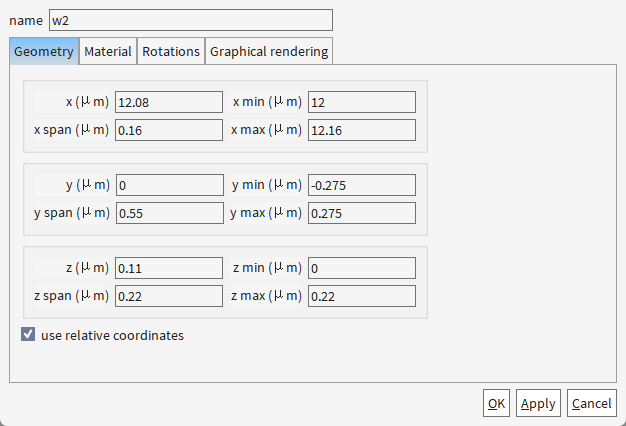
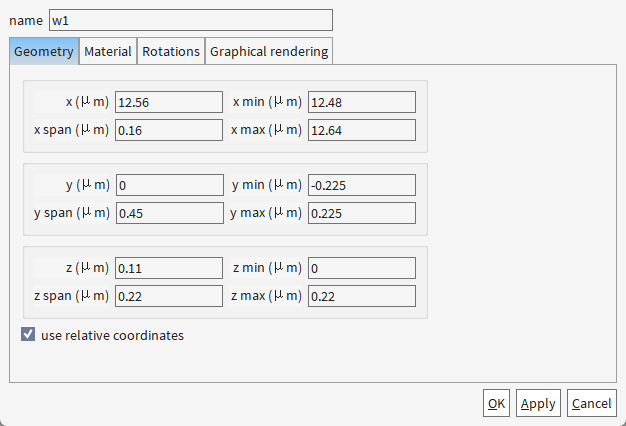
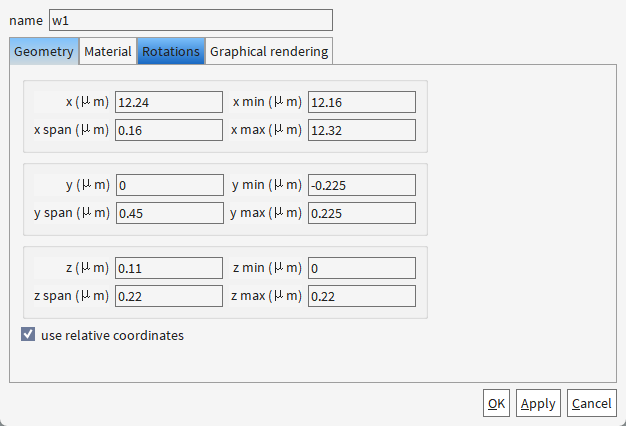
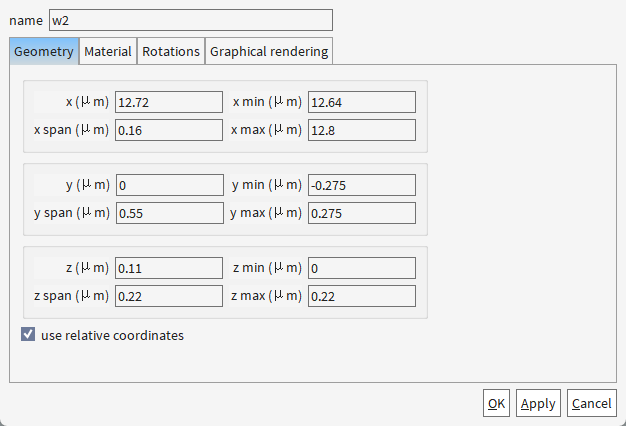
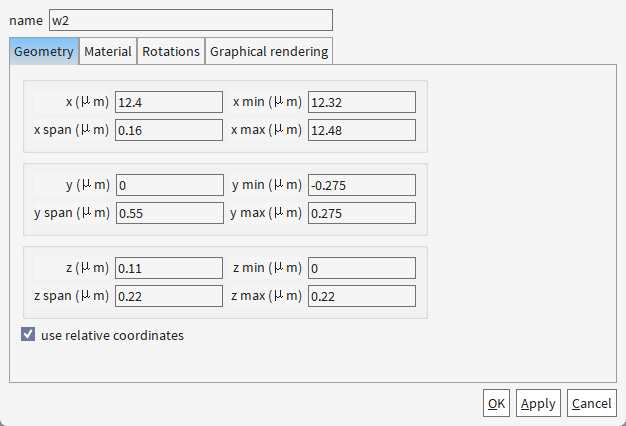
材料设置均为
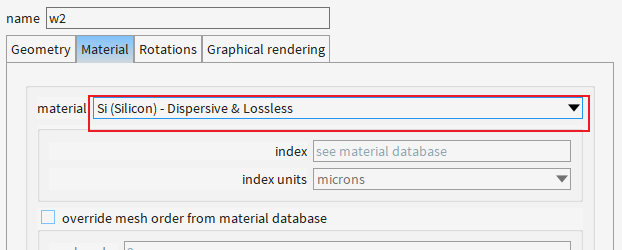
首先强调一下波导折射率差的重要性:
布拉格光栅的反射本质是分布式反馈:
- 每个折射率突变点(Δn界面)都会产生微弱反射(约10⁻⁶量级)
- 当所有反射光满足 相干叠加条件 时,特定波长(λ_B)被强烈反射
- 折射率差Δn决定了反射强度
那为什么本例材料都是一样的?还怎么实现波长选择性反射?
本例中折射率差是通过几何结构隐式实现
实际物理器件:布拉格光栅通过周期性改变材料折射率(如紫外曝光使光纤纤芯Δn≈10⁻⁴~10⁻³)实现反射。
仿真简化:在FDTD中,可通过周期性改变波导宽度(如图中阶梯状结构)等效实现折射率调制:
宽部:有效折射率n_eff较高(更多光场约束在硅中)
窄部:n_eff较低(更多光场进入SiO₂包层)
效果:形成等效的折射率周期Δn_eff,满足布拉格条件 λ=2(n_eff)Λ
为啥选择这个材料呢?
1. 色散效应(Dispersive)的精确建模
普通硅模型:通常假设折射率为固定值(如n≈3.48@1550nm),忽略其随波长变化的特性。
Dispersive模型:通过 Sellmeier方程 或 Lorentz模型 描述折射率的波长依赖性,例如:
在1.15–1.8μm波段,硅的折射率会随波长变化(如1550nm→3.48,1310nm→3.51)。
这对于仿真布拉格光栅、微环谐振器等波长敏感器件至关重要,避免因忽略色散导致谐振峰偏移或带宽计算错误。
2. 无损耗(Lossless)假设的适用场景
普通硅模型:可能包含默认的吸收损耗(如载流子吸收或双光子吸收效应)。
Lossless模型:假设材料无吸收(消光系数k=0),适用于:
低功率仿真:当光功率不足以激发非线性效应(如双光子吸收)时,简化计算。
无源器件分析:如波导传输、耦合器等,无需考虑热效应或光损伤。
注意:若需模拟高功率场景(如硅光调制器),需切换至含损耗模型(如"Si (Silicon) - Dispersive & Lossy")。
二、添加FDTD
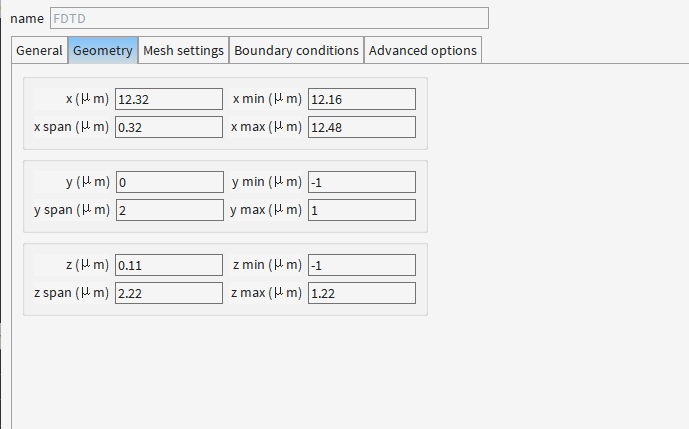
y span为啥这么大?
波导模式完整捕获
- 典型硅波导(如220 nm×450 nm)的模场直径约1–1.5 μm,2 μm跨度确保:
- 场衰减至背景噪声水平(避免截断效应)
- 留足PML吸收层空间(图中y方向用8层PML)
- 典型硅波导(如220 nm×450 nm)的模场直径约1–1.5 μm,2 μm跨度确保:
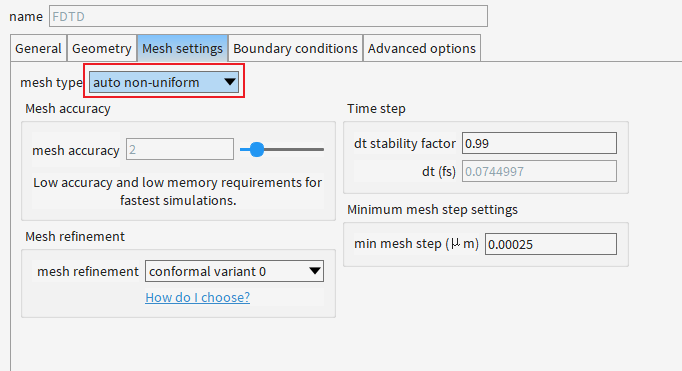
| 选项 | 工作原理 | 优点 | 缺点 |
|---|---|---|---|
| Auto Non-Uniform | 软件自动识别结构特征(如边缘、界面),在关键区域加密网格,均匀区域保持稀疏 | 智能平衡精度与速度 | 局部加密策略不可控 |
| Custom Non-Uniform | 用户手动定义加密区域和步长(如指定某坐标范围网格步长5nm) | 精准控制关键区域分辨率 | 配置复杂,计算量大 |
| Uniform | 整个仿真区域采用固定网格步长(如全局0.1μm) | 结果绝对可重复,设置简单 | 内存消耗大,效率低 |
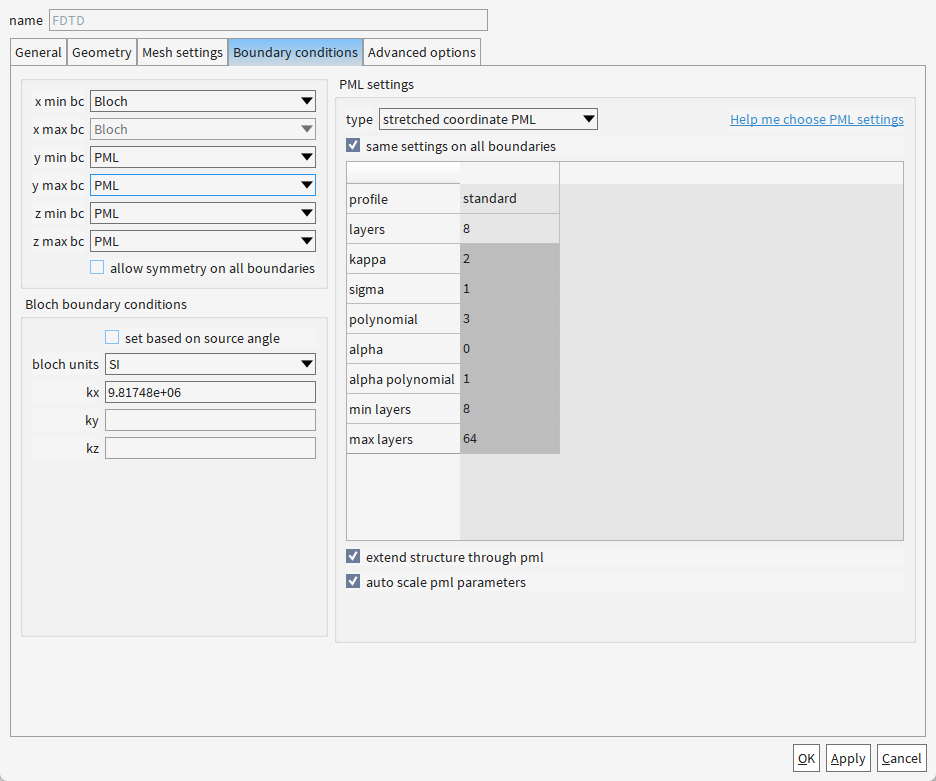
为啥用Bloch边界条件?
- 周期性匹配:精确模拟无限周期性结构(如光栅的重复单元),避免PML对周期性的破坏
- 波矢控制:通过设置
kx, ky, kz定义布洛赫波矢(对应光子能带计算中的k点) - 计算效率:仅需仿真单个周期单元,大幅减少计算量
可以看到y方向是用了8层PML
| 层号 | σ/κ值 | 作用机制 | 类比 |
|---|---|---|---|
| 第1层 | 最小 | 缓慢开始吸收,避免阻抗突变 | 吸音棉表面最柔软 |
| ... | 渐变增大 | 逐步增强吸收 | 吸音棉密度向内增加 |
| 第8层 | 最大 | 完全衰减残余场,终止传播 | 最内层高密度隔音材料 |
| 层数 | 吸收效果 | 计算量 | 适用场景 |
|---|---|---|---|
| 4层 | 基本吸收(-30dB) | 最小 | 快速预览,低精度需求 |
| 8层 | 高吸收(-60dB) | 适中 | 常规硅光子器件(本例选择) |
| 16层 | 极致吸收(-90dB) | 最大 | 超低反射需求(如激光腔仿真) |
1. x方向波矢(kx=9.81748e+06 m⁻¹) 的物理意义
本质:波矢 k 表示光波在周期性结构中的相位变化速率,单位为 m⁻¹(每米的弧度)。
kx = 2π / Λ # Λ为结构周期(图中Λ≈640nm)
= 2π / (640e-9)
≈ 9.81748e+06 m⁻¹
告诉仿真软件:光波每前进一个周期(Λ),其相位增加 2π(即波形完全重复)。
2. 为什么单位选 SI?
选项 |
单位制 |
适用场景 |
图中选择原因 |
|---|---|---|---|
|
国际单位(m⁻¹) |
直接关联实际尺寸(如Λ=640nm→k=9.81e6 m⁻¹) |
用户需输入实际波矢值,便于物理对照 |
|
归一化单位(2π/Λ) |
能带计算时简化k范围(0~1对应0~π/Λ) |
未选,因当前为单点k值分析,非能带扫描 |
3. bandstructure 选项的作用
若勾选:
kx/ky/kz的取值范围自动归一化为 0到1(对应实际k值为0到π/Λ)。
专门用于能带计算(扫描k值绘制ω-k曲线)。
图中未勾选:
说明当前是单点k值分析(如固定入射角下的反射谱),而非全波段能带计算。
4. ky 和 kz 为何留空?
y/z方向非周期性:
若结构仅在x方向周期性重复(如布拉格光栅),y/z方向需用PML吸收边界,无需布洛赫条件。特殊需求:
若结构在y/z方向也有周期性(如三维光子晶体),则需填写对应k值。
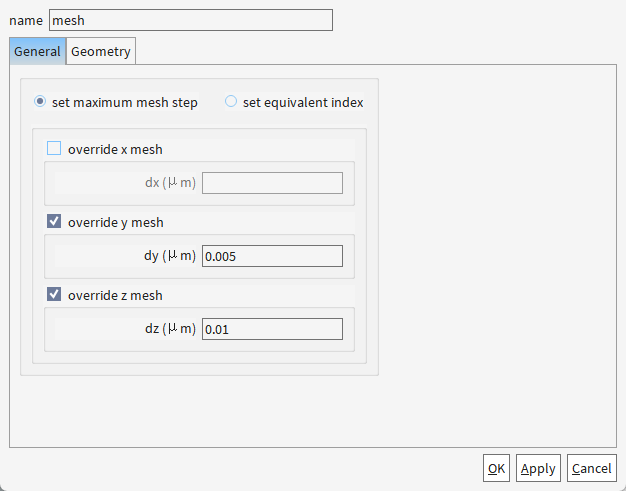
(1) z方向10nm的合理性
220nm硅层:10nm网格相当于将高度分为22份,足以解析:
基模场分布(峰值区)
顶部/底部SiO₂界面的倏逝场(衰减长度~100nm)
(2) y方向5nm的高精度
450nm波导宽度:5nm网格(宽度方向90份)可精确模拟:
侧壁倾角效应(如85°刻蚀角)
边缘散射损耗(对偏振敏感)
(3) x方向不覆盖
依赖
auto non-uniform自动优化,优先加密:光栅周期边缘(如果存在)
模式转换区(如锥形耦合器)
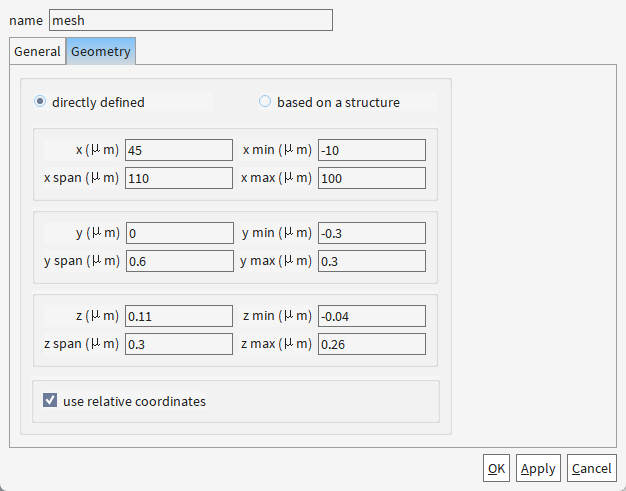
当前大跨度x方向设置是为了:
- 精确模拟多周期光栅的集体反射效应
- 隔离边缘数值干扰,确保中心区域(光栅主体)的仿真准确性
- 兼容参数化扫描(通过相对坐标保持结构居中)
三、添加光源
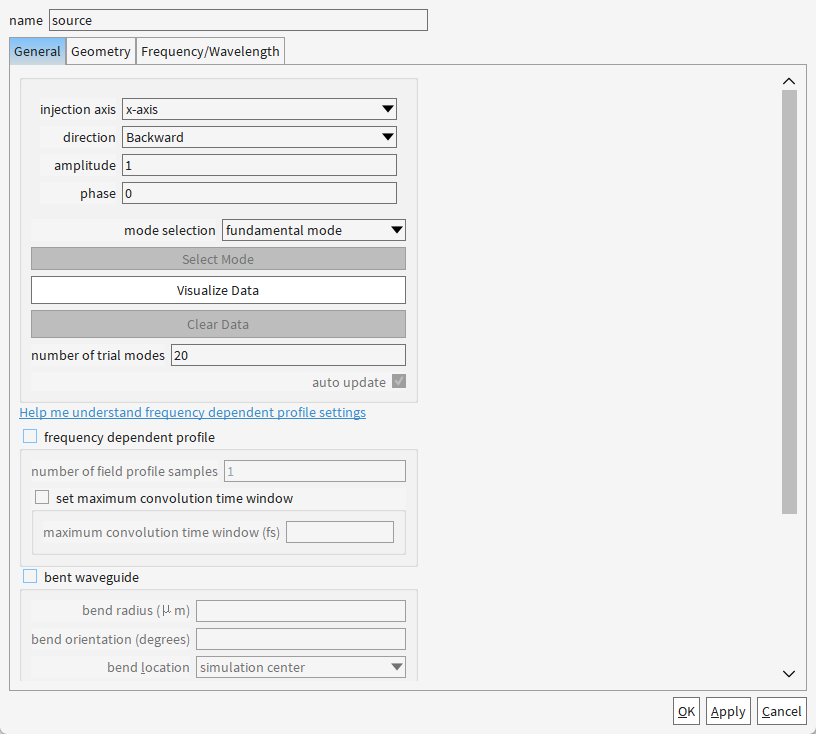
注:number of trial modes=20是搜索上限,实际模式数由波导物理特性决定。
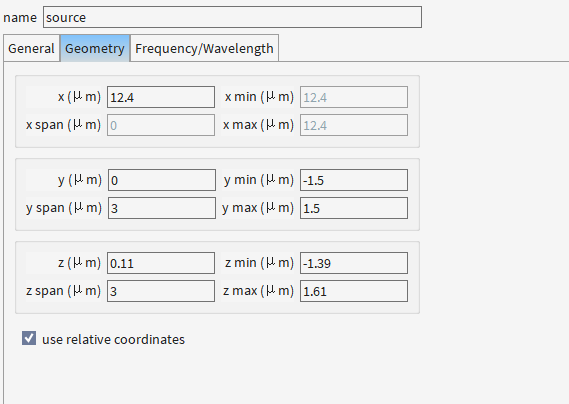
为啥光源被放置在左侧波导内部而非两波导中间?
(1) 物理真实性
现实中的耦合器:光总是从一个输入波导进入(如图中左侧波导),通过倏逝场耦合到相邻波导,而非凭空在两波导中间产生光。
仿真一致性:光源位置需还原真实实验场景(如光纤连接左侧波导入射)。
(2) 模式选择性
单波导激发:将光源放在一侧波导内,可精确控制激发的是左侧波导的基模(如TE₀模式)。
中间放置的问题:
若光源放在两波导中间,会同时激发两个波导的混合模式(非物理状态);
导致耦合效率计算失真(无法区分输入和耦合功率)。
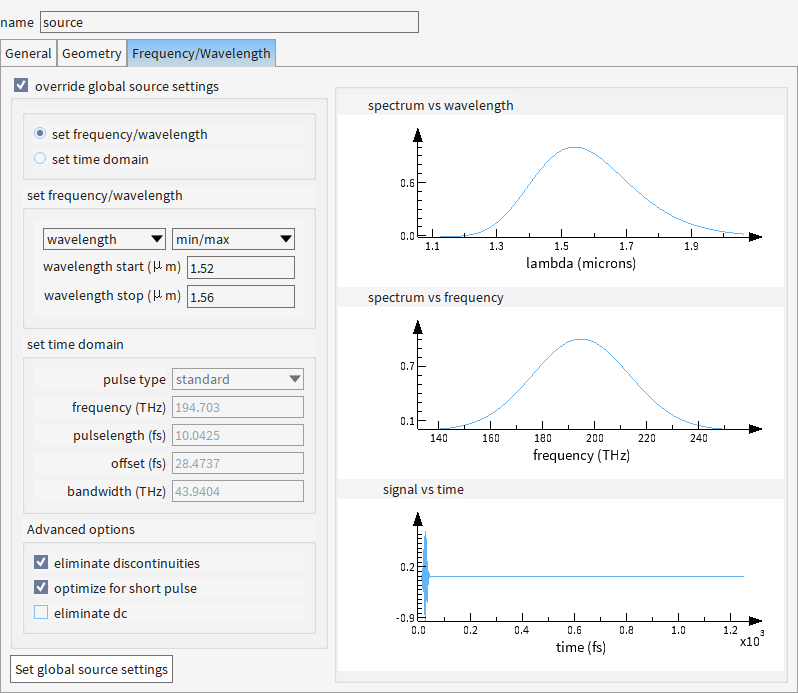
光源会发射 1520nm至1560nm范围内的光(覆盖C波段通信波长)
四、添加分析组
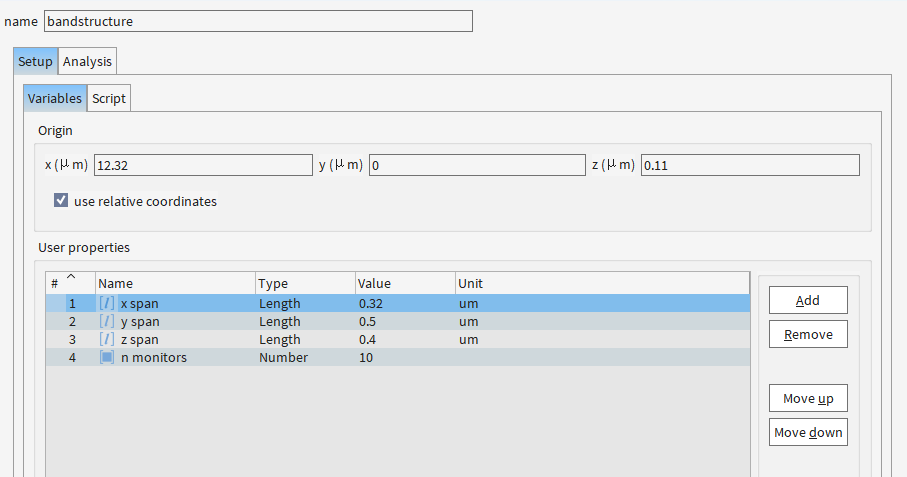
以下代码作用是创建多个随机分布的时间监视器(time monitors),目的是分析光子晶体或周期性结构的能带特性(bandstructure)
deleteall;
##############################################
# Bandstructure
# This script creates n randomly positioned monitors
#
# Input properties
# x,y,z span: The span of the random cloud of monitors
# n monitors: The number of monitors
#
# Tags: bandstructure time monitors band gap photonic crystal resonant frequencies
#
# Copyright 2012 Lumerical Solutions Inc
##############################################
# simplify variable names by removing spaces
x_span = %x span%;
y_span = %y span%;
z_span = %z span%;
n_monitors = %n monitors%;
# Set the random number generator seed. Change this values
# to get different random orientation of objects
randreset(123); # 固定种子为123,确保每次运行脚本生成的随机位置一致(结果可重复)。
for(i=1:n_monitors) {
addtime;
set("name","m"+num2str(i));
set("x",(rand-0.5)*x_span); # x位置:[-0.5x_span, 0.5x_span]
set("y",(rand-0.5)*y_span); # y位置:[-0.5y_span, 0.5y_span]
set("z",(rand-0.5)*z_span); # z位置:[-0.5z_span, 0.5z_span]
}
| 代码变量 | 图中参数位置 | 值(示例) | 物理意义 |
|---|---|---|---|
x_span = %x span% |
User properties → x span |
0.32 μm | 监视器随机分布的x方向范围 |
y_span = %y span% |
User properties → y span |
0.5 μm | y方向范围(通常为波导宽度方向) |
z_span = %z span% |
User properties → z span |
0.4 μm | z方向范围(通常为波导高度方向) |
n_monitors = %n monitors% |
User properties → n monitors |
10 | 监视器数量(越多统计越准,但计算量越大) |
set("x",(rand-0.5)*x_span); 这句代码解释:
rand是Lumerical内置函数,会生成一个 0到1之间的随机数(比如0.2、0.7等)。- 减去0.5 是为了把范围从 [0,1] 转换成 [-0.5, 0.5]:
- 原来:0 → 1
- 现在:-0.5 → +0.5
- 直接
rand:监测器只会出现在 正半轴(0到x_span),不符合对称需求。 -
rand-0.5:让监测器能均匀分布在 中心两侧(-x_span/2到+x_span/2)。
需要注意的是
勾选这个
勾选此选项后,该分析组(bandstructure)将被标记为“构造组”,意味着它仅在仿真前执行一次(通常用于创建几何结构或初始化设置),而不会在每次参数扫描或优化时重复运行。
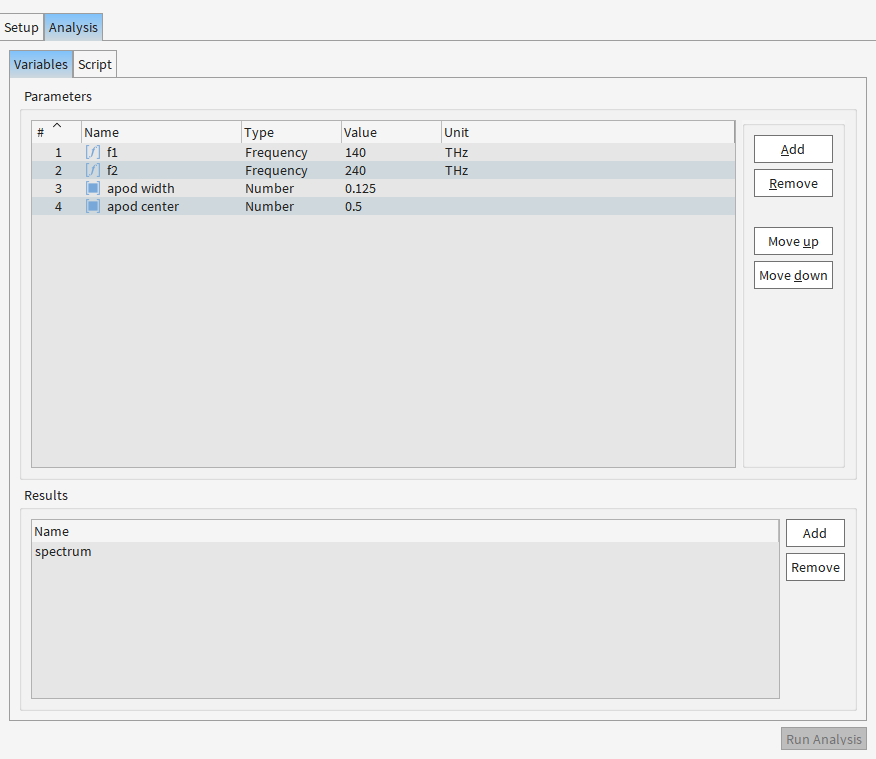
##########################################################################
# Bandstructure
# This script is to be used in bandstructure calculations.
#
# Input properties
# f1, f2: min, max frequency of interest
# apod width: apodization width as a fraction of total simulation time
# apod center: center location of the apodization filter as a fraction of
# total simulation time
#
# Output properties
# spectrum: result from the summation of ffts of time signals from each
# monitor - this is a spectrum with peaks at resonant frequencies
#
# Tags: bandstructure time monitors band gap photonic crystal resonant frequencies
#
# Copyright 2012 Lumerical Solutions Inc
###########################################################################
# simplify variable names by removing spaces
apod_width = %apod width%; # 读取"apod width=0.125"(高斯窗宽度)
apod_center = %apod center%; # 读取"apod center=0.5"(窗函数中心位置)
n_monitors = %n monitors%;
if (f1<=0) { f1 = f2/10000; } # don't allow f1=0, as this causes a minor problem: f=0 corresponds to lambda=infinity, and the infinity causes problems in the data visualizer.
t = getdata("m1","t"); # 从第一个监视器(m1)读取时间轴数据
fs = 0; # 初始化频谱累加器
# 逐个读取每个监视器记录的电场随时间变化的数据
for(j=1:n_monitors) { # 遍历所有监视器(m1到m10)
for (component_i=1:3) { # loop over field components # 循环3个电场分量(Ex, Ey, Ez)
if (component_i==1) { component="Ex"; }
if (component_i==2) { component="Ey"; }
if (component_i==3) { component="Ez"; }
signal = pinch(getdata("m"+num2str(j),component)); # 获取该分量的时域信号
# 加窗函数,消除仿真开始/结束时的突变噪声,让频谱分析更准确
signal = signal*exp( - 0.5*(t-max(t)*apod_center)^2/(apod_width*max(t))^2);
# 将时域信号转换为频域,abs()^2表示计算功率谱
f = linspace(f1,f2,5000); # 生成140-240THz的5000个频率点
fs = fs + abs(czt(signal,t,2*pi*f))^2; # 对信号做FFT并累加到总频谱
}
}
# create data set
spectrum = matrixdataset("spectrum");
spectrum.addparameter("f",f,"lambda",c/f); # 添加频率和波长列
spectrum.addattribute("fs",fs); # 添加频谱强度数据
| 代码部分 | 图中参数 | 用户设置值 | 作用 |
|---|---|---|---|
apod_width |
apod width | 0.125 | 控制高斯窗的宽度(越小越聚焦中间数据) |
apod_center |
apod center | 0.5 | 窗函数中心位置(0.5=正中间) |
f1, f2 |
f1, f2 | 140THz, 240THz | 分析的频率范围 |
(1)signal = pinch(getdata("m"+num2str(j),component));
pinch()的具体功能
- 输入:多维数组(如从监视器读取的电场数据可能是3D数组:时间步×空间点×分量)
- 输出:移除所有长度为1的维度,返回紧凑格式的数组
- 例如:若原始数据形状为
(100,1,1)(100个时间点),pinch()后变为(100,)
- 例如:若原始数据形状为
确保signal变为纯一维数组,避免后续FFT计算因维度问题报错。
(2)最终输出一个表格,包含两列:
f:频率(140-240THz)fs:对应频率的光强度(峰值即光子晶体的允许通过频段)
(3)上述代码的工作流程:
1. 参数初始化阶段
从GUI界面读取输入参数(对应图中
Variables标签页):f1=140 THz,f2=240 THz→ 定义目标频率范围(约1250nm~714nm波长)apod_width=0.125,apod_center=0.5→ 设置高斯窗函数参数,用于抑制时域信号截断噪声n_monitors→ 监视器数量(图中未显示值,通常≥10)
2. 数据采集阶段
遍历所有时间监视器(
m1到mN):逐点读取三个电场分量(
Ex,Ey,Ez)的时域信号物理意义:记录光子晶体中不同空间位置的光场随时间演化
3. 信号预处理阶段
加窗处理(Apodization):
目的:通过高斯窗函数抑制仿真初始/终止阶段的非物理振荡(Gibbs现象)
参数控制:
窗宽
apod_width=0.125→ 控制衰减速度(值越小,窗口越窄)中心
apod_center=0.5→ 窗函数对称中心(50%仿真时长位置)
4. 频谱分析阶段
快速傅里叶变换(FFT):
使用线性调频Z变换(
czt)计算频域响应,优于传统FFT的分辨率频率采样点:
f = linspace(f1,f2,5000)→ 在140-240THz生成5000个均匀间隔点
功率谱累加:
优势:通过多监视器统计平均,提高信噪比
5. 结果输出阶段
生成结构化数据集:
输出格式:矩阵数据集,可直接用于绘制能带图或导出至其他工具
model分析组:
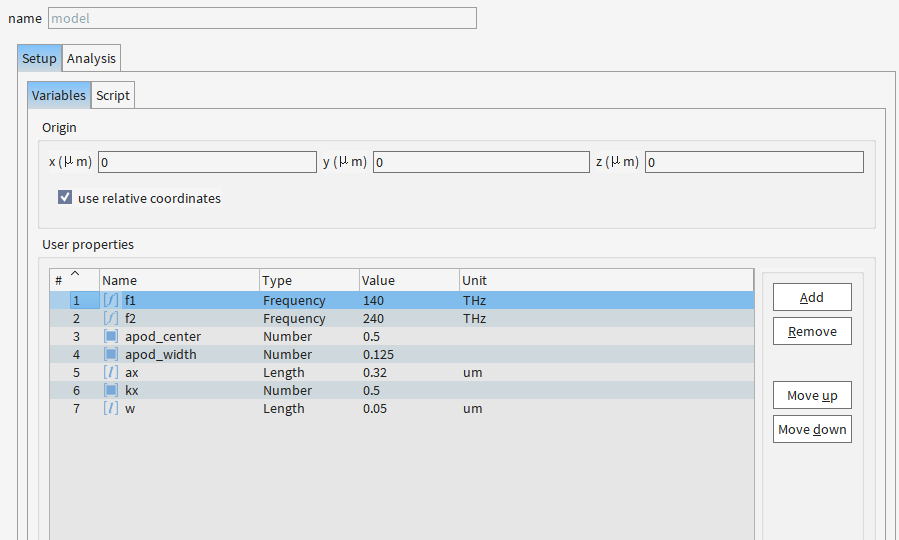
| 类型(Type) | 物理意义 | 典型应用场景 | 示例(图中Value) | 单位(Unit) |
|---|---|---|---|---|
| Frequency | 光的振荡频率 | 定义仿真分析的频率范围 | f1=140, f2=240 |
THz(太赫兹) |
| Number | 无量纲的纯数值 | 控制算法参数或归一化变量 | apod_center=0.5 |
(无) |
| Length | 几何尺寸的长度量 | 设置波导宽度、结构周期等物理尺寸 | ax=0.32, w=0.05 |
μm(微米) |
脚本是用于 配置周期性结构(如光子晶体或光栅)的仿真参数,主要分为 FDTD仿真区域设置 和 能带分析(bandstructure)参数设置 两部分
# set period and bloch vector of simulation
name="FDTD";
setnamed(name,"x span",ax); # 设置仿真区域x方向跨度(ax为用户定义的周期长度)
# 布洛赫波矢单位设为国际单位(m⁻¹)
setnamed(name,"bloch units","SI"); # we generally use bandstructure units, but for the simulation region, it's
# 计算x方向波矢kx(SI单位:kx*2π/ax)
setnamed(name,"kx",kx*2*pi/ax); # most convenient to use SI units becuase kx and ky can have different
# set period and apodization settings for banstructure analysis object
name="bandstructure";
setnamed(name,"x span",ax); # 能带分析区域与仿真区域周期一致
setnamed(name,"apod center",apod_center); # 设置加窗函数中心位置
setnamed(name,"apod width",apod_width); # 加窗宽度
setnamed(name,"f1",f1); # 最小分析频率
setnamed(name,"f2",f2); # 最大分析频率
select('w1');
set('y span',0.5e-6-w); # 设置波导w1的宽度为0.5μm - w
select('w2');
set('y span',0.5e-6+w); # 设置波导w2的宽度为0.5μm + w 
下列代码是用于 从能带分析结果中提取关键光学参数(如带宽、中心波长、耦合系数等)
spectrum = getresult('bandstructure','spectrum'); # 获取能带分析结果
fs = spectrum.fs; # 频谱强度
lambda = spectrum.lambda; # 波长数组(单位:m)
bandwidth = matrix(length(w)); # 初始化带宽数组
center_wavelength = matrix(length(w)); # 初始化中心波长数组
temp = fs(1:length(lambda)); # 提取当前频谱数据
ind = findpeaks(temp,2); # 找到前两个显著峰值的位置索引
bandwidth = abs(lambda(ind(2))-lambda(ind(1))); # 计算带宽(Δλ)
center_wavelength = lambda(ind(1)) + bandwidth/2; # 计算中心波长(λ₀)
ng = 4.3874; # 群折射率
kappa = pi*ng*bandwidth/(center_wavelength^2); # 计算耦合系数| 变量 | 物理意义 |
|---|---|
bandwidth |
光子带隙/谐振峰带宽 |
center_wavelength |
中心波长 |
kappa |
光栅耦合系数 |
五、添加参数扫描
定义了一个 波导宽度偏移量(w)的参数扫描任务。Ranges(范围扫描)生成5个均匀分布的w值,输出带宽(bandwidth)和耦合系数(kappa)随w的变化规律
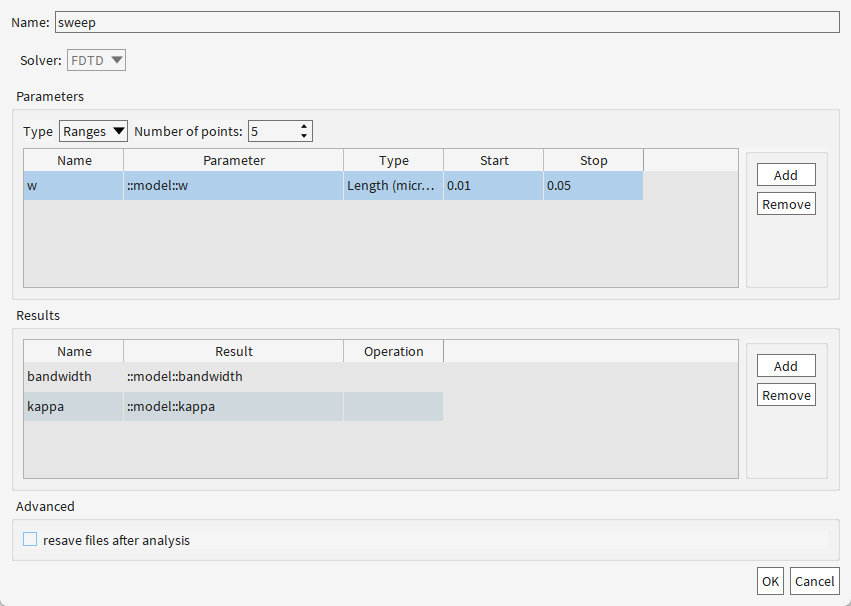
| 选项 | 含义 | 适用场景 | 示例 |
|---|---|---|---|
| Ranges | 范围扫描:在起始值(Start)和终止值(Stop)间生成均匀间隔的多个值 | 需要连续参数优化(如带宽随宽度变化曲线) | w=0.01, 0.02, 0.03, 0.04, 0.05 μm |
| Values | 离散值扫描:直接输入一组不连续的具体数值 | 测试特定参数组合(如工艺允许的固定尺寸) | w=0.01, 0.03, 0.05 μm(非均匀分布) |
| 参数 | 图中值 | 物理意义 |
|---|---|---|
| w (Start) | 0.01 μm |
波导宽度偏移量的最小值(基准宽度0.5μm → 实际宽度0.49μm) |
| w (Stop) | 0.05 μm |
波导宽度偏移量的最大值(实际宽度0.55μm) |
| Number of points | 5 |
扫描点数(点数越多曲线越平滑,但计算量越大) |
六、运行
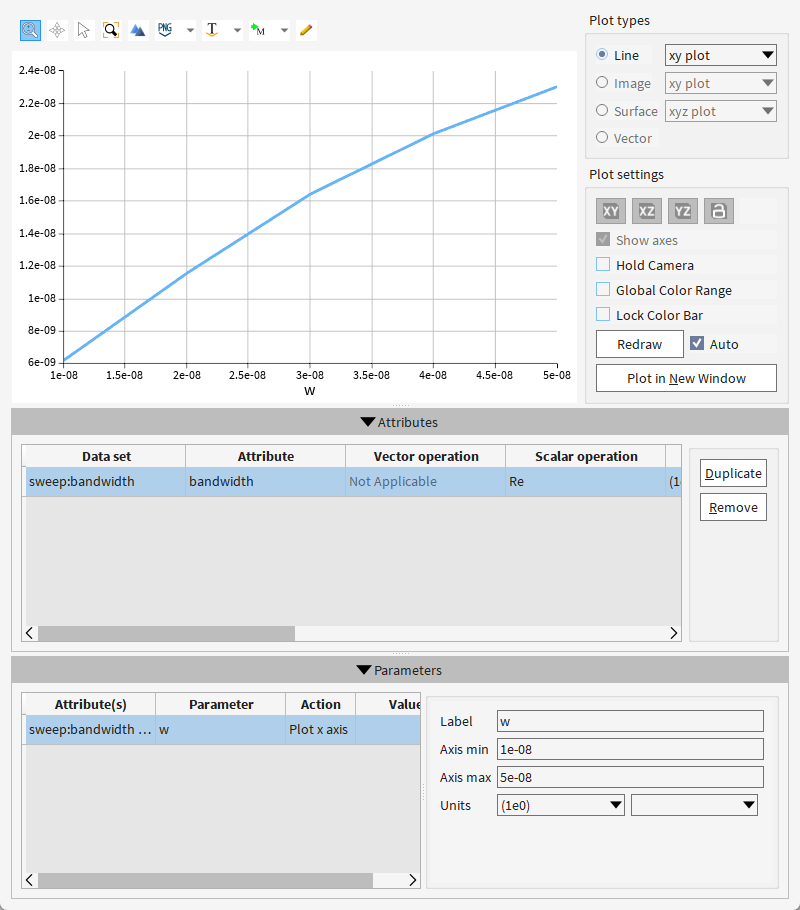
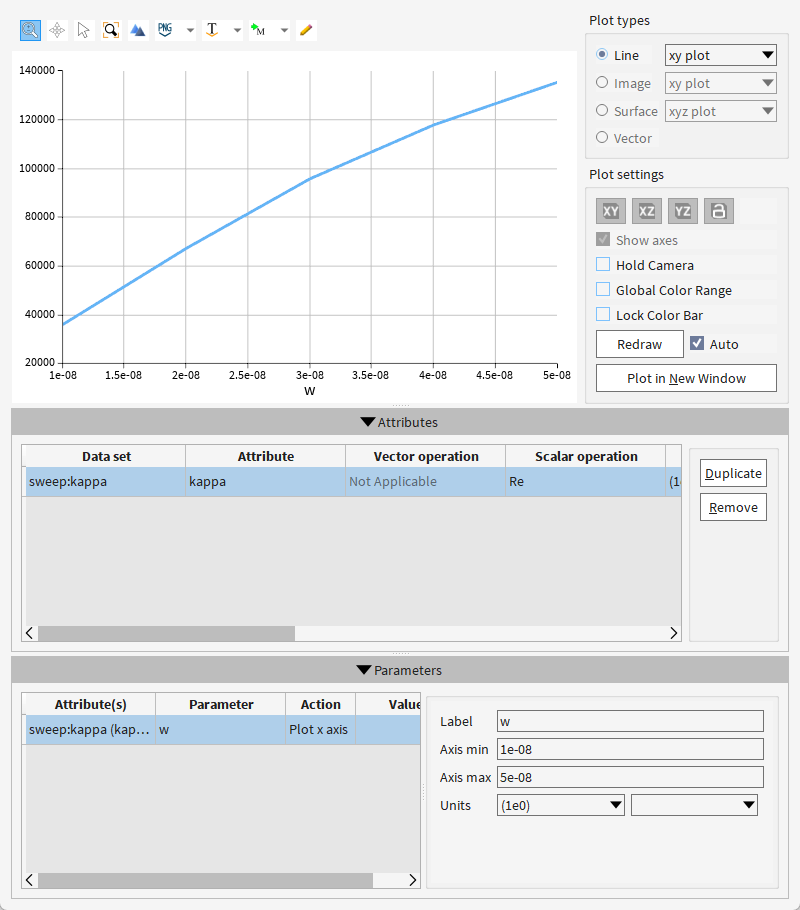
分析:
带宽(bandwidth)与波导宽度(W)的关系
变化趋势:带宽(Δλ)随W增加呈非线性上升,在W<1.5e-8 m时增速显著,W>3e-8 m后趋于平缓(上凸曲线)。
物理机制:
波导宽度增大导致模场约束减弱,光子带隙边缘的群折射率(ng)变化率降低,根据 Δλ∝1/ng,带宽响应逐渐饱和。理论依据:
光子晶体带隙宽度与模式色散的二阶导数相关(∂2ω/∂k2),宽波导中色散曲线平坦化,抑制了带宽的快速增加。
运行结果存疑,官网案例重新下载也是运行有误