(完整代码在底部)
分类阈值选择、分类指标解释、混淆矩阵分析
适用于机器学习模型评估场景,尤其是信用卡欺诈检测这种类别极度不平衡问题。
分类阈值、分类指标与混淆矩阵详解:以信用卡欺诈检测为例
在分类问题中,我们通常关注模型的准确率(accuracy),但在不平衡数据集中,例如信用卡欺诈检测,准确率往往误导性极强。
此时,分类阈值的调节、分类指标的权衡、以及混淆矩阵的分析,才是深入理解模型表现的关键。
本文通过一个实际案例,介绍如何调整分类阈值、如何解读各种指标(Precision、Recall、F1-score)、以及如何利用混淆矩阵评估模型效果。
一、数据准备与模型训练
我们使用 Kaggle 上的著名数据集 creditcard.csv,目标是识别出欺诈交易(Class=1),非欺诈为 Class=0。
样本总数:284,807 条
特征数:30(28个匿名特征 + 金额
Amount+ 时间Time)目标变量:
Class(0=正常交易,1=欺诈交易)

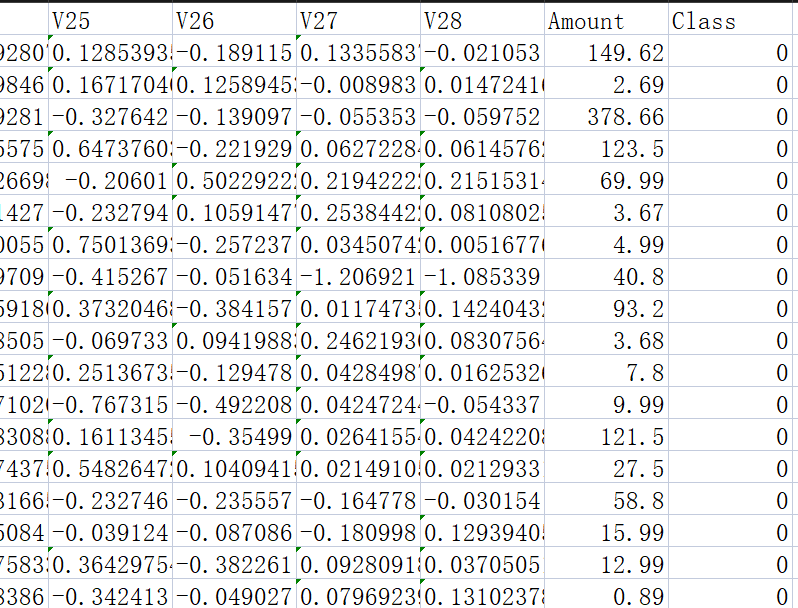
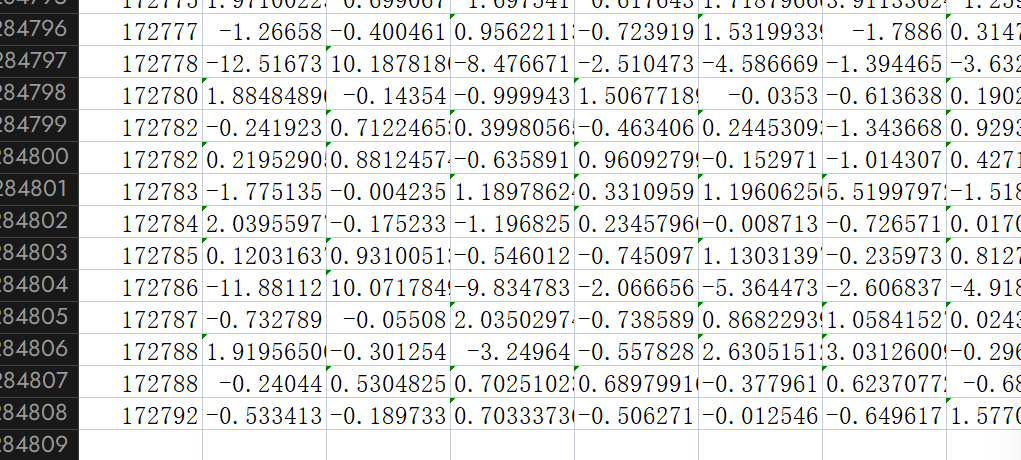
1.1 数据加载与预处理
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression # 导入逻辑回归模型
from sklearn.model_selection import train_test_split, cross_val_score # 用于数据拆分和交叉验证
from sklearn.preprocessing import StandardScaler # 用于数据标准化处理
from sklearn import metrics # 用于模型评估指标计算data = pd.read_csv('creditcard.csv')
# 对交易金额(Amount)进行标准化处理
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
# 准备特征X和标签y
X = data.drop(["Time","Class"], axis=1)
y = data.Class
# 划分训练集与测试集(7:3)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=100)
1.2 模型训练(逻辑回归)
model = LogisticRegression(C=0.01, penalty='l2', solver='lbfgs')
model.fit(X_train, y_train)
# 原混淆矩阵
conf_matrix1 = metrics.confusion_matrix(y_test, model.predict(X_test))
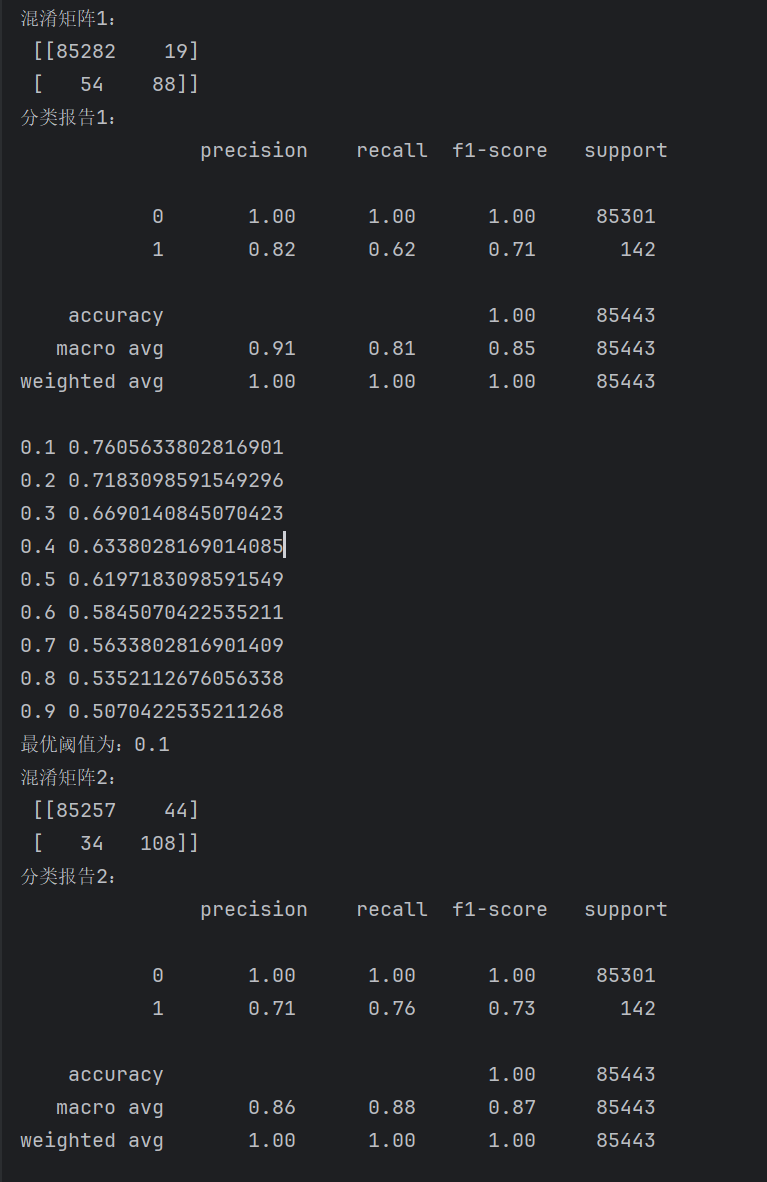
print("混淆矩阵1:\n", conf_matrix1)
# 原阈值预测的分类报告
report1 = metrics.classification_report(y_test, model.predict(X_test))
print("分类报告1:\n", report1)
结果:
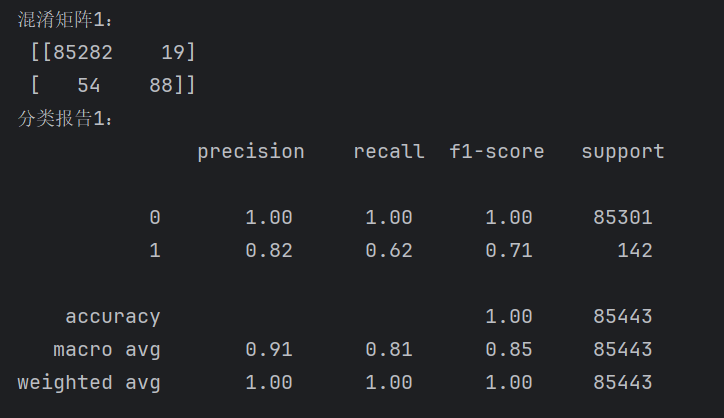
混淆矩阵解释:
| 预测为负类(0) | 预测为正类(1) | |
|---|---|---|
| 真实为负类(0) | True Negative (TN) | False Positive (FP) |
| 真实为正类(1) | False Negative (FN) | True Positive (TP) |
TN(真负):模型正确地识别出非欺诈。
FP(假正):将正常误判为欺诈,可能造成不必要的干预。
FN(假负):模型漏掉了真正的欺诈,严重后果。
TP(真正):模型正确识别欺诈。
| 指标 | 公式 |
|---|---|
| Precision | |
| Recall | |
| F1-score | |
| Accuracy |
二、分类指标解读
在模型训练后,我们获得了一个默认的预测结果(阈值为0.5)。常用的分类指标包括:
| 指标 | 含义 |
|---|---|
| Precision(精确率) | 被预测为正类的条目中 真正是正类的比例。(强调“不误杀”) |
| Recall(召回率) | 实际为正类的条目中 被预测是正类的比例。(强调“不放过”) |
| F1-score | 精确率和召回率的调和平均值,权衡两者。 |
| Support | 每个类别的真实样本数。如85301为测试集(284,807条的30%)中的“0”类 |
⚠️ 注意:在不平衡数据中(如欺诈样本远少于正常样本),accuracy 并不可靠,要重点关注 Recall、F1-score。
三、调整分类阈值:寻找最优 Recall
默认的分类概率阈值是 0.5,即概率大于 0.5 就预测为“欺诈”。然而在欺诈检测中,我们宁愿多抓几个“可疑对象”也不想漏掉真正的欺诈,因此更希望提升召回率(Recall)。
3.1 遍历不同阈值,观察召回率变化
# 以下部分用于寻找最优的分类阈值(默认阈值为0.5)
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9] # 定义要尝试的阈值范围
recalls = [] # 存储不同阈值对应的召回率
for i in thresholds:
y_predict_proba = model.predict_proba(X_test) # 获取模型对测试集的预测概率
y_predict_proba = pd.DataFrame(y_predict_proba) # 将预测概率转换为DataFrame便于处理
y_predict_proba[y_predict_proba[[1]]>i] = 1 # 根据当前阈值调整预测结果:概率大于阈值的视为欺诈(1)
y_predict_proba[y_predict_proba[[1]]<=i] = 0 # 概率小于等于阈值的视为正常(0)
recall = metrics.recall_score(y_test,y_predict_proba[1]) # 计算当前阈值对应的召回率
recalls.append(recall)
print(i,recall)
# 找到最大召回率对应的阈值,作为最优阈值
best_threshold = thresholds[np.argmax(recalls)] # argmax返回数组中最大值所在的索引位置
print(f'最优阈值为:{best_threshold}')3.2 示例输出:
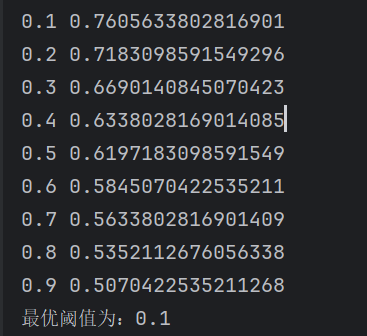
可以看出,在阈值 0.1 时,Recall 达到了最高,意味着我们更不容易漏检欺诈。
但事实上这是不可取的,这种做法是宁杀错不放过
所以实际使用需根据实际需求安排。
下面的部分我们将观察到: “1”的recall的增加, 其实就是牺牲了“0”的recall
四、使用最优阈值预测并绘制混淆矩阵
y_proba = model.predict_proba(X_test)[:, 1] # 只取欺诈类别(label=1)的概率
y_pred_threshold = (y_proba > best_threshold).astype(int)
conf_matrix2 = metrics.confusion_matrix(y_test, y_pred_threshold)
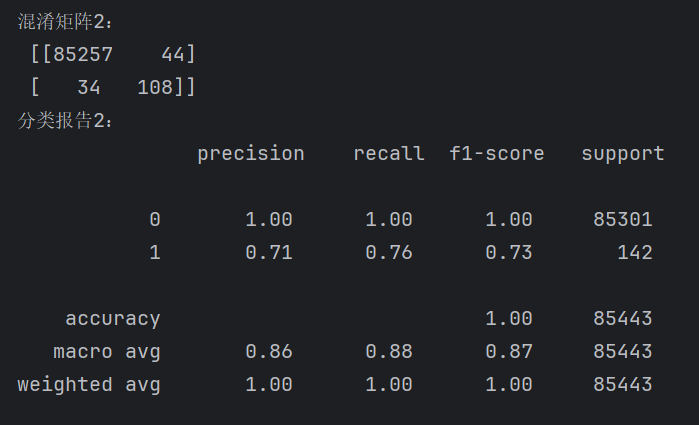
print("混淆矩阵2:\n", conf_matrix2)
report2 = metrics.classification_report(y_test, y_pred_threshold)
print("分类报告2:\n", report2)第一行:
predict_proba(X_test)返回的是每个样本属于每个类别的概率值,格式是形如[P(类0), P(类1)]的二维数组。[:, 1]表示只取每个样本预测为“欺诈类”(类1)的概率。
第二行:
将概率与你前面选出的**最佳阈值(
best_threshold)**进行比较;大于该阈值的,认为是“欺诈”(即类1),否则为“正常”(类0);
用
.astype(int)将布尔值True/False转换成1/0。
五、结语:从“0.5”到“最优阈值”,你学会了吗?
分类问题中,默认的0.5阈值并不是“黄金标准”。针对具体业务目标(是否强调召回率/精确率),我们可以:
自定义分类阈值,寻找最佳的性能平衡点;
深度解读 Precision、Recall、F1-score,避免被“Accuracy”误导;
借助混淆矩阵,全景化理解模型的预测行为;
结合
classification_report快速输出各类指标。
完整代码:
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression # 导入逻辑回归模型
from sklearn.model_selection import train_test_split, cross_val_score # 用于数据拆分和交叉验证
from sklearn.preprocessing import StandardScaler # 用于数据标准化处理
from sklearn import metrics # 用于模型评估指标计算
data = pd.read_csv('creditcard.csv')
# 初始化标准化器,对交易金额(Amount)进行标准化处理
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
# 准备特征数据X(排除时间和目标变量)和目标变量y(欺诈标签,1表示欺诈,0表示正常)
X = data.drop(["Time","Class"], axis=1)
y = data.Class
# 将数据拆分为训练集(70%)和测试集(30%),设置随机种子保证结果可复现
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=100)
# 使用最优惩罚因子训练最终的逻辑回归模型
model = LogisticRegression(C=0.01, penalty='l2', solver='lbfgs')
model.fit(X_train, y_train)
conf_matrix1 = metrics.confusion_matrix(y_test, model.predict(X_test))
report1 = metrics.classification_report(y_test, model.predict(X_test))
print("混淆矩阵1:\n", conf_matrix1)
print("分类报告1:\n", report1)
#----------------------------------------------------------------------------------------
# 以下部分用于寻找最优的分类阈值(默认阈值为0.5)
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9] # 定义要尝试的阈值范围
recalls = [] # 存储不同阈值对应的召回率
for i in thresholds:
y_predict_proba = model.predict_proba(X_test) # 获取模型对测试集的预测概率
y_predict_proba = pd.DataFrame(y_predict_proba) # 将预测概率转换为DataFrame便于处理
y_predict_proba[y_predict_proba[[1]]>i] = 1 # 根据当前阈值调整预测结果:概率大于阈值的视为欺诈(1)
y_predict_proba[y_predict_proba[[1]]<=i] = 0 # 概率小于等于阈值的视为正常(0)
recall = metrics.recall_score(y_test,y_predict_proba[1]) # 计算当前阈值对应的召回率
recalls.append(recall)
print(i,recall)
# 找到最大召回率对应的阈值,作为最优阈值
best_threshold = thresholds[np.argmax(recalls)] # argmax返回数组中最大值所在的索引位置
print(f'最优阈值为:{best_threshold}')
y_proba = model.predict_proba(X_test)[:, 1] # 只取欺诈类别(label=1)的概率
y_pred_threshold = (y_proba > best_threshold).astype(int)
conf_matrix2 = metrics.confusion_matrix(y_test, y_pred_threshold)
report2 = metrics.classification_report(y_test, y_pred_threshold)
print("混淆矩阵2:\n", conf_matrix2)
print("分类报告2:\n", report2)
结果: