01数据结构-最短路径Dijkstra
前言
今天我们主要看一个最短路径算法,迪杰斯特拉算法(Dijkstra Algorithm)。这个算法的主要运用就是计算从某个源点开始到其他顶点的最短路径的算法。
什么是最短路径,什么又是源点,还有最短路径算法有什么用呢?我们来一个一个的看基础概念
1.最短路径Dijkstra
1.1算法场景描述
简单来说,我们要从大兴机场到北京天安⻔,如何规划路线才能换乘最少,并且耗时最少呢?这时候,最短路径算法就派上用场了,你每天使用的导航系统进行道路规划也同样依赖于底层的算法!虽然现实情况可能更复杂一些,但是学习最基础的算法对于我们日后的提升总有莫大的帮助。我们接着看今天的主⻆:迪杰斯特拉算法。
1.2基础概念
什么是源点?
路径起始的第一个顶点称为源点(Source),最后一个顶点称为终点(Destination)。如下图1中,我们用红色标注出的就可以认为是一个路径(V0 ->V1 ->V4 ->V6 ->V8)的源点和终点,但不要有误区,其实图中的任何一个顶点都可作为源点或者终点,源点与终点只是相对一条路径而言的。
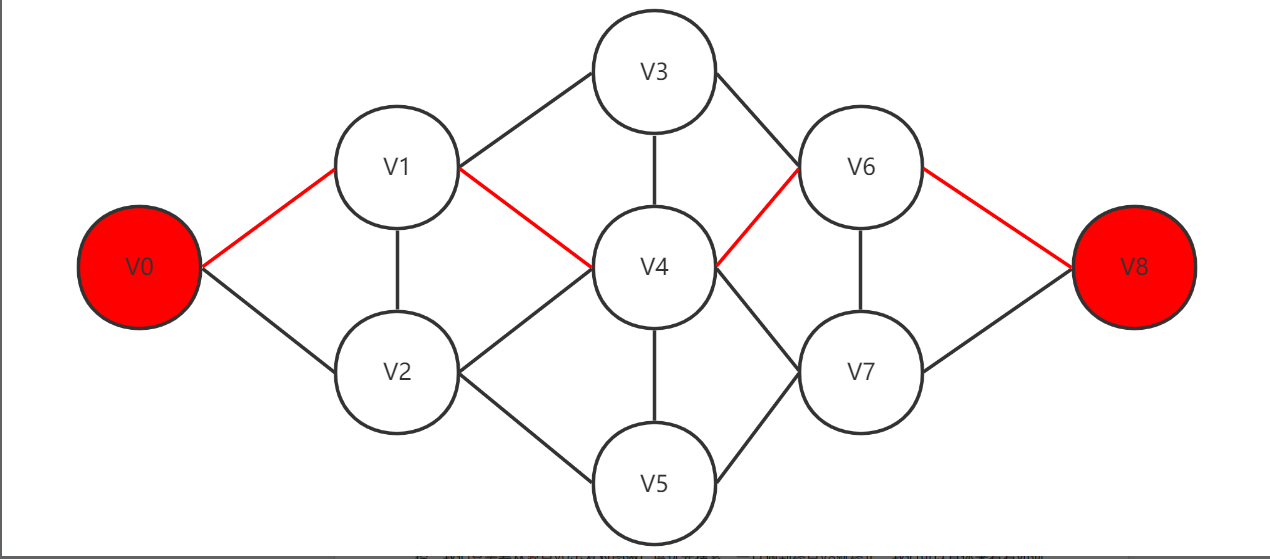
图1
什么是最短路径
对于无向图而言,从源点V0到终点V8的最短路径就是从源点V0到终点V8所包含的边最少的路径。我们只需要从源点V0出发对图做广度优先搜索,一旦遇到终点V8就终止。
1.3Dijkstra概述
Dijkstra算法是荷兰计算机科学家艾兹赫尔·迪杰斯特拉于1956年提出的单源最短路径算法,用于解决带权有向图或无向图中从起点到所有其他节点的最短路径问题,核心思想是贪心策略,逐步扩展最短路径树。注意:仅适用于非负权边的图(负权边会导致算法失效,需用Bellman-Ford算法)我们后面会讲到Bellman-Ford算法。
接下来来感受一下Dijkstra算法:如下图2,假设每个顶点都是石头,石头之间连接着绳子,对应需要多少牛顿的力可以拉起来。此时我们拉A石头,当力来到10N的时候就能提起B,B提起了后意味着力量再提升50N就可以提起C,不断地加力,当力气提到30N的时候可以提起D,D提起了后意味着力量再提升20N就可以提起C,D提起了后意味着力量再提升60N就可以提起C,当力气达到50N的时候,可以通过D提起C,就不需要从B提起C了。关键信息,后拉起来的石头都是先拉起来的石头。从这可以看出和上节课的Prim算法有点像,每激活 一个顶点就会发现新的边,只不过Prim算法是基于激活的顶点选择权值最小的边,DijKstra算法是基于单源点到激活顶点边的权值和的最短距离
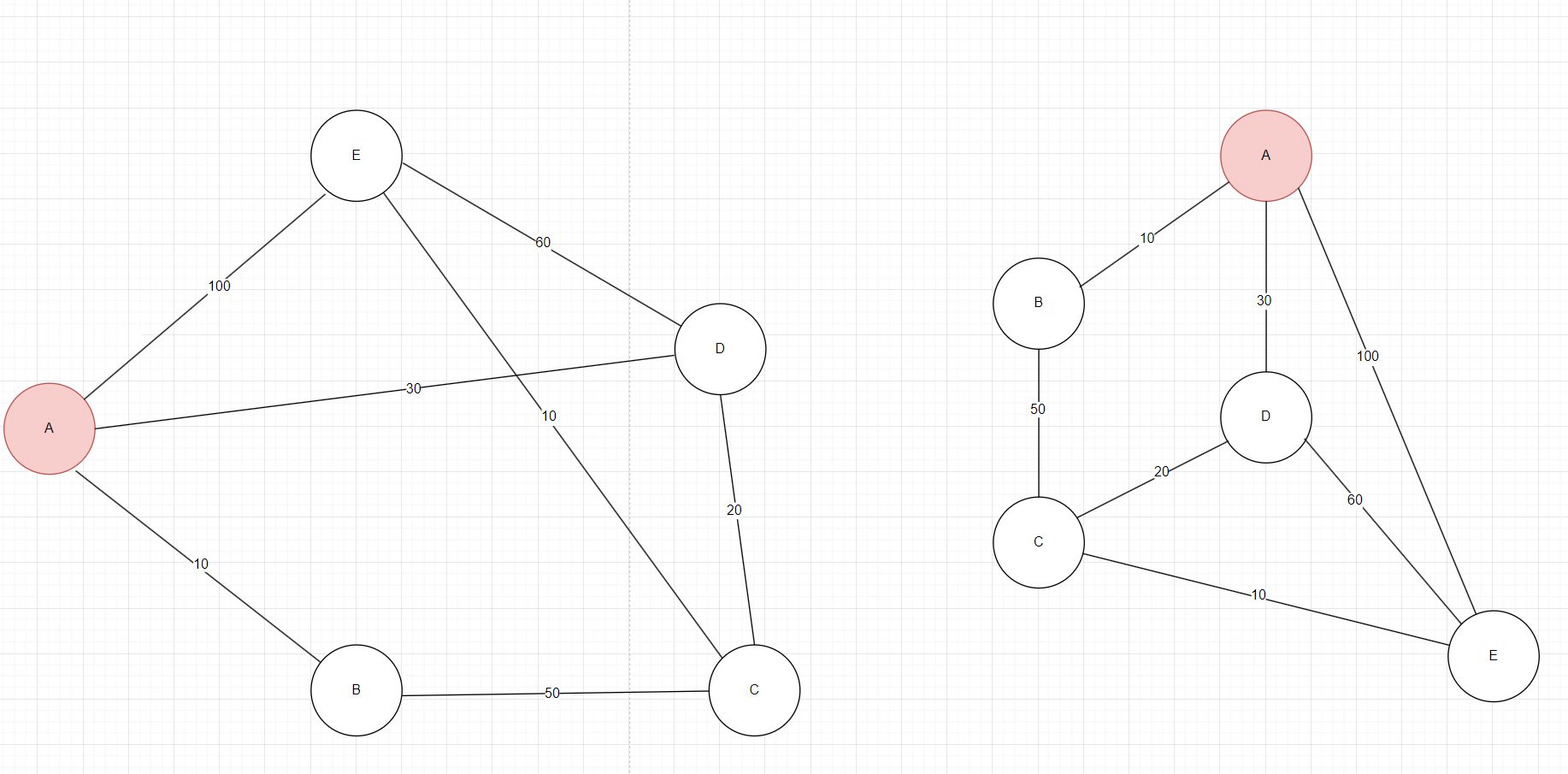
图2
我们需要引入三个辅助数组:dist[],path[],check[]:
- dist描述的是源点到其他节点的距离,初始化时只关心源点到他邻接点的距离
- path描述的是到该顶点前经过哪个顶点到的
- check描述的是该顶点是否被访问。
1.4Dijstra算法模拟
如图3,最开始申请的时候把源点没有到其他距离,就把dist数组里面值设INF(无穷大),把path数组里面的值设为-1,初始化两个数组(把源点的信息加入进去)。
在这里我们把0号顶点当作源点,0号顶点可以到1,2,3号顶点,所以初始化dist数组中的dist[1],dist[2],dist[3]为对应的权值,初始化path[1],path[2],path[3]为源点(因为源点可以到这些顶点)然后选取源点到其他顶点路径权值和最短的那条边并激活对应的顶点,由于初始时只有一条边,所以选取最短的那条也就是权值为4的边。
激活相应的顶点1,注意激活一个顶点,就把顶点对应的check数组更新为已被访问,相应的dist数组也不再更新(即图3中标黄部分,因为已经确定)。激活顶点1后更新dist数组和path数组,更新dist数组的逻辑就是选取源点到其他顶点路径权值和最短的那条边,更新path数组的逻辑就是看谁到哪一个顶点,就在对应的那一个顶点下填谁,此时最短的应该为4+1,所以更新dist[1]为5,更新path[4],path[2](不再是0到2而是1到2),以此重复直到找到最终点(假设这里是6)。
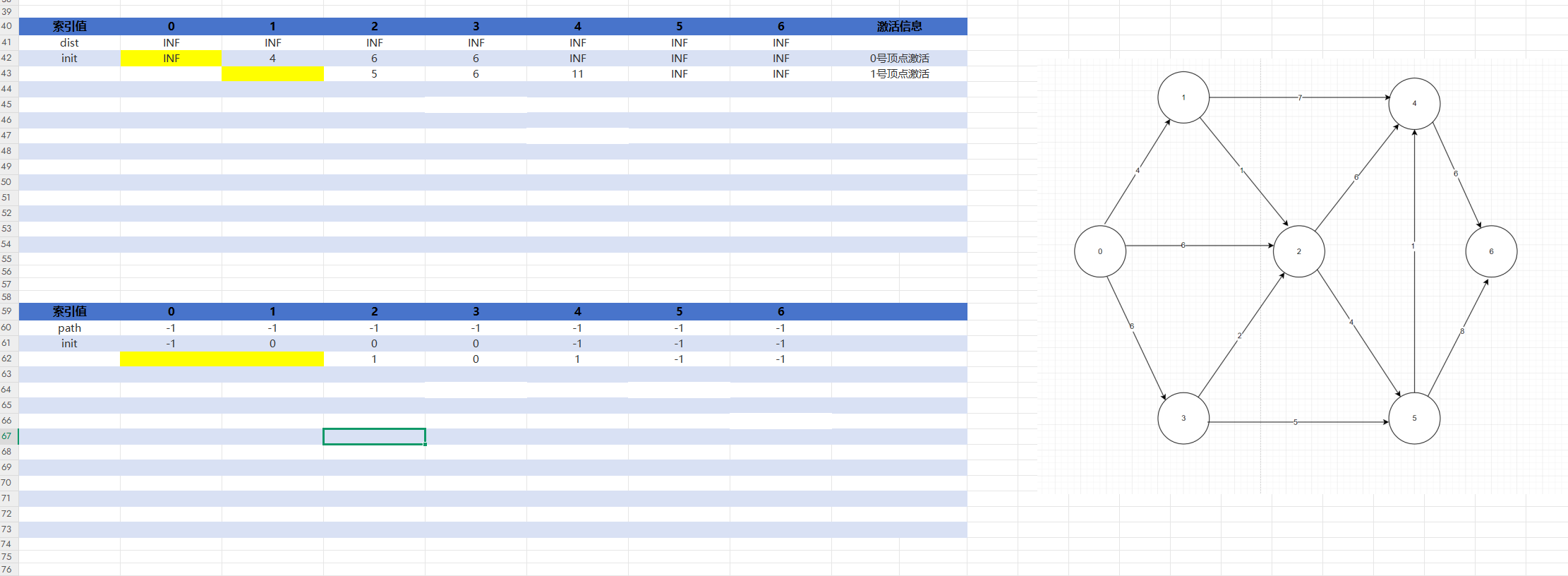
图3
完整过程和结果如图4:要打印出路径只需要创建一个临时栈,压入path[i],然后i=path[i],直到源点,再不断弹栈。
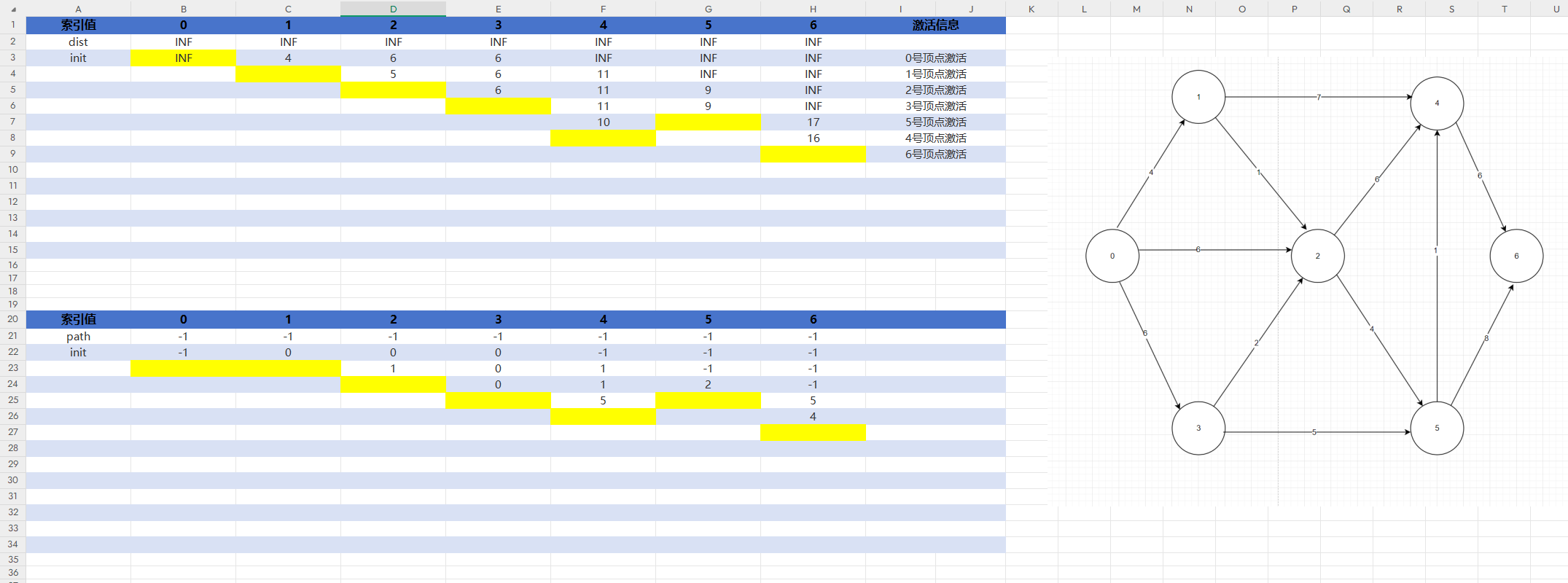
图4
2.最短路径Dijkstra代码实现
接口设计:
#ifndef SHORTPATH_H
#define SHORTPATH_H
#include"matrixGraph.h"
/* Dijkstra算法,以start为源点,dist记录图中每个顶点到单源点的最短路径
* path数组记录每个节点从哪里访问的
*/
void DijkstraMGraph(const MatrixGraph *graph,int start,int dist[],int path[]);
/* 从path信息打印出pos编号的顶点 到 源点的最短路径 */
void showShortPath(const int path[], int num, int pos);
#endif //SHORTPATH_H
Dijkstra核心思想:void DijkstraMGraph(const MatrixGraph *graph,int start,int dist[],int path[]);
void DijkstraMGraph(const MatrixGraph *graph, int start, int dist[], int path[]) {
int *mark; // 节点的访问记录
mark = malloc(graph->nodeNum * sizeof(int));
// 1. 激活start后,节点距离表dist更新,path数组的初始化,根节点对应-1
for (int i = 0; i < graph->nodeNum; ++i) {
dist[i] = graph->edges[start][i];
mark[i] = 0;
if (dist[i] < INF) {
path[i] = start;
} else {
path[i] = -1;
}
}
mark[start] = 1;
path[start] = -1;
dist[start] = 0;
int k;
// 2. 从dist里找最小值
for (int i = 0; i < graph->nodeNum-1; ++i) {
int min = INF;
k = 0;
// 从未激活的节点中,找到一个源点的最短路径(拿到dist数组中最小的值和索引)
for (int j = 0; j < graph->nodeNum; ++j) {
if (mark[j] == 0 && dist[j] < min) {
min = dist[j];
k = j;
}
}
mark[k]=1;
// 以刚激活的节点,更新源点到其他节点路径
for (int j = 0; j < graph->nodeNum; ++j) {
if (mark[j] == 0 && dist[j]>graph->edges[k][j]+dist[k]) {
dist[j] = dist[k] + graph->edges[k][j];
path[j] = k;
}
}
}
free(mark);
}
我把上节课的Prim算法的核心也粘贴在这里,大家可以对比一下和上节课的Prim算法的不同之处
Prim算法核心:int PrimMGraph(const MatrixGraph* graph, int startV, EdgeSet* result);
int PrimMGraph(const MatrixGraph* graph, int startV, EdgeSet* result) {
int *cost = malloc(sizeof(int) * graph->nodeNum); // 图中各顶点的权值数组
int *mark = malloc(sizeof(int) * graph->nodeNum); // 图中顶点激活的状态
int *visited = malloc(sizeof(int) * graph->nodeNum); // 从哪个顶点开始访问,-1表示没有被访问到
int sum = 0;
// 1. 更新第一个节点激活的状态
for (int i = 0; i < graph->nodeNum; i++) {
cost[i] = graph->edges[startV][i];
mark[i] = 0;
// 1.1 更新visit信息,从哪个节点可以访问
if (cost[i] < INF) {
visited[i] = startV;
} else {
visited[i] = -1;
}
}
mark[startV] = 1;
int k = 0;
// 2. 动态激活节点,找最小值
for (int i = 0; i < graph->nodeNum - 1; ++i) {
int min = INF;
k = 0;
for (int j = 0; j < graph->nodeNum; ++j) {
if (mark[j] == 0 && cost[j] < min) {
min = cost[j];
k = j;
}
}
mark[k] = 1;
result[i].begin = visited[k];
result[i].end = k;
result[i].weight = min;
sum += min;
// 每激活一个顶点,需要更新cost数组
for (int j = 0; j < graph->nodeNum; ++j) {
if (mark[j] == 0 && graph->edges[k][j] < cost[j]) {
cost[j] = graph->edges[k][j];
visited[j] = k;
}
}
}
free(cost);
free(mark);
free(visited);
return sum;
}
大框架都是相同的,先申请数组空间,再初始化,开始循环处理逻辑,处理的逻辑是先在一个权值数组里找到最小的权值,激活对应的顶点,然后更新权值数组,只是更新的方式不同,Prim算法中是基于激活的顶点更新权值数组,而Dijkstra是站在源点看路径的权值和,更新权值数组里面的值。Prim是单个边的权值,Dijkstra是路径和的权值。
打印路径:void showShortPath(const int path[], int num, int pos)
void showShortPath(const int path[], int num, int pos) {
//在栈上申请栈空间
int data[num];
int lastPos=0;
//压栈
while (path[pos] != -1) {
data[lastPos]=pos;
++lastPos;
pos = path[pos];
}
//把0压进去
data[lastPos]=0;
//弹栈
while (lastPos!=-1) {
printf("%d\t",data[lastPos]);
--lastPos;
}
printf("\n");
}
因为直接打印的话,打印出的会是倒序,所以想到栈的先入后出的特点。
最后来测一下:
#include <stdio.h>
#include <stdlib.h>
#include "DijkstraShortPath.h"
void setupMGraph(MatrixGraph *graph) {
char *names[] = {"0", "1", "2", "3", "4", "5", "6"};
initMatrixGraph(graph, names, sizeof(names) / sizeof(names[0]), 1, INF);
addMGraphEdge(graph, 0, 1, 4);
addMGraphEdge(graph, 0, 2, 6);
addMGraphEdge(graph, 0, 3, 6);
addMGraphEdge(graph, 1, 4, 7);
addMGraphEdge(graph, 1, 2, 1);
addMGraphEdge(graph, 2, 4, 6);
addMGraphEdge(graph, 2, 5, 4);
addMGraphEdge(graph, 3, 2, 2);
addMGraphEdge(graph, 3, 5, 5);
addMGraphEdge(graph, 4, 6, 6);
addMGraphEdge(graph, 5, 4, 1);
addMGraphEdge(graph, 5, 6, 8);
}
int main() {
MatrixGraph graph;
setupMGraph(&graph);
int *dist = malloc(sizeof(int) * graph.nodeNum);
int *path = malloc(sizeof(int) * graph.nodeNum);
DijkstraMGraph(&graph, 0, dist, path);
printf("to 6 node: ");
showShortPath(path, graph.nodeNum, 6);
printf("to 3 node: ");
showShortPath(path, graph.nodeNum, 3);
free(dist);
free(path);
}
结果:
D:\work\DataStruct\cmake-build-debug\03_GraphStruct\DijkstraPath.exe
to 6 node: 0 1 2 5 4 6
to 3 node: 0 3
进程已结束,退出代码为 0
大概先写这些吧,今天的博客就先写到这,谢谢您的观看。