替换数字（字符串算法）

替换数字

卡码网题目链接(opens new window)

给定一个字符串 s，它包含小写字母和数字字符，请编写一个函数，将字符串中的字母字符保持不变，而将每个数字字符替换为number。

例如，对于输入字符串 "a1b2c3"，函数应该将其转换为 "anumberbnumbercnumber"。

对于输入字符串 "a5b"，函数应该将其转换为 "anumberb"

输入：一个字符串 s,s 仅包含小写字母和数字字符。

输出：打印一个新的字符串，其中每个数字字符都被替换为了number

样例输入：a1b2c3

样例输出：anumberbnumbercnumber

数据范围：1 <= s.length < 10000。

思路

如果想把这道题目做到极致，就不要只用额外的辅助空间了！ （不过使用Java和Python刷题的录友，一定要使用辅助空间，因为Java和Python里的string不能修改）

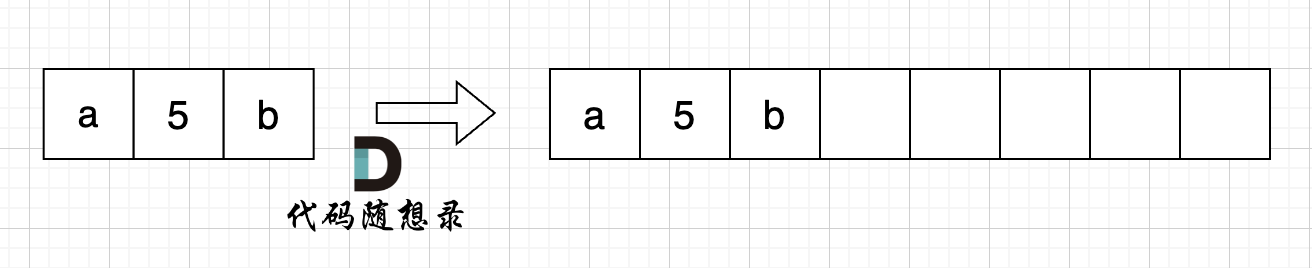
首先扩充数组到每个数字字符替换成 "number" 之后的大小。

例如 字符串 "a5b" 的长度为3，那么 将 数字字符变成字符串 "number" 之后的字符串为 "anumberb" 长度为 8。

如图：

然后从后向前替换数字字符，也就是双指针法，过程如下：i指向新长度的末尾，j指向旧长度的末尾。

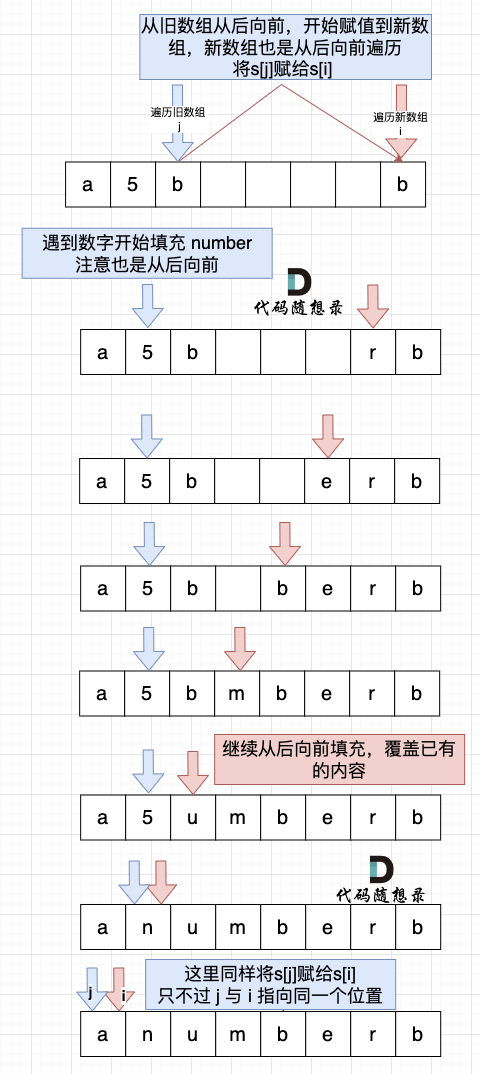
有同学问了，为什么要从后向前填充，从前向后填充不行么？

从前向后填充就是O(n^2)的算法了，因为每次添加元素都要将添加元素之后的所有元素整体向后移动。

其实很多数组填充类的问题，其做法都是先预先给数组扩容带填充后的大小，然后在从后向前进行操作。

这么做有两个好处：

1. 不用申请新数组。
2. 从后向前填充元素，避免了从前向后填充元素时，每次添加元素都要将添加元素之后的所有元素向后移动的问题。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String s = sc.next();
        
        // 记录原始长度
        int originalLen = s.length();
        int newLen = originalLen;
        
        // 计算扩展后的总长度：每个数字替换为 "number"（多5个字符）
        for (int i = 0; i < originalLen; i++) {
            if (s.charAt(i) >= '0' && s.charAt(i) <= '9') {
                newLen += 5;
            }
        }
        
        // 创建结果字符数组
        char[] ret = new char[newLen];
        
        // 先将原字符串复制到结果数组前部
        for (int i = 0; i < originalLen; i++) {
            ret[i] = s.charAt(i);
        }
        
        // 从后往前处理：避免覆盖，实现原地扩展
        for (int i = originalLen - 1, j = newLen - 1; i >= 0; i--) {
            if (ret[i] >= '0' && ret[i] <= '9') {
                // 倒序填入 "number"
                ret[j--] = 'r';
                ret[j--] = 'e';
                ret[j--] = 'b';
                ret[j--] = 'm';
                ret[j--] = 'u';
                ret[j--] = 'n';
            } else {
                ret[j--] = ret[i];
            }
        }
        
        // 输出结果
        System.out.println(ret);
    }
}

一、时间复杂度：O(n)

其中 n 是输入字符串的原始长度。

分析：

步骤	时间复杂度	说明
第一次遍历（计算长度）	O(n)	遍历原字符串每个字符一次
复制原字符串到数组	O(n)	再次遍历原字符串
从后往前填充数组	O(m)	m 是最终数组长度，最坏情况是全是数字，m ≈ 6n → 仍是 O(n)

✅ 所有循环都是线性的，且最多遍历原字符串 2 次 + 结果数组 1 次。

虽然结果数组长度可能达到 6n，但它是输入长度的常数倍，所以：

总时间复杂度 = O(n + n + 6n) = O(n)

---

📊 二、空间复杂度：O(n)

其中 n 是输入字符串的原始长度。

分析：

空间占用项	大小	是否计入
char[] ret 数组	newLen ≈ 最多 6n	✅ 是主要空间开销
String s	n	✅ 输入本身，但通常不计入额外空间
其他变量（i, j, len 等）	O(1)	忽略

✅ 虽然 ret 数组最大可达 6n，但它是输入长度的 常数倍，所以：

空间复杂度 = O(n)

我看ai说可以改为这样（似乎确实比较可以）

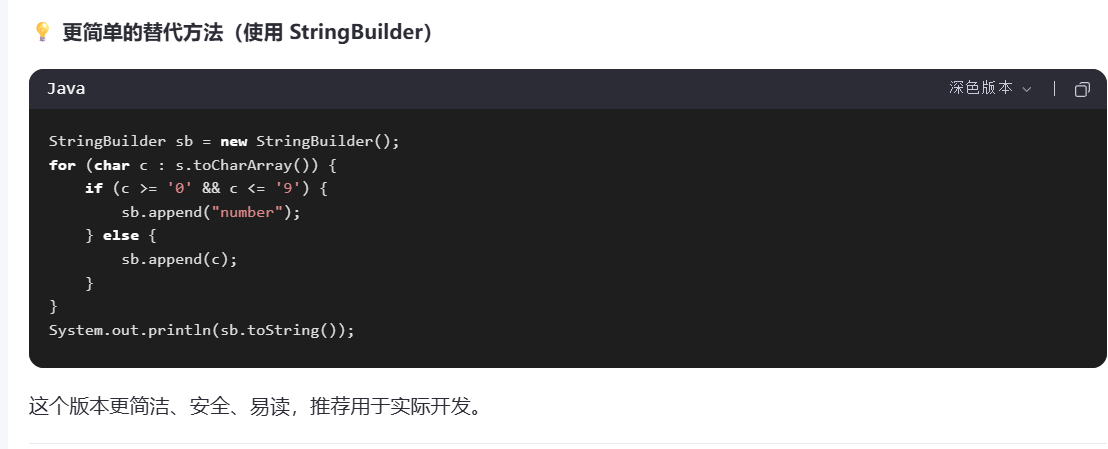
换成这个后：

📊 一、时间复杂度：O(n)

其中 n 是输入字符串的原始长度。

分析：

步骤	时间消耗
s.toCharArray()	O(n) —— 创建一个长度为 n 的字符数组
for-each 循环	O(n) —— 遍历每个字符一次
sb.append("number")	每次调用是 O(6) = O(1)（常数时间）
sb.append(c)	O(1)
sb.toString()	O(m) —— m 是结果字符串总长度，最坏约 6n

总时间：

• 循环执行 n 次
• 每次操作是 O(1)（无论是 append 字符还是字符串）
• 最后生成字符串是 O(m) ≈ O(6n) = O(n)

✅ 所以：

总时间复杂度 = O(n)

⚠️ 注意：虽然 append("number") 看似“操作6个字符”，但它内部是批量写入，时间是常数（与输入长度 n 无关），所以仍是 O(1) 操作。

---

📊 二、空间复杂度：O(n)

其中 n 是输入字符串的原始长度。

分析：

空间占用项	大小	是否计入
s.toCharArray()	O(n)	✅ 创建了新的 char[] 数组
StringBuilder 内部缓冲区	O(m) ≈ O(6n)	✅ 存储最终结果
最终 toString() 生成的字符串	O(m) ≈ O(6n)	✅ 输出字符串

关键点：

• toCharArray() 会复制整个字符串 → 额外 O(n) 空间
• StringBuilder 至少需要 O(m) ≈ O(n) 空间存储结果
• 结果字符串最多是原长度的 6 倍（全是数字时）

✅ 所以：

总空间复杂度 = O(n + 6n) = O(n)

💡 虽然实际用了更多内存，但它是输入长度的常数倍，所以仍为 O(n)